水下上弧形板结构的水动力特性研究

王 科，施鹏飞，陈彧超，边 疆，信 晗，程小明

（1.大连理工大学 工业装备与结构分析国家重点实验室，工程力学系，辽宁 大连 116024；2.中国船舶科学研究中心，江苏 无锡 214082）

水下上弧形板结构的水动力特性研究

王 科1，施鹏飞1，陈彧超1，边 疆1，信 晗1，程小明2

（1.大连理工大学 工业装备与结构分析国家重点实验室，工程力学系，辽宁 大连 116024；2.中国船舶科学研究中心，江苏 无锡 214082）

文章应用边界单元法，依据波浪绕射和辐射理论研究了一种新型的板式防波堤结构—上弧形板结构。研究中通过与另外三种板式防波堤结构(下弧形板结构，单板结构，双层板结构)的对比，验证了这一新型结构具有更好的消波效果。文中重点分析了这种新型结构的散射波浪力、透射系数和反射系数，并且为了进一步揭示这种结构的消波原理，对该结构周围的流场进了分析。研究发现：（1）上弧形板结构在横荡方向上所受波浪力最小。（2）当潜深波高比为0.05时，该结构的消波效果比其他三种结构增强约50%。（3）通过对上弧形板结构的速度流场分析，发现上弧形板结构上部有明显回流。

上弧形板结构；边界单元法；透射系数；速度流场分析

0 引 言

随着海洋工程向深海的发展，海洋平台建设的大型化和海洋开发的复杂化已经成为一种趋势。这就对防波堤的建设提出了更高的要求。传统的水工结构已经不适应深海发展的需要，板式防波堤作为一种新型防波堤结构，由于其具有造价低、施工便捷、受水深和地质条件影响小等特点备受海洋工程领域的广泛关注。而在对板式防波堤的分析过程中，透射系数和反射系数是非常重要的，直接反映了防波堤的消波效果，速度流场的分布则揭示了防波堤的消波机理。

然而，现在的板式防波堤一般有单板式、双板式或者平板—浮箱式等等。单板式防波堤造价低、便于安装，但是防波效果不如后者；双板式或者平板—浮箱式防波堤具有良好的防波效果，但是相比于单板式防波堤来说造价高。本文提出了一种新型的上弧板式结构，其能同时兼有单板和双板结构的优点。

对于单层平板式防波堤，前人已经做了大量的数学推导和实验工作[1-4]。早在1957年，Stoker[5]就提出了一个在长波作用下的水下固定浮板的反射系数和透射系数的分析方法；Ursell等学者[6-9]对波浪与单一平板之间相互作用下的透射系数与反射系数结果做了充分的研究；邱大洪[10]提出了一种单一薄板结构形式的防波堤，基于波能流理论，推导出了透射系数及反射系数在任意水深条件下的解析表达式；Wang Ke等[11]应用格林函数方法研究了水平及垂直单板的反射系数及透射系数，讨论了相对板长和板间距的变化对板式防波堤消波性能的影响；Burk[12]采用Wiener-Hopf方法分析解决了水下平板在深水下的波浪散射问题；Siew和Hurley[13]采用匹配渐进展开的方法解决了水下平板在浅水下的波浪流动问题。

对于多层平板式和平板—浮箱式防波堤，Wang[14]通过实验研究了多层板式防波堤的消波性能；Usha和Gayathr[15]从线性势波理论出发，利用匹配特征函数法研究了在二维情况下，双层水平板型防波堤的波浪透射和反射问题。Wang和Shen[16]利用匹配特征函数法研究了多层潜式水平板对波浪的透射和反射问题。王永学等[17]通过模型试验的方法研究了导桩锚固平板—浮箱结构的消波性能及运动响应。

本文依据有限水深条件下波浪的绕射、辐射理论，发展了能求解任意复杂形状板式结构的边界单元算法。通过水下单板、双板、上弧形板及下弧形板等四种结构透射系数和反射系数的比较，获得水动力特性较好的上弧形板式结构新形式；同时，研究了上弧形板式结构附近速度流场的分布情况。

1 数学模型与理论方法

1.1 计算模型

有限水深条件下波浪与水下单板、双板、上弧形板及下弧形板等四种结构相互作用的计算示意图如图1所示，图中水深为H，平板上边缘和弧形板两端的上边缘距自由水面HS，板的厚度为PT，板长为B=2a。二维笛卡尔坐标系oxy选取在水面中心处，入射波沿+x方向传播。

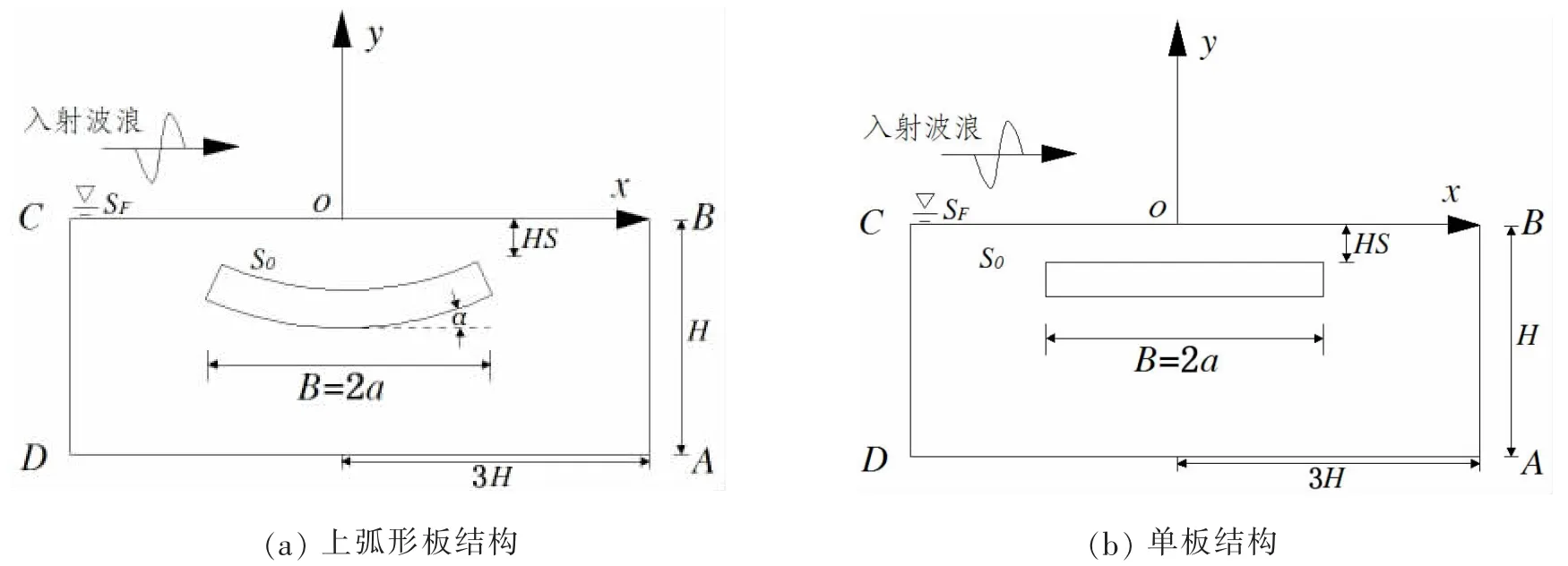
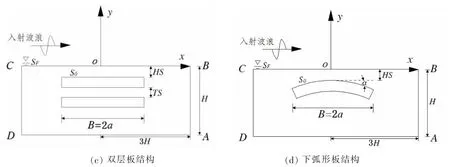
图1 不同板结构计算示意图Fig.1 Sketch of different breakwater

2 边界积分方程的数值离散

2.1 线性单元及方程离散

假设速度势在每一个单元上都呈线性分布。采用等参单元，单元上的变量和坐标可表示如下：

2.2 流场速度计算公式

当流体域内的网格为四节点四边形单元时，则流体域内各物理量可表示为：

其中：［J］为雅可比行列式。

3 结果与分析

3.1 计算区域划分及算例验证

对于如图1所示的有限水深波浪数值水槽，水平长度取为水深的6倍，坐标原点位于自由水面中心处。经过试算，计算区域网格各边的剖分为：（1）流域边界上：波浪入射边界和流出边界各划分60个单元，自由表面划分360个单元；（2）上弧形板结构：上下边各划分80个单元，弧形结构端部各划分40个单元；（3）单板结构：整体划分180个单元；（4）双板结构：每个单板结构都划分180个单元。

为保证计算结果的准确性，在波浪数值水槽不同边界的交界处采用双重节点布置，在板式防波堤的端部直角几何奇异点处也采用双重节点布置，这类双重节点具有相同的位置坐标和速度势，但位于不同的边界单元上，法线导数也不同。图2为本文与Hsu等[18]文中透射系数结果的对比，可以发现二者吻合良好，证明本研究的方法是有效的。

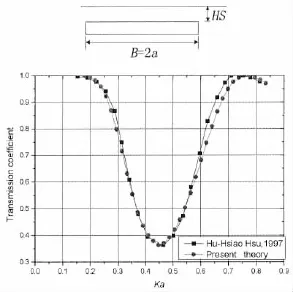
图2 本文与Hsu等[18]文中透射系数结果对比(H=1.0 m，HS=0.2 m，TT=0.04 m，B=2.0 m)Fig.2 Comparison of transmission coefficient with Hsu et al

3.2 波浪力分析

图3为不同板式结构所受波浪力在垂荡、横荡及横摇方向的计算结果，横坐标KB/2表示无因次化的相对板长，纵坐标为无因次化波浪力。由图可见，三个方向上不同结构所受波浪力的趋势基本相同，垂荡方向上的波浪力明显比横荡、横摇方向上的大。在垂荡方向上，四种结构的波浪力曲线都是随着KB/2的增大，呈现先增大后减小的趋势，其中当0.2＜KB/2＜0.8时，上弧形板结构所受到的波浪力较大；在其余波浪频率，四种结构所受到的波浪力相差不大，并且四种结构都在KB/2=0.4处取得极大值；在横荡方向，KB/2＜0.6时，板结构波浪力随波浪频率的增加而增加，双层板结构所受波浪力最大，下弧形板次之，单板和上弧形板波浪力最小，并且数值几乎相同。KB/2＞0.6时，四种板结构的波浪力随波浪频率的增加而减小，由于上弧形板上部水体反复震荡，板上下水体速度产生相位差，使得上弧形板结构在横荡方向的波浪力急速衰减，比单板要小得多，而且在KB/2=1.8处波浪力为零；在横摇方向上，单板波浪力最小，上弧形板结构次之。当0＜KB/2＜0.9时，双层板结构受到的波浪力最大。当0.9＜KB/2＜2.0时，下弧形板结构所受的波浪力最大，并且在KB/2=1.1处取得极大值。

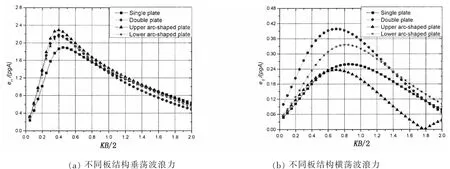
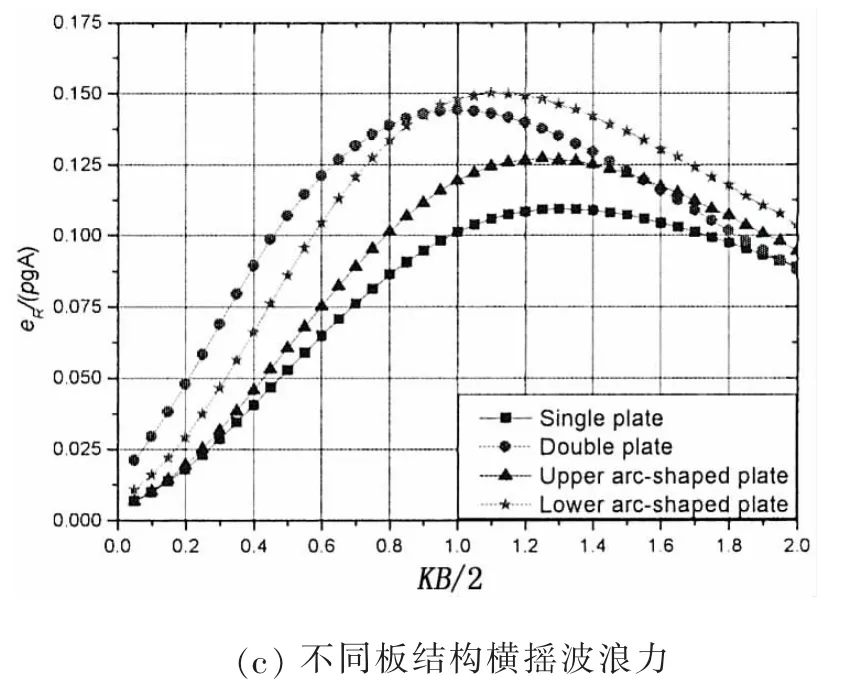
图3 不同板式结构的波浪力（H=1.5 m，HS=0.1 m，TT=0.05 m，TS=0.1 m，α=5°）Fig.3 Wave exciting force of different plate breakwater

4.3 透射系数与反射系数分析

图4为不同板式防波堤结构的透射系数和反射系数计算结果。随着KB/2的增加，透射系数（图4（a））呈先减小后增大的抛物线形变化，而反射系数则是随着KB/2的增加先增加后减小（图4（b））。从图3（a）中可以发现，在整个波浪频率内，上弧形板结构的透射系数远好于其他三种结构，尤其是在0.4＜KB/2＜0.8区域内，当KB/2=0.55时，波浪透射系数由0.78减小为0.68，消波效果增加约15%。

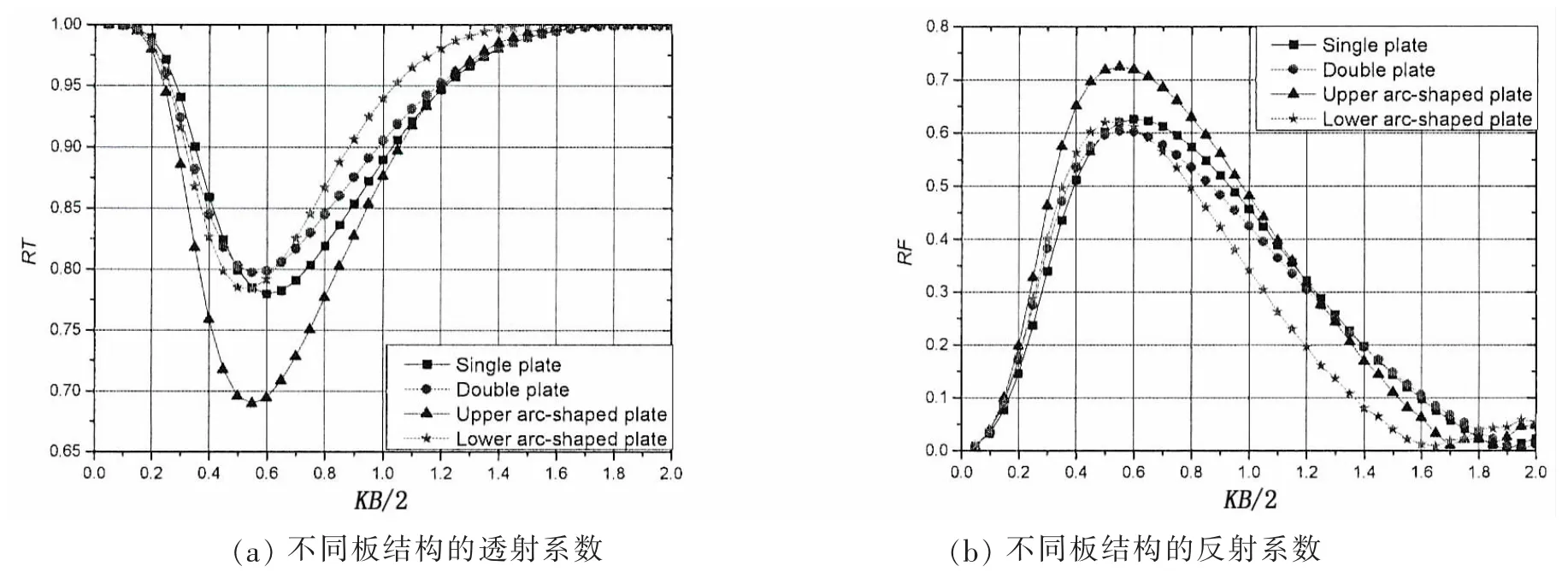
图4 不同板结构的透射系数和反射系数（H=1.5 m，HS=0.1 m，TT=0.05 m，TS=0.1 m，α=5°）Fig.4 Transmission coefficient and reflection coefficient of different plate breakwater

图5 不同板结构的透射系数和反射系数（H=1.5 m，HS=0.1 m，TT=0.05 m，TS=0.1 m，α=5°）Fig.5 Transmission and reflection coefficient of different plate breakwater

图5为潜深变为HS=0.05 m时，不同板结构的透射系数和反射系数计算结果。此时，上弧形板结构的消波效果仍然是最好的。当KB/2=0.5时，透射系数可以由单板的30%减小为15%，消波效果增加约50%。

3.4 速度流场分析

为进一步揭示上弧形板结构的消波原理，本文以KB/2=0.6时为例，对其流场进行分析，研究在整个消波过程中水质点的速度变化。由于在板附近流域速度变化比较明显，所以分析区域限定为板周围长*宽=1.2 m×0.6 m的范围。

图6表示图3（a）中KB/2=0.6时的水下上弧形板结构的速度流场图。由透射结果可知，此时的上弧形板结构消波效果最好。在横荡运动时，弧形板下部的速度大于上部，在弧形板的外部端点处速度较大；由于板结构的几何对称和横荡运动的反对称特性，横荡流场也是反对称的。在垂荡运动时，上弧形板结构周围的水质点在y方向往复运动，在板两侧速度较小，板上下部分的速度较大并且幅值几乎相等。由于上弧板弯曲角度不大，板上下表面流体以垂向运动为主，横向速度很小；在横摇运动时，上弧形板结构的上部水质点有回流，并且板前后端部流场变化剧烈，这是上弧形板这一特殊形状造成的。从图6（d）和图6（e）中可以看到，散射速度场和总速度流场几乎相同，说明在上弧形板结构的消波过程中起重要作用的是散射模态，这也验证了用频域散射速度势计算波浪透反射系数的科学性。

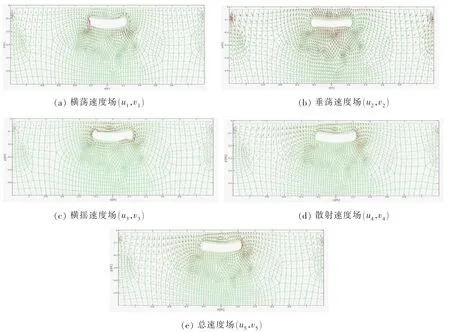
图6 上弧形板结构速度流场图（KB/2=0.6，H=1.5 m，HS=0.1 m，TT=0.05 m，TS=0.1 m，α=5°）Fig.6 Fluid velocity field for upper arc-shaped plate breakwater

4 结 论

本文应用边界单元方法对单板、双层板、下弧形板及上弧形板结构的波浪力和透反射系数和速度流场进行了数学模型研究，研究发现由于上弧形板结构的特殊形状，垂荡方向波浪力最大，但由于板上部的浅水回流，使得横荡波浪力比单板结构还要小，特别是在KB/2＜0.6。通过透射系数和反射系数的分析，上弧形板结构的消波效果明显比其他三种结构要好。当KB/2=0.6，HS=0.05时，上弧形板结构的透射系数能达到0.15。

[1]侯 勇,王永学,高 军.新型浮式防波堤水动力特性试验研究[J].水运工程,2010(2)：50-53. Hou Yong,Wang Yongxue,Gao Jun.Experiments on hydrodynamic performance of new floating breakwater[J].Port& Waterway Engineering,2010(2)：50-53.

[2]王 科.潜式水平板型防波堤消波效果研究[D].大连：大连理工大学,2001. Wang Ke.Study on submerged horizontal plate type breakwater[D].Dalian：Dalian University of Technology,2001.

[3]Parsons N F,Martin P A.Scattering of water waves by submerged plates using hypersingular integral equations[J].Applied Ocean Research,1992,14(5)：313-321.

[4]Roy P D,Ghosh S.Wave force on vertically submerged circular thin platein shallow water[J].Ocean Engineering,2006, 33(14)：1935-1953.

[5]Stoker J J.Water waves[M].New York：Interscience Publishers,1957.

[6]Ursell F.The effect of a fixed vertical barrier on surface waves in deep water[J].Proc.Camb.Phil.Soc.,1947,43(3)：374-382.

[7]Albert E H.Water waves over a channel of finite depth with a submerged plane barrier[J].Canadian Journal of Mathematics,1950,2(2)：210.

[8]Kanayama K,Fujiwara T.Transmission of wave past a rigid vertical thin barrier[J].Technology Reports of the Yamaguchi University,1976,1(4)：427-438.

[9]Kriebel D L,Bollmann C A.Wave transmission past vertical wave barriers[J].Coastal Engineering Proceedings,1996,1 (25)：2470-2483.

[10]邱大洪,王学庚.深水薄板式防波堤的理论分析[J].水运工程,1986(4)：8-12. Qiu Dahong,Wang Xuegeng.Theoretical study of thin plate type breakwater in deep water[J].Port&Waterway Engineering,1986(4)：8-12.

[11]Wang Ke,Zhang Zhiqiang,Xu Wang.Transmitted and reflected coefficients for horizontal or vertical plate type breakwater[J].China Ocean Engineering,2011,25(2)：285-294.

[12]Burke J E.Scattering of surface waves on an infinitely deep fluid[J].Journal of Mathem atical Physics,2004,5(6)：805-819.

[13]Siew P F,Hurley D G.Long surface waves incident on a sub-merged horizontal plate[J].Journal of Fluid Mechanics, 1977,83(01)：141-151.

[14]Wang Y,Wang G,Li G.Experimental study on the performance of the multiple-layer breakwater[J].Ocean Engineering, 2006,33(13)：1829-1839.

[15]Usha R,Gayathri T.Wave motion over a twin-plate breakwater[J].Ocean Engineering,2005,32(8)：1054-1072.

[16]Wang K H,Shen Q.Wave motion over a group of submerged horizontal plates[J].International Journal of Engineering Science,1999,37(6)：703-715.

[17]王永学,董华洋,刘 冲.实验研究固桩浮箱—平板结构[J].中国海洋工程：英文版,2010,24(1)：183-190. Wang Yongxue,Dong Huayang,Liu Chong.Experimental study of a pile-restrained floating breakwater constructed of pontoon and plates[J].Chinese Ocean Engineering Society,2010,24(1)：183-190.

[18]Hsu H H,Wu Y C.Scattering of water wave by a submerged horizontal plate and a submerged permeable breakwater[J]. Ocean Engineering,1998,26(4)：325-341.

Study on hydrodynamic characteristics of submerged upper arc-shaped plate type breakwater

WANG Ke1,SHI Peng-fei1,CHEN Yu-chao1,BIAN Jiang1,XIN Han1,CHENG Xiao-ming2
(1.State Key Laboratory of Structural Analysis for Industrial Equipment,Department of Engineering Mechanics,Dalian University of Technology,116024,China;2.China Ship Scientific Research Center,Wuxi 214082,China)

Based on wave radiation and diffraction theory,a new upper arc-shaped plate type breakwater is investigated by using boundary element method(BEM).By comparing with other three type breakwater(lower arc-shaped plate,single horizontal plate and double horizontal plates),this new type breakwater was proved more effective.The exiting force,transmission coefficient and reflection coefficient are analyzed.In order to reveal the wave elimination mechanism of this type breakwater,the velocity field around breakwater is obtained.The results show that：(1)The sway exiting force is minimal.(2)When ratio of submergence and wave amplitude is 0.05,the wave elimination effecting will increase 50%than the other three type breakwater.(3)The obvious backflow is found above the plate in velocity field analysis.

upper arc-shaped plate structure;boundary element method;transmission coefficient; velocity analysis of fluid field

TV131.2

：Adoi：10.3969/j.issn.1007-7294.2016.05.005

1007-7294（2016）05-0549-09

2016-02-27

国家重点基础研究发展计划（2013CB036101）；国家自然科学基金（51379037）

王 科（1970-），男，副教授，E-mail：kwang@dlut.edu.cn；施鹏飞（1990-），男，硕士。