海洋拖曳系统的船/缆/体耦合模型研究
2016-05-03苑志江金良安蒋晓刚郑智林
苑志江,金良安,迟 卫,蒋晓刚,郑智林
(海军大连舰艇学院,辽宁大连116018)
海洋拖曳系统的船/缆/体耦合模型研究
苑志江,金良安,迟 卫,蒋晓刚,郑智林
(海军大连舰艇学院,辽宁大连116018)
为进一步提高海洋拖曳系统在不同情况下运动响应的预测精度,将拖曳母船、拖缆和拖曳体三者视为一个相互作用的整体,利用其耦合边界条件,将拖缆顶端和底端的张力及其产生的力矩,分别与船舶操纵性运动方程(MMG模型)和拖体六自由度运动方程相结合,利用拖缆的有限差分方程,建立了船/缆/体三者耦合模型,进而采用数值计算方法,对比分析了该模型与常规算法。结果表明,该模型考虑船/缆/体三者的耦合影响,可更加准确全面地反映拖曳母船的速度、旋回半径、横摇角等操纵性特征以及拖曳体的深度、姿态等信息所受到的影响,从而为准确预报海洋拖曳系统的运动响应提供更为直观、科学的理论依据。
船舶;海洋拖曳系统;耦合模型;拖缆;拖曳体
0 引 言
海洋拖曳系统作为一种有效的水下探测平台,已被日益广泛地应用于海洋研究、监测与水声对抗等诸多领域,并发挥着越来越重要的作用,它通常由拖曳母船、拖缆和拖曳体等部分组成[1]。实际工作时,拖曳母船、拖缆和拖曳体受到的流体作用力具有明显的非线性特点[2],母船通过拖缆提供拖曳体运动驱动力的同时,拖曳体受到的流体作用力也会通过拖缆反作用于母船,三者任一运动状态的改变,均会影响到整个系统的运动状态。三者之间存在的这一耦合影响作用,使得系统在不同情况下运动响应特性的准确预报成了一个难点问题,这也是拖曳系统设计过程中必须考虑的一个重要方面[2-3],具有重要的工程应用价值。为此,国内外学者特针对海洋拖曳系统水动力理论模型进行了广泛深入的研究,以提高其设计的科学性和合理性。
当前,有关海洋拖曳系统的水动力理论模型研究成果,可分为拖缆模型和拖曳体模型两个方面。拖缆理论模型主要包括集中质量法模型[4-5]、有限元法模型[6-7]、有限差分法模型[8-10]和直接积分法模型[11]等四种,前两种在海洋拖曳系统中运用最为广泛,特别是有限差分法更适合计算大时间步长的计算情况[2]。关于拖曳体理论模型研究方面,部分学者将拖曳体视为球状物体[12-13],其拖曳体不具有姿态信息,这与实际物理情况差距较大,为了更加准确地描述拖曳体的运动,一些学者采用刚体六自由度运动方程[5,14]。然而,当前有关海洋拖曳系统的研究,往往鉴于拖曳母船的巨大质量,而忽略母船与缆/体之间的耦合影响作用,直接将拖曳母船的运动信息代入拖缆和拖曳体的运动模型当中,例如,在进行拖曳系统旋回运动仿真计算时,将拖点的航速和回转半径视为常数,忽略进入回转圈的过程,且未考虑回转过程中船速降低的影响,同时拖船自身运动对于缆/体的影响也被忽略,这一系列均会对整个系统的预报精度产生明显影响,特别是当母船相对较小,而拖曳系统其它部分质量相对较大时,造成的误差可能很大[15]。
目前,针对这一耦合影响问题进行的研究很有限,仅有拖缆对船/缆、缆/体两者耦合模型等部分成果[9-10,15-16],而关于母船、拖缆和拖曳体三者耦合作用影响的全面分析,则国内外均未见文献报道。为此,本文将拖曳母船、拖缆和拖曳体视为一个相互影响的整体,充分考虑船/缆/体三者间的耦合影响,将拖缆顶端和底端的张力及其力矩,分别与舰船操纵性运动方程和拖曳体六自由度运动方程相结合,利用耦合边界条件,建立船/缆/体的耦合模型,以预报各种机动条件下拖缆和拖曳体的运动响应和拖曳母船运动状态的改变。这对于保证整个拖曳系统的高效运行和精确实施控制,具有现实意义和理论价值,特别是可作为一种设计工具,在设计初期即可充分考虑各种机动情况,以设计更加科学高效的拖曳系统,从而代替造价昂贵的原型试验。
1 耦合模型的建立
1.1 耦合模型的建立思想
为了便于分析系统的运动特性,并建立整个系统的运动模型,本文引入了4个右手直角坐标系,即惯性坐标系,其三个坐标单位矢量为(i,j,k);拖船随体坐标系,其坐标单位矢量为(is,js,ks);拖缆局部坐标系,其坐标单位矢量为(t,n,b);拖曳体随体坐标系,其坐标单位矢量为(ib,jb,kb)。其中:惯性坐标系原点选取水面任意一点,k轴向下;船体随体坐标系,其原点一般取在船舶重心位置处,纵轴is指向船首,横轴js指向右舷,ks轴指向下方;拖缆随体坐标系,t为拖缆的切向方向,n、b为拖缆的两个法向。拖曳体随体坐标系三个轴向的方向定义与船体随体坐标系一致。
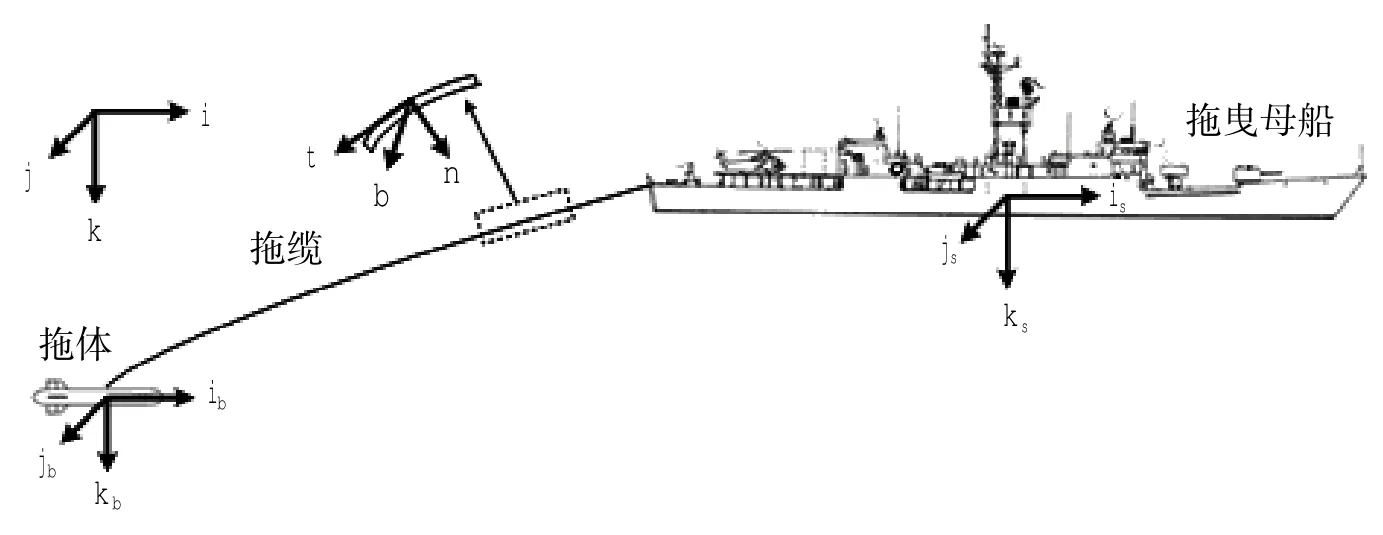
图1 海洋拖曳系统坐标系Fig.1 The coordinate frames of underwater towed system
海洋拖曳系统的船/缆/体耦合模型是指将拖曳母船、拖缆和拖曳体视为一个耦合作用的整体,从而建立整个系统运动模型。该模型建立的基础为拖缆运动模型(有限差分法)、拖曳母船操纵性运动模型(MMG模型)和拖曳体运动模型(刚体六自由度运动方程)。首先,由于拖缆顶端与拖曳母船相连接,则拖缆顶端的拉力及其产生的力矩,将会影响拖曳母船的运动响应,与此同时,拖曳母船的运动也会通过拖缆顶端传输至拖缆和拖曳体,基于此关系,可将拖缆顶端张力及其产生的力矩引入拖曳母船操纵性运动模型,从而实现船/缆的耦合,同理,也可建立缆/体的耦合;其次,由于拖缆顶端和底端分别与拖曳母船和拖体具有相同的速度,则可建立船/缆和缆/体耦合边界条件;最后,将上面建立的方程联立,从而完成船/缆/体耦合方程组的建立。
构建海洋拖曳系统耦合模型的另一个关键问题是建立其数值求解算法。由于三者的运动模型均为非线性方程,且存在着非线性耦合影响,这就决定整个系统运动模型的非线性特点。针对这一复杂的非线性方程组,难以直接求得其解析解,只能采用数值计算的方法,实现系统运动模型的求解。建立数值计算方法的基本思路为:使用中心有限差分法,将拖曳母船、拖缆和拖曳体的运动模型以及耦合边界条件,分别在时间和空间上进行离散,将整个系统模型中包含的偏微分方程组和微分方程组,均变为差分方程的形式,组成整个系统的非线性代数方程组,进而使用牛顿迭代算法求解。
1.2 耦合模型建立的基础
(1)拖缆运动模型
拖缆运动模型采用有限差分法[8],假设拖缆为细长、柔性、圆柱形,且拉力随时间变化。根据拖缆上的任意一点的力平衡,可得矢量方程式:

式中:s表示缆上一定点到上端点之间未伸长前的缆长;T为拖缆的张力;W为单位长度拖缆减去浮力后的重力;F为单位长度拖缆受到流体的作用力;B为单位长度拖缆的惯性力,即达朗伯力;a为拖缆运动加速度。
通过推导,拖缆的运动控制方程可写成如下的偏微分方程[9]:

在拖缆上任意一点,其拖缆的局部坐标与惯性坐标系之间的关系由下式确定:

其中:[D]为拖缆的局部坐标与惯性坐标之间的转换矩阵[9]。
(2)拖曳母船操纵运动模型
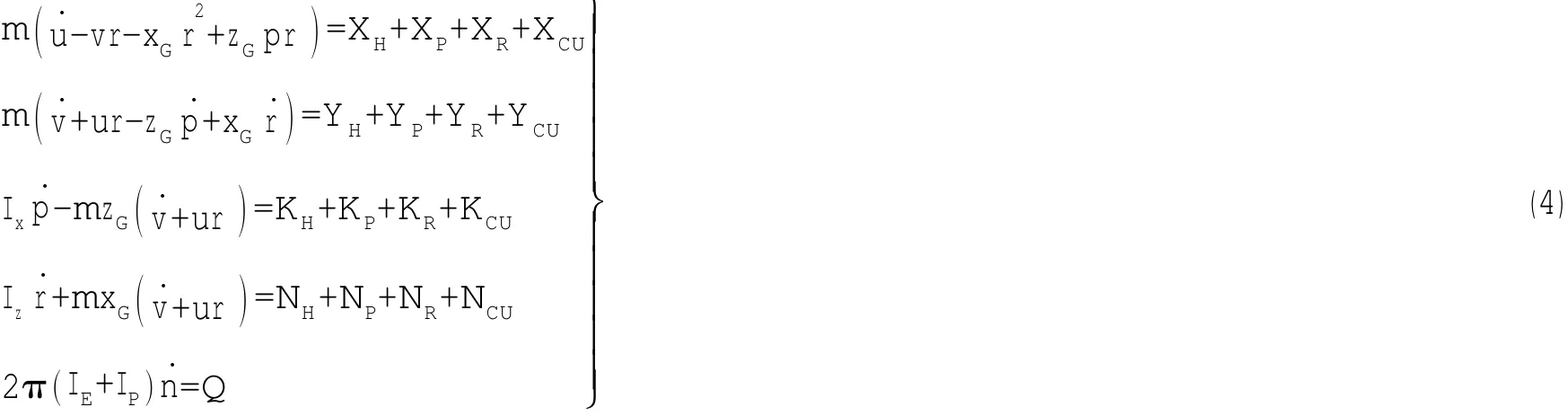
拖曳母船操纵运动模型借鉴分离式MMG操纵运动数学模型[17],即拖曳母船在桨、舵操纵下的四自由度(纵向、横向、横摇、艏向)运动方程可写为:式中:m表示拖曳母船的质量;xG和zG表示拖曳母船质心在船体坐标系下的坐标;Ix和Iz分别表示拖曳母船绕is和ks轴的转动惯量;u、v、p和r分别为船舶的纵向速度、横向速度、横倾角速度和艏向角速度;为其响应的加速度;下标H、R、P和CU分别表示船体、舵、桨和拖缆顶端的作用力和力矩;IE、IP分别为主机轴和螺旋桨的转动惯量;Q为主机轴和螺旋桨所受的外力矩(包括水动力矩和主机输出扭矩)。
有关船体、舵、桨受力及其力矩的计算公式可参考文献[17]。拖缆顶端张力及其力矩,可根据作用力与反作用力的原理计算得到。假设拖缆顶端的张力在拖缆局部坐标系下的表达式为TCU=[TCU0 0]T,则拖缆顶端张力在拖曳母船随体坐标系下的表达式为

式中:R( φ,θ,ψ)为船体坐标系与惯性坐标系之间的旋转矩阵,φ、θ和ψ分别为拖曳体的横摇角、俯仰角和偏航角。
拖缆顶端张力产生的力矩为

式中:rCU为拖缆顶端在拖船坐标系下的位置坐标。
(3)拖曳体运动模型
根据动量和动量矩方程,拖曳体的运动模型可以写为[10]

τ的计算方法与常规水下航行器的算法一致,详见文献[10];拖缆底端张力及其产生力矩的计算方法为,假设拖缆底端的张力在拖缆局部坐标系下的表达式为则拖缆底端拉力在拖曳母船随体坐标系下的表达式为

拖缆底端张力产生的力矩为

式中:rCE为拖缆底端在拖曳体随体坐标系下的位置坐标。
1.3 耦合模型解算的具体形式
(1)船/缆耦合边界条件
由于拖曳母船与拖缆顶端的速度相同,则可以建立船/缆耦合边界条件,如下:


(2)缆/体耦合边界条件
同理,拖曳体与拖缆底端的速度相同,则可以建立缆/体耦合边界条件,如下:
(3)拖缆运动控制方程的离散表示
拖缆离散使用中心有限差分法,即将拖缆在空间上沿其长度方向,离散成为N个微元Δsj,时间上离散为一系列的时间步长Δti。拖缆的节点编号从1至N+1,其中第1点为顶端,第N+1点为底端,每个节点都包含6个节点变量则(2)式在时间和空间上离散的差分方程形式为:
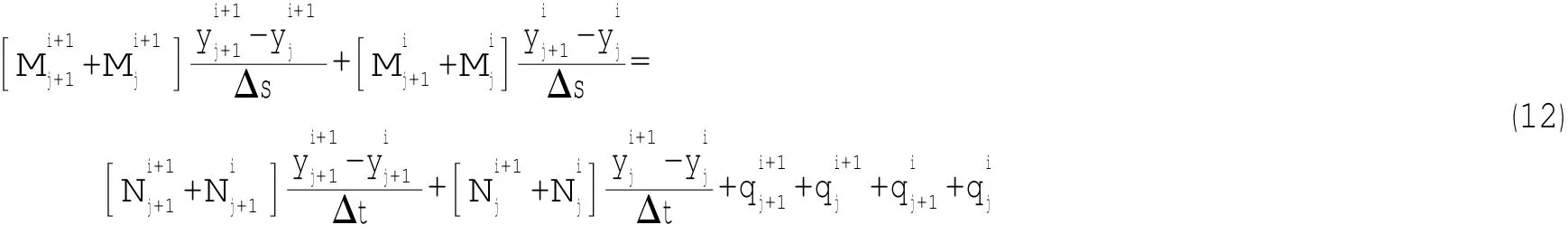
其中:上标i表示第i步时间,下标j表示第j段拖缆微线段。沿拖缆一共有6N个如(12)式形式的差分方程。
(4)拖曳母船操纵运动模型的离散表示
当构建(11)式时,可建立3个方程,但引入了拖曳母船的运动变量,可将(4)式在时间上进行中心有限差分,可得
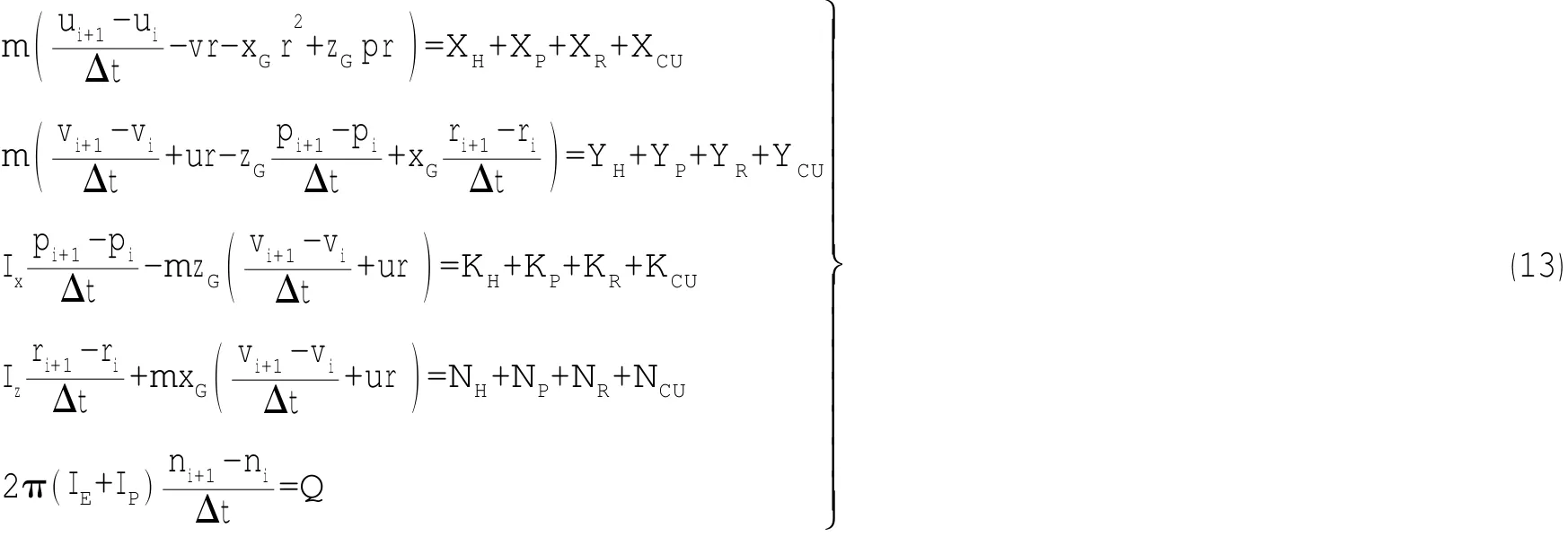
(5)拖曳体运动模型的离散表示
在构建(12)式时,又引入了12个有关拖曳体运动信息的未知变量,则可通过拖曳体运动控制方程求解得到,即将(8)式在时间上中心离散,具体如下:
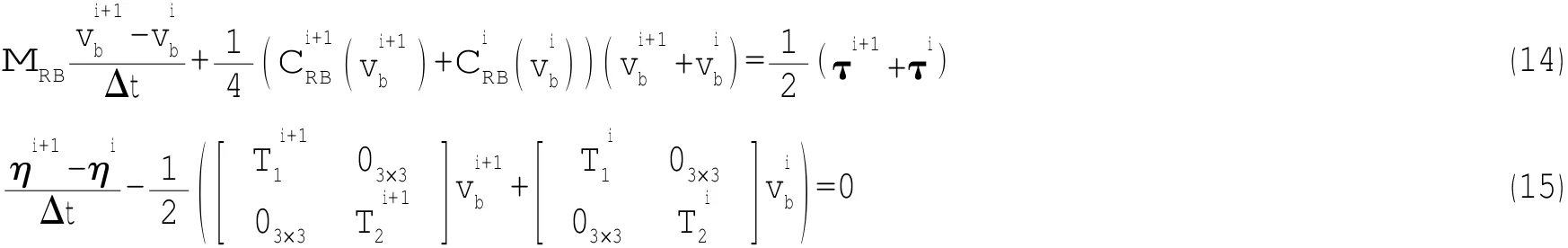
通过(14)、(15)式可得到12个差分形式的非线性方程,将(10)-(15)式联立,便可得到整个系统运动方程的离散形式,共包含了6(N+1)+16个代数方程,形成封闭方程组,使用牛顿迭代算法便可进行定解。
2 数值计算与分析
本部分将采用数值计算的方法,检验船/缆/体耦合模型的正确性,分析海洋拖曳系统在稳态运动和拖曳母船机动时的运动响应,并与常规算法(直接将拖曳母船运动信息代入缆/体耦合模型)的计算结果进行对比,分析两种算法之间存在的差异,阐述建立三者耦合运动模型的意义。为了行文方便,下文将拖曳母船自身运动信息直接代入拖曳系统计算的常规算法,简称为“拖船自身”,船/缆/体耦合模型,简称为“整个系统”。
2.1 系统参数设置
本文选用的拖曳系统,其拖曳母船选择一艘定螺距单桨单舵船,其具体参数设置:主尺度为115 m×25.4 m×8.5 m;排水量为8173 t;舵面积为18.03;展弦比为1.40;螺旋桨直径为5.53 m;螺距为5.02 m;伴流为0.26;推力减额为0.21。拖缆和拖曳体的物理参数设置分别参见表1和表2。

表1 拖缆参数设置Tab.1 The physics coefficients of towed cable

表2 拖曳体参数设置Tab.2 The physics coefficients of towed body
2.2 稳态运动仿真与分析
稳态运动是指拖曳系统的工作环境为静水时,拖曳母船以某一恒定的速度,拖带着缆/体沿直线稳定航行的运动样式[16]。系统在不同主机工况(螺旋桨转速)时的稳态运动速度,可经仿真程序运算足够长的时间而得到。本文选择螺旋桨转速n=10、20、30和40 r/min,两种算法计算得到拖曳母船稳态速度如表3所示。由表3可见,当缆/体影响作用计入后,整个系统的拖曳速度相对于拖船自身的速度具有明显下降,当转速n=10 r/min时,降幅可达13.0%,并且不同螺旋桨转速时,降幅有所不同,速度越低,其降幅越大,即缆/体对拖曳母船的影响更为明显。
由于计入缆/体耦合影响后,整个系统的拖曳速度与拖船自身的航速存在差异。这将影响系统受到的流体作用力,因此,在进行稳态运动分析时,为保证拖曳系统缆形和张力分布等信息的预报精度,不可忽略了这一影响。图2(a)给出了不同螺旋桨转速时,两种方法计算得到的稳态缆形,可以明显看出,两种方法计算得到的空间缆形具有一定的差异,计入缆/体耦合影响后的系统深度要大于相同转速下,常规算法计算得到的系统深度,并且转速越低两者之间的差距就越明显。与此同时,由图2(b)可看出拖缆的张力分布也存在差异,船/缆/体耦合模型计算得到的张力分布要小于常规算法的计算结果,并且拖曳速度越大,这一差异越为明显。
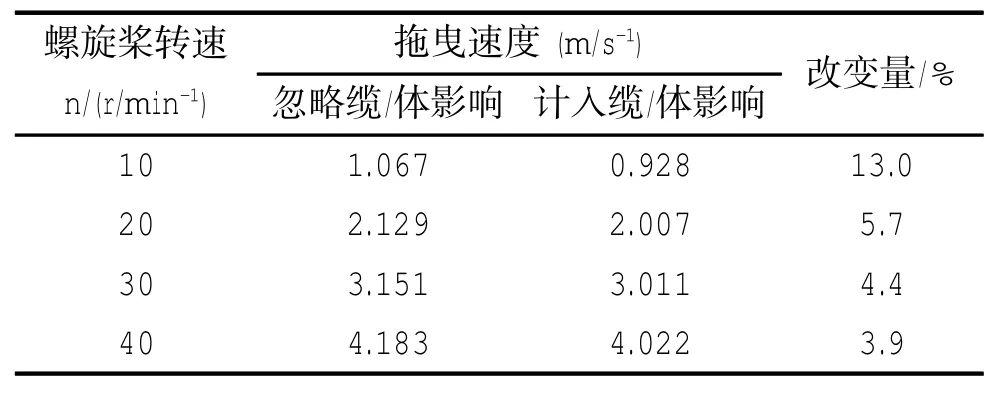
表3 不同主机工况时拖曳系统的速度Tab.3 The velocity at different engine condition
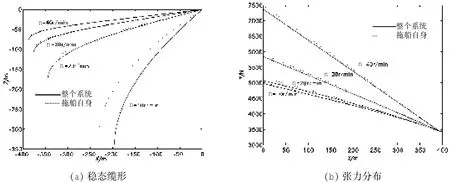
图2 不同螺旋桨转速时缆形及其张力分布Fig.2 The cable configurations and tension distribution
当采用船/缆/体三者耦合模型进行海洋拖曳系统稳态运动预报时,通过与常规算法计算结果进行对比分析,可知当计入三者之间耦合影响时,整个系统在稳态速度、缆形、张力分布等方面,均存在明显的差异。因此,在进行系统稳态运动预报时,不可忽略三者之间的耦合影响。
2.3 系统机动仿真与分析
为检验拖曳母船机动时,船/缆/体三者耦合模型的正确性。拖曳母船螺旋桨转速分别选择n=10、20、30和40 r/min,舵角为10°,进行360°旋回运动。假定系统从稳定直航状态开始作旋回,逐渐进入稳定旋回状态,当拖曳母船航向改变360°时,开始进行回舵操作,而后重新进入直线航向。
图3给出了螺旋桨转速n=10 r/min时,船/缆/体三者耦合模型计算得到的拖曳系统旋回运动的三维轨迹图,当螺旋桨转速变化时的仿真结果与图3相似。为了更好地进行对比分析,图4给出了拖曳母船旋回运动轨迹图,从图4可见,当计入缆/体影响后,拖曳母船的旋回半径会有所减小,即拖曳系统使得拖曳母船的回转性能变好,事实上拖曳系统以拖缆顶端张力的形式作用在船体上,导致这一张力分解得到的纵向力和横向力,改变拖曳母船的回转性能,其中纵向力与阻力方向相同,使得船舶回转中速度降低,具有提高回转性能的趋势。并且,由图5可以看出,在旋回的过程中,拖曳体位于拖曳母船回转轨迹内侧,即横向力的方向为指向拖曳母船轨迹内侧,具有增大舵效的作用,即可提高船舶回转性能。
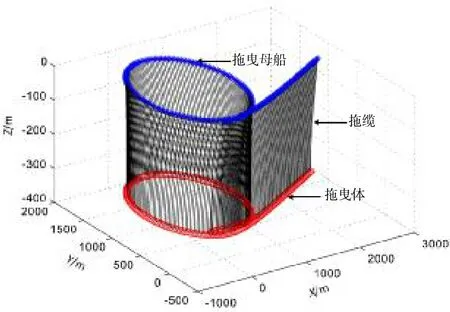
图3 拖曳系统三维轨迹图Fig.3 The trajectory of underwater towed system
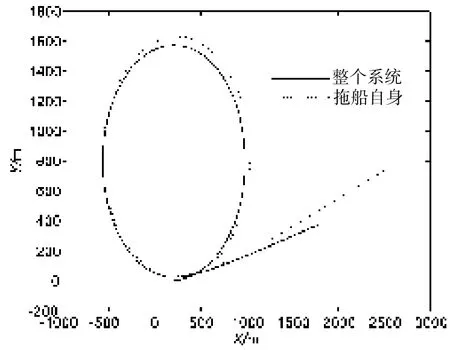
图4 拖曳母船回转轨迹Fig.4 The trajectory of towing ship
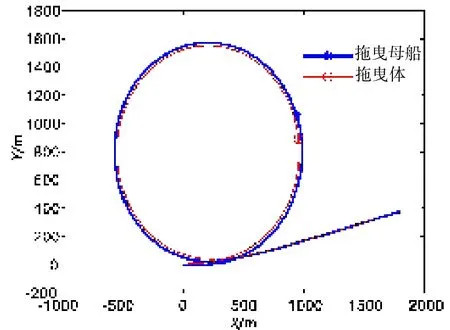
图5 拖曳系统运动轨迹俯视图Fig.5 The trajectory of towing ship
由船舶操纵性理论可知,船舶在旋回过程中其运动状态会呈现强烈的非线性变化,其轴向速度、横向速度和横摇角等是重要操纵性参数[30]。根据拖曳系统稳态速度的对比结果,可知拖曳母船旋回过程中其旋回速度也必会受到影响。图6(a)和(b)分别给出了船舶旋回过程中其轴向速度和横向速度的变化历程,其中,虚线代表拖船自身(忽略缆/体对船影响)旋回运动时的速度变化,实线代表船/缆/体三者耦合模型计算结果,可见拖曳母船的横向和轴向速度会发生非线性变化,并且,当计入缆/体影响后,计算得到横向和轴向速度,均小于常规算法计算得到的结果,两者之间存在一定的差值,并且拖曳母船的速度越低,这一差值越大。
当计入缆/体影响后,拖曳母船除了其轴向和横向速度会受到影响外,其横摇角也是一项重要检测指标。图7给出了分别采用两种算法得到拖曳母船旋回过程中,其横摇角的变化历程。从图中可以看出,当计入缆/体影响后,拖曳母船的横摇角会有所降低。
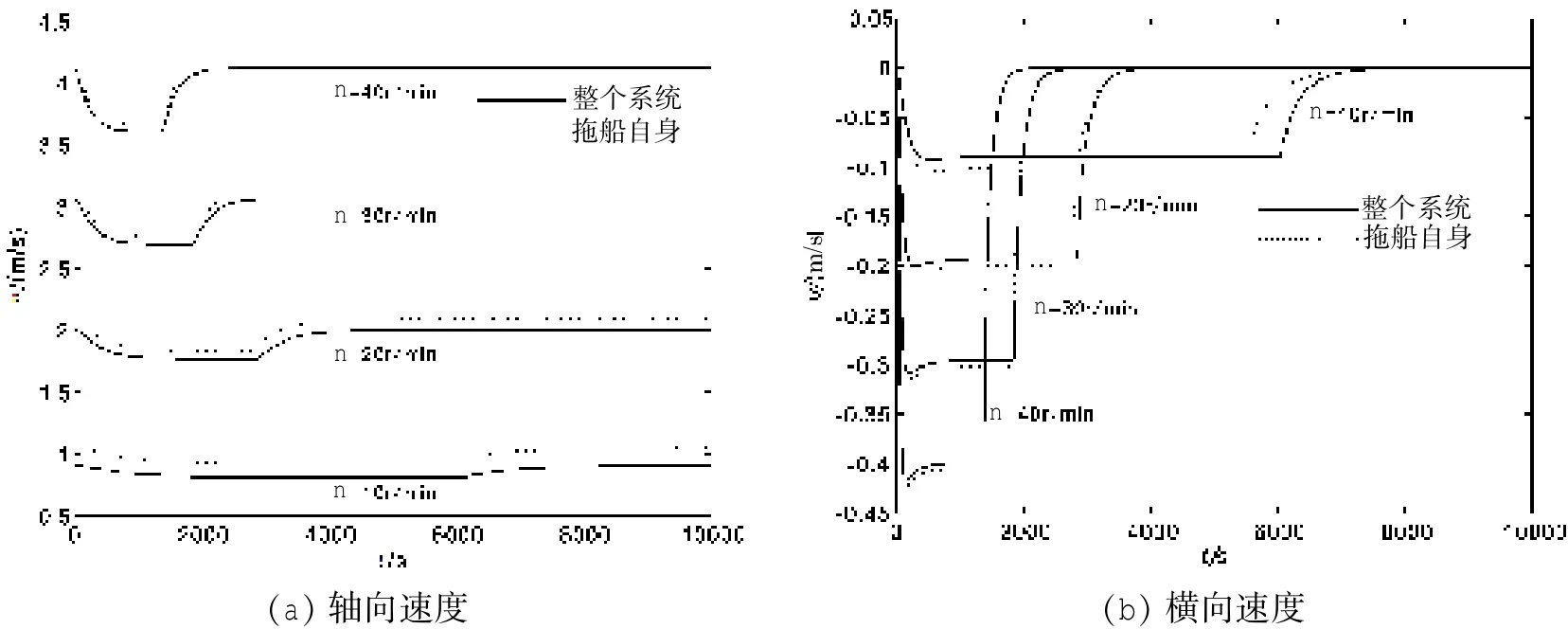
图6 船舶旋回过程中速度变化Fig.6 The velocity of towing ship at different rudder angle
由图6可知,在拖曳母船旋回运动过程中其轴向和横向速度会明显变化,这也必将使得拖缆和拖曳体受到的流体作用力发生改变,从而影响拖曳体的深度。图8给出了旋回过程中拖曳体深度变化的历程图。从图中可以看出,当拖曳母船开始旋回机动时,拖曳母船轴向速度降低,导致受到的流体作用力降低,拖曳体深度变大,随着旋回机动的进行,轴向速度趋于稳定,拖曳体的深度逐渐趋于稳定,当拖曳母船恢复直线航行时,拖曳体的深度逐渐减小,最终达到旋回机动前的稳态数值。并且,由图8还可明显看出,当计入缆/体影响后计算得到拖曳体深度,与常规算法计算得到的深度具有明显的差距,并且,拖曳母船航速越低时,这一差距越为明显。

图7 拖曳母船横摇角Fig.7 The velocity of towing ship at different rudder angle
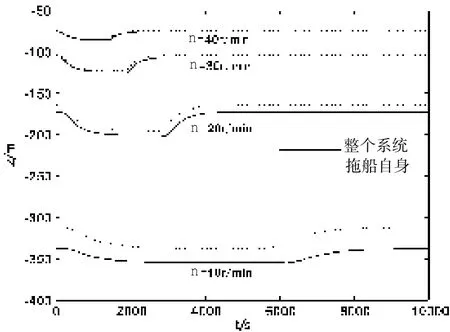
图8 船舶旋回过程中速度变化Fig.8 The velocity of towing ship at different rudder angle
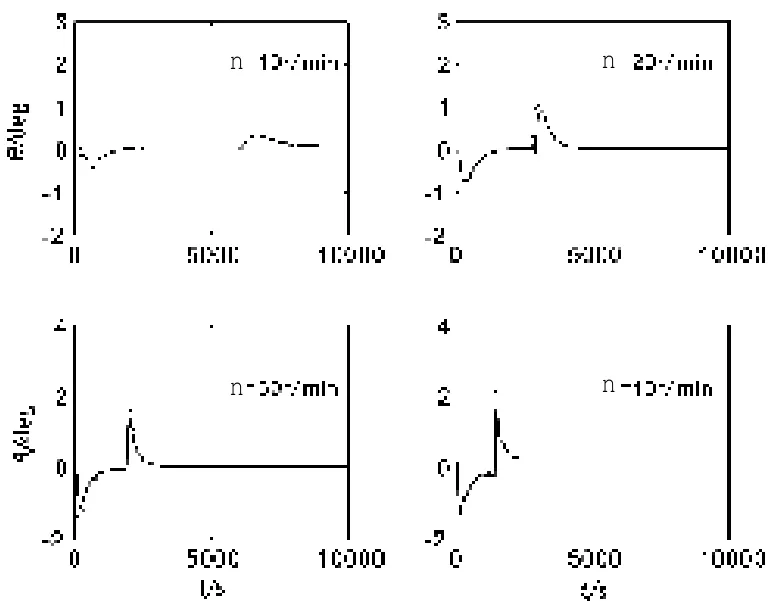
图9 船舶旋回过程中速度变化 Fig.9 The velocity of towing ship at different rudder angle
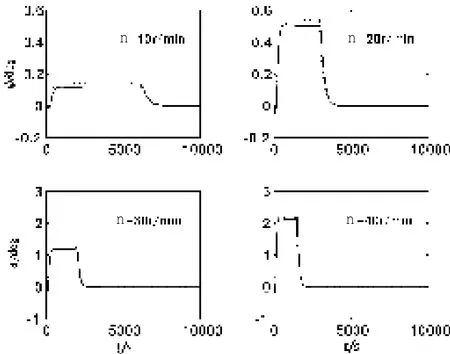
图10 船舶旋回过程中速度变化Fig.10 The velocity of towing ship at different rudder angle
在拖曳母船旋回过程中,拖曳体的姿态也会发生非线性变化,图9和图10分别给出了拖曳体俯仰角和横摇角的时间变化历程(实线表示“整个系统”,虚线表示“拖船自身”)。由图9可以看出,当开始旋回运动时,拖曳体俯仰角首先出现负值,这表示拖曳体俯首运动,随着旋回运动的进行,拖曳体的俯仰角逐渐达到某一数值,当拖曳母船再次进入直航时,拖曳体俯仰角增大,开始仰首运动,当拖曳母船航速逐渐趋于稳定时,拖曳体的俯仰角逐渐达到未旋回运动时的状态。从图中可看出,计入缆/体影响后,拖曳体的俯仰角变化有所降低,主要是缆/体产生的作用力对于船舶的俯仰运动产生了阻尼作用。同理,在旋回过程中,拖曳体的横摇角也会发生规律性变化,且计入缆/体影响后,其横摇角响应也有所下降(见图10)。
综上所述,海洋拖曳系统机动时两种算法得到的结果存在的一定差异,采用船/缆/体耦合模型可以更加准确地预测拖曳系统的动态响应。
3 结 语
为进一步提高海洋拖曳系统在不同情况下的预报精度,本文在充分考拖曳母船、拖缆和拖曳体耦合影响的基础上,将三者视为一个整体进行考虑,建立了船/缆/体三者耦合模型。为检验模型的正确性,采用数值仿真计算的方法,与常规计算方法进行了对比分析,数值结果表明当使用船/缆/体三者耦合模型后,相比较而言,系统运动响应表现出:
(1)拖曳母船的回转直径会变小;
(2)拖曳母船的运动速度会降低;
(3)由于拖曳系统产生的张力和力矩的作用,船舶的横摇角有所降低;
(4)拖曳体的深度会增大;
(5)拖曳体的俯仰角和横摇角会降低。
[1]Yuan Zhijiang,Jin Liangan,Chi Wei.Finite difference method for solving the nonlinear dynamic equation of underwater towed system[J].International Journal of Computational Methods,2014,11(4):85-89.
[2]吴家鸣,郁 苗,朱琳琳.带缆遥控水下机器人水动力数学模型及其回转运动分析[J].船舶力学,2011,15(8):827-836. Wu Jiaming,Yu Miao,Zhu Linlin.A hydrodynamic model for a tethered underwater robot and dynamic analysis of the robot in turning motion[J].Journal of Ship Mechanics,2011,15(8):827-836.
[3]王海波.水下拖曳升沉补偿液压系统及其控制研究[D].杭州:浙江大学,2009. Wang Haibo.Research on the underwater towed heave compensation hydraulic system and control strategies[D].Hangzhou: Zhejiang University,2009.
[4]Walton T S,Polachek H.Calculation of transient motion of submerged cables[J].Mathematics of Computation,1960,14: 27-46.
[5]Buckham B,Nahon M.Dynamics and control of a towed underwater vehicle system,part I:model development[J].Ocean Engineering,2003,30:453-470.
[6]Garrett D L.Dynamic analysis of slender rods[J].Journal of Energy Resources Technology,1982,104:302-306.
[7]Leonard J W,Nath J H.Comparison of finite element and lumped parameter methods for oceanic cables[J].Engineering Structures,1981,3:153-167.
[8]Ablow C M,Schechter S.Numerical simulation of undersea cable dynamics[J].Ocean Engineering,1983,10:443-457.
[9]孙洪波,施朝键,林文锦.船—缆拖曳系统操纵性能分析[J].船舶力学,2015,19(11):1325-1333. Sun Hongbo,Shi Chaojian,Lin Wenjin.Analysis of maneuverability of towing cable ship system[J].Journal of Ship Mechanics,2015,19(11):1325-1333.
[10]杜晓旭,宋保维,潘 光.AUV水下回收过程中的操纵性仿真研究[J].船舶力学,2011,15(8):837-843. Du Xiaoxu,Song Baowei,Pan Guang.Simulation of an AUV underwater recovery[J].Journal of Ship Mechanics,2011,15 (8):837-843.
[11]Sun Y,Leonard J W,Chiou R B.Simulation of unsteady oceanic cable deployment by direct integration with suppression [J].Ocean Engineering,1994,21:243-256.
[12]沈晓玲.深海拖曳系统动力学分析研究[D].上海:上海交通大学,2011. Shen Xiaoling.Research on the hydrodynamic of deep underwater towed system[D].Shanghai:Shanghai Jiao Tong University,2011.
[13]Grosenbaugh Mark A.Tansient behavior of towed cable systems during ship turning maneuvers[J].Ocean Engineering, 2007,34:1532-1542.
[14]Feng Z,Allen R.Evaluation of the effects of the communication cable on the dynamics of an underwater flight vehicle[J]. Ocean Engineering,2004,31:1019-1035.
[15]王 飞,黄国樑,伍生春.水下拖曳系统缆/船耦合运动模拟[J].上海交通大学学报,2011,45(4):570-575. Wang Fei,Huang Guoliang,Wu Shengchun.Dynamic research on the coupling response of cable-towing ship system[J]. Journal of Shanghai Jiao Tong University,2011,45(4):571-575.
[16]Wang Zhibo,Sun Gang.Parameters influence on maneuvered towed cable system dynamics[J].Applied Ocean Research, 2015,49:27:41.
[17]吴秀恒.船舶操纵性[M].北京:国防工业出版社,2005. Wu Xiuheng.Ship maneuverability[M].Beijing:National Defence Industrial Press,2005.
Research on the coupling model of underwater towed system
YUAN Zhi-jiang,JIN Liang-an,CHI Wei,JIANG Xiao-gang,ZHENG Zhi-lin
(Dalian Naval Academy,Dalian 116018,China)
In order to predict the behaviors of the underwater towed system under different conditions more precisely,the towing ship,towed cable and towed vehicle are treated as a whole.Using the boundary condition of the system,the tension and moment of the towed cable’s upper end and bottom end are used into the MMG model of ship and the six freedoms equation of towed vehicle respectively.Moreover,coupling with the finite difference method of towed cable,the couple model of whole system is established.The numerical method is developed based on this model to predict the behaviors of the underwater towed system.Compared with normal method,the numerical results indicate that the velocity,turning radius,roll angle of towing ship and the depth,attitude of towed body are affected.This model can be used as the basic theory for predicting the behaviors of underwater towed system.
ship;underwater towed system;coupling model;towed cable;towed body
U661.33
:A
10.3969/j.issn.1007-7294.2016.10.005
1007-7294(2016)10-1252-10
2016-04-24
国防预研项目(5131402031)
苑志江(1983-),男,博士研究生,讲师,E-mail:yuanyr0531@163.com;金良安(1966-),男,教授,博士生导师。
