阻抗源电流型变流器的基本原理和研究现状

李大飞， 郭文勇， 全生财

(1. 中国科学院电工研究所，北京 100190； 2. 中国科学院大学， 北京 100049；3. 中国科学院应用超导重点实验室， 北京 100190)

阻抗源电流型变流器的基本原理和研究现状

李大飞1,2,3， 郭文勇1,3， 全生财1,2,3

(1. 中国科学院电工研究所，北京 100190； 2. 中国科学院大学， 北京 100049；3. 中国科学院应用超导重点实验室， 北京 100190)

阻抗源拓扑结构由于其独特的升降压功能得到越来越多的关注，目前已经应用于直交、交直以及相位频率均变化的交交电路中。阻抗源变流器可以分为电流型和电压型两大类，电流型和电压型相比，具有动态响应快、限流能力强、直流回路阻抗较大和输入电压较高等优点。本文对阻抗源电流型变流器进行详细分析，介绍阻抗源电流型变流器的发展历史和研究现状，研究有代表性的阻抗源电流型拓扑结构的工作原理及其优点和应用场合，并对其未来的发展进行展望。

阻抗源; 电流型; 升降功能

1 引言

交流调速系统、燃料电池供电系统、光伏发电和风力发电等分布式发电系统以及微电网都有随负载和环境因素的变化而电压电流输出波动范围很大的特点[1]，这给电能转换提出了新的要求：变流器要能够实现大范围的升降压功能从而给负载提供稳定的电压，同时要保证负载供电的安全性和可靠性。传统电压型和电流型变流器已无法适应电能转换的新要求，针对电能转换的新要求，2002年美国密歇根州立大学彭方正教授提出了阻抗源变流器的概念，提出一种新颖变流器拓扑理论[2]，满足了电能转换更宽升降压范围的需求。近年来对其进行研究的科研机构国际上主要有美国密西根州立大学、俄亥俄州立大学、田纳西州立大学、新加坡南洋理工学院、韩国釜山大学和澳大利亚新南威尔士大学等。浙江大学率先在国内开展这方面的研究，合肥工业大学、西安交通大学、哈尔滨工业大学、南京航空航天大学等也相继开展了相关的研究工作。文献[3-5]主要研究集中在拓扑结构的建模和控制策略；文献[6-10]主要由电压型变流器的调制方法为起点进行类比，研究了应用于阻抗源电流型变流器的PWM波形调制策略；文献[11-14]主要阐述了阻抗源变流器的应用领域；文献[15-20]主要研究了其他衍生阻抗源拓扑结构；文献[21]统计出近年相关阻抗源文献发表数量，指出其呈现递增趋势。

阻抗源变流器分为电压型和电流型两大类。与电压型相比，电流型变流器具有动态响应快、限流能力强、直流回路阻抗较大、输入电压较高等优点，另外直流侧串联的电感可以对交流侧产生的无功能量起到缓冲作用。由于阻抗源电流型变流器具有上述独特的优势，本文以阻抗源电流型变流器为研究对象，全面细致地阐述阻抗源电流型变流器的发展历史、拓扑结构、电路特点、运行机制和应用场合等，并对其未来的发展进行展望。

2 基本阻抗源电流型变流器

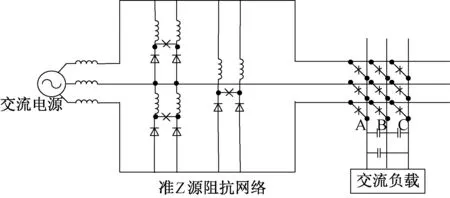
传统电流型变流器的拓扑结构如图1所示，阻抗源网络是由电感L1、L2和电容C1、C2接成X型二端口网络，又称Z源网络[2]，如图2所示。阻抗源电流型变流器是在传统电流型变流器的基础上，将阻抗源网络耦合在直流侧电源和桥式变流器之间，形成其基本拓扑结构，如图3所示。阻抗源网络由于其独特特性，允许变流桥臂瞬时开路状态的出现，为变流器主电路自由升降压提供了可能。

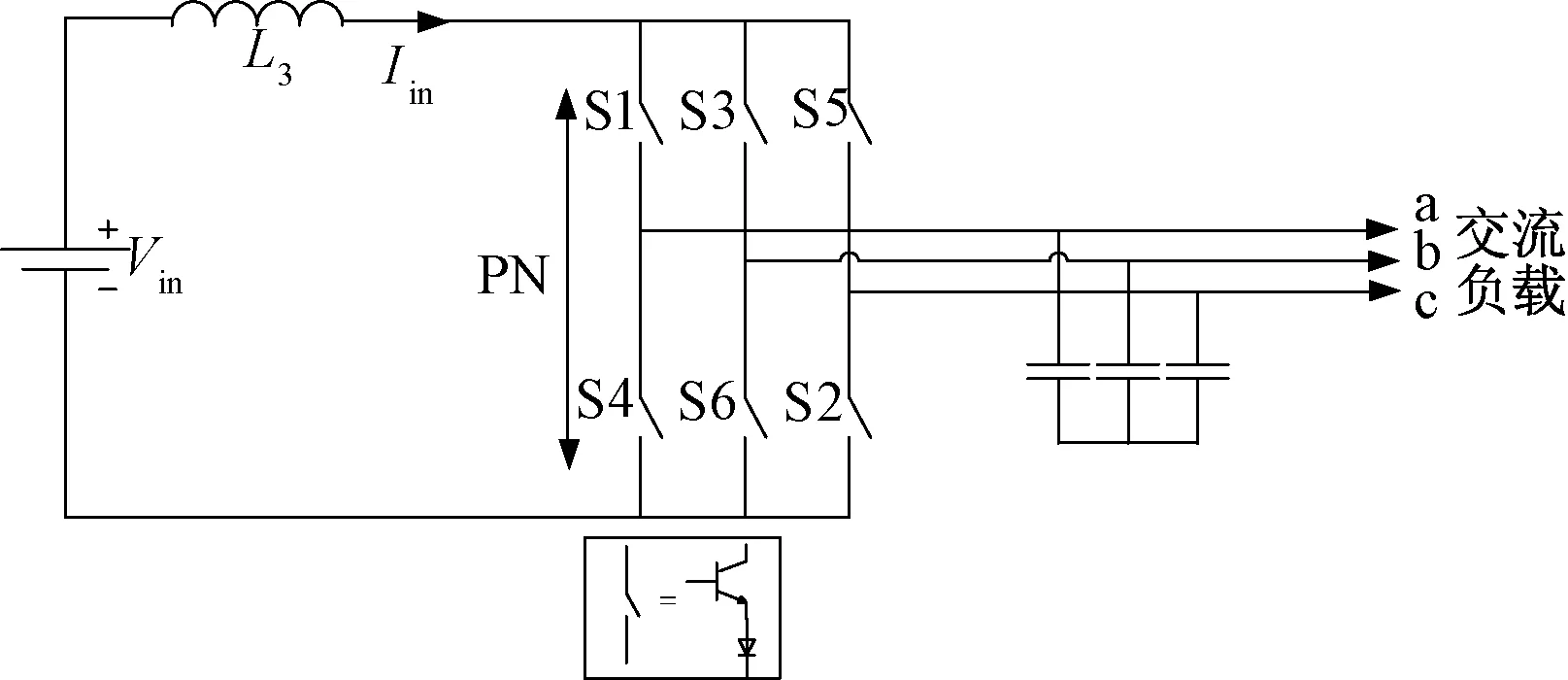
图1 传统电流型变流器的基本拓扑结构Fig.1 Basic current source converter topology

图2 基本阻抗源网络拓扑结构Fig.2 Basic impedance source topology

图3 阻抗源电流型变流器拓扑结构Fig.3 Impedance source current-fed converter topology

2.1 基本型的工作原理

基本电流型变流器有9个允许的电流矢量，分别为：①当直流环节电流作用到负载上时的6个有效矢量；②当输入端被同一桥臂的两个开关同时导通而短路的3个零矢量。电流型阻抗源变流器的独特阻抗网络允许有第10个开关矢量状态，即当所有的上臂开关管全关断或下臂开关管全关断或者六个开关均关断时，这三种状态等效为一种电路结构，产生一个额外的零状态(或矢量)，称之为开路矢量状态。传统电流源变流器电路结构由于存在大电感，开路矢量状态会损坏功率开关器件，是不允许存在的。但对于阻抗源电流型变流器中，开路矢量状态提供了独特的升降电流特性[22]。

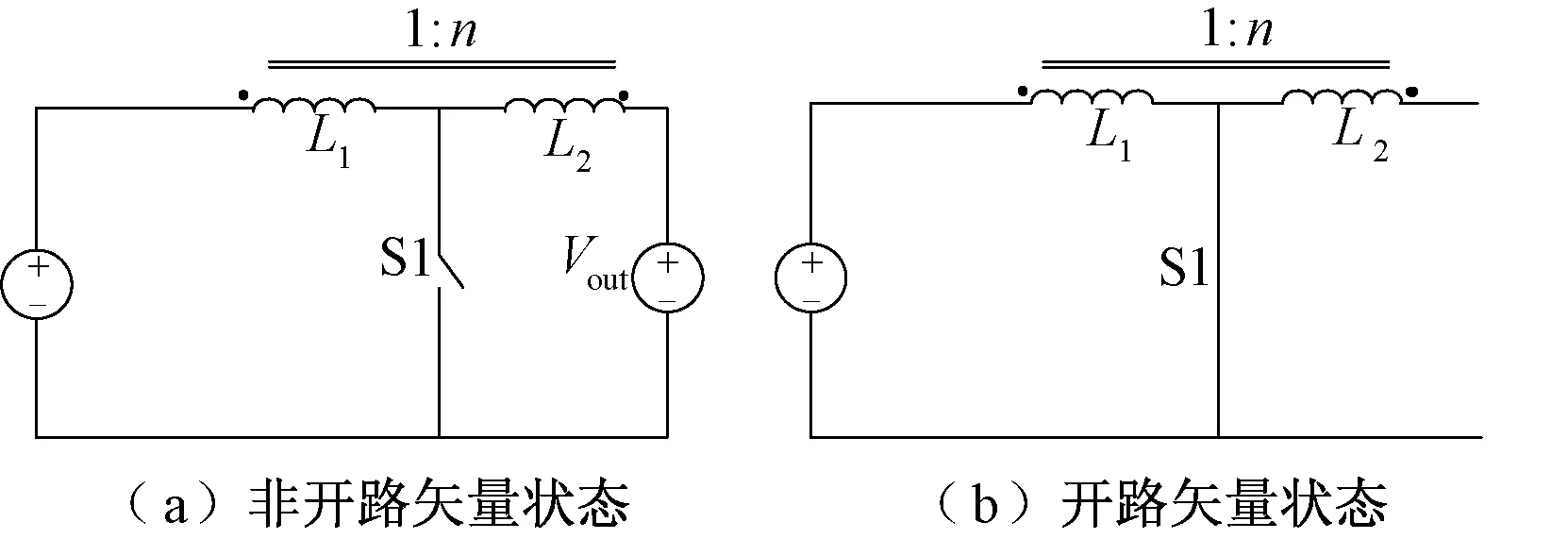
图4(a)和图4(b)为该拓扑两种不同工作状态下的等效电路。当变流器工作在6个有效状态或3个零状态时，可以等效为一个电压源。零状态下的变流器可由零值电压源来代替(即短路)，如图4(a)所示；而当变流器工作于开路矢量状态时，可以等效为开路，如图4(b)所示。

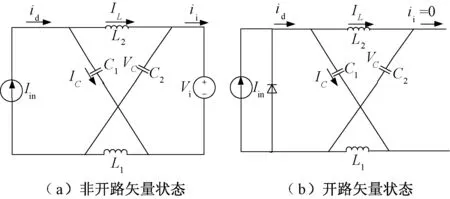
图4 电流型Z源变流器等效电路Fig.4 Equivalent circuits of current-fed Z source converter

假设图4(a)和图4(b)中的电感L1、L2和电容C1、C2具有相同的电感和电容值，阻抗源网络具有对称性，由此可以得到：

IL1=IL2=IL，IC1=IC2=IC，VC1=VC2=VC

(1)

若一个开关周期T内变流器工作于9个非开路矢量状态的时间为T1，如图4(a)所示，这时电感充电，电容器放电，有:

IC=Iin-IL,id=Iin,ii=IL-IC=2IL-Iin

(2)

式中，Iin为输入电流；ii为流入变流器电流。

若一个开关周期T内，变流器工作于开路矢量状态的时间为T0，有T0=T-T1，如图4(b)所示，这时电感放电，电容充电，有：

IC=IL,id=2IL,ii=0

(3)

在稳态下，一个开关周期T中流过电容的电流平均值为零，从式(2)和式(3)可以得到：

(4)

(5)

由图4电路可知，开路矢量状态T0内，ii=0，流入变流器的平均直流环节电流Ii为：

(6)

(7)

式中

(8)

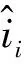
(9)

式中，M为调制因数。将式(7)代入式(9)，可以得到：

(10)

定义：

BB=MB=0-∞

(11)

根据式(1)、式(5)和式(8)，Z源网络电感电流可以描述为：

(12)

升降因子BB由调制因数M和升降因子B决定。应当注意，开路矢量状态的插入并没有影响变流器的PWM控制，因为它等效地在负载端产生零电流。能够实现的最大开路矢量状态时间受到变流器工作于零状态的时间的限制，而后者由调制因数M决定[23]。式(10)和式(11)证明了阻抗源网络的升降电流功能，说明了其工作原理。

2.2 基本阻抗源电流型变流器优点

基本阻抗源电流型变流器具有较大范围的升降功能，对其进行理论和应用的研究具有很重要的学术价值[24]，其结合了阻抗源网络和传统电流源变流器的优点，具体可概括为以下几点[25]：

(1)能够实现升降变换的功能。由于其变流器桥臂可以开路，阻抗源电流型变流器可以实现直流侧的电流升降功能，其交流输出电压电流不受输入电压限制，从而实现单级升降变换。

(2)变流器桥臂可以开路，因此由电磁干扰所造成的开关管误关断不会对变换器造成损坏。

(3)变流器同相桥臂的上下开关管之间不需要加入换流重叠时间，因此输出波形畸变率降低。

3 电流型准Z源变流器

基本阻抗源变流器存在阻抗源电容电压高于输入电压、启动冲击大、变流器体积重量大和可靠性低等缺点。基于此，彭方正教授在基本阻抗源变流器的基础上又提出改进的准Z(quasi-Z)源变流器[26]，其电路结构如图5所示。

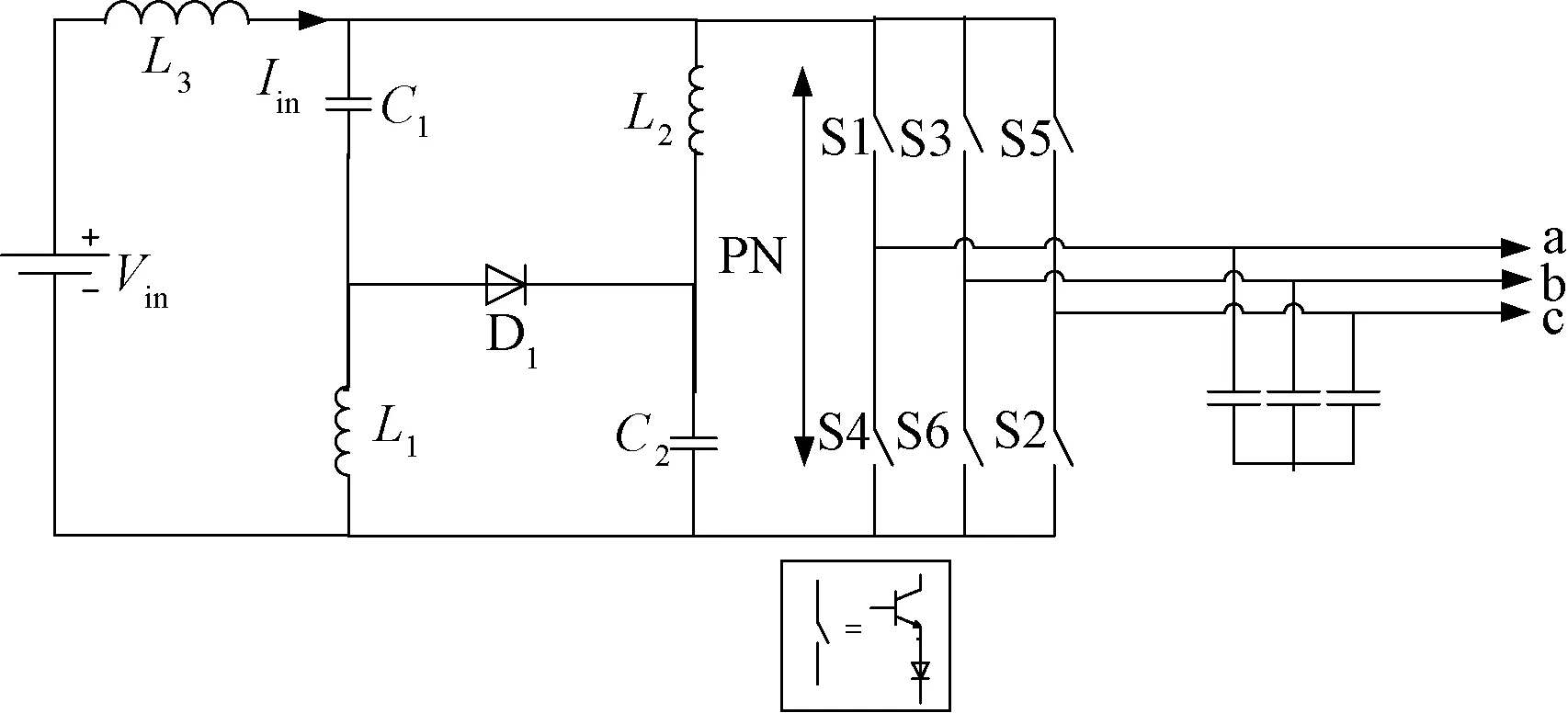
图5 电流型准Z源变流器拓扑结构Fig.5 Current-fed quasi-Z source converter topology

3.1 电流型准Z源变流器的工作原理

准Z源阻抗网络的引入，使电流型准Z源变流器可以运行于开路矢量状态，各矢量运行状态如图6所示。

图6 电流型准Z源变流器各矢量等效电路Fig.6 Equivalent circuits of current-fed qZSI

电流型准Z源变流器的等效电路有三个状态，分别为有效状态、短路零状态和开路矢量状态，在一个开关周期T内的时间分别为Ta、Tsh、Top，有效状态占空比为Da=Ta/T，余下类推为Dsh、Dop。假设Z源网络中具有相同的电感值和电容值：L1=L2,C1=C2，由电路结构的对称性可得：

VC1=VC2=VC,VL1=VL2=VL

(13)

无论在哪种矢量状态下，总满足以下关系式：

VC1+VL1=VC2+VL2=Vin+VL3

(14)

考虑到一个开关周期中准Z源网络中无源电感的平均电压为零，可得：

VC1=VC2=VC=Vin

(15)

(Vout-VC)Da+(-VC)Dsh+VCDop=0

(16)

(17)

电流连续模式下，变流器的电流增益可通过准Z源电容的安秒平衡计算，在一个开关周期内准Z源网络中电容的平均电流为零，即

IL(1-Dop)-(Iin+IL)Dop=0

(18)

(19)

(20)

流入到变流器中的电流为：

(21)

与图1中传统电流型变流器拓扑中流入变流器直流侧的等效电压Vin和等效电流Iin相比，由式(17)和式(21)可得，由于准Z源阻抗网络的引入，使流入电流型准Z源变流器的等效直流侧电压Vout和电流Ipn具有调节功能，与等效电压Vin和等效电流Iin成比例关系，其大小可由独立变量Dop和Da进行控制，实现了自由升降。

3.2 电流型准Z源变流器的应用场合及优点

电流型准Z源变流器作为电流型阻抗源变流器拓扑的发展，继承了后者优点的同时也克服了电流型阻抗源变流器的电感必须维持高电流的主要缺点。此外，当电流型阻抗源变流器用于背靠背结构变流器时，由于变流器的开关函数耦合问题，其控制是一大难题。而电流型准Z源变流器是对传统的阻抗源变流器的改进[25]。电流型准Z源变流器的拓扑结构、电路特点适用于光伏并网发电、燃料电池、混合动力汽车和电动汽车等领域，满足其电压电流波动范围大的特点[27-30]。图7和图8分别表示为其应用于混合动力汽车的拓扑结构。

图7 连续电流模式下电流型准Z源平行混合系统Fig.7 Parallel hybrid system using current-fed qZSI with continuous input current

图8 PWM整流器和电流型准Z源的串联混合系统Fig.8 Series hybrid system using PWM rectifier and current-fed qZSI

对比传统的升压整流变流器，电流型准Z源变流器具有较小的开关次数和较小的有源器件电流应力，能满足工业领域中最低的开关损耗、最低的电流纹波、最低的输出谐波和最低电压尖峰的要求。鉴于其高效率、高功率密度和低成本的特点，文献[25,31,32]已将此拓扑应用于电动马达驱动器和发电机中。文献[33]将一个功率等级为24kW的电流型准Z源变流器应用于实验室中，其功率效率达到97.6%，峰值效率达到98.2%，相比传统的两级结构，两者都提高了3%～4%，功率密度达15.3kW/ L。

电流型准Z源变流器具有如下的优点：

(1)用一级电路结构完成升降压，能量双向流动。

(2)在电动机运行状态(功率从直流侧流向交流侧)，电流源准Z源变流器输出电压可以达到输入电压的0～2倍。

(3)在发电机运行状态(功率从直流侧流向交流侧)，电流源准Z源变流器理论上可以输出零到无限大的直流电压。

(4)通过用RB-IGBT代替二极管，电流源准Z源变流器理论上可以克服电压范围区间限制，输出任意的电压值[33]。

4 含变压器的阻抗源电流型变流器

近年来，为了提高电压和电流增益，通过改进阻抗网络而衍生出许多特殊的阻抗源网络，这些技术可以分为增加开关器件技术[34, 35]、级联技术[36]和磁耦合技术[37, 38]。其中，磁耦合技术更具吸引力，其通过耦合变压器和电感可以产生高电压电流增益，且具有较少的元器件数量。接下来介绍几种含变压器的阻抗源网络拓扑结构和其工作原理。

4.1 电流型Trans-Z源变流器的工作原理

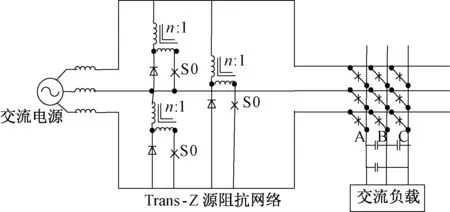
Trans-Z源变流器的阻抗网络由一对变压器和一个电容组成，其拓扑结构如图9所示。

图9 电流型Trans-Z源变流器Fig.9 Current-fed Trans-Z source converter

假设变压器具有理想匝数比，n为变压器匝数比；im为磁化电流，从变流器直流侧角度观察图9，其等效电路如图10所示。

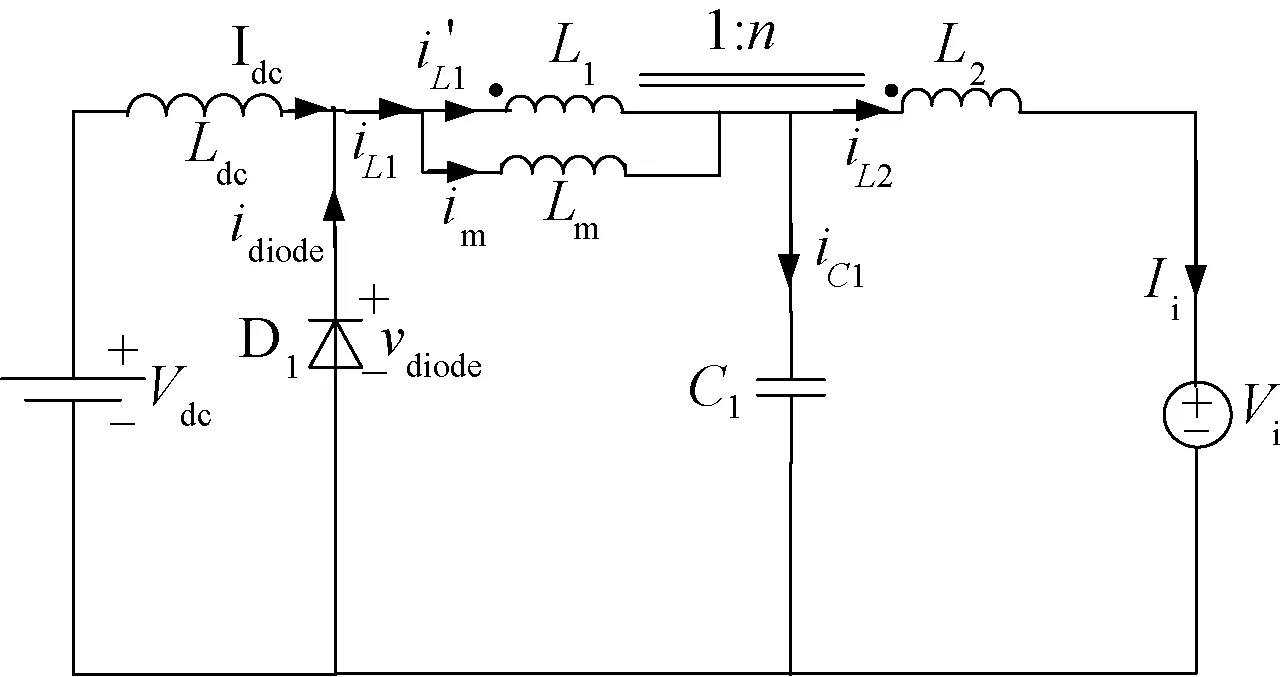
图10 电流型Trans-Z源变流器的等效电路Fig.10 Equivalent circuit of current-fed Trans-Z source converter

类似地，该电路具有开路矢量状态，其非开路矢量状态和开路矢量状态的等效电路分别如图11(a)和图11(b)所示。在非开路矢量状态下，包括有效矢量和短路零矢量，电流型变流器等效为一个电压源vi，有效状态下为线电压，短路零矢量下为零。利用KCL和变压器等效模型，由图11(a)和图11(b)可知：

(22)

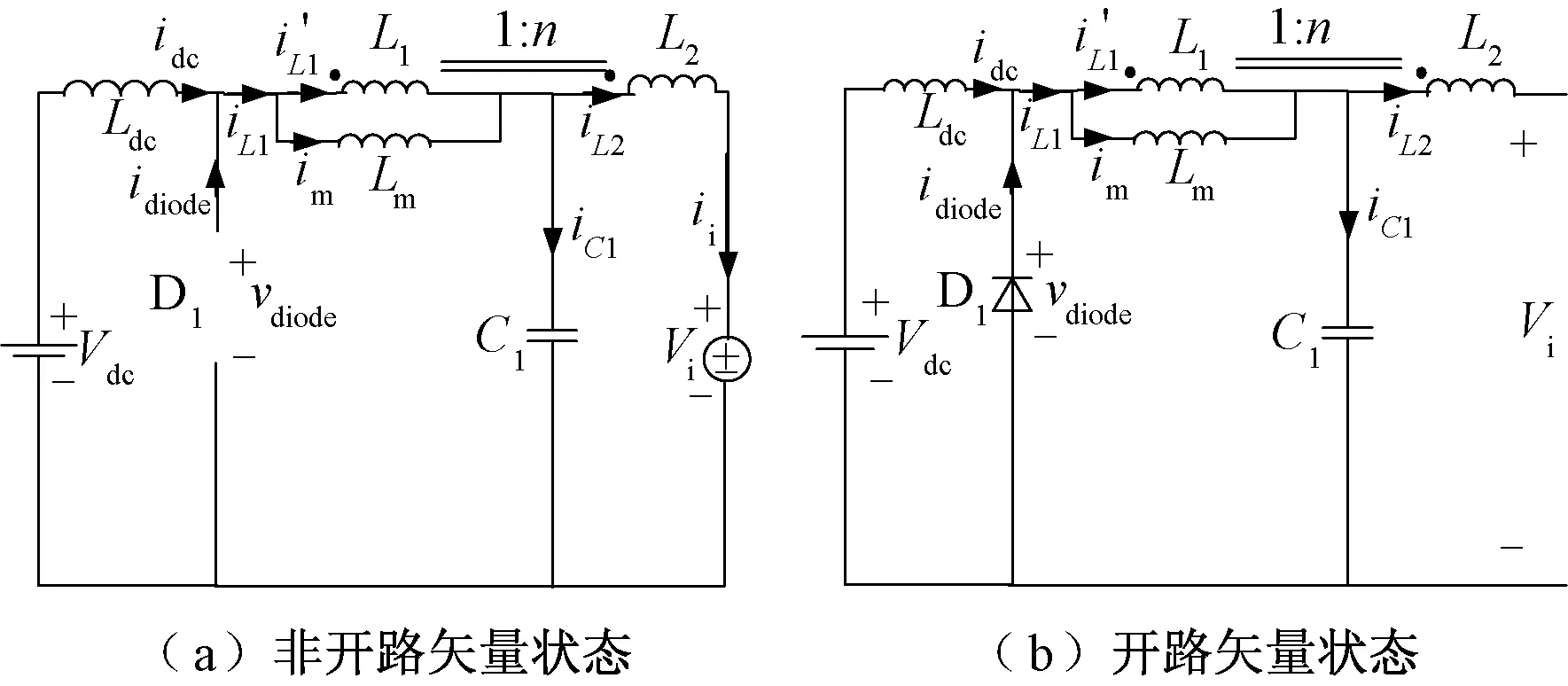
图11 电流型Trans-Z源变流器的两种等效状态Fig.11 Two equivalent circuits of current-fed trans-Z source converter

在非开路(1-Dop)T时间内，二极管关断，L1中电流iL1=idc，电容电流为：

(23)

在开路矢量状态DopT内，二极管导通，L2中没有电流流过，可以推导出此状态下电容电流为:

iC1=im

(24)

考虑到变流器在连续电流模式下运行，磁化电流和输入电流纹波较小，im和idc分别可以等效为其直流分量Im和Idc，利用电容在一个周期内的安秒平衡法则，可得:

(25)

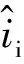
(26)

式中，B可以定义为电流的升降系数，利用匝数比n达到升降电流的目的。

4.2 电流型Trans-准Z源变流器的工作原理

电流型Trans准Z源变流器与4.1节Trans-Z源变流器的工作原理类似，拓扑结构如图12所示。将变流器等效为一个电压源的等效电路如图13所示。利用类似的分析方法，可得其工作原理如下所述。

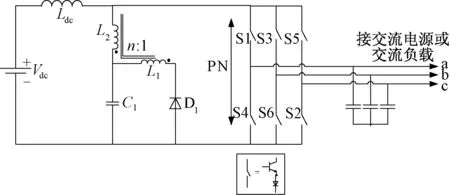
图12 电流型Trans-准Z源变流器Fig.12 Current-fed Trans-quasi-Z source converter

其开路状态和非开路状态的等效状态分别如图14(a)和图14(b)所示。在非开路矢量状态下，包括有效矢量状态和短路零矢量状态，电流型变流器等效为一个电压源vi，有效矢量状态下为三相线电压，短路零矢量下为零。利用KCL和变压器等效模型，由图14(a)和图14(b)可以分析各自电路状态方程。

图13 电流型Trans-准Z源变流器的等效电路Fig.13 Equivalent circuit of current-fed trans- quasi-Z source converter

图14 电流型Trans-准Z源变流器的两种等效状态Fig.14 Two equivalent circuits of current-fed Trans-quasi-Z source converter

在开路矢量状态DopT时间内，二极管导通，L1中有电流流过，可以推导出此状态下电容电流为：

iC1=(1+n)idc+im

(27)

在非开路(1-Dop)T时间内，二极管关断，L1中没有电流，此状态下电容电流为：

(28)

考虑到变流器在连续电流模式下运行，利用电容在一个周期内的安秒平衡法则，可得：

(29)

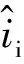
(30)

式(30)与(26)具有相同的表达形式，可见二者在本质上的统一性。

4.3 电流型Flipped-Γ源变流器的工作原理

电流型Trans-Z源变流器通过增加变压器的匝数比来得到较高的增益和调制系数，但增益越高，需要匝数比也越大，文献[39]提出了一种电流型Flipped-Γ源变流器拓扑结构，如图15所示，其能够通过较低的匝数比获得理想的升降能力。

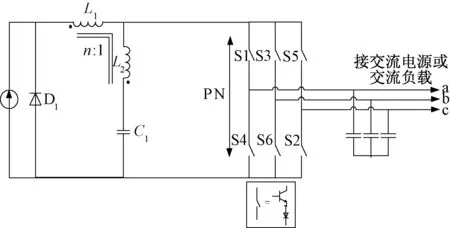
图15 电流型Flipped-Γ源变流器Fig.15 Current-fed Flipped-Γ source converter

利用同样的分析方法，其工作模式同样分为非开路矢量状态(如图16(a)所示)和开路工作状态(如图16(b)所示)。利用KCL可以得到如下等式：

(31)

图16 电流型Flipped-Γ源的两种等效状态Fig.16 Two equivalent circuits of current-fed Flipped-Γ source converter

在非开路(1-Dop)T时间内，二极管关断，L1中电流i1=Idc，利用KCL可得电容电流为：

iC=nIdc-im

(32)

在开路矢量状态DopT时间内，二极管导通，L1中电流i1=iC，可以推导出此状态下电容电流为：

(33)

考虑到变流器在连续电流模式下，稳态运行时，利用电容在一个周期内的安秒平衡法则，可得：

(34)

将im代入到非开路矢量状态下的表达式下，变流器直流侧的峰值电流可以表达为：

(35)

由式(35)可知，相比较式(30)，n取较小的值可以取得较高的增益。

4.4 电流型Trans-T源变流器的工作原理

在需要更高电流增益的应用场合下，电流型Trans-Z源变流器需要更高匝数比的变压器，这会使体积变得更大，成本变得更高，而电流型Flipped-Γ源变流器由于其增益要求匝数比的精确度高，敏感性强，设计变压器的难度增大，文献[40]提出了一种新型变流器，采用三个耦合电感组合而成的T型结构，称为Trans-T源变流器，如图17所示。

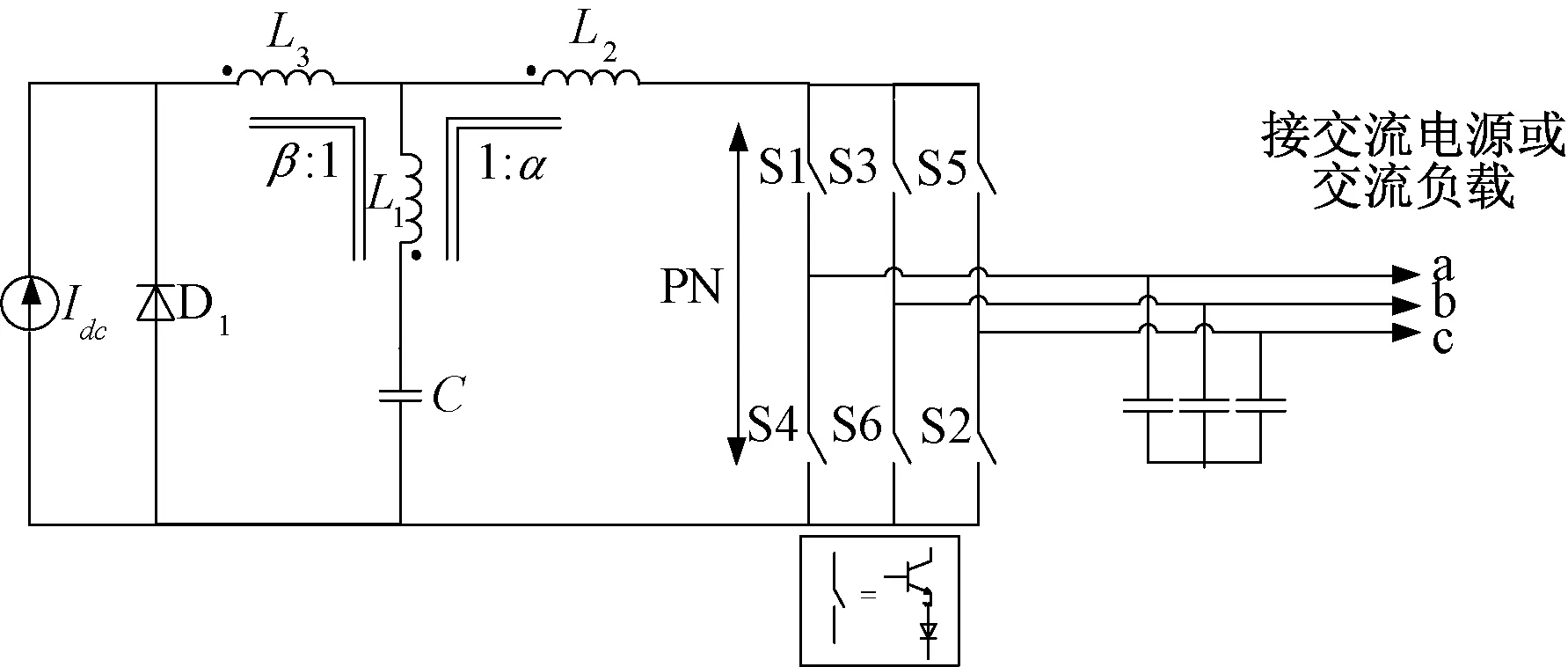
图17 电流型Trans-T源变流器Fig.17 Current-fed trans-T source converter

电流型Trans-T源变流器直流侧等效电路如图18所示。在运行过程中，同样有非开路矢量状态和开路矢量状态两种工作模式，如图19所示。根据KCL、变压器电压电流和匝数比的关系可得如下关系式：

(36)

式中，n1、n2、n3分别为三个线圈的匝数，其中n2/n1=α，n3/n1=β。

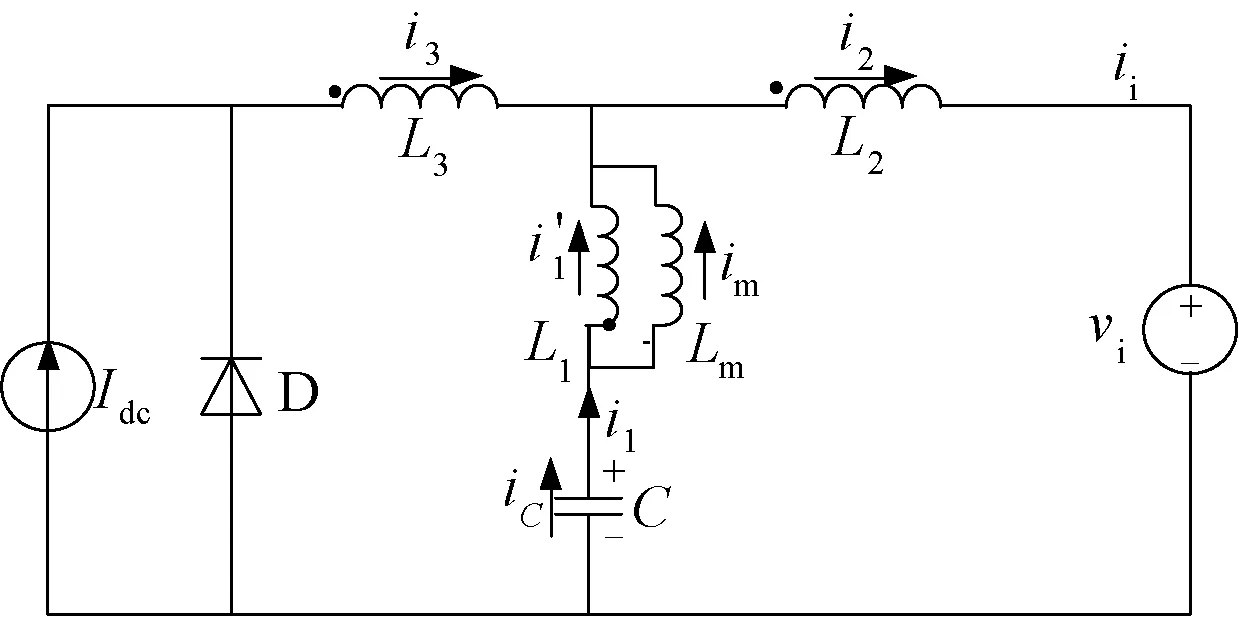
图18 电流型Trans-T源变流器的等效电路图Fig.18 Equivalent circuit of current-fed trans-T source converter

图19 电流型Trans-T源的两种等效状态Fig.19 Two equivalent circuits of current-fed Trans-T source converter

在开路矢量DopT时间内，二极管导通，变流器等效为开路，L2中没有电流流过，可以推导出：

(37)

(38)

在非开路(1-Dop)T时间内，二极管关断，此时电路中的电流关系为：

(39)

可得电容电流为：

(40)

考虑到变流器在连续电流模式下运行，利用电容在稳态下一个周期内的安秒平衡法则，可得：

(41)

将im代入式(39)和式(40)，变流器直流侧的峰值电流可以表达为：

(42)

从式(42)可以得出，升降系数B不仅与一级匝数比α有关，还和二级匝数比β相关。可以通过两个变压器匝数比来控制升降系数，这是此拓扑结构的独特特性。

4.5 含变压器阻抗源变流器的特点与应用场合

4.1～4.4节介绍了阻抗源网络中含变压器的几种拓扑，除了具有各自独特特点外，该类阻抗源电流型变流器具有如下共同特点：

(1)能够实现单级升降压变换的功能，相比较于电流型Z源和准Z源变流器，其具有更宽的电流升降范围。

(2)阻抗源网络中只包含一个电容元件和变压器，相比较传统的阻抗源网络，减少了元件数量。

(3)只包含一个二极管，可以实现能量功率的双向流动。

电流型Z源和准Z源变流器在升压模式下，输出电压都不能超出其输入电压的2倍，目的是防止二极管的非正常导通，这使其应用范围受到了限制，文献[37]阐述了电流型Trans-Z源变流器在变压器绕组的匝数比n>1时，具有更大的运行操作范围，能够克服上述缺点。当匝数比大于1，除了更宽的操作范围外，电流型Trans-Z源和Trans-准Z源变流器具有更大的电压降压系数。在电动运行状态中当开路矢量状态占空比在0

文献[39]指出电流型Trans-Z源和Trans-准Z源变流器为了达到更高的电流增益，需要更高的变压器匝数比，这使变流器体积增大，成本变高，不利于工业应用，而电流型Flipped-Γ源变流器具有较小的变压器匝数比就可以达到同样的电流增益能力。

文献[40]指出，电流型Flipped-Γ源的升降系数对匝数比较为敏感，需要确定精确的匝数比，这无疑给工业应用带来了额外成本，而电流型Trans-T源变流器具有二极管变压器结构，结合了电流型Trans-Z源和电流型Flipped-Γ源变流器的优点，使电流升降控制变得更加方便、容易。

含变压器阻抗源电流型变流器由于其独特的性能优点，可实现更宽的电压升压范围和双向功率流动，特别适用于需要充电的混合动力汽车中，因为含变压器阻抗源电流型变流器具有良好正弦波形的输出电压和输出电流，可直接耦合马达、发电机和电池；在混合动力汽车中，存在由于电压快速变化产生的电压冲击造成的电机绝缘老化问题、轴漏电流引起的腐蚀造成轴承损耗以及电磁干扰等问题，引入含变压器阻抗源电流型变流器可以避免和解决上述问题。除此之外，含变压器阻抗源电流型变流器可以直接连接到电网，因此不需使用单相120V或三相220V电源提供额外的车载充电器，为新能源汽车和电动汽车提供了一个新型变流器拓扑结构的选择。

5 其他阻抗源电流型变流器

阻抗源网络具有很多种的变形和衍生结构，不同的结构特点适用不同的应用场合，以下简要介绍其他一些电流型阻抗源网络的拓扑结构。

5.1 电流型开关耦合电感变流器

开关耦合变流器是由抽头电感演变而来的，耦合电感的基本作用主要为隔离和电压调节，其拓扑结构如图20所示。

图20 电流型开关耦合电感变流器Fig.20 Current-fed switches coupled converter

在电流型开关耦合电感变流器中，同样地，升降压功能可以通过在变流器工作状态中引入一个额外的开路矢量状态来实现。图21为电流型开关耦合电感变流器的等效电路，其电容数量少且系统尺寸显著降低。此外，相对于传统的升压变流器，它具有较少的开关次数，以及更小的有源器件的电流应力；相比电流型阻抗源变流器，它具有较高的升压比和较低的有源器件电流应力。通过调节升压比率和开路占空比，变流器可以在一些工作区域维持最低的电压和电流应力，升压能力强，成本低，尺寸小，适用于光伏微电网和混合动力汽车充电与电机驱动领域。电流型开关耦合电感变流器具有紧凑、可吸收功率、高效、耐高温、低成本等优点。

图21 电流型开关耦合变流器的两种等效电路Fig.21 Two equivalent circuits of current-fed switches coupled converter

5.2 AC-AC变流器(矩阵变流器)

矩阵变换器是由九个双向功率开关管组合而成，允许输出和输入的任何一相连接，是一种直接的AC-AC变流器，具有良好的正弦波输出波形和可控的输入功率因数。传统矩阵变流器的最大电压增益不超过0.866，另外功率开关易受同相输出端直通或者开路状态的出现而损害器件，而阻抗源型矩阵变流器的出现可以克服这些缺点，其基本拓扑结构如图22所示(其中“X”代表各种双向功率开关管，下同)。在电机拖动类似的交流负载应用中，其优势在于能够自由升降电压和频率。

图22 电流型Z源矩阵变流器Fig.22 Current-fed Z source matrix converter

图23和图24为矩阵变流器与传统阻抗源网络相结合的拓扑结构，矩阵变流器的优点为矩阵变流器输入侧和输出侧的电压和电流均为交流分量，不需要流过直流电流或者直流电压，所以其输入侧的Z源LC网络的成本和尺寸大小比Z源变流器的直流侧网络要小得多。

图23 电流型准Z源矩阵变流器Fig.23 Current-fed quasi-Z source matrix converter

图24 电流型Trans-Z源矩阵变流器Fig.24 Current-fed trans-Z source matrix converter

6 结论

阻抗源电流型变流器以其独有的结构特性和功能特点给传统的电力电子领域提供了一个新的研究方向，可以解决一些传统电流型变流器所不能解决的问题。自从彭方正教授首次提出Z源网络拓扑后，阻抗源网络得到了广泛的关注和研究，阻抗源网络的优越性能体现在能够设计出鲁棒性更好、更通用的变流器拓扑结构，这吸引了学术界和工业界的研究人员和设计师对其进行深入的探索研究。本文内容主要集中在阻抗源电流型变流器的拓扑和工作原理方面，传统的阻抗源网络已经发展到性能更优越的准-Z源网络、Trans-Z源网络和许多其他类型的阻抗源网络拓扑，能够满足特定场合的工业需求，并产生良好的效果。

在全球能源互联化的背景下，如何将各种分布式的新能源并入电网，如何将各种分布式的系统联合起来，以及如何实现未来工业中更复杂精确的指标要求，都对功率变换拓扑结构提出了新的要求，阻抗源电流型变流器由于其独特的性能，已得到广泛的研究和关注，并将逐步应用于工业领域。

[1] 丁新平 (Ding Xinping). Z源变流器关键技术的研究(Research on key aspects in Z-source converter) [D]. 杭州: 浙江大学(Hangzhou: Zhejiang University), 2007.

[2] Peng F Z. Z-source inverter[J]. IEEE Transactions on Industry Applications, 2003, 39(2) : 504-510.

[3] Loh P C, Vilathgamuwa D M, Gajanayake C J, et al. Transient modeling and analysis of pulse-width modulated Z-source inverter[J]. IEEE Transactions on Power Electronics, 2007, 22(2) : 498-507.

[4] Liu J, Hu J, Xu L. Dynamic modeling and analysis of Z source converter - Derivation of AC small signal model and design oriented analysis[J]. IEEE Transactions on Power Electronics, 2007, 22(5): 1786-1796.

[5] Loh P C, Gajanayake C J, Vilathgamuwa D M, et al. Evaluation of resonant damping techniques for Z-source current-type inverter[J]. IEEE Transactions on Power Electronics, 2008, 23(4):2035-2043.

[6] Peng F Z, Shen M S, Qian Z M. Maximum boost control of the Z-source inverter[J]. IEEE Transactions on Power Electronics, 2005, 20(4): 833-838.

[7] Shen M S, Wang J, Joseph A, et al. Constant boost control of the Z-source inverter to minimize current ripple and voltage stress[J]. IEEE Transactions on Industry Applications, 2006, 42(3): 770-778.

[8] Loh P C, Vilathgamuwa D M, Lai Y S, et al. Pulse-width modulation of Z-source inverters[J]. IEEE Transactions on Power Electronics, 2005, 20(6): 1346- 1355.

[9] Loh P C, Blaabjerg F, Wong C P. Comparative evaluation of pulsewidth modulation strategies for Z-source neutral point clamped inverter[J]. IEEE Transactions on Power Electronics, 2007, 22(3): 1005-1013.

[10] 薛必翠, 张承慧, 丁新平(Xue Bicui，Zhang Chenghui，Ding Xinping). Z-源逆变器PWM调制策略的分析与比较(The analysis and comparison of the PWM modulation strategy of the Z-source inverter)[J]. 电工电能新技术(Advanced Technology of Electrical Engineering and Energy), 2013, 32(3): 95-100.

[11] Peng F Z, Joseph A, Wang J, et al. Z-source inverter for motor drives[J]. IEEE Transactions on Power Electronics, 2005, 20(4): 857-863.

[12] Huang Y, Shen M, Peng F Z, et al. Z-source inverter for residential photovoltaic systems[J]. IEEE Transactions on Power Electronics, 2006, 21(6): 1776-1782.

[13] Peng F Z, Shen M, Holland K. Application of Z-source inverter for traction drive of fuel cell-battery hybrid electric vehicles[J]. IEEE Transactions on Power Electronics, 2007, 22(3):1054-1061.

[14] Dehghan S M, Mohamadian M, Yazdian A, et al. Dual-input dual-output Z-source inverter[J]. IEEE Transactions on Power Electronics, 2010, 25(2):360-368.

[15] Loh P C, Gao F, Blaabjerg F, et al. Operational analysis and modulation control of three-level Z-source inverters with enhanced output waveform quality[J]. IEEE Transactions on Power Electronics, 2009, 24(7): 1767-1775.

[16] Loh P C, Gao F, Tan P-C, et al. Three-Level AC-DC-AC Z-Source converter using reduced passive component count[J]. IEEE Transactions on Power Electronics, 2009, 24(7): 1671-1681.

[17] Nguyen M-K, Jung Y-G, Lim Y-C. Single-phase Z-source AC/AC converter with wide range output voltage operation[J]. Journal of Power Electronics, 2009, 9(5): 736-747.

[18] Tang Y, Xie S, Zhang C, et al. Improved Z-source inverter with reduced Z-Source capacitor voltage stress and soft-start capability[J]. IEEE Transactions on Power Electronics, 2009, 24(2): 409-415.

[19] You K, Rahman M F. Analytical model of conduction and switching losses of matrix-Z-source converter[J]. Journal of Power Electronics, 2009, 9(2): 275-287.

[20] Nguyen M-K, Jung Y-G, Lim Y-C, et al. A single-phase Z-source Buck-Boost matrix converter[J]. IEEE Transactions on Power Electronics, 2010, 25(2): 453-462.

[21] Siwakoti Y P, Peng F Z, Blaabjerg F, et al. Impedance-source networks for electric power conversion - Part I: A topological review[J]. IEEE Transactions on Power Electronics, 2015, 30(2): 699-716.

[22] Fang X P, Qian Z M, Qi G, et al. Current mode Z-source inverter-fed ASD system[A]. IEEE 35th Annual Power Electronics Specialists Conference[C]. Aachen, Germany, 2004. 2805-2809.

[23] 房绪鹏(Fang Xupeng). Z源逆变器研究 (Research on Z-source inverter) [D]. 杭州: 浙江大学(Hangzhou: Zhejiang University), 2005.

[24] Thangaprakash S, Krishnan A. Current mode integrated control technique for Z-source inverter fed induction motor drives[J]. Journal of Power Electronics, 2010, 10(3): 285-292.

[25] Lei Q, Yang S T, Peng F Z, et al. Application of current-fed quasi-Z-source inverter for traction drive of hybrid electric vehicles[A]. IEEE Vehicle Power and Propulsion Conference[C]. Dearborn, MI, USA, 2009. 671-677.

[26] Anderson J, Peng F Z. Four Quasi-Z-Source inverters[A]. IEEE Power Electronics Specialists Conference[C]. Rhodes, Greece, 2008. 2743-2749.

[27] Lei Q, Peng F Z, Yang S. Discontinuous operation modes of current-fed Quasi-Z-Source inverter[A]. Twenty-Sixth Annual IEEE Applied Power Electronics Conference and Exposition[C]. Fort Worth, TX, USA, 2011. 437-441.

[28] Yang S, Peng F Z, Lei Q, et al. Current-fed Quasi-Z-Source inverter with voltage Buck-Boost and regeneration capability[J]. IEEE Transactions on Industry Applications, 2011,47(2):882-892.

[29] Lei Q, Cao D, Peng F Z. Novel SVPWM switching pattern for high efficiency 15kW current-fed quasi-Z-source inverter in HEV motor drive application[A]. Twenty Seventh Annual IEEE Applied Power Electronics Conference and Exposition[C]. Orlando, FL, USA, 2012. 2407-2420.

[30] Cao D, Lei Q, Peng F Z. Development of high efficiency current-fed quasi-Z-source inverter for HEV motor drive[A]. 2013 Twenty-Eighth Annual IEEE Applied Power Electronics Conference and Exposition[C]. Long Beach, CA, USA, 2013. 157-164.

[31] Lei Q, Cao D, Peng F Z. Novel loss and harmonic minimized vector modulation for a current-fed quasi-Z-source inverter in HEV motor drive application[J]. IEEE Transactions on Power Electronics, 2014, 29(3): 1344-1357.

[32] Yang S, Peng F Z, Lei Q, et al. Current-fed quasi-Z-source inverter with voltage buck-boost and regeneration capability[A]. IEEE Energy Conversion Congress and Exposition[C]. San Jose, CA, USA, 2009. 3675-3682.

[33] Lei Q. Buck/boost current-source-inverter topologies, modulation and applications in HEV/EV motor drive[D]. East Lansing, USA: Michigan State University, 2012.

[34] Zhu M, Yu K, Luo F L. Switched inductor Z-source inverter[J]. IEEE Transactions on Power Electronics, 2010,25(8): 2150-2158.

[35] Nguyen M K, Lim Y C, Cho G B. Switched-inductor quasi-Z-source inverter[J]. IEEE Transactions on Power Electronics, 2011, 26(11): 3183-3191.

[36] Li D, Gao F, Loh P C, et al. Hybrid-source impedance networks: Layouts and generalized cascading concepts[J]. IEEE Transactions on Power Electronics, 2011, 26(7): 2028-2040.

[37] Qian W, Peng F Z, Cha H. Trans-Z-source inverters[J]. IEEE Transactions on Power Electronics, 2011, 26(12): 3453-3463.

[38] Strzelecki R, Adamowicz M, Strzelecka N, et al. New type T-source inverter[A].Compatibility and Power Electronics International Conference[C]. Badajoz, Spain, 2009. 191-195.

[39] Poh Chiang L, Ding L, Blaabjerg F. Current type flipped-Γ-source inverters[A]. IEEE Power Electronics and Motion Control Conference [C]. Harbin, China, 2012. 594-598.

[40] Quang-Vinh T, Kay-Soon L. A new current-type magnetically coupled T-source inverter[A]. IEEE International Industrial Technology Conference[C]. Busan, South Korea, 2014. 318-323.

Basic principle and research status of impedance source current-fed converter

LI Da-fei1,2,3， GUO Wen-yong1,3， QUAN Sheng-cai1,2,3

(1. Institute of Electrical Engineering, Chinese Academy of Sciences, Beijing 100190, China; 2. University of Chinese Academy of Sciences，Beijing 100049, China; 3. Key Laboratory of Applied Superconductivity, Chinese Academy of Sciences, Beijing 100190, China)

Due to its unique boost and buck function, impedance source topology is getting more and more attention and has been applied in electric power conversion circuit. Various converter topologies have been reported in the literature to overcome the limitations and problems of the traditional converter topologies. Proper implementation of the impedance-source network with appropriate switching congurations and topologies reduces the number of power conversion stages in the power system, which may improve the reliability and performance of the power system. The impedance source converter can be generally classified into voltage-fed and current-fed types. Compared to the voltage-fed type, current source converter has the advantages of faster dynamic response, stronger current limiting capability, bigger dc circuit impedance, and higher input voltage. This paper provides a comprehensive review of the various impedance-source-networks-based current-fed power converters, summarizes the development history and current research status of impedance source current fed converter, and analyzes the topology and its advantages of the representative impedance source current source inverter and gives an outlook of its future development.

impedance source; current-fed; buck-boost

2015-11-16

国家自然科学基金项目(50907070；51361135705)、 国家863计划项目(2013AA050803)

李大飞(1991-)， 男， 安徽籍， 硕士研究生， 研究方向为电力电子及其控制； 郭文勇(1979-)， 男， 福建籍， 副研究员/硕导， 博士， 研究方向为新能源发电、 储能技术、 故障限流器和电力电子技术(通信作者)。

TM401

A

1003-3076(2016)08-0046-11