基于自适应滑模观测器的永磁同步电机无位置传感器控制

陈 炜， 张志伟

(天津大学电气与自动化工程学院， 天津 300072)

基于自适应滑模观测器的永磁同步电机无位置传感器控制

陈 炜， 张志伟

(天津大学电气与自动化工程学院， 天津 300072)

为了实现永磁同步电机的无位置传感器控制，本文提出了一种自适应滑模观测器。该观测器通过一种李雅普诺夫函数来获取反电动势的估计方程，然后基于估计反电动势计算出转子位置。基于反电动势模型建立速度观测器，应用模型参考自适应方法，实现对电机转速的估计。仿真和实验结果表明，本文所提出的方法能够实现对转子位置和电机转速的准确估计，具有较好的动静态性能，可以改善低速下转子位置和电机转速的估计效果。

永磁同步电机； 无位置传感器控制； 反电动势； 滑模观测器

1 引言

永磁同步电机由于具有高效率、高功率密度和过载能力强等优点被广泛应用于工业领域。为了达到对高性能永磁同步电机精确控制的目的，工业的控制中常采用高精度位置传感器，其性能直接影响电机系统运行稳定性。一旦位置传感器故障或者其输出的转子位置信号失准，就会导致控制失败。从这个角度来看，利用控制算法实现对转子位置估计将成为降低永磁同步电机控制系统风险的一个有效的后备解决方案。事实上，利用控制算法实现对永磁同步电机转子位置检测的方法，即无位置传感器控制方法，已经成为重要的研究方向[1,2]。

无位置传感器控制方法主要分为两大类：观测器法和高频信号注入法。观测器法是将电机的电压、电流作为观测器输入，利用控制算法估计转子位置，主要包括模型参考自适应法[3]、扩展卡尔曼滤波器法[4]、滑模观测器法[5]等。其中，扩展卡尔曼滤波器法和模型参考自适应法在一定程度上依赖于电机模型，模型的准确性将决定转子位置的估计精度。高频信号注入法是根据电机凸极效应，通过外加高频激励，实现对转子位置的检测。该方法适用于电机低速运行，对信号检测精度要求较高，且需要设计多个滤波器，实现起来比较复杂，同时高频激励的注入会给系统带来噪声，降低系统性能。

相比其他方法，滑模观测器具有对扰动鲁棒性强、对模型参数变化敏感性低和算法简单等优点，在一定程度上解决了系统参数变化、扰动等带来的影响。然而由于传统滑模观测器中符号函数的离散开关特性容易导致估计反电动势中存在高频抖振，文献[6,7]采用sigmoid函数和饱和函数代替符号函数来估计反电动势，有效削弱了反电动势中的高频抖振。

本文将滑模变结构控制与自适应控制相结合，提出了一种自适应滑模观测器，基于李雅普诺夫稳定性理论对观测器的稳定性进行了分析并求解出反电动势的估计方程，实现对反电动势的估计，计算出转子位置。建立基于反电动势模型的速度观测器，应用模型参考自适应方法，实现对电机转速的估计。最后通过仿真和实验验证了该方法的有效性。

2 永磁同步电机无位置传感器控制

2.1 基于自适应滑模观测器的转子位置估计

永磁同步电机在静止α-β坐标系下的数学模型为：

(1)

式中，iα、iβ分别为定子电流α-β轴分量；uα、uβ分别为定子电压α-β轴分量；eα、eβ分别为反电动势α-β轴分量；Ls和Rs分别为定子电感和定子电阻；ψf为永磁体磁链；ωe为电机电角速度；θe为以电角度表示的转子位置角。

选取滑模面为：

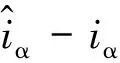
(2)

传统滑模观测器采用bang-bang控制获取等效反电动势，bang-bang控制为不连续控制，反电动势中伴随高频抖振分量。因此本文采用光滑连续的sigmoid函数来构建自适应滑模观测器，该sigmoid函数为：

(3)

式中，a为一个正实数。

构建自适应滑模观测器如下：

(4)

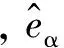
将式(4)与式(1)中的电流方程作差可得电流误差方程为：

(5)

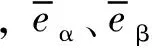
为使自适应滑模观测器稳定，同时为获取反电动势的估计方程，定义李雅普诺夫函数为：

(6)

式中，η为正系数。

对式(6)求导，可得：

(7)

在一个控制周期内反电动势缓慢变化，把它看作为常数，将式(5)代入式(7)中，可得：

(8)

为使观测器稳定，需保证

(9)

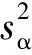
(10)

(11)

根据以上分析，图1给出了自适应滑模观测器的结构框图。

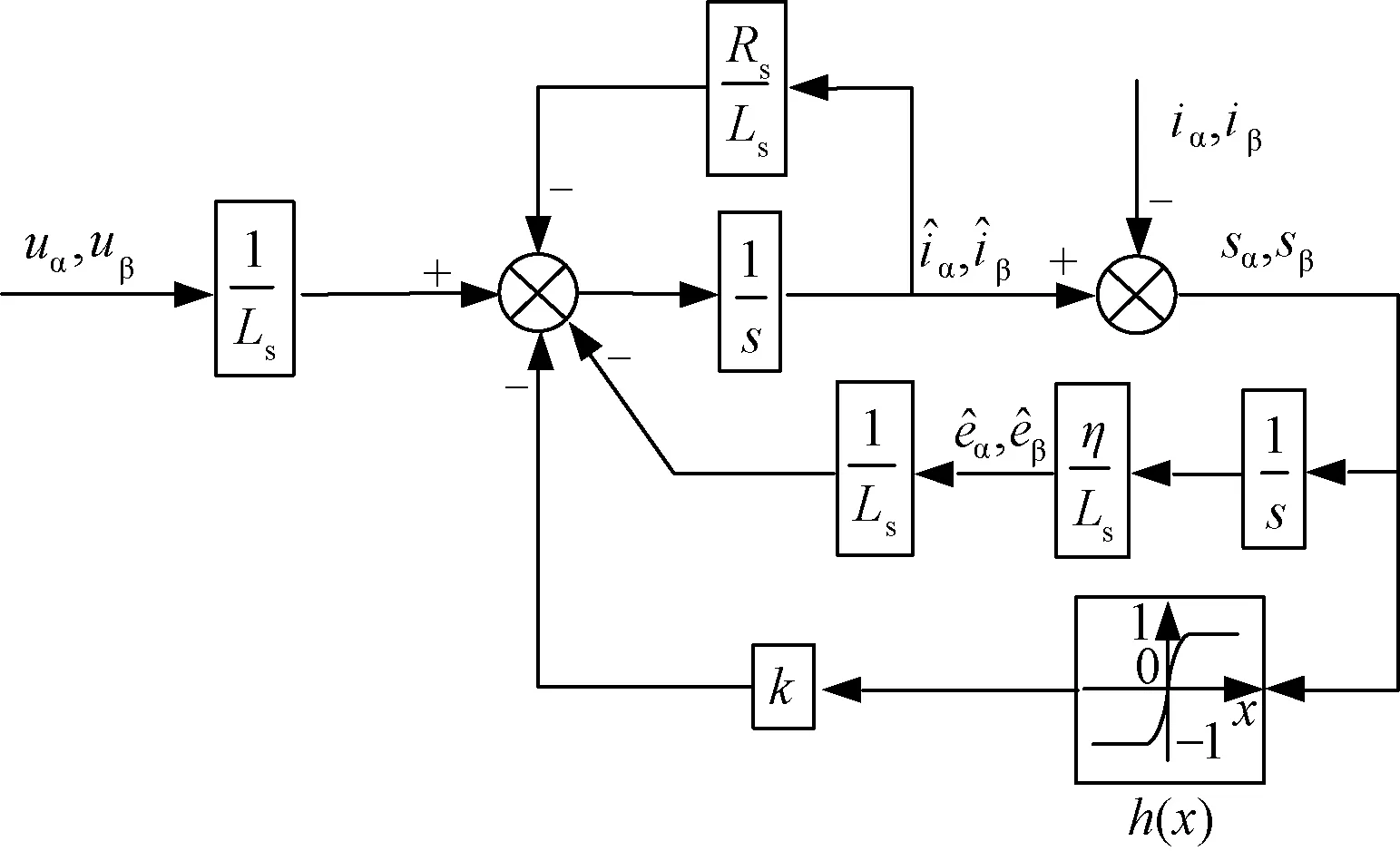
图1 自适应滑模观测器结构框图Fig.1 Block diagram of adaptive sliding mode observer

2.2 基于模型参考自适应原理的电机转速估计

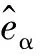
(12)

根据式(12)建立速度观测器为：

(13)

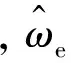
将式(13)与式(12)作差，进一步得到反电动势误差方程为：

(14)

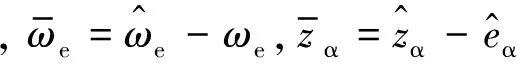
为求解电机转速的自适应律，根据李雅普诺夫稳定性理论，定义李雅普诺夫函数为：

(15)

对式(15)求导，可得：

(16)

将式(14)代入式(16)，则有

(17)

式(17)中右端第一项总是为负值，只要第二项和第三项之和为零，就可保证dV2/dt负定，由此可得转速的自适应律：

(18)

为改进速度的动态响应，将式(18)修正为：

(19)

基于以上对电机转速估计方法的分析，图2给出了基于模型参考自适应法的转速估计框图。

图2 基于模型参考自适应法的估计电机转速框图Fig.2 Block diagram of estimated motor speed based on MRAS

2.3 永磁同步电机无位置传感器控制系统

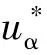
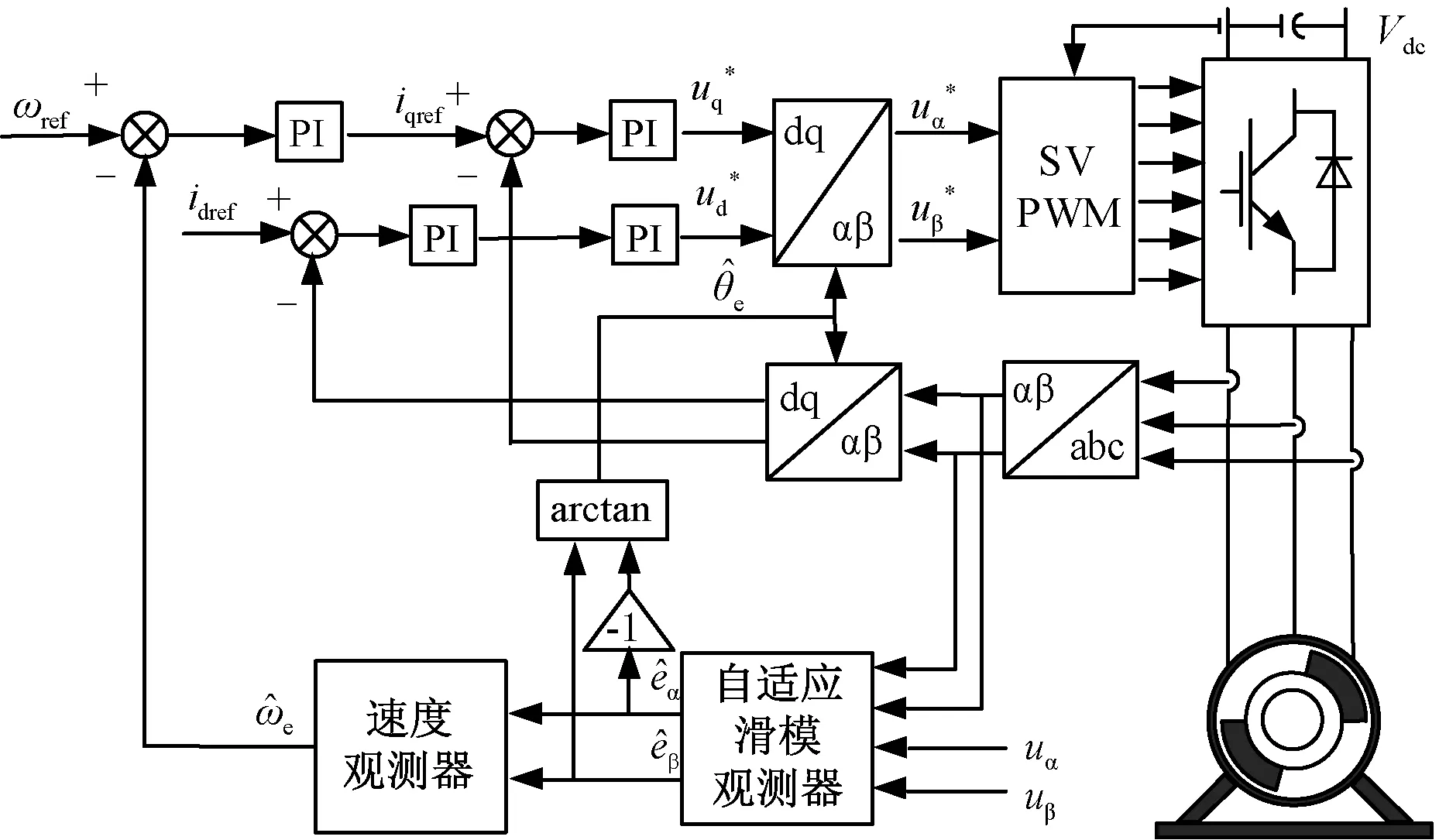
图3 永磁同步电机无位置传感器矢量控制系统框图Fig.3 Block diagram of sensorless PMSM vector control system

3 实验结果与分析

3.1 仿真结果分析

为验证本文提出方法的有效性，利用Matlab/Simulink建立仿真模型，对比分析了基于bang-bang控制的传统滑模观测器的无位置传感器控制方法和本文提出的方法，仿真中被控电机参数如表1所示。

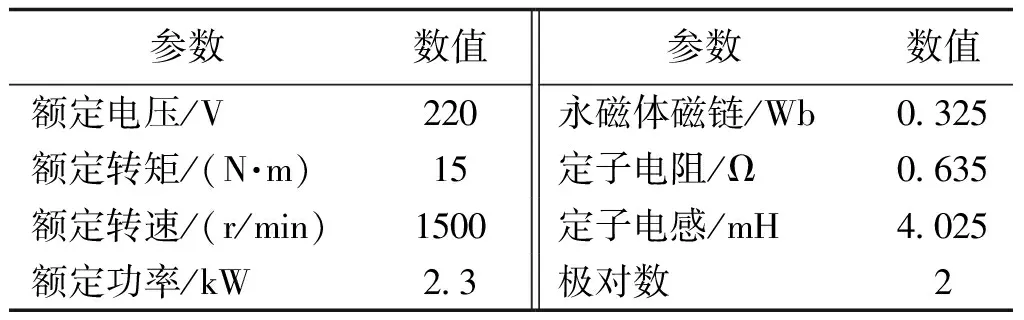
表1 电机参数Tab.1 Parameters of tested motor

图4给出了给定转速分别为ωr=100r/min和ωr=1500r/min下的估计反电动势及其局部的波形。可以看出，在不同给定转速下基于bang-bang控制的传统方法获得的估计反电动势存在不同程度的高频抖振，基于本文方法得到的估计反电动势波形较为平滑。

图4 估计反电动势及其局部的波形Fig.4 Waveforms of estimation of back-emf and its local amplification

图5给出了给定转速分别为ωr=100r/min和ωr=1500r/min下的估计转子位置及其局部波形。可以看出，在低速ωr=100r/min下基于bang-bang控制的传统方法得到的转子位置受高频抖振影响很大，估计转子位置中存在大量毛刺，高速下估计转子位置中的毛刺明显减少。在不同给定转速下基于本文方法得到的估计转子位置波形都较为光滑，基本不含高频抖振。

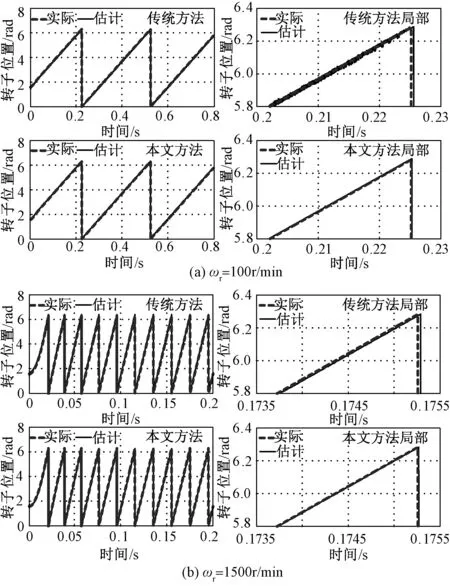
图5 估计转子位置及其局部的波形Fig.5 Waveforms of estimation of rotor position and its local amplification

图6给出了给定转速分别为ωr=100r/min和ωr=1500r/min下基于反电动势和永磁体磁链实现对电机转速估计的传统方法和本文方法的估计电机转速及其局部的波形。可以看出，与基于反电动势和永磁体磁链实现对电机转速估算的传统方法相比，基于本文方法得到的电机转速响应较慢一些，但得到的电机转速比较平滑，几乎不含高频抖振分量。

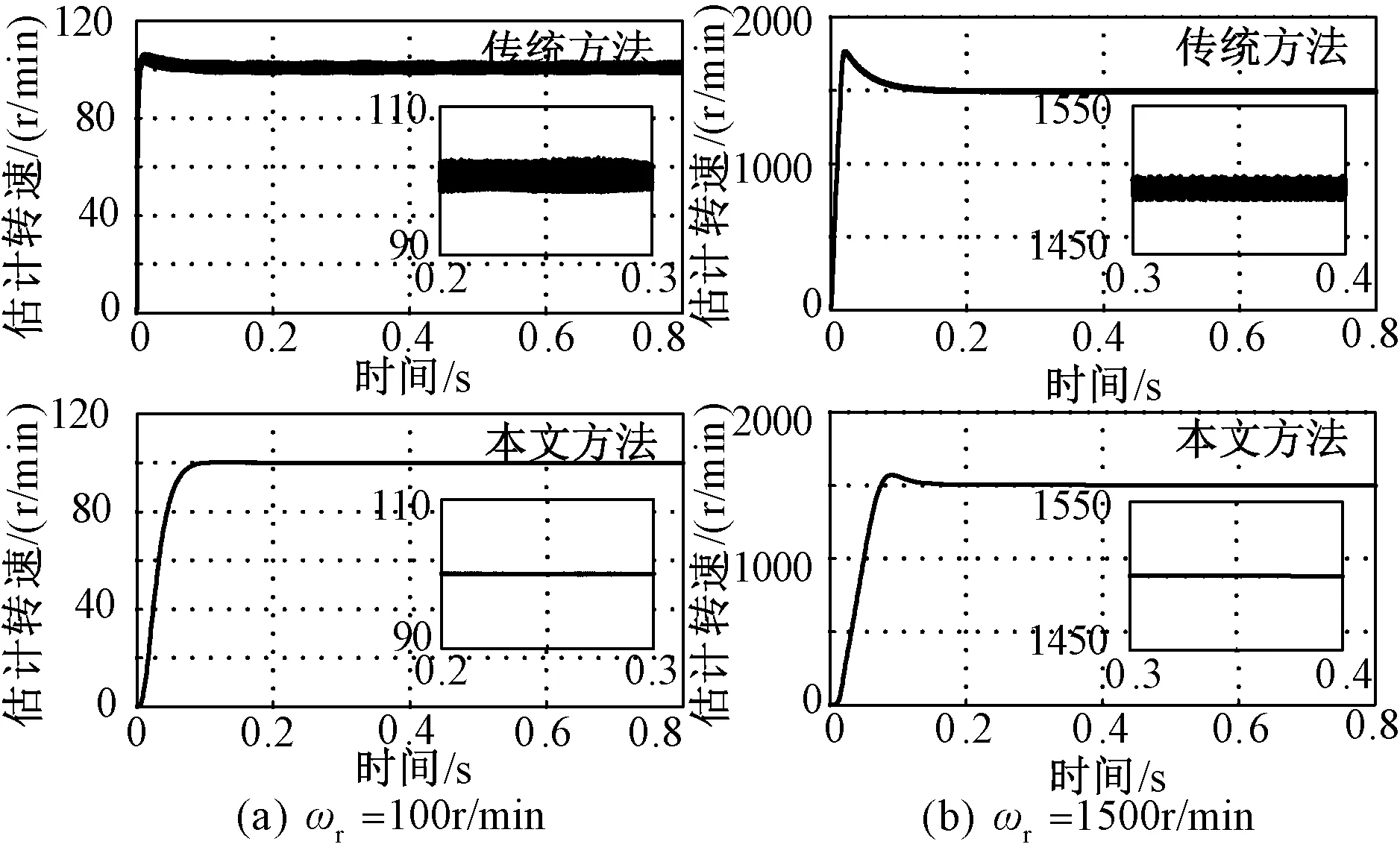
图6 估计电机转速及其局部的波形Fig.6 Waveforms of estimation of motor speed and its local amplification

3.2 实验结果分析

为验证本文所提出方法的有效性，采用永磁同步电机矢量控制系统来进行实验验证。实验系统中功率器件采用IPM模块PS21867，开关频率5kHz，控制芯片采用TI公司的TMS320F28335型DSP，系统采样周期为200μs，电机主要参数如表1所示，实验系统如图7所示。

图7 永磁同步电机实验平台Fig.7 PMSM experimental platform

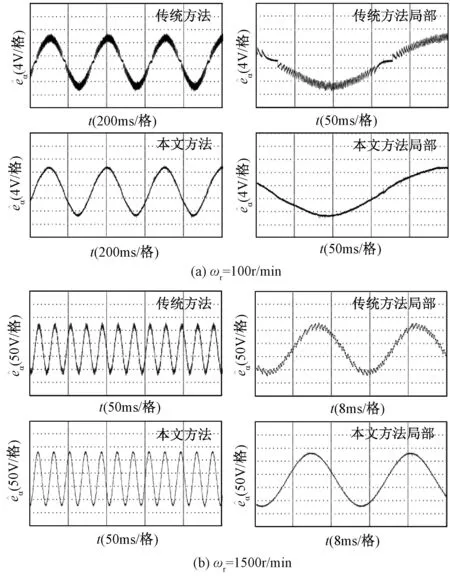
图8 估计反电动势及其局部的实验波形Fig.8 Experimental waveforms for estimation of back-emf and its local amplification

图8给出了给定转速分别为ωr=100r/min和ωr=1500r/min下的估计反电动势及其局部的实验波形。可以看出，在不同转速下基于传统方法得到的估计反电动势存在不同程度的高频抖振，基于本文方法得到的估计反电动势波形较为光滑，基本不含有高频抖振分量。

图9给出了给定转速分别为ωr=100r/min和ωr=1500r/min下的估计转子位置及其局部的实验波形。可以看出，受估计反电动势中高频抖振的影响，基于传统方法得到的估计转子位置存在不同程度的高频抖振，尤其在低速ωr=100r/min下高频抖振尤为明显。而在不同转速下基于本文方法得到的估计转子位置波形都比较光滑，基本不含有高频抖振分量。

图10给出了给定转速分别为ωr=100r/min和ωr=1500r/min下基于传统转速估计方法和本文方法的估计电机转速的实验波形。图11～图13分别为给定转速ωr=400r/min变化到ωr=600r/min时传统方法和本文方法得到的估计反电动势、估计转子位置和估计电机转速的实验波形。

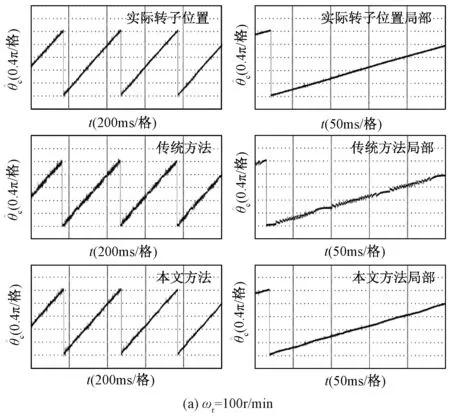
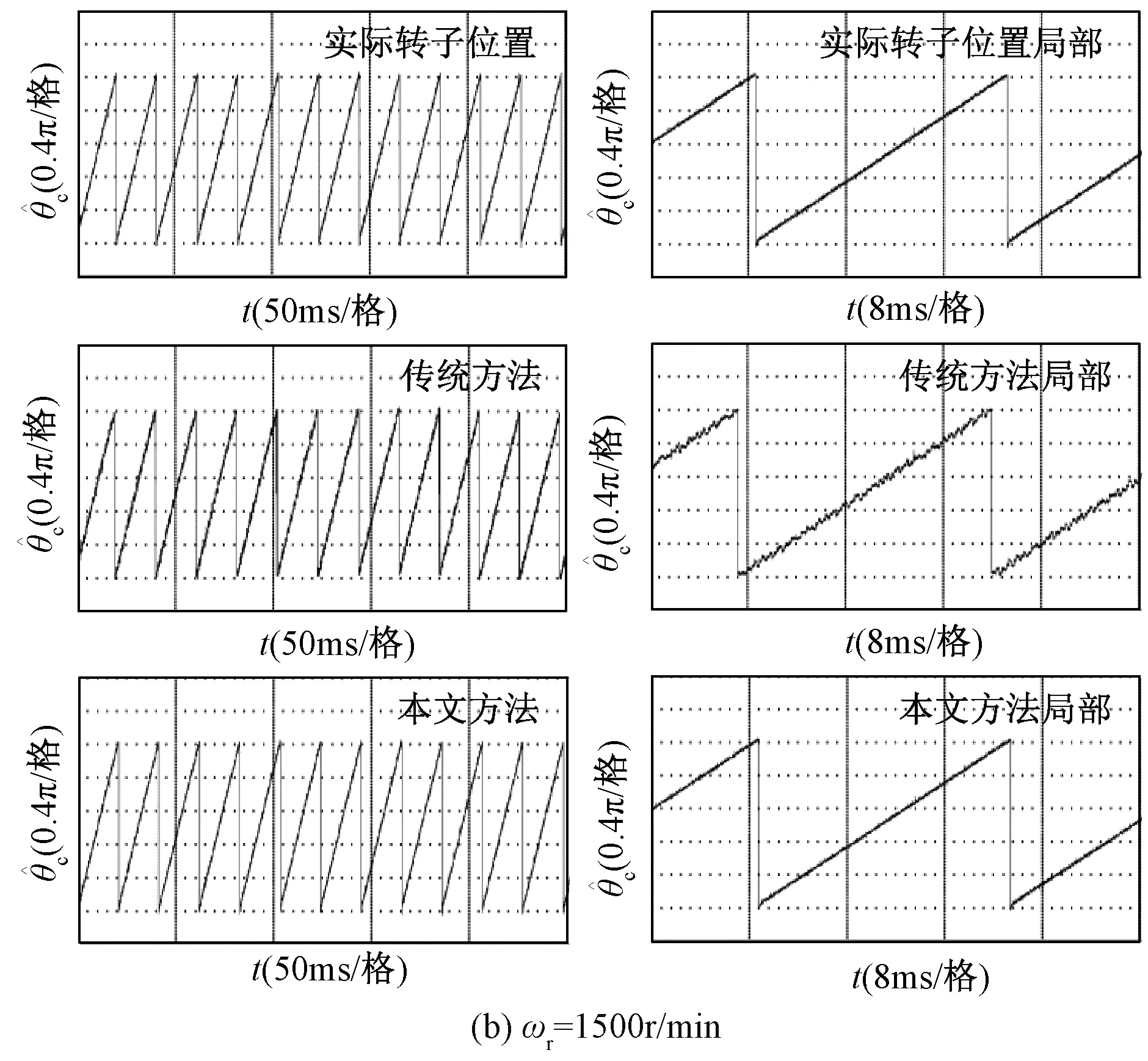
图9 估计转子位置及其局部的实验波形Fig.9 Experimental waveforms for estimation of rotor position and its local amplification

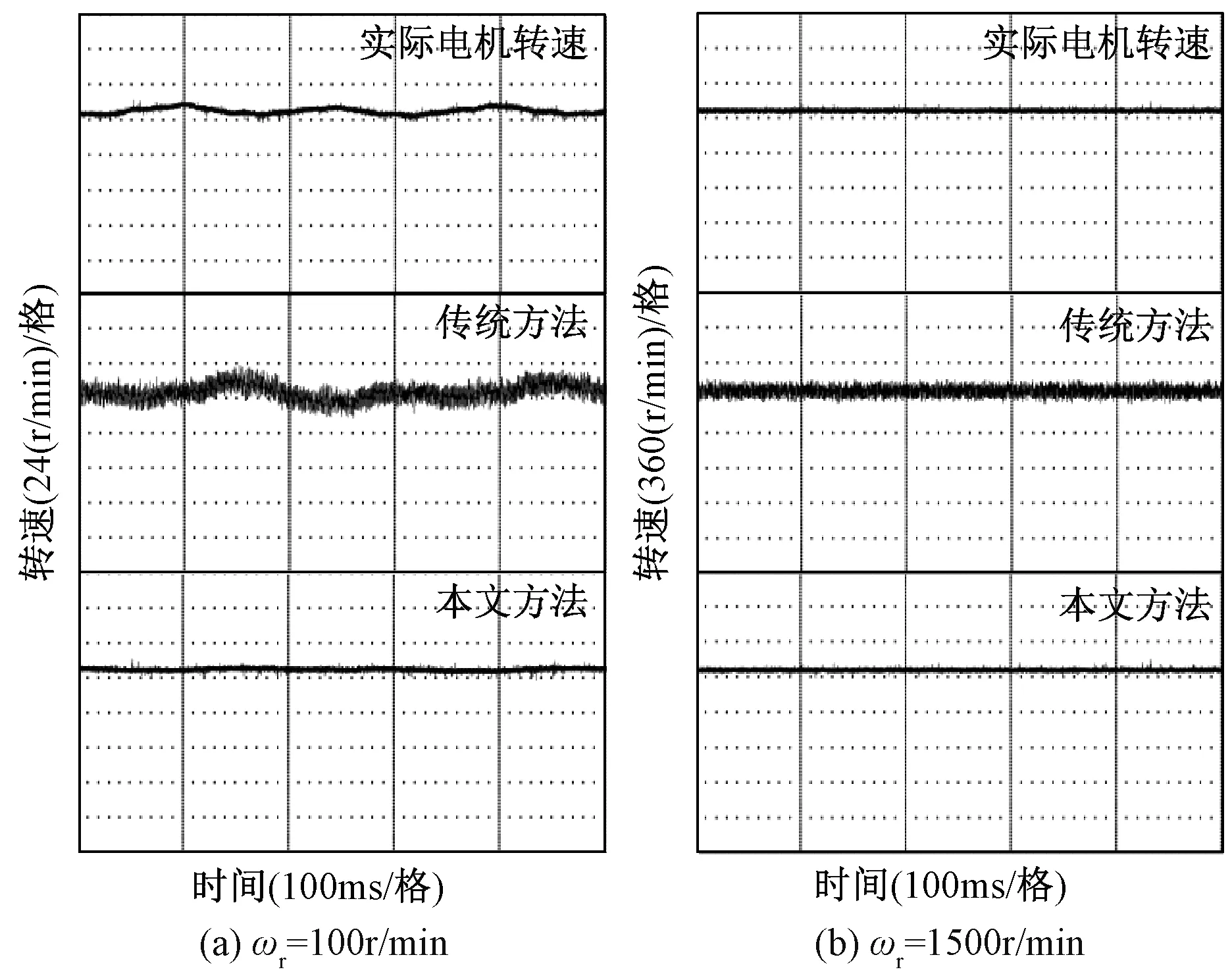
图10 估计电机转速的实验波形Fig.10 Experimental waveforms for estimation of motor speed

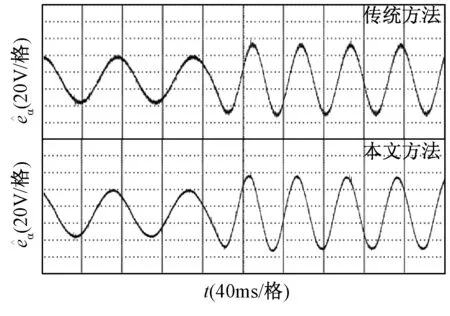
图11 估计反电动势的实验波形Fig.11 Experimental waveforms for estimation of back emf

图12 估计转子位置的实验波形Fig.12 Experimental waveforms for estimation of rotor position

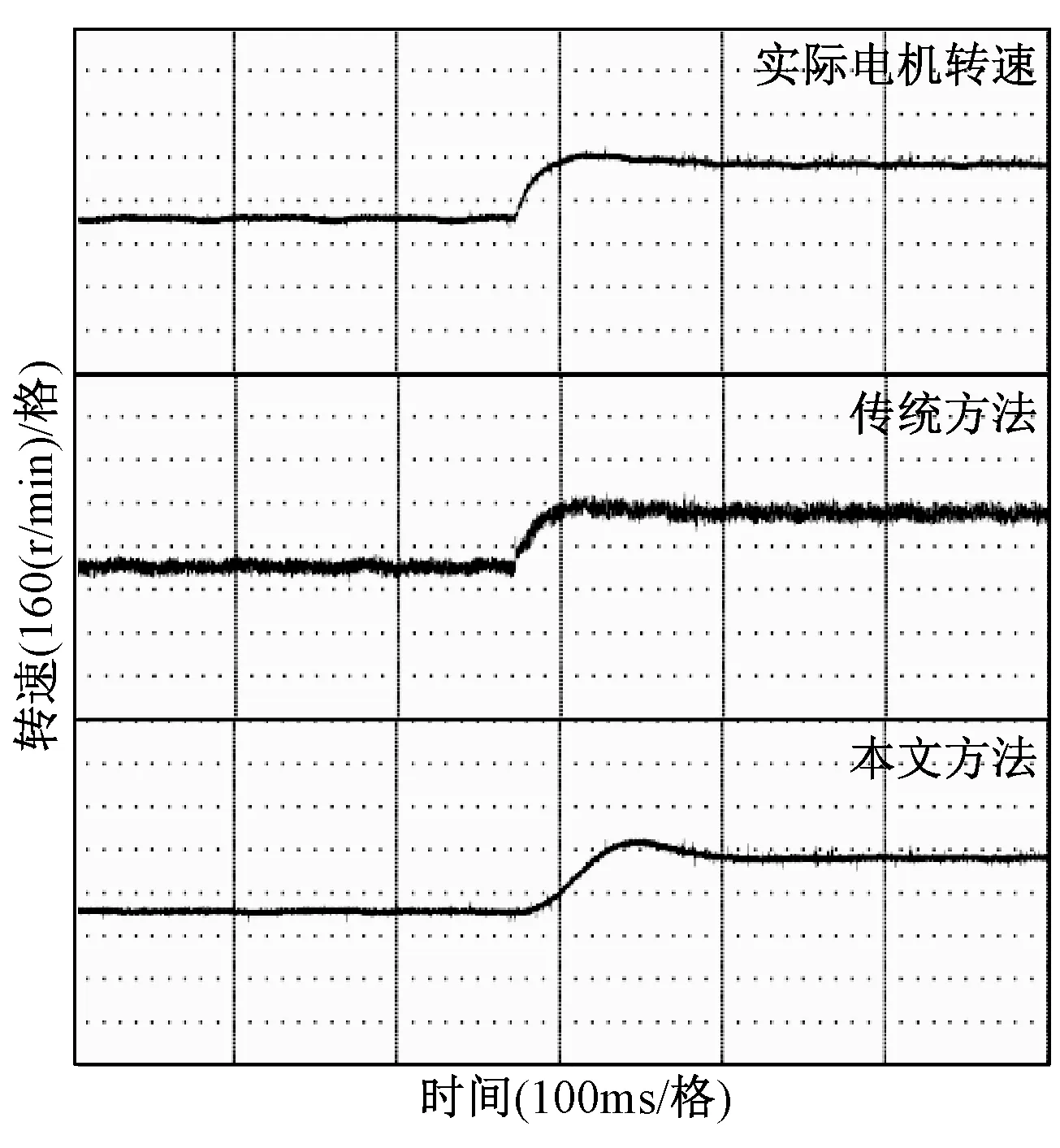
图13 估计电机转速的实验波形Fig.13 Experimental waveforms for estimation of motor speed

由图10可以看出，在不同给定转速下基于传统方法得到的估计电机转速均呈现出高频抖振，而基于本文方法得到的估计电机转速比较光滑，基本不含有高频抖振。图11～图13进一步验证本文方法的正确性。

由图11～图13可以看出，当给定转速变化后，基于传统方法获得的估计反电动势、估计转子位置和估计电机转速都出现一定程度的抖振，而采用本文方法能较为准确地估计反电动势、转子位置和电机转速，并且观测波形比较光滑。

4 结论

本文提出了一种基于自适应滑模观测器的永磁同步电机无位置传感器控制的新方法，该方法能够很好地解决传统方法估计出的反电动势、转子位置和电机转速存在高频抖振的问题，并且具有较好的低速性能，能够在较低速度区域很好地跟踪实际转子位置和实际转速。仿真和实验结果验证了本文提出方法的有效性。

[1] Bolognani S, Calligaro S, Petrella R, et al. Sensorless control of IPM motors in the low-speed range and at standstill by HF injection and DFT processing[J]. IEEE Transactions on Industry Applications, 2011, 47(1): 96-104.

[2] 夏长亮，方红伟(Xia Changliang, Fang Hongwei)．永磁无刷直流电机及其控制(Permanent-magnet brushless DC motor and its control)[J]．电工技术学报(Transactions of China Electrotechnical Society)，2012，27(3)：25-34．

[3] T O Kowalska, M Dybkowski. Stator-current-based MRAS estimator for a wide range speed-sensorless induction-motor drive[J]. IEEE Transactions on Industrial Electronics, 2010, 57(4): 1296-1308.

[4] S Bolognani, R Oboe, M Ziglitto. Sensorless full-digital PMSM drive with EKF estimation of speed and rotor positon[J]. IEEE Transactions on Industrial Electronics, 1999, 46(1): 184-191.

[5] 王高林，张国强，贵献国，等(Wang Gaolin, Zhang Guoqiang, Gui Xianguo, et al.)．永磁同步电机无位置传感器混合控制策略(Hybrid sensorless control strategy for permanent magnet synchronous motors)[J]．中国电机工程学报(Proceedings of the CSEE)，2012，32(24)：103-109．

[6] J Kim, J Son, J Lee. A high-speed sliding-mode observer for the sensorless speed control of a PMSM[J]. IEEE Transactions on Industrial Electronics, 2011, 58(9): 4069-4077.

[7] 鲁文其，胡育文，杜栩杨，等(Lu Wenqi, Hu Yuwen, Du Xuyang, et al.)．永磁同步电机新型滑模观测器无传感器矢量控制调速系统(Sensorless vector control using a novel sliding mode observer for PMSM speed control system)[J]．中国电机工程学报(Proceedings of the CSEE)，2010，30(33)：78-83．

A position sensorless control strategy for PMSM based on
adaptive sliding mode observer

CHEN Wei，ZHANG Zhi-wei

(School of Electrical Engineering and Automation, Tianjin University, Tianjin 300072, China)

In order to realize sensorless control of permanent magnet synchronous motor (PMSM), this paper proposed an adaptive sliding mode observer. By using a Lyapunov function, the equations of the back electromotive force are derived. In this way, even without the low-pass filters and phase compensation module in this control system, the smooth back electromotive force signals can be obtained. Then the rotor position is calculated by the estimation of back electromotive force. Based on the back electromotive force model a velocity observer is designed. At last, the rotor velocity is estimated by using the model reference adaptive algorithm. The experiments with a 1500 r/min prototype of permanent magnet synchronous motor are carried out. The simulation and experimental results show that the proposed method can accurately estimate the rotor position and rotor velocity，and has better dynamic and static performance, which can improve the estimation performance of the rotor position and rotor velocity at low speed.

permanent magnet synchronous motor; position sensorless control; back electromotive force; sliding mode observer

2015-11-03

国家自然科学基金项目 (51577126)、天津市科技支撑计划项目(16YFZCSF00580)

陈 炜(1977-)， 男， 山西籍， 副教授， 博士， 主要研究方向为电机系统及其控制； 张志伟(1990-)， 男， 河北籍， 硕士研究生， 主要研究方向为电机系统及其控制。

TM351

A

1003-3076(2016)08-0008-07