微话题研讨：寻找素材，追求和谐*——以“平行线分线段成比例的基本事实”的探究为例

2016-05-03江苏省南通市陈桥中学陈建均

中学数学杂志 2016年6期

☉江苏省南通市陈桥中学　陈建均

☉江苏省南通市陈桥中学陈建均

义务教育数学课程标准（2011年版）要求“掌握基本事实：两条直线被一组平行线所截，所得的对应线段成比例.”在近期的课题组活动中，围绕这一基本事实的教学，我们进行了专题研讨，在研讨的基础上安排了研究课，收获非常多.在此笔者分享部分专题研讨内容、教学片断和几点反思，以期得到更多同行的指导.

一、专题研讨

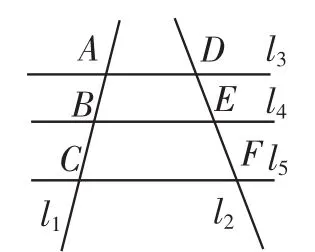
图1

话题一：教材如何处理？

探究：（人教版九年级下册第29页）如图1，任意画两条直线l1，l2，再画三条与l1，l2都相交的平行线l3，l4，l5.分别度量l3，l4，l5在l1上截得的两条线段AB，BC和在l2上截得的两条线段DE，EF的长度，与相等吗？任意平移l5，还相等吗？

可以发现，当l3∥l4∥l5时，有

一般地，我们有平行线分线段成比例的基本事实：两条直线被一组平行线所截，所得的对应线段成比例.

话题二：对于教材的探究设计，教学参考书怎样解释？

由于证明涉及无理数等知识，学生尚不能理解，而且引入这个基本事实的目的是得到判定三角形相似的结论.教材没有给出证明，而是设置了探究栏目，引导学生度量相关的线段长度，从而发现规律.

度量会产生误差，因此实际计算得到的结果不一定相等.

话题四：新课标提出教师要引导学生学会质疑，培养严谨的数学精神.这是一个教学严谨的探究吗？

我们想到了关于“三角形内角和定理”的学习.学生在小学先度量进行猜想，再实验操作（拼成一个平角）进行验证；在初中运用平行线的性质进行证明.这个例子很好地体现了数学是一门追求严谨的科学，小学发展学生的具象思维（即直观观察，动手操作），初中以此为基础发展学生的抽象逻辑思维.教材多次测量得出的结论真实可靠吗？最多也就是一个不完全归纳，何况每一次计算的结果还存在误差，这不是一个严谨的探究.

话题五：学生用现有的知识真的无法证明吗？

可以证明，下面是百度百科中的证明方法：如图2，连接AE、BD、BF、CE，根据平行线的性质可得S△ABE=S△BDE， S△BCE=S△BEF，所以，根据不同底等高三角形面积比等于底之比可得

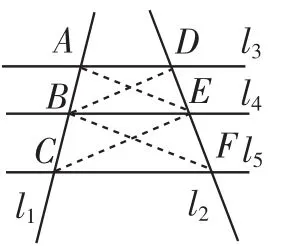
图2

话题六：大家平时怎么教？

有三种处理方式：方式一，沿用老教材的教法，作为平行线分线段成比例定理讲；方式二，照本宣科，教师告诉学生结果是相等的，度量的误差导致了计算结果的误差，学生默认了这一基本事实，不再深究；方式三，分两个阶段教，八年级中位线部分补充教平行线等分线段定理，九年级教平行线分线段成比例定理.

我们认为采用方式一教学的教师没有注意研究课标和教材的变化；采用方式二教学的教师仍然是一言堂，学生习惯性地屈从了教材和教师；采用方式三教学的教师让学生错过了运用探究平行线等分线段定理的经验研究平分线分线段成比例定理的机会.

话题七：学生已经学过平行线、全等三角形等平面几何知识.如何对教材的探究活动进行优化，一方面让学生的探究“有迹可循”；另一方面又不失数学的严谨性呢？

三条平行线，我们认为可以按相邻两条平行线间的距离是否相等分为两类：等距和不等距.在研究的顺序上，先研究等距，再研究不等距，体现特殊到一般的研究思想；在研究的思路上，先猜想，再证明.

我们的探究方案有如下两种：

探究1：如图3，直线l3，l4，l5相互平行，且l3，l4，l5之间的距离相等，直线l1，l2与直线l3，l4，l5分别相交于点A，B，C， D，E，F.相等吗？请说明理由.

探究2：如图4，直线l3，l4，l5相互平行，且l3，l4，l5之间的距离不相等，直线l1，l2与直线l3，l4，l5分别相交于点A，B， C，D，E，F.还相等吗？请说明理由.

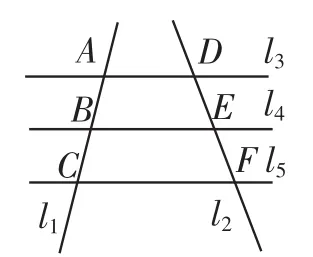
图3

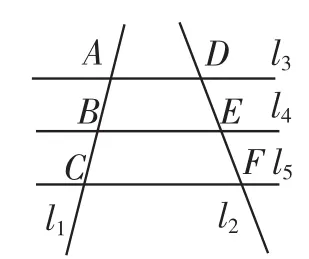
图4

教学预设：探究1，学生通过度量发现AB=BC，DE= EF.证明线段相等，学生自然联想到构建全等三角形.教师启发学生不构建全等三角形，还有没有其他证明方法？探究2，学生会发现此时构建全等三角形的环境遭到了破坏，运用面积成为自然的选择.在完成两个探究后，教师再追问直线l1和l2上的线段，还能写出哪些类似于的结论？说说为什么？最后揭示文字内容.

（为了检验我们的研讨成果，同时掌握学生真实的反馈情况，笔者提议下午上研究课）

二、教学片断

师：同学们，今天我们运用前面所学的知识上一节数学活动课.

师：探究1的结论成立吗？如何证明呢？（让学生独立思考了一段时间）

生1：结论成立，如图5，过点A作AG⊥l4于点G，过点B作BH⊥l5于点H，由题意可知AG=BH，易证△ABG≌△BCH，AB=BC，同理可证DE=EF，所以

图5

图6

（其他类似构建全等三角形的方法不再赘述）

师：如果不构建全等三角形，还有其他证明方法吗？

生2：还可以连接AE，CE，如图6，△ABE和△BCE都以BE作为底，由题意可知（l3，l4，l5之间的距离相等），△ABE和△BCE的面积相等，所以AB=BC.连接BD，BF，同理可证DE=EF.

师：说说你怎么想的？

生2：如果AB=BC，BE是△ACE的中线，那么△ABE和△BCE的面积相等；反之，如果△ABE和△BCE的面积相等，那么AB=BC.

生3：选择BE作为底，根据平行线间的距离相等，可知△ABE和△BDE的面积相等，△BCE和△BEF的面积相等.

师：探究1中l3，l4，l5之间的距离相等属于特殊情况，那么l3，l4，l5之间的距离不相等，上述结论还成立吗？请同学们继续探究.

生4：成立.

师：怎么证明？

生4：假设l3与l4之间距离为m，l4与l5之间距离为n，则，同理，所以结论成立.生5：我们还可以借鉴前面的方法，，则

师：看来无论l3，l4，l5之间的距离是否相等，始终成立.观察直线l1和l2上的线段，你还能写出哪些类似于的结论？说说为什么？

……

师：同学们已经总结出了一般规律，并分别用图形语言和几何语言进行了描述，下面我们一起给出文字语言.

（整个过程大约二十分钟）

三、几点思考

1.微话题探讨，旨在寻找合适的学习素材

我们认为教师在进行教学设计的时候，不能盲从，要注意研读教材、课标和教学参考书，要基于知识前后的内在联系和学情，进行学材再结构.在研读了课标和教学参考书后，我们明白了教材编排的用意，作为基本事实，作为过程性工具.但是仅仅用度量发现结论，看似学生都记住了，掌握了，其实对于发展学生的思维能力并没有什么帮助.所以在集体备课之初，笔者作为课题主持人将微话题探讨的定位放在：如何体现知识前后的内在联系，为学生找到合适的学习素材？让学生原有的知识不仅作为解决问题的依据，而且还要作为发展新知识的起点.在探讨的过程中，我们的研究思路更加明晰：研究的方法上体现特殊到一般的关系；从呈现的方式上改为先判断，再证明，度量猜想隐含其中，目标指向更明确；在归纳方式上体现数学学习就是数学语言的学习，从图形语言到几何语言，再到文字语言；在学习的方式上先独立思考，再交流展示，教师追问，相互启发，逐步完善，最终实现学生的自主建构.

2.微话题探讨，旨在追求和谐的数学学习

我们认为和谐的数学学习追求内在的自然.教材要求学生先度量线段的长度，判断比值是否相等；再平移直线l5，再度量，再判断.我们认为此处学生完全听从教材的安排在跟着做，完全不需要思考，更谈不上活动经验的积累.改编之后的探究要求先判断，再证明.我们注意到学生进行判断时，自然调用了原有的经验，选择度量进行初步的判断.在度量过程中，学生发现线段相等，为下一步证明提供了线索.用全等三角形证明线段相等是最常见的方法，因此，笔者进行了追问“如果不构建全等三角形，还有其他证明方法吗？”我们课前的设想仍然是方法二，我们认为学生联想到中线再运用面积进行证明的方法更自然，也为方法二提供了研究的图形基础，在后面不等距的探究中成果进一步扩大，教师顺势而为，学习过程更加和谐.整个探究过程仅用了二十分钟，为学生的智慧点赞.