拉长思维过程 内化概念理解
2016-05-03福建省三明市列东中学詹高晟
☉福建省三明市列东中学 詹高晟
拉长思维过程内化概念理解
☉福建省三明市列东中学詹高晟
数学概念是数学学习的起点,是数学思维的基础.正确理解概念是学生掌握数学基础知识的前提,也是掌握数学基本技能、提高解题能力的必要条件,可见概念教学在数学教学中占有非常重要的地位.然而,由于很多数学概念具有高度的概括性,对于初中学生来讲显得比较抽象,不易理解,这就要求教师在教学时,要准确把握学生的认知水平,放慢教学节奏,引导学生经历概念的形成与建构,促进对概念本质的理解.最近,笔者通过网络平台观摩了两位教师执教的“锐角三角函数”(北师大版九年级下册第一章第一节第1课时),引发笔者对概念教学的进一步思考,现整理成文,以期与同行交流.
一、教学片断简录及评析
1.教学片断1(由教师A执教)
一上课,直接点出课题,指出为了研究锐角三角函数,先从梯子的倾斜程度谈起.
问题1:图1中的梯子AB和EF哪个更陡?
生(众):EF更陡.
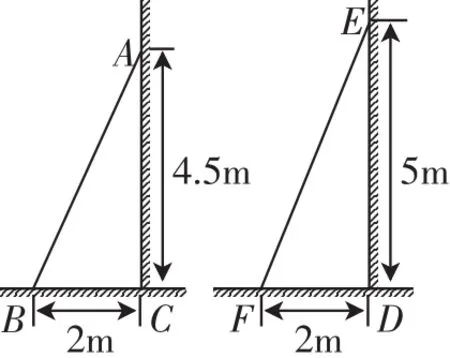
图1
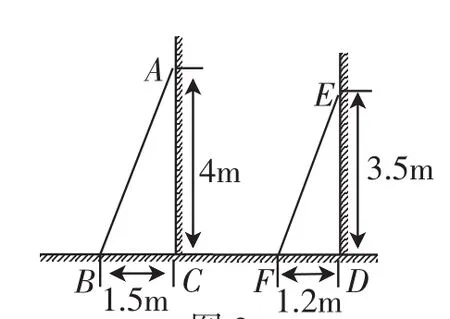
图2
问题2:图2中的梯子AB和EF哪个更陡?你是如何判断的?
学生分组讨论片刻后,教师请一学生介绍思路,该生指出:只要在BC上取点M,使得BM=DF,过M作MN⊥BC交AB于N,由△BMN∽△BCA计算出MN=3.2,根据MN<DE,可判断梯子EF更陡.
教师肯定该生的做法,指出这里运用了化归与转化思想,接着提出以下问题.
学生回答可由△AB1C1∽△ABC得到,教师指出既然的值一样,就把这个值叫做∠A的正切.由此引入正切的概念,至此用时不到10分钟.
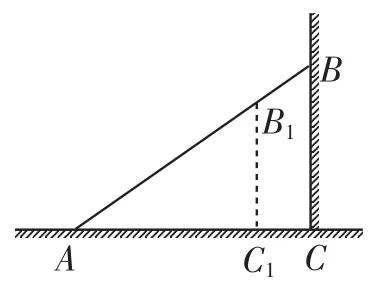
图3
评析:教师意在通过探究梯子的倾斜程度这一情境问题,让学生经历正切概念的形成过程.但在实际教学中,教师基本上按照课本提供的素材,按部就班地完成三个问题的解答,没有利用过渡性语言体现出三个问题之间的关联,也没有很好地发挥情境对正切概念引入的指向作用,而是在问题3后直接给出正切的概念.情境中关注的是“边”对梯子倾斜程度的影响,而正切反映的是直角三角形中边与角之间的关系,这里的关键在于引导学生从对“边”的关注自然过渡到对“边角关系”的探究,显然在这方面本节课做得还很不够,导致所给情境与教学核心内容之间的割裂,情境成了点缀,并没有真正服务于核心内容的教学.
2.教学片断2(由教师B执教)
第二,随着农村经济产权制度改革的深入,农民在集体中的收益分配落到了实处。随着农村现代化进程的不断推进,集体经济所带来的收益呈现出前所未有的高速增长态势,这也使得更多的农民乐于分享集体经济所带来的成果[2]。
上课伊始,引导学生回顾直角三角形的性质:在Rt△ABC中,若∠C=90°,则∠A+∠B=90°,a2+b2=c2,进而提出问题:直角三角形的边与角之间会有什么关系?告知学生要探究直角三角形的边与角之间的关系,可以从梯子的倾斜程度谈起.
师:一个梯子的倾斜程度会与什么量有关?
(学生回答:梯子与地面的夹角,梯子的长,梯子顶端与地面的距离,梯子底端与墙角的距离)
师:梯子的倾斜角(梯子与地面的夹角)与倾斜程度有什么关系?
生(众):倾斜角越大,梯子越陡.
师:如果无法得知倾斜角的大小,而是知道两个梯子的垂直高度和水平宽度,能比较出这两个梯子的倾斜程度吗?来看下面的问题.
问题1:图1中的梯子AB和EF哪个更陡?(两个梯子“同底”,只需比“高”,梯子EF更陡)
问题2:图4中的梯子AB 和EF哪个更陡?(两个梯子“同高”,只需比“底”,梯子EF更陡)
问题3:图2中的梯子AB 和EF哪个更陡?
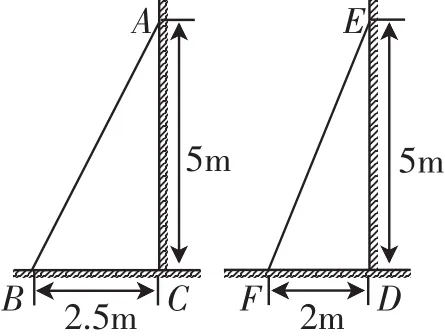
图4
学生分组讨论5分钟后,各组代表到台前交流解题思路,发现梯子EF更陡,并且提出了5种不同的解决办法.教师引导学生归纳各种方法的共同特点:都是通过添加辅助线,把两个直角三角形化为“同底比高”或者“同高比底”.
师:这些方法都比较烦琐,还有更简洁的方法吗?
生:刚才各种方法考虑的都是“高”和“底”,因而只要去计算它们的比就可以.
师:他们的比与梯子的倾斜程度有什么关系呢?
随后教师通过几何画板演示,对学生的猜想进行更多的验证,得出结论:的值越大,梯子越陡(∠A为梯子与水平地面的夹角).
借助图3,教师引导学生由△AB1C1∽△ABC,得到,接着又在AB边上任取一点B2,过点B2作 B2C2⊥AC于C2,学生发现,进而得到结论:在Rt△ABC(∠C=90°)中,当∠A的大小确定后,它的对边与邻边的比值就确定了,与所在直角三角形的大小无关,从而引入正切的概念,至此用时30分钟.
评析:教师首先通过回顾旧知,自然地提出问题“直角三角形的边与角之间会有什么关系?”引发学生的认知冲突,激发他们的探求欲望,让他们兴趣盎然地投入到问题的探究中.接着利用“梯子的倾斜程度”这一问题情境,在教师的引导下,学生自主探究发现:既可以用倾斜角的大小,也可以用的值的大小来判断梯子的倾斜程度,由此顺势提出问题“二者之间会有什么关系”,建立起直角三角形中边与角之间的关联,自然地引入正切概念,让情境直击“课题”,聚焦教学内层,其教学功能得到很好的发挥,整个探究过程似行云流水,一气呵成.在问题3的教学中,教师留给学生充足的探究和交流时间,各组学生积极分享自己的探究成果,发言热情高涨,课堂气氛活跃,在不长的时间里竟然想出了5种不同的解决方案,各种方案精彩纷呈,令人赞叹不已,他们的思维得到淋漓尽致的发挥,主体地位得到很好的落实.
二、教学思考
1.理解教材意图,概念引入自然流畅
读懂教材,领悟编者的意图,是开展有效教学的基础.然而,由于受到条件限制,教材内容往往只能以静态的形式进行呈现,内里蕴含的数学思维要靠教师通过动态的课堂活动才能得以激活.如果教师没有深入理解教材,领会编写意图,课堂上只能是教材内容的“二传手”,各环节的教学将是“碎片化”的,不够连贯,不易建构起完整的知识体系、经历思维过程,培养数学能力更是无从谈起.本节课,教材提供的“探究梯子的倾斜程度”是一个很好的现实情境,取材真实,贴近学生的生活实际.梯子靠墙摆放,既可以通过倾斜角来反映梯子的倾斜程度,也可通过计算其中两边的比来刻画梯子的倾斜程度,引导学生探究“角”与“边”这二者之间的关系能快速指向“锐角三角函数”这一教学核心.根据调查,在已知边的情况下要判断梯子的倾斜程度,学生首先关注的是梯子的“高”与“底”,而不是梯子的长度,这正是教材为什么选择正切作为本章学习起点的原因,如果不做深入思考,就很难体会到隐藏在文字背后的编写意图,挖掘不出暗含其中的教学功能.教学片断1中,教师缺少对教材的加工,导致情境的作用没有得到有效发挥,不能很好地服务于新知的引入,事实上正切的概念是由教师生硬给出的.而在教学片断2中,同样的教学素材,由于教师站在系统的高度上,对教学内容进行重新组织,通过“直角三角形的边与角之间会有什么关系”“它们的比与梯子的倾斜程度有什么关系”“二者之间又有什么关系”等设问,使静态的教材内容动态化,把割裂的问题关联起来,使零星的知识条理化、系统化.教学中,教师以问题为主线,层层递进,直达本课核心,概念的引入自然流畅,符合学生的认知规律,还能让学生体会到数学与生活的密切联系.我们在设计教学时,要对教材进行深入思考,创造性地使用教材,找准数学知识网络的结点,把只有“干货”的教材变得“有血有肉”,活泼灵动,通过设计贴近学生思维最近发展区的数学问题,将教学内容转化为高效的教学行为,让教学内容有序地层层推进,使数学思维之花在和谐的课堂上灿烂绽放.
2.慢化探究过程,概念本质揭示到位
概念的抽象性往往导致学生不易理解,这就需要教师在教学时,慢化概念探究,拉长思维过程,让学生经历概念的形成过程,自主揭示概念的本质,准确把握概念的内涵和外延.当前,数学课堂仍然存在着把速度置顶这种现象,出现了“快餐式”的教学.比如,在概念教学中,有的教师不关心概念产生的背景,不重视概念的形成过程,采用“掐头去尾烧中段”的方式直接告诉学生概念,让学生记住“一个定义,几项注意”,接着举例训练,反复练习.这种急功近利的教学方式缩减了概念探究的历程,影响了学生的深度思考,阻碍了学生思维的发展、能力的提升.片断1的教学中,正切概念的引入用时不到10分钟,概念产生的背景交待得不够到位,概念本质的揭示并不是学生自主完成的,结果就会导致学生对概念的掌握一知半解,应用时是知其然而不知其所以然,只会机械模仿,生搬硬套,致使训练游离于知识之外,长此以往,必然对数学“四基”的落实产生不利影响.当然,我们讲要慢化概念教学,并不是刻意地慢慢吞吞,而是为了把探究的过程、发现的机会留给学生,让他们有足够的时间经历概念的形成,促进知识的有效内化,暂时的慢是为了更好的快.片断2的教学中,概念的引入虽然用时较多,挤压了一些强化练习的时间,似乎很不划算,实则不然,在解决问题3时,学生通过独立思考、小组讨论、分享交流,经历问题解决的全过程,体验了解决方法的多样性,感悟了化归与转化思想,他们在交流碰撞中解决了问题,提升了能力.正因为教师能够慢化探究过程,才会有如此精彩的课堂生成,学生才能收获成功的喜悦,体会数学学习的乐趣,这正是片断1中的教学所达不到的效果.在接下去的活动中,当学生知道既可以用倾斜角的大小,也可以用的值的大小来判断梯子的倾斜程度后,继续探究这二者之间的关系,主动揭示出“在Rt△ABC(∠C=90°)中,当∠A的大小确定时,它的对边与邻边的比值就确定了,与所在直角三角形的大小无关”这一结论,这正是正切概念的本质特征,此时引出正切概念自然是水到渠成.在这种“慢”教学中,学生充分经历概念的形成过程,自主完成概念的建构,理解概念的本质属性,对学到的概念自然是体会深刻,记忆牢固.正如一位学生在课堂小结时所说:“这节课的知识不是老师灌输给我们的,而是自己主动探究获得的,这样获得的知识我将终身难忘.”学生在获取数学知识的同时,思维能力、情感体验等方面都得到了进步和发展,这应是数学课堂不懈的追求!
*本文为江苏省如皋市微型课题《九年级数学教学中激发学生学习兴趣的研究》的研究成果,作者系该课题主持人.
