概率统计教学重在情境引入,贵在挖掘内涵——从一节概率教学公开研讨课谈起
2016-05-03江苏省无锡市塔影中学
☉江苏省无锡市塔影中学 华 琳
概率统计教学重在情境引入,贵在挖掘内涵——从一节概率教学公开研讨课谈起
☉江苏省无锡市塔影中学华琳
一、背景介绍
近日,笔者参加了一次数学教研活动,课题定位概率统计的研讨课“哪种方式更合算”,本课围绕在日常生活中经常会遇到的各种摇奖活动,通过以前的学习,学生已初步认识了在这些活动中获胜或获奖的可能性,但尚未具有正确的评判能力和决策能力展开.从备课到磨课到专家点评,收益颇丰.现将课堂实录展示出来,与各位同行探讨.
二、课堂实录
(一)创设情境,问题引入
也许你曾被大幅的彩票广告所吸引,也许你曾经历过各种摇奖促销活动.你研究过获得各种奖项的可能性吗?你想知道每一次活动的平均收益吗?让我们一起来研究其中的奥秘吧!
师:我们在日常生活中,经常会遇到各种摇奖活动,下面就是一例.
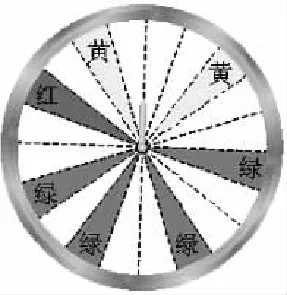
图1
某商场为了吸引顾客,设立了一个可以自由转动的转盘1(如图1),并规定:顾客每购买100元的商品,就能获得一次转动转盘的机会.如果转盘停止后,指针正好对准红色、黄色、绿色区域,那么顾客就可以分别获得100元、50元、20元的购物券,凭购物券可以在该商场继续购物,如果顾客不愿意转转盘,那么可以直接获得购物券10元.转转盘和直接获得购物券,你认为哪种方式更合算?
师:当转盘停止后,指针可能落在哪些区域?获得购物券的机会分别有多大?
生:指针可能指向各种颜色的区域,根据各种颜色的区域在转盘中所占的比例:红色为,黄色为,绿色为,白色为,那么可能获得100元、50元、20元购物券的概率分别为0.05、0.1和0.2,指针指向白色区域的概率为0.65,此时不能获得购物券.
师:如果不转动转盘,可以直接获得购物券10元,如果转动转盘,就会出现多种可能的结果,放弃转动转盘,意味着放弃了获得100元、50元、20元购物券的机会.如果不放弃,就意味着有可能连获得10元购物券的机会也没有了,那么该如何选择比较合算呢?下面我们先来做一个实验,也许你会从中找到解决这个问题的办法.
(二)动手实验,揭示规律
安排学生活动.
(1)每四人组成一个合作学习小组,用课前制作的转盘,通过实验的办法(每组实验100次)分别求出获得100元、50元、20元购物券及未能获得购物券的频率,并据此估计每转动一次转盘所获购物券金额的平均数,看看转转盘和直接获得购物券,哪种方式更合算.
(2)全班交流,看看各小组的结论是否一致,并将各组的数据汇总(如表1),计算每转动一次转盘所获得购物券金额的平均数.
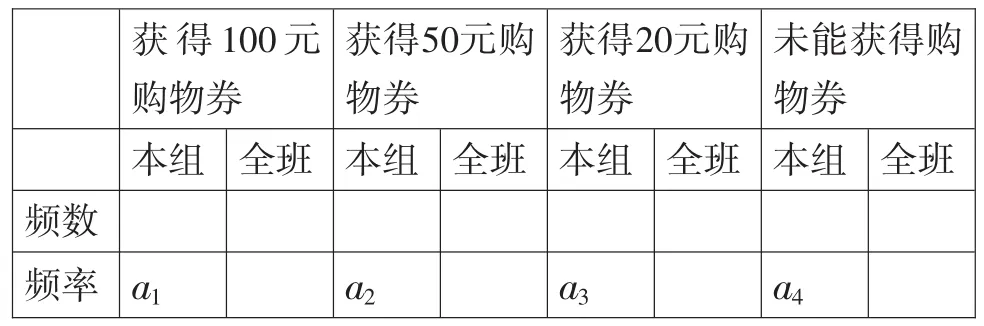
表1:转转盘实验的结果
师:你在实验中是如何计算每转动一次转盘所获购物券金额的平均数的呢?
当做100次实验时,设获得100元购物券的频率为a1,获得50元购物券的频率为a2,获得20元购物券的频率为a3,未能获得购物券的频率为a4,根据加权平均数的定义,可得每转动一次转盘所获购物券金额的平均数为:
100a1+50a2+20a3+0a4=100a1+50a2+20a3(元).
学生从统计表中可以看到汇总全班的数据以后,总体上指针停在每种颜色区域上的频率更接近各颜色的区域与整个转盘的面积比.即当试验次数很大时,a1、a2、a3、a4将稳定于和它相应的理论概率.此时,我们可以用实验频率来估计理论概率.
师:把上图的转盘改为图2所示的转盘2,如果转盘停止后,指针正好对准红色、黄色、绿色区域,那么顾客仍分别获得100元、50元、20元的购物券,与转盘1比,哪一个转盘对顾客更合算?如果改用图3中的转盘3呢?
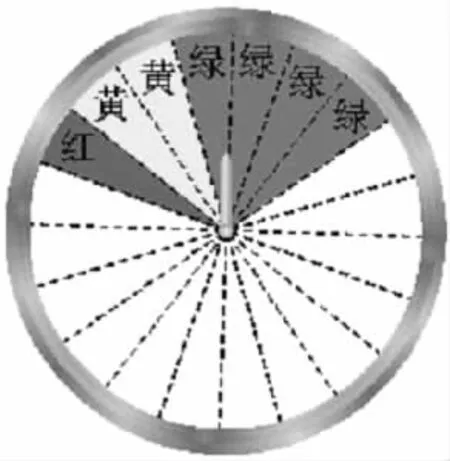
图2
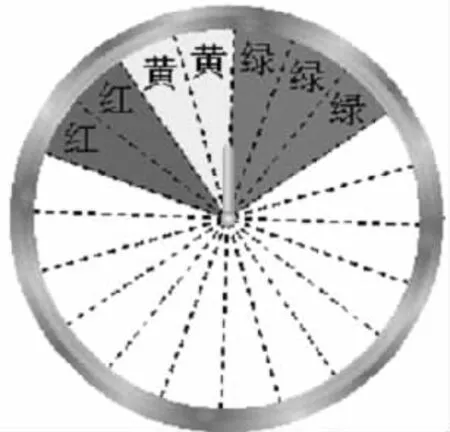
图3
生交流讨论.
师:转盘2和转盘1对顾客而言结果是一样的.因为指针落在红色区域、黄色区域和绿色区域的可能性没有变.转盘3和转盘1对顾客而言结果不一样,转盘3对顾客来说更合算.因为未获购物券和获得50元购物券的可能性没有变化,获得20元购物券的可能性减少,获得100元购物券的可能性增加.
(三)理论计算,构建认知
师:如果不用试验的方法,你能求出每转动一次转盘所获购物券金额的平均数吗?
生:由图2我们知道,每转动一次转盘,获得100元购物券的概率为,获得50元购物券的概率为,获得20元购物券的概率为,理论上可以认为转动n次转盘,获得100元购物券的次数为n次,获得50元购物券的次数为n次,获得20元购物券的次数为n次,所以每转动一次转盘所获购物券金额的平均数应该是:

同理,使用转盘3,每转动一次转盘所获购物券金额的平均数应该是:

师:这种算法我们曾经在哪里用过吗?
生:这种算法与上一节小明估算农村居民的人均纯收入的方法是一致的.
(四)讨论交流,辨析理解
师:小亮根据转盘2,绘制了一个扇形统计图(如图4),据此他认为,每转动一次转盘所获购物券金额的平均数是100×5%+50×10%+20×20%=14(元).你能解释小亮这样做的道理吗?

图4
生:我认为小亮的算法是有道理的.
由图2可知:自由转动转盘,指针落在红色区域、黄色区域、绿色区域的可能性大小即概率分别为、,我们可以把看作权重,因此小亮绘制的扇形统计图,反映了转盘停止转动时,指针指向红色区域、黄色区域、绿色区域的权重.由加权平均数的计算公式就可求出转盘每转动一次所获购物券金额的平均数是:
100×5%+50×10%+20×20%=14(元).
师:按小亮的算法,小明一组转了100次,总共获得购物券应为1400元,可实际上他们总共获得购物券是1320元.这是为什么呢?
生:因为用小亮的方法计算的平均数是用理论概率计算出来的,但实际上的频率很难和理论概率完全相同.
师:大家对实际生活中存在的不确定现象的认识是正确的,其实实验次数很多时,实验结果应该和理论值相近,但实验次数再多,也很难保证实验结果与理论值相等,这是我们作出决策和评判时应该具备的随机观念.
(五)随堂练习,巩固深化
改用另一个转盘进行上面的活动,小颖根据实验数据绘制出扇形统计图(如图5),求每转动一次转盘所获购物券金额的平均数.

图5
生:根据扇形统计图,可知每转动一次转盘所获购物券金额的平均数是:
100×10%+50×15%+20×25%=22.5(元).
(六)归纳总结,自我评价
这节课我们继续经历了解决问题的活动过程,学会如何评判某件事情是否“合算”,通过具体问题情境,掌握了一定的判断方法,提高了决策能力;通过探索“平均收益”的计算方法,领会到随机数学与确定数学之间的联系.经历了实验估计和理论计算的过程,进一步体会到概率与统计之间的联系,更好地建立了随机观念.
三、教学思考
对于概率与统计的教学,在教学中笔者进行了以下的探索与实践,现将几点心得体会与大家交流分享.
1.注重学生的活动,特别是小组合作活动的组织与教学
概率统计的教学难在学生对事件发生的随机性的理解,而要在统计中运用随机性来正确地解决实际问题,对学生又有更高的要求.本课涉及随机变量的均值的计算,对学生的思维具有较大的挑战性,虽然学生已学过加权平均数,但那毕竟是静态的数学.如何将它和频率与概率的知识结合起来,是学生理解理论计算的关键.在交流合作中,通过相互帮助,让所有学生都能得到发展,达到共同进步的目的,获得数学活动经验与体验.
2.教学中数据要真实可靠,呈现方式宜多种多样
教学中,首先,要通过设置适合的问题情境,引起学生的认知冲突,激发学生的探究欲望.其次,要善于寻找知识联系,教师通过构筑认知平台,为学生建立知识联结提供帮助.如引导学生通过列表统计小组数据并汇总全班同学的数据;引导学生理解转盘中的几何概率与实验频率之间的关系;把学过的权重概念和频率联系起来,借助于频率在大数次实验下估计理论概率的核心知识,再过渡到随机变量的均值的理论计算.实现了学生对学过的知识有更进一步的理解又顺应到新知识的建构之中.
3.注意课程资源的利用和开放,培养学生的随机观念
学生对知识的理解需要有个内化的过程,而在学习层面上让学生经历有意义的数学活动十分关键,只有学生在积累了足够的数学经验后,才能自主建构完整的知识体系.因此本课按照“直觉猜想、实验感悟、理论计算、实践应用”的认知规律进行教学设计,充分体现了以学生为主的教学理念.将实验估算和理论计算结合起来,促进学生建立正确的随机观念,并体现随机数学在解决实际问题中的巨大价值.
参考文献:
1.中华人民共和国教育部制定.义务教育数学课程标准(2011年版)[M].北京:北京师范大出版社,2012.
2.展国培.有效教学,从关注学生开始[J].中小学数学(初中),2013(1).
