乒乓球底板结构对底板性能影响研究
2016-05-02季云峰施之皓陈文朴
孙 瑞,李 春,任 杰,朱 玲,季云峰,施之皓,陈文朴
●专题研究 Special Lecture
乒乓球底板结构对底板性能影响研究
孙 瑞1,李 春1,任 杰2,朱 玲2,季云峰2,施之皓2,陈文朴1
底板是乒乓球拍的力量来源,从根本上决定出球的速度和旋转性能。为研究乒乓球底板性能,采用有限元软件,基于模态分析,对不同结构底板数值模拟,分析了木材、碳纤维和玻璃纤维3种不同材料叠合而成的底板前四阶固有频率;计算了同种木材,相同底板总厚度,6种层数下,相邻层纤维方向垂直和平行12种叠合方式的一阶频率;研究了芯材和面材不变,力材纤维角度以15°为步长从0°增加到180°叠合角度对底板性能的影响。得出如下结论:材料对底板固有频率影响很大碳纤维对提高底板弹性效果极佳,一阶固有频率增加40.5%;相同质量时,相比于林巴,碳纤维可提高底板固有频率,玻璃纤维可降低底板固有频率;相邻层纤维方向平行时,底板层数对固有频率无影响;相邻层垂直时,随着底板层数增加,固有频率提高;各层纤维方向均沿拍柄方向时,固有频率达到最大值;各层材料叠合角度也会影响底板性能。叠合角度趋向于90°时,固有频率降低;叠合角度趋向于0°或180°时,固有频率升高。研究结果为设计及分析乒乓球拍底板性能提供了理论依据和实现途径。
乒乓球;底板;模态分析;固有频率;材料
乒乓球是我国“国球”,是一项集速度、力量、落点、旋转和节奏为一体的全民娱乐、健身和竞技体育运动[1-4]。在国际比赛中,中国乒乓球队不断取得佳绩,为祖国赢得了荣耀。自1996年亚特兰大奥运会起,中国连续包揽2000年悉尼奥运会、2008年北京奥运会及2012年伦敦奥运会该项目的4块金牌,今年8月18日的里约奥运会,马龙率领中国男队3∶1战胜日本队获男团冠军再次取得大满贯,进一步巩固了中国在世界乒坛的霸主地位[5]。这些成绩的取得不仅与运动员刻苦训练、顽强拼搏有关,还与体育科研人员对每一项技术的深入研究息息相关。随着计算机模拟技术的成熟和复合材料的发展,使得乒乓球拍底板性能的定量研究成为可能[6-8]。
有关乒乓球的研究,国内外学者已逐渐重视。LIU C等[9]基于球拍反弹模型和空气动力学模型,通过建立非线性方程组,求解两点微分方程的边值问题,预测乒乓球击球点和转速,从而为控制乒乓球机器人手臂挥拍运动提供依据,数值模拟并与实验结果对比证明了方法的可靠性;文献[10]基于动量定理和动量矩定理,构建乒乓球上下旋球碰台后动态特性的数学模型,基于MATLAB编写了仿真程序,通过实例验证了数学模型的准确性和有效性,为增加回球准确性和攻击性提供了理论依据;LIONEL M等[11]基于声振耦合模型,观察实验现象分析了底板材料、厚度和层合板黏合角度对底板性能的影响,测量出不同质量底板声音频率,并与高水平运动员对底板声音的感官分析结果作对比,验证了方法的正确性,但未考虑感官分析的主观性;文献[12]基于有限元软件MSC.MARC,对乒乓球与球拍碰撞过程数值模拟,定性分析了球拍中加入碳纤维含量对球速的改变,初步研究了由传统木材和碳纤维复合材料板叠合而成的乒乓球拍微结构对碰撞后乒乓球运动规律的定性影响,但未能考虑底板叠合角度对其性能影响。
由此可见,目前对于乒乓球运动的分析大多集中于球的运动参数和运动轨迹,涉及乒乓球拍底板的研究不多。而为数不多对于底板的探讨也仅局限于有限的定性分析,亦或运动员的主观感觉。鉴于底板作为乒乓球的力量来源,其性能对碰撞后球的运动参数起决定性作用,重要性无可替代,故定量研究极为必要。
传统乒乓球底板一般由3层或5层等相邻层垂直的木材叠合而成,其组成形式为:面材、力材和芯材,芯材最厚,一般为2.5~5 mm,力材次之,一般为0.5~1 mm,面材最薄,一般为0.2~0.5 mm[13]。底板结构性能与其固有频率密切相关,所谓固有频率是指物体做自由振动时,其位移随时间按正弦或余弦规律变化,振动的频率与初始条件无关,而仅与系统的固有特性有关[14]。底板固有频率越高,硬度越大,出球越速度快,攻击性越强;反之,固有频率越低,硬度越小,球与拍接触时间越长,控球越好[15]。底板性能不仅与所选材料的特性有关,还与设计层数和叠合角度有关[16]。目前,验证底板性能方法主要有2种:运动员感官分析和传感器测量分析。前者依靠主观感觉,准确性差,对于同一块底板,2个运动员员可能会得到完全相反的结论[17];后者依靠实验仪器,费用昂贵,商用的传感器动态性能差、精度低,无法满足实验要求[18]。因此,数值模拟自然成为研究底板特性的重要方法。本文基于有限元软件,实现了乒乓球底板材料叠合,通过数值模拟,对比了不同材料、不同层数和不同叠合角度底板的固有频率,分析了底板性能改变的原因;同时也表明可通过计算机模拟技术解决乒乓球拍性能分析问题,这为更全面地分析和深入研究乒乓球拍底板性能提供了一条更有价值和方便实用的途径。
1 研究方法
有限元法[19]是结构有限元分析的理论基础,即把一个结构看成是由有限个单元通过节点组合而成的整体,利用平衡条件求解它们的位移,然后由节点位移导出各单元内力的一种数值方法。通过将底板模型离散成有限数目的单元体,基于弹性力学基本方程[20]和最小位能原理[21]对每个单元体联立方程求解,得出满足工程精度的近似结果。
通过有限元法将底板模型离散后,单元通过节点传递载荷,则任意单元体的位移向量U可表示为:

式中:U为任意单元体的位移向量;N为形函数矩阵;ue为任意单元体节点的位移向量。
根据连续弹性体的几何方程和式(1),并令B=LN,则任意单元体的应变向量ε可表示为:
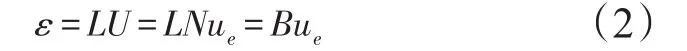
式中:ε为任意单元体的应变向量;L为微分算子;B为单元应变矩阵。
根据连续弹性体的物理方程和式(2),则任意单元体的应力向量σ可表示为:

式中:σ为任意单元体的应力向量;D为弹性矩阵。
根据最小位能原理,在体积域V内,系统总的载荷向量P可表示为:
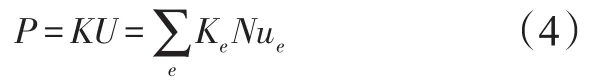
利用结构力和位移边界条件,可求得整个有限元系统的应力、应变、位移及载荷。
另外,根据瞬时最小势能原理,可导出结构的运动微分方程:

式中:M、C分别为系统总的质量矩阵、阻尼矩阵。
当处于自由振动状态,外力为零,故式(5)可表示为:

由式(6)可求得底板的固有频率和振型。
2 数值模拟
2.1 材料属性
常见底板结构中面材为底板最外层,影响软硬程度;力材为底板次外层,直接影响球的反弹;芯材为底板中间层,影响球拍底劲,即球拍受到球的作用力发生弹性形变后恢复到原来形状的快慢,恢复时间短则底劲大,反之,底劲小[22]。本文面材选用克托;力材选用林巴;芯材选用阿尤斯。纤维材料选用玻璃纤维和碳纤维。材料具体属性见表1。
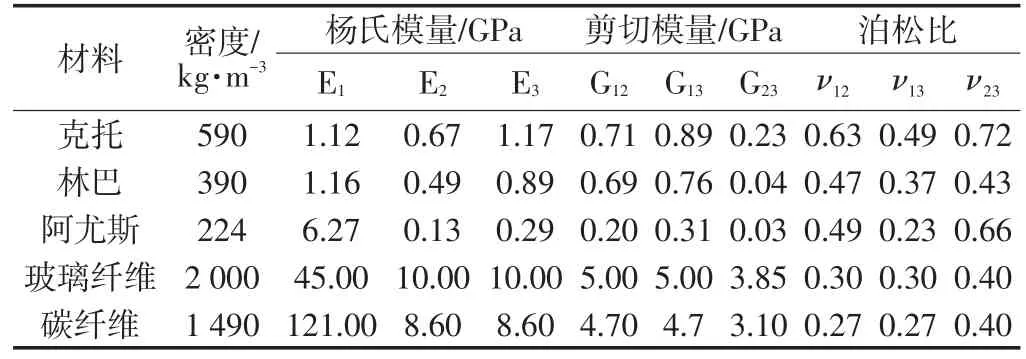
表1 底板材料参数Table1 Properties of materials for table tennis rackets
2.2 实体模型
以某品牌横拍快攻型底板作为研究对象,拍柄选用击球稳定和发力强劲的锥形,底板主体采用5层木板垂直叠合的典型结构。底板最大宽度158 mm,长度150 mm;拍柄最大宽度36 mm,最小宽度27 mm(见图1)。

图1 乒乓球底板实体模型Figure1 Model of table tennis racket
2.3 叠合结构
底板由各项异性的木材或复合纤维构成(见图2)。纤维方向(图中细线所指方向)与拍柄方向(图中x方向)一致,称为纵向,垂直于拍柄方向(图中y方向)称为横向。各层与x正向夹角称为叠合角度。

图2 底板叠合结构Figure2 Composite structure of table tennis racket
3 有效性验证
ANSYS是世界著名的结构动力响应程序,可以用于求解结构和碰撞等问题[23]。本文基于ANSYS workbench的Modal和ACP模块传递数据,计算和分析不同结构下乒乓球底板整体模态。采用边界条件为球拍手柄固定。计算纯木材底板的一阶、二阶、四阶和五阶振型,结果见图3,固有频率见表2。
根据图3,底板蓝色区域表示振幅小,红色区域表示振幅大。拍柄处固定约束,故振幅最小。由于底板结构和约束的对称性,明显看到振型沿拍柄中心处xz平面对称。分析表2,底板各阶固有频率的计算值与文献值相对误差最大仅为0.097 6,对比LIONEL M等[24]的计算结果,各阶模态振型与固有频率基本一致,说明建模、边界条件和有限元划分的正确性,同时证明本文计算结果的有效性。
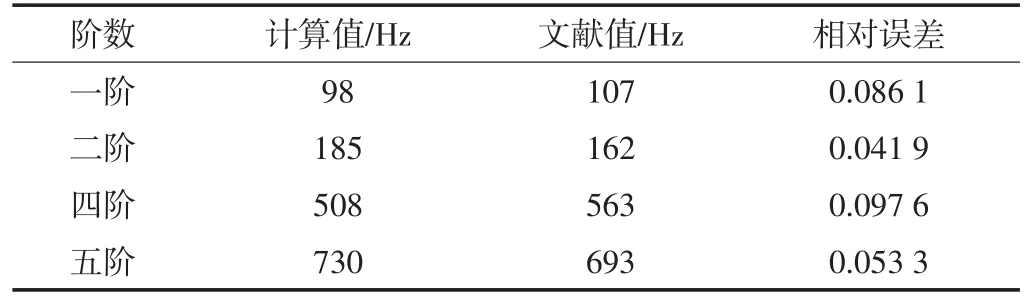
表2 底板固有频率Table2 Natural frequency of racket
4 结果分析
4.1 材料对底板性能的影响
底板芯材厚度3.2 mm,面材厚度0.6 mm,且两者材料不变,改变力材层材料种类,分别采用林巴、玻璃纤维和碳纤维。为保证底板整体质量恒定,三者厚度分别为0.6 mm、0.12 mm和0.15 mm,纤维方向相同,正交于相邻层。研究材料与底板性能的关系,计算前六阶固有频率(见表3)。
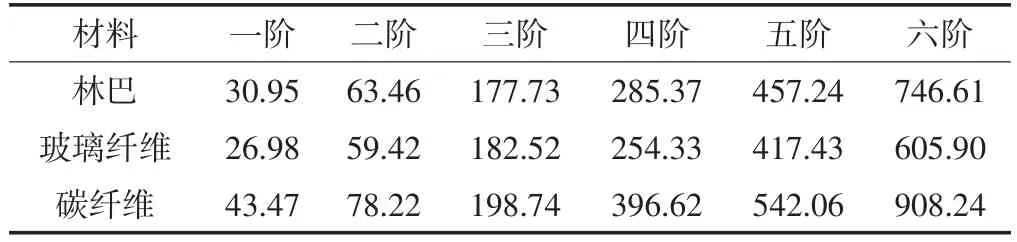
表3 底板前六阶固有频率/HzTable 3 Comparisonofnaturalfrequencyfortabletennisrackets/Hz
表3表明,材料种类影响底板固有频率。与林巴比较,选用玻璃纤维时,各阶固有频率虽有变化,但是幅度不大,最大变化幅度出现在第六阶,仅为18.0%;选用碳纤维替代林巴时,各阶固有频率均有大幅度变化,一阶频率增加最多,达到40.5%。因为玻璃纤维的弹性模量与林巴较为接近,而碳纤维却异于林巴,沿x方向的弹性模量高出103倍。
4.2 层数对底板性能的影响
底板选用同一种木材,总厚度不变,将底板分别等分成1层、3层、5层、7层、9层和11层,计算相邻层材料纤维方向垂直和平行2种叠合方式下底板前四阶固有频率(见图4)。
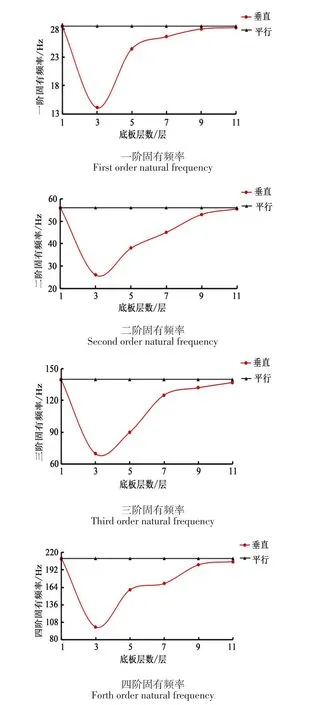
图4 不同层数底板前四阶固有频率Figure4 First 4 Natural frequency of rackets with different layer number
由图4可知,相邻层平行时,前四阶固有频率不随底板层数的增加而变化;相邻层垂直时,单层的底板频率最高,底板分3层的情况下最低。当底板层数大于3时,随着层数增加,固有频率逐渐增加。考虑底板被均分后,从层数为3开始,横向纤维比重逐渐降低,底板频率升高。当所有纤维均沿纵向时,固有频率达到最大值,即底板只有1层时,频率最高。
4.3 角度对底板性能的影响
底板芯材和面材的厚度与材料种类不变,力材分别采用林巴、碳纤维和玻璃纤维,叠合角度由0°增加到180°,步长为15°,共39种不同底板结构。前固有频率计算结果见图5。
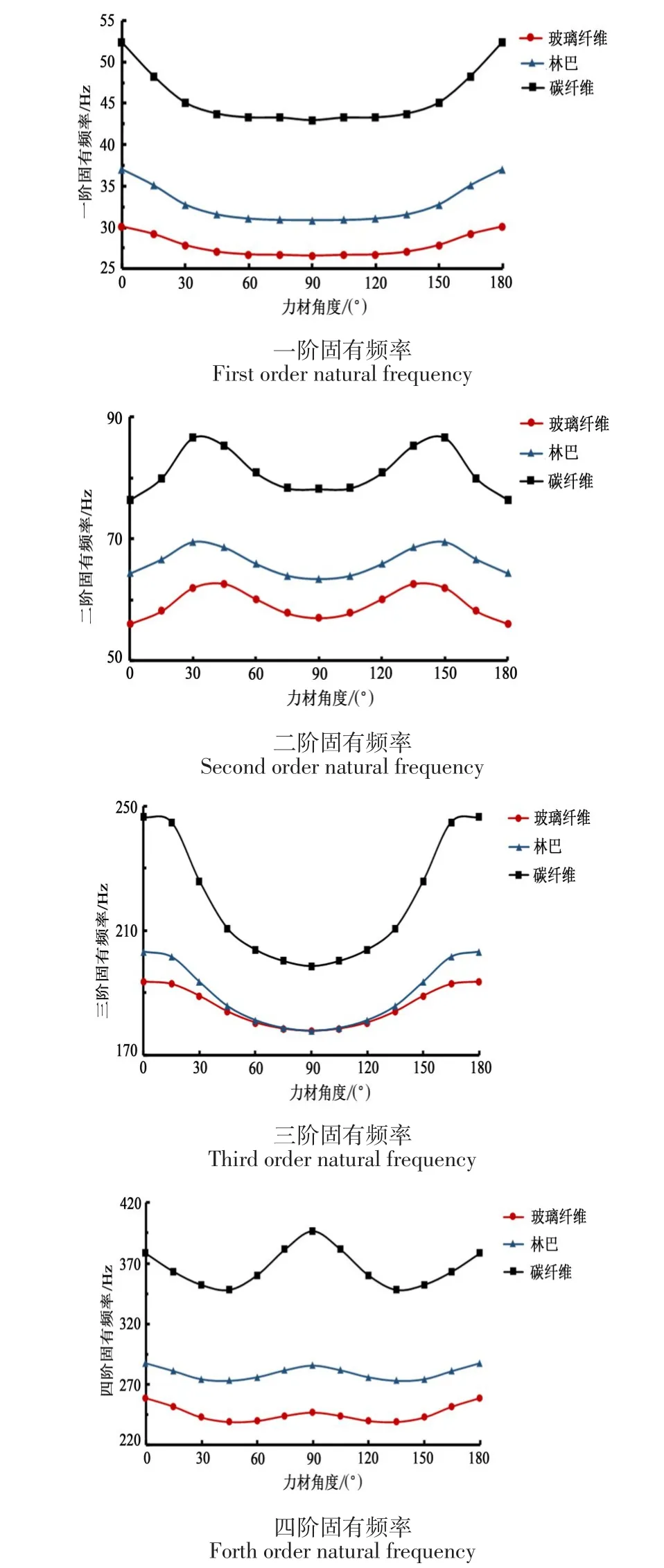
图5 不同材料和不同角度底板前四阶固有频率Figure5 First 4 natural frequency of rackets with different materials and different angles
由图5可知,相同角度时,碳纤维的各阶固有频率均最大,林巴次之,玻璃纤维最小,此结论与表3相符,验证了计算结果和表3结论的正确性。如图所示,3种材料的前四阶固有频率以90°对称,考虑xy平面内叠合角度具有对称性,进一步证明图4计算结果的有效性。随着叠合角度趋向90°,底板力材选用林巴、碳纤维和玻璃纤维的一阶和三阶固有频率均下降,在90°出现峰值。其原因为,随着横向纤维比例降低,底板固有频率逐渐变大,同时该结论与图4所得结论一致,验证了计算结果的可靠性。
5 结论
本文基于ANSYS Workbench平台并结合模态分析理论,将数值模拟应用到乒乓球底板性能研究中。分析了木材、碳纤维和玻璃纤维3种不同材料叠合而成的底板前四阶固有频率;计算了同种木材,相同底板总厚度,6种层数下,相邻层纤维方向垂直和平行12种叠合方式的一阶频率;研究了芯材和面材不变,力材纤维角度以15°为步长从0°增加到180°叠合角度对底板性能的影响。得出如下结论:
(1)材料对底板固有频率影响很大。相同质量时,相比于林巴,碳纤维可提高底板固有频率,玻璃纤维可降低底板固有频率
(2)相邻层纤维方向平行时,底板层数对固有频率无影响;相邻层垂直时,随着底板层数增加,固有频率提高;各层纤维方向均沿拍柄方向时,固有频率达到最大值。
(3)各层材料叠合角度也会影响底板性能。叠合角度趋向于90°时,固有频率降低;叠合角度趋向于0°或180°时,固有频率升高。
本文研究表明可以通过计算机模拟研究乒乓球底板性能,为更全面地设计分析有关乒乓球板问题提供了理论基础和实现技术,同时为不同打法运动员选择底板类型提供了参考依据。
[1]KAWAZOE Y,SUZUKI D.Prediction of Table Tennis Racket Restitu⁃tion Performance Based on the Impact Analysis[J].Theoretical&Ap⁃plied Mechanics Japan,2003,52(2):163-174.
[2]KONISHI Y,OKUIZUMI H,OHNO T.PIV Measurement of a Flying Table Tennis Ball[J].Procedia Engineering,2016,147(6):104-109.
[3]王阜存.乒乓球教学训练法[M].北京:人民体育出版社,2008:35.
[4]宛祝平,杨志亭.乒乓球[M].长春:吉林科学技术出版社,2008:16.
[5]窦远行.中国乒乓球队历届奥运战绩:里约第5次包揽金牌[EB/OL].(2016-08-16)[2016-10-10].http://news.sohu.com/20160818/n464841 590.shtml.
[6]房杰.运用计算机仿真技术对乒乓球碰撞的研究[J].天津体育学院学报,2003,18(3):47-49.
[7]MARTIN P A.Wood Composites[M].Cambridge:Woodhead Publish⁃ing,2015:69-89.
[8]IMAN F,ROHOLLA V,MARJAN R,et al.Contextual Interference in Learning Three Table Tennis Services[J].Procedia-Social and Behav⁃ioral Sciences,2015,191(6):546-549.
[9]LIU C,HAYAKAWA Y,NAKASHIMA A.Racket control and its ex⁃periments for robot playing table tennis[C]//Guangzhou:IEEE Interna⁃tional Conference on Robotics and Biomimetics.IEEE,2012:266-280.
[10]杨春卉,袁志华,梁振刚.乒乓球反弹动态特性的仿真研究[J].计算机仿真,2014,31(10):281-285.
[11]MANIN L,POGGI M,BERTRAND C,et al.Vibro-acoustic of Table Tennis Rackets.Influence of the Plywood Design Parameters.Experi⁃mental and Sensory Analyses[J].Procedia Engineering,2014,72(5):374-379.
[12]武秀根,郑百林,贺鹏飞.乒乓球拍微结构对乒乓球与球拍碰撞过程的研究[J].体育科研,2006,27(2):59-61.
[13]王吉生.乒乓球拍探秘[M].北京:人民体育出版社,2007:78.
[14]RAO S S.Mechanical vibrations[M].New Jersey:Addison-Wesley,1963:26.
[15]潘施伊.乒乓球教程[M].北京:北京理工大学出版社,2011:65.
[16]丁树德.乒乓球[M].上海:上海人民出版社,1976:12.
[17]MANIN L,GABERT F,POGGI M,et al.Vibro-acoustic of table ten⁃nis rackets at ball impact:influence of the blade plywood composition [J].Procedia Engineering,2012,34(4):604-609.
[18]范红波,何忠波.装备磨粒在线监测传感技术[M].北京:国防工业出版社,2013:9.
[19]陈文朴,李春,阳君,等.对比分析不同材料及铺层对叶片力学性能的影响[J].能源工程,2015,15(5):15-19.
[20]宋学官,蔡林,张华.ANSYS流固耦合分析与工程实例[M].北京:中国水利水电出版社,2012:78.
[21]戴春晖,刘钧,曾竟成,等.复合材料风电叶片的发展现状及若干问题的对策[J].玻璃钢/复合材料,2008,1(3):53-56.
[22]杨桦.乒乓球运动教程[M].北京:北京体育大学出版社,2014:46.
[23]NAKASONE Y,YOSHIMOTO S,STOLARSKI T A.Engineering Analysis with ANSYS Software[M].Oxford:Butterworth-Heinemann,2006:18.
[24]MANIN L,POGGI M,HAVARD N.Vibrations of table tennis racket composite wood blades:modeling and experiments[J].Procedia Engi⁃neering,2012,34(2):694-699.
The Effect of Table Tennis Racket Paddle Fiber Layer on Racket Performance
SUN Rui1,LI Chun1,REN Jie2,ZHU Ling2,SHI Zhihao2,CHEN Wenpu1
(1.School of Energy and Power Engineering,University of Shanghai for Science and Technology,Shanghai 200093,China;2.China Table Tennis College,Shanghai University of Sport,Shanghai 200438,China)
The paddle is the source of table tennis,fundamentally determining the speed and spinning performance of the ball.In order to analyze the perfor⁃mance of table tennis,we simulated numerically different structural floor based on modal analysis by finite element software.We analyzed the first four natural frequencies of paddle made by wood,carbon fiber and glass fiber;calculated the first-order frequency of 12 kinds of superposition which had the same materi⁃al and thickness with six layers while fiber directions of the adjacent layers are vertical and parallel;consider the effect to properties of paddle while the angle of bottom plate increase from 0°to 180°at 15°and the core material and face material are constant.Conclusions are as follows:Material effects the natural fre⁃quency greatly,Carbon fiber can improve the performance of paddle,increasing the first order of natural frequency over 40.5%.When the mass is same,the adding of layer leads the increasing of the paddle.And using the same material,the natural frequency has a biggest value when all the fibers are along the lon⁃gitudinal distribution.As the angle of force wood tends to 90°,the paddle has a higher natural frequency,a lower hardness and control the ball better which is suitable for defensive player;while the angle of force wood tends to 0°or 180°,the paddle has a lower natural frequency,a higher hardness and provide the ball a larger speed which is suitable for defensive player.The results provide a theoretical reference for designing and analysis different types of the table ten⁃nis racket.
table tennis;paddle;modal analysis;natural frequency;material
G 846
A
1005-0000(2016)06-519-05
10.13297/j.cnki.issn1005-0000.2016.06.011
2016-09-14;
2016-11-10;录用日期:2016-11-11
国家自然基金项目(项目编号:51676131);上海市“晨光计划”项目资助(项目编号:13CG55)
孙瑞(1993-),男,安徽合肥人,在读硕士研究生,研究方向为结构数值模拟;通信作者:李 春(1963-),男,北京市人,教授,博士生导师,博士,研究方向为流体机械及工程、叶轮机械气动力学及风能利用。
1.上海理工大学能源与动力工程学院,上海200093;2.上海体育学院中国乒乓球学院,上海200438。
