我对函数定义域的理解与掌握



我对函数定义域的理解与掌握

■田思繁

数学由于其高度的概括性、深奥的抽象性和严密的逻辑性使很多同学学习起来不得要领，有的同学甚至说数学是最感头疼的学科。其实整个数学宫殿的基石就是数学概念，任何数学公式、定理、推论、法则都蕴含在数学概念中，那种只重视解题方法而忽视基本概念的做法是错误的、片面的。因此，要真正学好数学就必须准确把握概念的内涵和外延，只有这样才能不断提高分析问题和解决问题的能力，为全面掌握数学知识奠定良好的基础。函数是高中数学的一条主线，而定义域是函数的灵魂，因此，我在学习函数的过程中始终以优先考虑函数定义域为原则，收到了事半功倍的学习效果。

一、函数值域与定义域

函数的值域是该函数全体函数值的集合，当定义域和对应法则确定后，函数值也随之而定，因此在求函数值域时，应注意函数的定义域。

例1实数x、y满足3x2+2y2=6x,求u=x2+y2的取值范围。

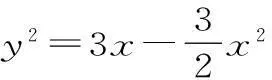
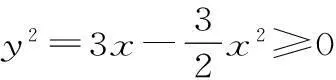
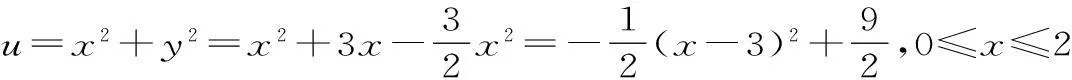
二、函数单调性与定义域

函数单调性是指函数在给定的定义域区间上函数自变量增加时，函数值随着增减的情况，单调性是对区间而言的，是函数的一个局部性质。所以讨论函数单调性必须在给定的定义域区间上进行。

例2求函数f(x)=log0.5(x2+4x+3)的单调区间。

错解：因0<0.5<1，则f(x)为减函数。令g(x)=x2+4x+3，则g(x)=(x+2)2-1。所以，当x<-2时,g(x)为减函数，而f(x)为增函数；当x>-2时，g(x)为增函数，而f(x)为减函数。故函数f(x)的单调增区间为(-∞，-2)，单调减区间为(-2，+∞)。

分析：函数f(x)=log0.5(x2+4x+3)的定义域为(-∞，-3)∪(-1，+∞)，而函数g(x)=x2+4x+3的定义域为R，显然x=-2不属于(-∞,-3)∪(-1,+∞)，可以看出上述错解无形中扩大了函数的定义域。

正解：函数f(x)的单调增与减区间分别为(-∞，-3)与(-1，+∞)。

三、函数奇偶性与定义域

函数的奇偶性是函数的“全局性质”，研究函数的奇偶性要在整个定义域内研究，而定义域关于原点对称是函数具有奇偶性的一个必要条件，故判断前应先考虑该函数定义域是否关于原点对称，如果定义域不关于原点对称，则函数就是非奇非偶函数。

例3判断函数y=x3,x∈[-1,2]的奇偶性。

错解：因为f(-x)=(-x)3=-x3=-f(x)，所以函数y=x3，x∈[-1,2]，是奇函数。

分析：判断函数的定义域是否关于原点对称，是同学们极易忽视的步骤，也是造成结论错误的原因。

正解：因2∈[-1,2]，而-2∉[-1,2]，则函数的定义域区间[-1,2]关于原点不对称，则函数y=x3，x∈[-1,2]，是非奇非偶函数。

四、函数的周期性与定义域

讨论函数的周期性同讨论函数的其他性质一样，不能忽视函数的定义域。

例4函数y=sinx(x≠0且x∈R)是周期函数吗？

分析：此题易给出是周期函数的错误答案，导致错误的原因是忽视了函数的定义域。这是因为假设函数是周期函数，并设其周期为T(T≠0)，那么根据周期函数的定义知，对一切x∈R，x≠0都有sin(x+T)=sinx成立。但实际上此式当x=-T时不成立，此时sin(x+T)无定义，故y=sinx(x≠0且x∈R)不是周期函数。

综上所述，在求解函数问题时，优先考虑函数的定义域是解题的致胜法宝，同时还能培养自己的思维严谨性，提高自己的解题能力。以上是我的一点学习总结，供同学们参考。

作者单位：郑州一中1607班