典型排列组合问题的解决方法例析



典型排列组合问题的解决方法例析

■陈坤

排列组合问题往往涉及多个解决问题的方法，下面以两个典型的例题就具体的方法进行总结和归类。

一、典型的排列问题

例13个女生和5个男生排成一排。

(1)如果女生全排在一起，有多少种不同的排法？

(2)如果女生都不相邻，有多少种不同的排法？

(3)如果女生不站在两端，有多少种不同的排法？

(4)其中甲必须排在乙前面(可不相邻)，有多少种不同的排法？

(5)其中甲不站在左端，乙不站在右端，有多少种不同的排法？

(5)甲、乙为特殊元素，左、右两边为特殊位置。

点评：(1)对于有限制条件的排列问题，分析问题时有位置分析法、元素分析法，在实际进行排列时一般采用特殊元素优先原则，即先安排有限制条件的元素或有限制条件的位置，对于分类过多的问题可以采用间接法。

(2)对相邻问题采用捆绑法、不相邻问题采用插空法、定序问题采用倍缩法是解决有限制条件的排列问题的常用方法。

二、典型的组合问题

例2男运动员6名，女运动员4名，其中男女队长各1人。选派5人外出比赛。在下列情形中各有多少种选派方法？

(1)男运动员3名，女运动员2名；

(2)至少有1名女运动员；

(3)队长中至少有1人参加；

(4)既要有队长，又要有女运动员。

(2)法一：至少有1名女运动员包括以下几种情况：

1女4男，2女3男，3女2男，4女1男。

法二：“至少有1名女运动员”的反面为“全是男运动员”，可用间接法求解。

(3)法一：(直接法)可分类求解。

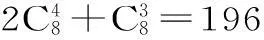
点评：组合问题常有以下两类题型：(1)“含有”或“不含有”某些元素的组合题型：“含”，则先将这些元素取出，再由另外元素补足；“不含”，则先将这些元素剔除，再从剩下的元素中去选取。

(2)“至少”或“最多”含有几个元素的题型：若直接法分类复杂时，逆向思维，间接求解。

作者单位：江苏省滨海中学