航天器柔性附件对整器固有振动特性影响因素及规律分析
2016-04-27郭其威唐国安
郭其威, 吴 松, 刘 芳, 唐国安
(1.上海市空间结构机构重点实验室,上海 201108; 2.上海宇航系统工程研究所,上海 201109;3.复旦大学 力学与工程科学系,上海 200433)
航天器柔性附件对整器固有振动特性影响因素及规律分析
郭其威1,2, 吴松1,2, 刘芳1,2, 唐国安3
(1.上海市空间结构机构重点实验室,上海201108; 2.上海宇航系统工程研究所,上海201109;3.复旦大学 力学与工程科学系,上海200433)
摘要:介绍快速求解含大型柔性附件航天器系统模态的结构动力学方法,通过对多个柔性结构模型缩聚大幅度缩减自由度,集成MATLAB与NASTRAN进行联合仿真分析。遍历附件所有可能工作姿态的系统模态,大幅提高系统模态计算效率。通过该快速求解方法进行仿真实例分析,阐明航天飞行器的系统构型、柔性附件转动角度、本体与柔性附件质量惯量比三方面对柔性附件约束模态与系统模态影响规律。
关键词:航天器;柔性附件;振动;频率
航天器柔性附件在界面固定条件固有振动频率设计中称为约束模态。柔性附件与航天器本体组合后的固有振动模态称为系统模态。柔性附件约束模态与航天器系统模态耦合关系受航天器本体质量、惯量特性、对称或不对称构型布局及连接条件等因素影响。
约束模态对应的频率特性是航天器大型柔性附件(如大面积太阳电池翼、大型展开天线等)设计过程中需关注的重要约束指标,该指标由航天器控制系统带宽需求确定。柔性附件频率特性测试一般通过地面固支状态模态试验及飞行试验状态通过速率陀螺信息辨识获得。以基频为例,据以往飞行试验数据,在轨实测数据通常大于柔性附件自身固支约束模态频率(地面空气阻力影响已通过数值方法去除[1-2])。飞行试验与地面试验相比,柔性附件边界发生变化,飞行试验下航天器组合体呈自由状态,航天器自身质量惯量特性较地面试验状态的“固支”产生弱化。飞行试验状态下柔性附件频率升高现象,可定性的通过模态展开定理[3]解释。
关于柔性附件约束模态与飞行状态下系统模态之间的关系已有诸多研究。章仁为[4]认为挠性卫星姿态运动的系统频率为非约束模态频率,并给出共位控制模型中柔性附件系统模态与约束模态之关系,即
(1)
式中:Λi为柔性附件飞行状态系统频率;λi为柔性附件固支状态下约束模态频率;ki为各阶模态增益。
徐小胜等[5]基于航天器部件模态与系统模态间的恒等式导出柔性航天器在轨自由飞行状态下系统模态频率的估算公式。以上两方法中均需以柔性附件的动力学信息(频率、振型)作为已知量输入完成其余推导,各有优缺点。文献[2]中柔性附件各阶模态增益需已知其振型并进行耦合系数矩阵计算,但在系统模态计算中无法反映柔性附件反对称等振型信息;而文献[3]中仅给出系统模态基频的估算公式,其余高阶模态信息暂未给出。
虽通用有限元程序已具备分析大型航天器系统模态能力,但由于航天器构型复杂,不仅含多个舱段并携带柔性附件,且每个附件与主体坐标系角度关系均会因任务需要进行调整。图1即我国在研空间站工程构型3个舱段、3个副柔性太阳电池翼,系统模态分析时需考虑附件角度组合状态异常复杂,若直接利用通用有限元程序不进行二次开发,计算效率难以满足工程设计需求。

图1 在研空间站工程构型示意图Fig.1 Diagram of space station in research
本文利用集成通用有限元分析程序NASTRAN及科学计算程序MATLAB对附件进行模型缩聚及姿态快速遍历,实现快速求解含大型柔性附件的复杂航天器系统模态。在此基础上研究影响航天器系统模态的各种主要因素及柔性附件约束模态与系统模态间的变化规律。
1复杂构型航天器系统模态分析流程设计
为实现多附件、多姿态的复杂构型航天器系统模态快速分析,所用计算流程见图2。其中曲边底线方块表示定义模型数据的文本文件,矩形方块表示程序模块。流程主体是姿态遍历循环,据设计要求设定各附件所有可能的工作姿态,并在每种姿态下分析系统模态。
系统中诸多柔性附件需用详细有限元模型描述,如索网编织与杆系连接的半刚性、柔性太阳电池翼及大型薄膜天线等。此类结构模型自由度数庞大,需通过模型缩聚(含修正)大幅度缩减自由度。

图2 系统模态分析流程Fig.2 Analysis process of system mode
经附件模型预处理后复杂构型航天器系统模型由本体模型、附件缩聚模型及定义姿态附件坐标系构成。本体及附件简化或缩聚模型分别按有限元程序NASTRAN格式定义为独立文本文件[6],而定义附件坐标系的文本文件则在循环过程中据附件姿态角度、由科学计算程序MATLAB自动生成。编写MATLAB程序脚本、控制姿态遍历循环并以运行外部程序方式运行NASTRAN分析系统模态,从而高效、自动实现多附件、多姿态复杂构型航天器系统模态分析。
2复杂构型航天器系统模态分析预处理
2.1坐标系设置

图3 柔性附件航天器示意图Fig.3 Diagram of spacecraft with flexible annex
复杂构型航天器的柔性附件存在机构运动,为便于将任意姿态角度下柔性附件(缩聚)模型组装到整体系统,引入3个坐标系见图3。其中,x″y″z″用于定义柔性附件模型中单元属性,如索网编织及复合材料铺层方向、杆系构件截面惯量方向等,属于底层坐标系。x′y′z′描述柔性附件状态位置附件,据附件与本体相对角度确定,用于组装系统模型,坐标参数由MATLAB计算。xyz用于描述本体顶层,考虑系统整体设计需要,本体坐标系原点并非本体质心。
2.2航天器本体定义
航天器附带的柔性附件频率通常在0.1~0.3 Hz范围内,而航天器本体自由状态频率则远高于该频率。因此,设计初期可只考虑质量、惯量特性,不计弹性且视为六自由度刚体。
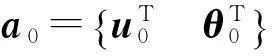
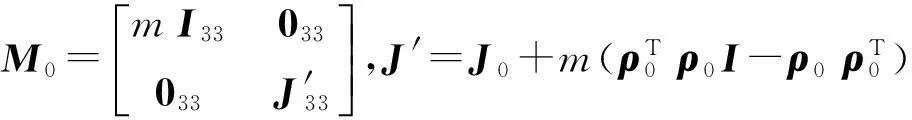
式中:m为本体质量;J0为本体关于质心的主惯性矩矩阵;ρ0为本体质心关于xyz原点的坐标矢量。
2.3柔性附件定义及缩聚
柔性附件模型含复合材料、蜂窝结构等方向敏感单元,须引入单元局部坐标系x″y″z″定义属性。各单元类型在该坐标系下形成的单元刚度及质量矩阵记为k″e及m″e。分别用a″e,a′e表示坐标系x″y″z″及x′y′z′下单元节点位移向量,则坐标转换关系为
a″e=T″ea′e
(3)
式中:T″e为变换矩阵,可据两坐标系间坐标轴方向余弦确定。
单元在附件坐标系x′y′z′下刚度、质量矩阵为
(4)
将柔性附件所有单元按自由度排序并组集获得附件的整体刚度及质量矩阵K′c及M′c,下标c为附件序号。柔性附件结构动力学设计通常包括地面模态试验前仿真预示、地面试验、试验后动力学模型修正3阶段。基于地面超低频模态试验的动力学模型修正过程在此不讨论,以修正后柔性附件动力学模型为原始输入,模型缩聚以附件刚度矩阵K′c及质量矩阵M′c为基础。对部件c,将坐标系x′y′z′节点位移向量划分成内部位移向量a′ci及连接点位移向量a′cj,附件质量、刚度矩阵写成块矩阵,即
(5)
为书写简便略去块矩阵中附件下标c,附件模型用固定界面模态综合法进行动力学缩聚,即
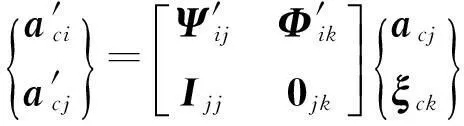
(6)
式中:Ψ′ij为约束模态;Φ′ik为附件固定界面主模态;ξck为附件弹性振动模态坐标。
缩聚后附件质量、刚度矩阵分别为
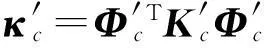
(7)
缩聚模型界面位移从坐标系x′y′z′到xyz的变换关系为acj=T′jja′cj。由于模态坐标ξck只影响附件内部位移,不影响界面位移。因此,从附件坐标系到本体坐标系变换时只需考虑a′cj变换,变换矩阵为

(8)
缩聚后附件在坐标系xyz下的质量、刚度矩阵为
(9)
3本体与附件的耦合

uc=u0+θ0ρc=u0+R0θ0, θc=θ0
(10)
式中:
(11)
因此,附件c连接点位移向量及模态坐标为
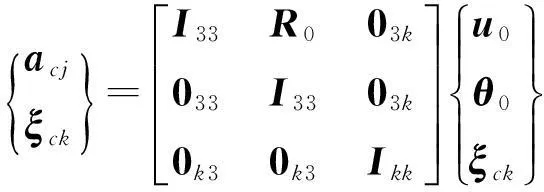
(12)
参与系统组装的附件质量及刚度矩阵为
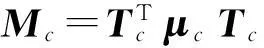
(13)
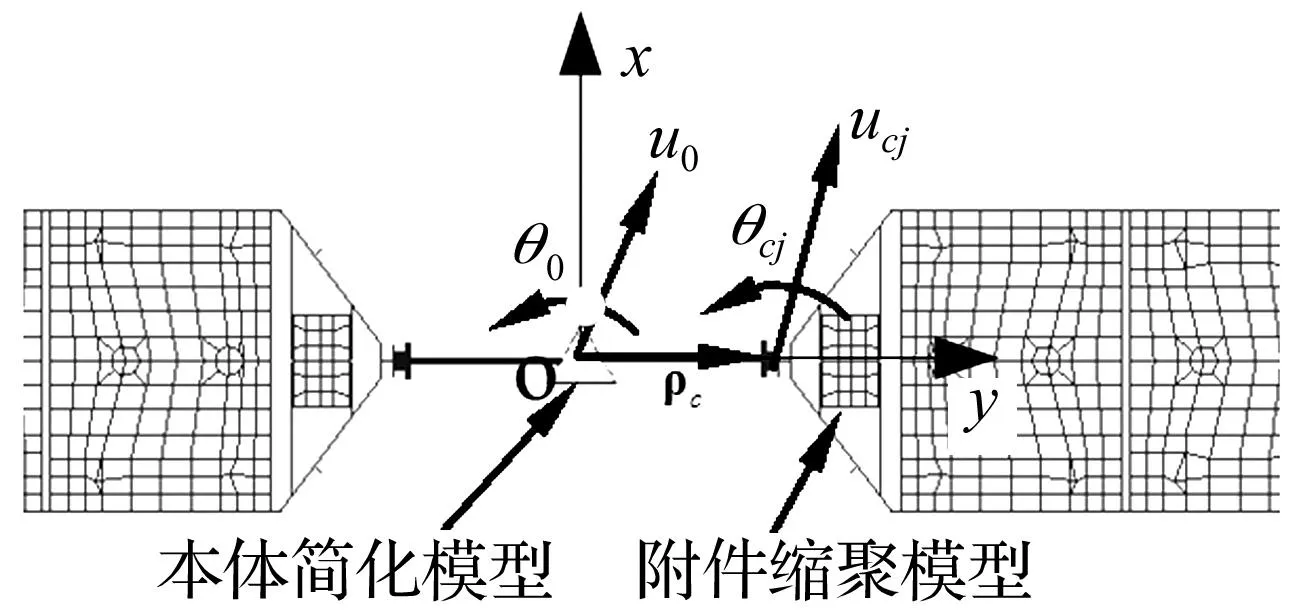
图4 动力学简化处理建模Fig.4 Simplifieddynamical model
将本体矩阵M0,K0及各附件矩阵Mc,Kc据有限元装配过程进行组装即可获得复杂构型航天器系统矩阵M,K,求出广义特征值后便可获得系统固有频率及模态向量。
4系统模态影响因素分析
由柔性附件与本体组合的航天器系统频率受构型、柔性附件姿态角度、本体与附件质量/惯量比等多因素影响,航天器型号会因任务不同安装的柔性附件数量及布局也不同,设计时需全面考虑。以太阳电池翼为柔性附件实例,考虑单、双侧电池翼布局的不同整器构型,遍历电池翼对日定向过程的姿态角度,分析整器系统频率及规律。
4.1柔性电池翼模型缩聚
对柔性附件进行模型缩聚可提高计算效率。某姿态下缩聚前后系统模态计算结果见表1。

表1 同一姿态下缩聚前后系统频率
4.2构型对系统特性影响
按图4坐标系,本体视为中心刚体,质量m=8 000 kg,惯量J0x=8 506 kgm2,J0y=J0z=52 674 kgm2。太阳电池翼质量m=59.9 kg,惯量Jx′=1 490 kgm2,Jy′=19.1 kgm2,Jz′=1 510 kgm2,根部约束条件下一阶弯曲及侧摆频率分别为0.181 Hz与1.25 Hz。本体质量远大于附件质量,而两者惯量比较接近,此为航天器典型的本体与附件质量/惯量分配关系。
单、双侧电池翼布局的航天器系统频率计算结果见表2。由表2看出,①单侧加装电池翼构型的航天器由于电池翼边界条件非理想的固支状态,且本体与电池翼的惯量比较小不能抑制本体转动,因此系统频率较单电池翼频率有所升高,一阶弯曲模态频率从0.181 Hz升至0.193 Hz,一阶侧摆模态频率从1.25 Hz升至1.274 Hz;②双侧加装电池翼构型的航天器有两侧电池翼同向、反向振动两种系统模态。同向振动时系统频率与单电池翼频率较接近,因同向振动两侧电池翼能约束本体转动,而本体与附件质量比较大,使电池翼根部接近理想约束状态;反向振动时系统频率则高于单电池翼频率,原因与单侧布局构型航天器类似。
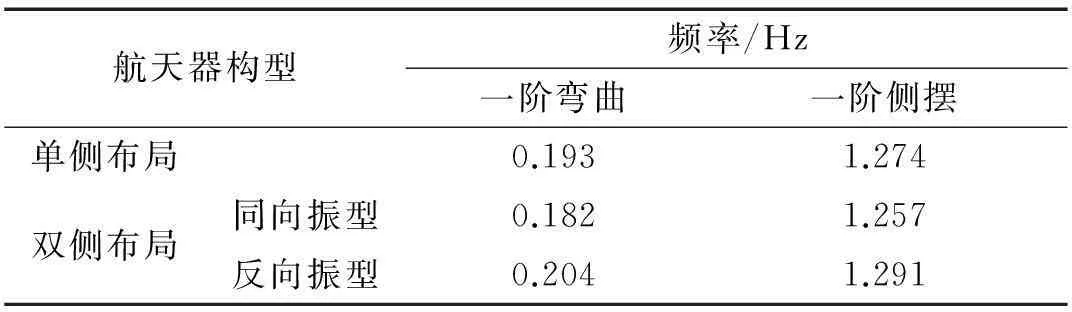
表2 单/双侧太阳电池翼构型对系统频率影响
4.3电池翼姿态角度对系统频率影响
为提高光-电转换效率,太阳电池翼需实时对日定向,在机构驱动下慢速转动,且随角度变化改变电池翼相对总体坐标系各方向惯量,导致系统频率发生变化。控制系统设计需确定系统模态最小频率值为依据,进行系统模态频率分析时须考虑附件姿态角度影响。
两种航天器本体惯量参数见表3。采用航天器系统频率集成分析方法,遍历太阳电池翼各姿态角度,计算对应两种航天器本体惯量参数下电池翼转动角度对系统频率影响,见图5。由图5看出,①电池翼周期性转动,会导致系统频率产生周期性波动;②本体与电池翼质量及惯量比较大时系统频率波动幅度较小。反之,系统频率波动振幅较大,即本体质量或惯量越大对电池翼约束能力越强;③系统频率均不同程度高于柔性附件自身约束模态频率。
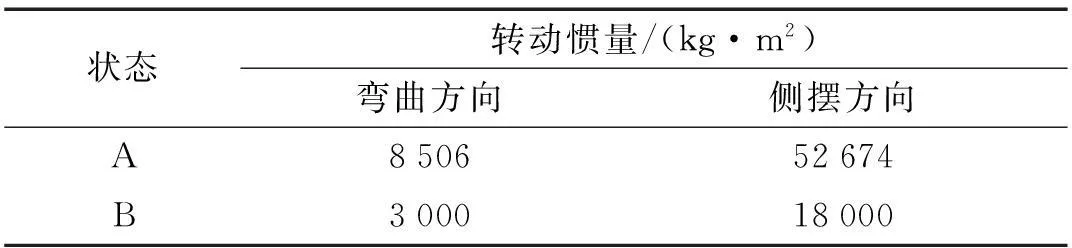
表3 两种单侧电池翼布局航天器本体惯量
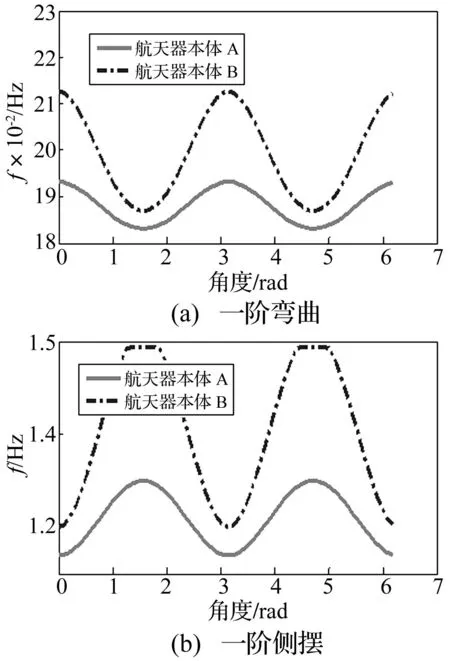
图5 系统频率随转动角度变化Fig.5 Thechange ofsystem frequencywithrotation angle
4.4本体-电池翼质量/惯量比对系统频率影响
航天器本体与柔性附件的质量、惯量比直接反映出二者间动力学耦合程度,与控制系统模态增益定义一致。二者质量、惯量比值可决定柔性附件约束模态与系统模态间变化幅度(即柔性附件地面测试频率值与系统频率在轨辨识频率值间差异)。
在本体与电池翼不同惯量比下航天器整器弯曲、侧摆方向频率变化(实线)见图6。为便于比对,将电池翼约束模态频率用虚线表示。考虑不同惯量比因素时,电池翼惯量取常值,因此虚线为水平线。由图6看出,①系统频率随本体与电池翼惯量比增大而减小,频率变化率随惯量比增大而快速变缓;②系统频率始终高于电池翼根部约束状态频率。

图6 系统频率随星体及柔性附件惯量比变化Fig.6 The change of system frequencywith theinertia ratio between system andflexible annex
5结论
通过介绍科学计算程序MATLAB与有限元分析程序NASTRAN的集成方法,实现多附件、多姿态的复杂构型航天器系统模态快速分析; 通过研究不同附件布局、姿态角及本体与附件质量/惯量比对航天器整器频率影响,获得若干影响规律,且具有实际工程设计应用价值,结论如下:
(1)可减少计算系统模态的人工干预,提高计算可靠性,有效缩短设计时间;可针对柔性附件进行不同姿态角度遍历,计算出航天器最低系统频率,为控制系统设计提供更可靠有效的频率特性参数。
(2)可通过主动调整柔性附件姿态角度改变航天器系统模态频率,实现航天器某些活动部件自转频率与系统低阶模态错频,减缓航天器内活动部件周期性转动工作时与柔性附件的自激振耦合程度。
致谢:本项目获得闵行区领军人才“空间站组建用转位机械臂研究”项目专项资金资助,在此表示感谢!
参 考 文 献
[1] 李淑娟,王皓,黄涛,等. 太阳帆板振动诱导空气流场分析及其附加质量计算[J]. 复旦学报:自然科学版,2000,39(4): 441-445.
LI Shu-Juan, WANG Hao, HUANG Tao,et al. Analysis of air flow and added mass induced by vibration of solar array[J]. Journal of FudanUniversity:Natural Science, 2000,39(4): 441-445.
[2] 郭其威,张美艳,唐国安. 太阳能电池阵地面模态试验的重力影响及其校正方案[J].振动与冲击,2008,27(12):44-46.
GUO Qi-wei, ZHANG Mei-yan, TANG Guo-an.The influence of gravity on solararray modalexperiment andcorrection scheme[J]. Journal of Vibration and Shock, 2008,27(12):44-46.
[3] 李东旭.挠性航天器结构动力学[M].北京:科学出版社,2010.
[4] 章仁为.卫星轨道姿态动力学与控制[M]. 北京:北京航空航天大学出版社,1998.
[5] 徐小胜,于登云,曲广吉.柔性航天器自由飞行状态系统基频的估算方法[J].宇航学报, 2004, 25(2):208-212.
XU Xiao-sheng, YU Deng-yun, QU Guang-ji. The natural frequency calculating for flexible spacecraft in free flight[J]. Journal of Astronautics,2004, 25(2):208-212.
[6] 王勖成,邵敏.有限单元法基本原理和数值方法[M].北京:清华大学出版社,2002.
[7] 盛宏玉.结构动力学[M].安徽:合肥工业大学出版社,2005.
The effect and change rule of spacecraft flexible annex on system natural vibration characteristics
GUOQi-wei1,2,WUSong1,2,LIUFang1,2,TANGGuo-an3
(1. Shanghai Key Laboratory of Space Structure Institutions, Shanghai 201108, China;2. Aerospace Systems Engineering Shanghai, Shanghai 201109, China;3. Department of Mechanics and Engineering, Fudan University, Shanghai 200433, China)
Abstract:A structural dynamics method for rapidly solving spacecraft system modes with large flexible appendages was introduced. By scanning the system modes of the appendages in all possible working attitudes, the system mode’s computing efficiency was significantly improved by reducing several flexible appendages in the model, largely reducing freedom, and carrying out combined simulation analysis with integrating MATLAB and NASTRAN. Through simulations by using the rapid solution method, the influence on constrained modes with flexible appendages and system modes were clarified by three aspects: the system configuration of the spacecraft, the rotation angle of the flexible appendages, and the mass and inertia ratio between the spacecraft and the flexible appendages.
Key words:spacecraft; flexible annex; vibration; frequency
中图分类号:O242.21
文献标志码:A
DOI:10.13465/j.cnki.jvs.2016.06.034
通信作者唐国安 男,教授,博士生导师,1962年10月生
收稿日期:2014-10-29修改稿收到日期:2015-03-25
第一作者 郭其威 男,硕士,1981年5月生
