基于开裂能密度及裂纹扩展特性的橡胶隔振器疲劳特性预测
2016-04-27王小莉上官文斌曾祥坤段小成
王小莉, 上官文斌, 曾祥坤, 段小成,3, 阎 礁
(1.广东技术师范学院 汽车学院,广州 510665; 2. 华南理工大学 机械与汽车工程学院,广州 510640;3. 宁波拓普集团股份有限公司,浙江 宁波 315800; 4. 泛亚汽车技术中心有限公司,上海 201201)
基于开裂能密度及裂纹扩展特性的橡胶隔振器疲劳特性预测
王小莉1,2, 上官文斌2, 曾祥坤1, 段小成2,3, 阎礁4
(1.广东技术师范学院 汽车学院,广州510665; 2. 华南理工大学 机械与汽车工程学院,广州510640;3. 宁波拓普集团股份有限公司,浙江 宁波315800; 4. 泛亚汽车技术中心有限公司,上海201201)
摘要:基于开裂能密度的连续介质力学参数及橡胶材料裂纹扩展特性(裂纹扩展速率与撕裂能之关系),获得橡胶部件多轴疲劳特性计算公式,并计算某汽车动力总成橡胶隔振器的疲劳特性。计算与试验对比表明,橡胶隔振器疲劳特性预测(寿命、开裂位置及开裂方向)与实测较一致。预测疲劳寿命分布在实测疲劳寿命的1/2倍分散因子内,满足工程疲劳寿命预测要求。提出的橡胶隔振器多轴疲劳特性预测方法,可用试验效率较高、投入较少的材料裂纹扩展试验代替耗时较多的材料疲劳破坏试验,不仅能为橡胶部件前期疲劳设计提供参考,亦能大幅缩短产品疲劳设计周期。
关键词:橡胶隔振器;开裂能密度;撕裂能;疲劳特性;预测
橡胶隔振器为汽车动力总成常见的重要隔振元件,由金属、橡胶材料复合而成。橡胶隔振器疲劳失效主要为基体橡胶部分[1]。据疲劳断裂机理,疲劳全寿命分为裂纹萌生寿命及裂纹扩展寿命。传统计算橡胶疲劳全寿命方法为分别计算裂纹萌生、扩展寿命后求和获得。基于裂纹萌生法计算裂纹萌生寿命时,选定的损伤参量与连续介质力学相关;裂纹扩展寿命计算采用断裂力学理论,通过材料裂纹扩展特性及给定载荷下材料对应的撕裂能,积分求得裂纹扩展寿命。撕裂能计算一般通过有限元软件对裂纹区域进行精细网格划分。而裂纹萌生法及裂纹扩展法各有优缺点[2]:用裂纹萌生法进行橡胶部件疲劳寿命预测时需借助大量疲劳破坏试验获取材料不同载荷下疲劳寿命曲线[3-4];用裂纹扩展法预测橡胶部件疲劳寿命时须已知初始裂纹尺寸并通过有限元软件计算不同宏观疲劳载荷下带裂纹体的撕裂能[5-6]。Le Cam等[7-8]由宏观、微观尺度分析载荷形式对橡胶试件疲劳裂纹形成影响。通过对橡胶疲劳损伤过程分析发现,传统意义的“裂纹萌生”可认为毛坯材料中微小瑕疵逐渐扩展。因此,设定初始裂纹尺寸为毛坯材料瑕疵尺寸时可用裂纹扩展法进行橡胶疲劳全寿命预测。Mars[9]提出的开裂能密度(Cracking energy density)可近似表示不同宏观疲劳载荷作用的橡胶材料撕裂能。
本文基于开裂能密度连续介质力学参数计算多轴载荷的橡胶撕裂能,结合橡胶材料裂纹扩展试验获得裂纹扩展特性及橡胶部件多轴疲劳寿命预测方法,并用于某橡胶隔振器疲劳寿命预测。结果表明,采用该方法对橡胶隔振器疲劳特性预测结果与实测较一致,且避免橡胶材料疲劳破坏试验。
1基于开裂能密度、裂纹扩展特性的橡胶多轴疲劳预测
1.1橡胶撕裂能与开裂能密度关系
单轴载荷的橡胶材料中全部应变能密度用于驱动裂纹开裂、扩展,此时撕裂能与应变能密度及裂纹尺寸乘积成正比。而多轴载荷下并非应变能密度全部用于驱动裂纹开裂及扩展,实际用于全驱动裂纹扩展的部分应变能称为开裂能密度。多轴载荷的橡胶撕裂能与开裂能密度Wc与裂纹尺寸a乘积成正比[10],即橡胶材料撕裂能可近似满足
T=2kWca
(1)
式中:k为与应变水平相关的系数,其近似表达式[11]为
(2)
式中:εmax为最大主应变,与最大主伸长率λmax满足关系式εmax=λmax-1。
已知宏观载荷对应橡胶材料的开裂能密度Wc[12]时,即可利用式(1)计算不同载荷橡胶材料对应的撕裂能T。
1.2橡胶多轴疲劳寿命的计算公式
橡胶材料裂纹扩展速率da/dN与撕裂能峰值Tmax满足关系式[13]为
(3)
式中:rc为与临界撕裂能Tc对应的裂纹扩展速率称为临界裂纹扩展速率,rc及Tc均表征与疲劳有关的材料属性。对同一材料保持不变;rc,Tc,F0由橡胶材料裂纹扩展试验获得。
将式(1)代入式(3)并积分,得橡胶多轴疲劳寿命Nf计算式为
(4)
式中:kWc,max为参量,对应施加的多轴疲劳载荷,与材料面有关,Wc,max为开裂能密度峰值。
已知橡胶材料的裂纹扩展特性参数rc、Tc、F0后,为求得橡胶材料多轴疲劳寿命Nf,还需获知初始裂纹尺寸a0及最大许用裂纹尺寸af,通常af远大于a0。由式(4)知,af≫a0时疲劳寿命主要由a0决定,而af的具体取值对疲劳寿命计算结果影响较小。通常af=1 mm。
对具体橡胶部件,不可能人为给产品预设初始裂纹。将式(4)用于实际橡胶隔振器疲劳寿命预测时,需确定橡胶材料固有的裂纹尺寸a0,再计算橡胶部件各材料点、面的疲劳寿命,并选最小的Nf为该橡胶部件疲劳寿命,其对应材料点、面方位为疲劳开裂的位置及方向。
2橡胶隔振器初始裂纹尺寸确定
实际的橡胶部件并非完美无缺。为确定橡胶材料中固有裂纹尺寸,用单轴拉伸疲劳载荷的实测疲劳寿命为基础。由于裂纹萌生为毛坯材料中固有裂纹逐渐扩展到可见微小裂纹过程,故用橡胶材料的裂纹扩展特性曲线预测单轴拉伸疲劳寿命。简单拉伸载荷的开裂能密度Wc与应变能密度W大小相等,因此撕裂能峰值Wc,max可由应变能密度峰值Wmax计算获得。将Wc,max=Wmax代入式(4),得单边缺口简单拉伸试件的疲劳寿命计算式为
(5)
由式(5)得
(6)
已知橡胶材料的疲劳特性参数rc、Tc、F0及疲劳载荷(kWmax与所加疲劳载荷对应)时,可由式(6)求得与每一疲劳寿命Nf对应的初始裂纹尺寸a0(令af=1 mm)。
3应用举例
以图1某结构动力总成橡胶后隔振器为例,说明橡胶隔振器多轴疲劳寿命预测方法。该隔振器为V形双主簧结构,金属内管通过键与动力总成连接,金属外管通过缩径工艺压入带安装孔的钣金管件通过钣金管件与副车架连接。其中1为限位块,2为主簧,3为金属外管,4为金属内管。为定义隔振器在汽车的安装方位,引入汽车坐标系O-XYZ及局部坐标系O-uvw。其中O-XYZ的X正向水平指向汽车后方,Z向垂直向上;隔振器局部坐标系O-uvw的u轴与汽车坐标系Z轴夹角为35°。

图1 橡胶隔振器安装方位Fig.1 The configuration ofthe rubber isolator
对防振橡胶材料进行疲劳裂纹扩展试验,数据分析所得裂纹扩展特性参数分别为rc=3.665 0×10-5m/次,Tc=17 400.7 J/m2,F0=2.333 62。为利用式(4)计算防振橡胶疲劳寿命,需确定其等效的初始裂纹尺寸。
3.1橡胶隔振器初始裂纹尺寸计算
哑铃型简单拉伸试件疲劳试验过程见文献[1],各工况实测疲劳寿命见表1。共进行10个不同应变峰值水平的疲劳试验,每工况实测20个橡胶试件。据实测工程应力-应变数据,拟合获得应变能峰值Wmax与所加应变峰值εmax满足的关系式为
Wmax=0.588 9(εmax)1.523 3
(7)
将表1中每一应变峰值εmax代入式(2)、(7)分别计算获得应变能峰值Wmax及系数k;再将二者及每工况对应实测疲劳寿命代入式(6),获得与实测疲劳寿命(最小值Nf,min、最大值Nf,max及平均值Nf,m)对应的初始裂纹长度(a0,max、a0,min、a0,m)。对所有工况的初始裂纹尺寸求算术平均,得该橡胶毛坯材料中等效裂纹长度a0=4.1897×10-5m。
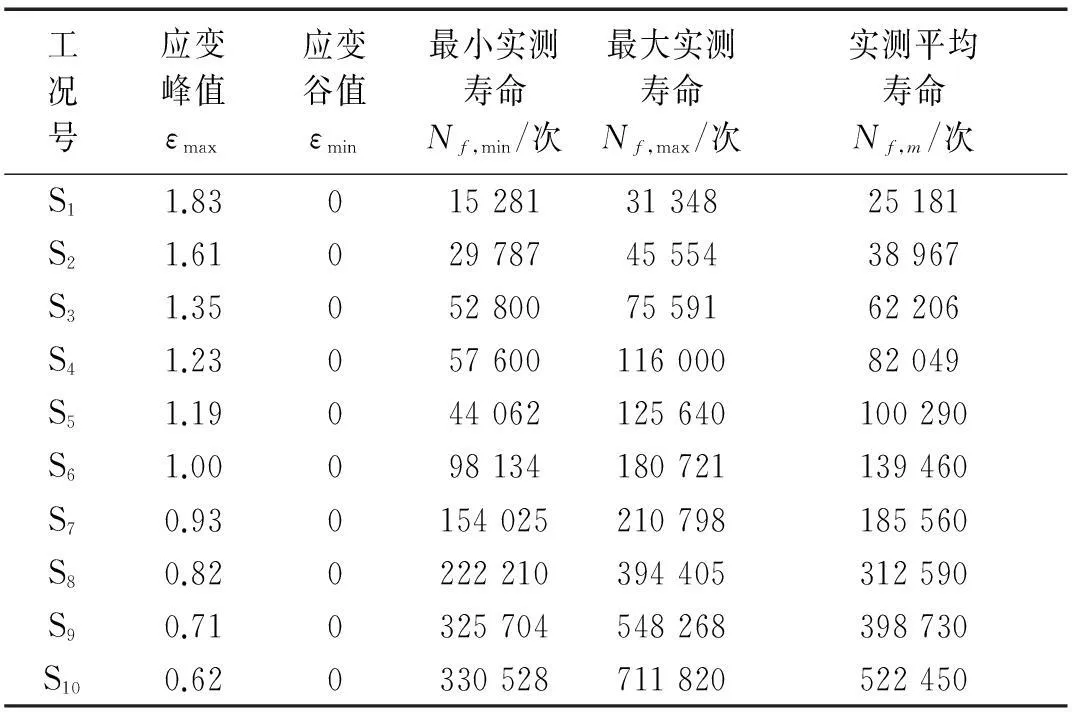
表1 哑铃型试片单轴拉伸实测与预测疲劳寿命对比
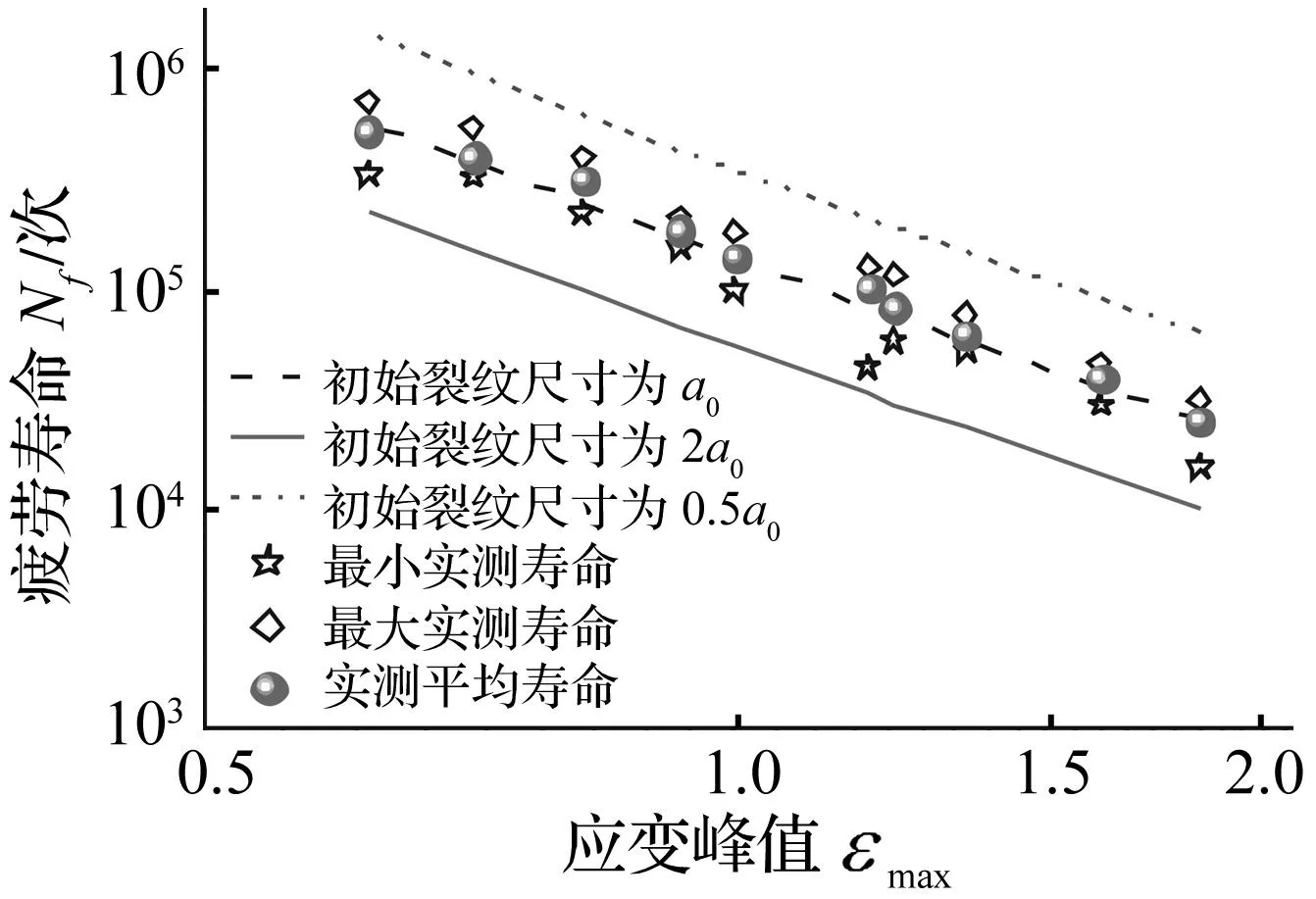
图2 不同应变峰值载荷下计算、实测疲劳寿命对比Fig.2 Comparisons of the calculated and the measured fatigue life under loads with different strain peak
为进一步说明等效初始裂纹尺寸的合理性,将a0=4.189 7×10-5m代入式(6),计算获得对应工况的疲劳寿命,并与实测对比,见图2。由图2可知,以a0=4.189 7×10-5m为初始裂纹计算所得预测寿命与实测寿命一致性较好,均分布在两倍分散线内。因文献[2]中常见橡胶材料原始缺陷尺寸一般分布于20×10-6~60×10-6m,由此可认为a0=4.189 7×10-5m合理。
3.2橡胶隔振器多轴疲劳特性预测
疲劳裂纹萌生源于材料局部变形状态,而实际橡胶部件局部多处于多轴载荷。该橡胶隔振器受Z向宏观载荷时失效点局部所受应力状态见图3。由图3可知,由于橡胶隔振器形状复杂性,即便施加在隔振器的宏观载荷为单一方向(如Z向),但局部所受三个主应力总不为0,即处于三轴应力状态,此时疲劳失效属于多轴疲劳问题。
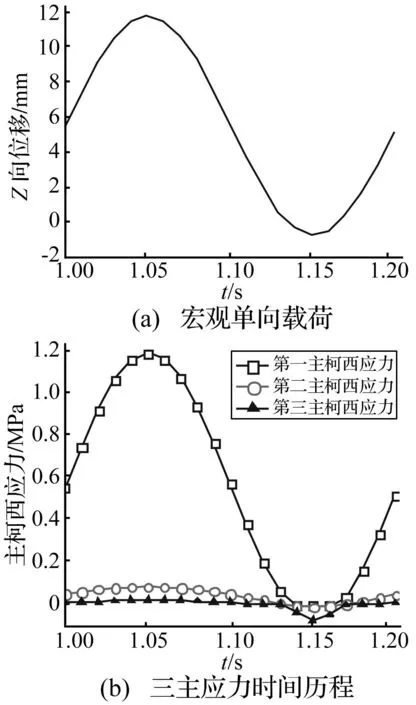
图3 宏观单向载荷下橡胶部件局部三轴应力状态Fig.3 The local triaxial stress state of rubber isolators under global loads with one direction
为求解多轴疲劳载荷对应的开裂能密度时间历程,借助有限元软件ABAQUS计算橡胶部件在宏观载荷下各点变形梯度及静水应力并作为开裂能密度计算输入,进而求解开裂能密度时间历程。基于求解的开裂能密度时间历程代入式(4),计算每工况的疲劳特性(寿命、失效位置、开裂方位),结果见表2。由计算所得每工况预测寿命与实测平均寿命(取重复测试三次的平均值)对比知,实测平均寿命与预测寿命的分散因子小于2,即预测寿命分布在实测平均疲劳寿命1/2倍分散因子内,故疲劳寿命预测精度满足工程疲劳预测要求。

表2 橡胶隔振器多轴疲劳预测疲劳特性与实测疲劳特性对比(开裂方位与Y轴夹角为90°)
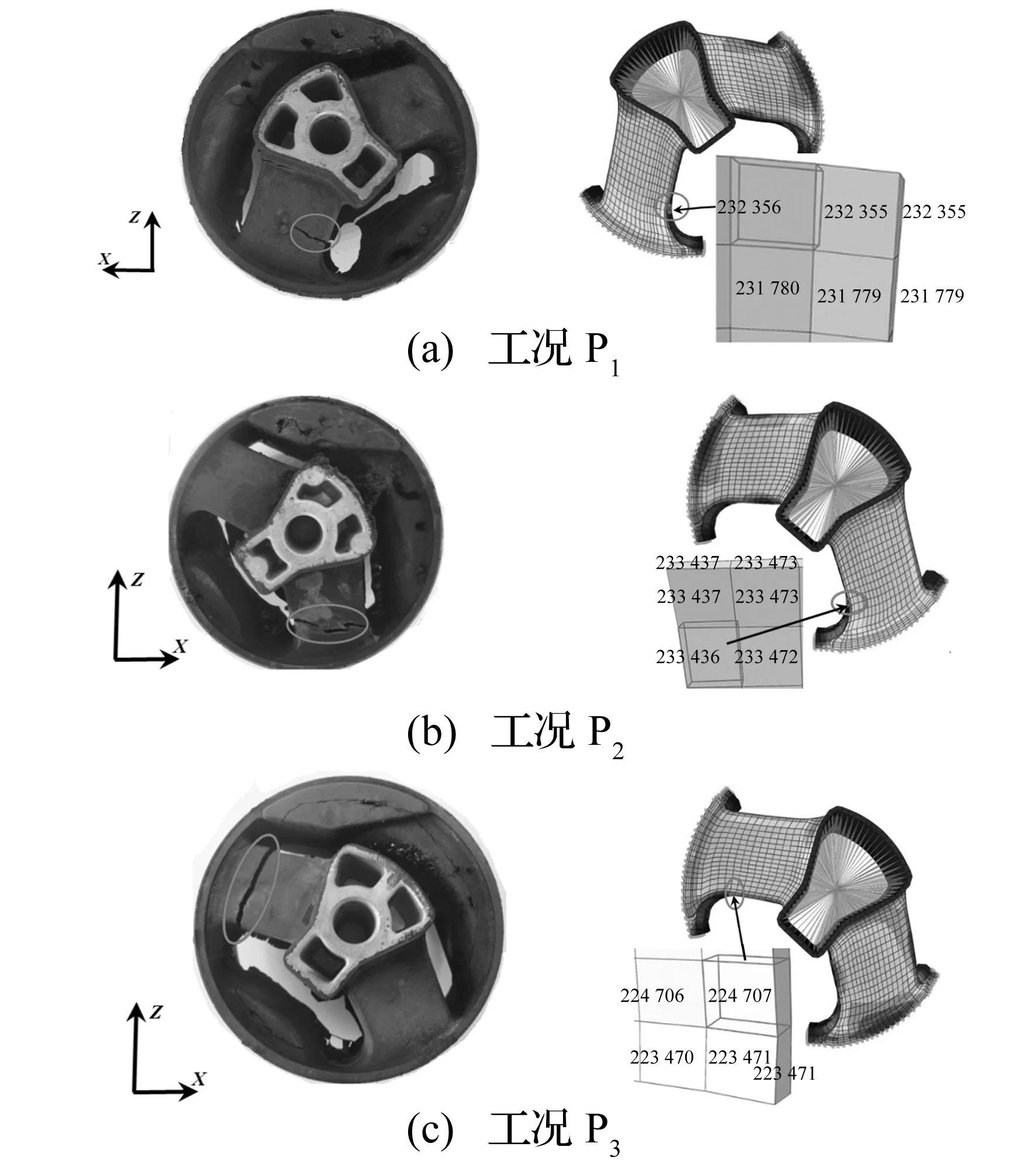
图4 橡胶隔振器实测疲劳开裂位置、方位与预测结果对比Fig.4 The comparisons of the measured and the predicted fatigue crack locations and orientations for the rubber isolator
各工况橡胶隔振器疲劳失效位置、预测结果与实测结果对比见图4。其中图4左侧为实际疲劳失效位置,右侧为预测疲劳失效位置。由对比分析知,实测疲劳失效位置与预测失效位置较一致。各工况实测开裂方位与预测较吻合,即宏观载荷为Z向时橡胶隔振器在危险位置偏于沿Z向发生开裂(开裂面法向偏向垂直于X轴);宏观载荷为X向时橡胶隔振器在危险位置偏于沿X向发生开裂(开裂面法向偏向垂直Z轴)。由于本文方法通过计算尽可能多潜在材料面的疲劳损伤预测最终开裂方位,即材料面对应疲劳损伤最大平面则为最终预测开裂面。由此可见,预测开裂面准确与否,与开裂能密度是否能完全表征疲劳损伤密切相关。实际上开裂能密度计算中未考虑橡胶疲劳裂纹闭合效应影响。因此,对表2中三种预压缩位移工况,开裂方位预测结果存在较大偏差,三种工况对应偏差分别为13°、11°及27°。总体而言,本文橡胶多轴预测方法能预测橡胶隔振器疲劳寿命、失效位置及开裂方位,可为橡胶隔振器前期疲劳设计提供参考。
4结论
(1) 基于开裂能密度及材料裂纹扩展特性可预测橡胶隔振器的多轴疲劳寿命、开裂位置及开裂方位;基于橡胶多轴疲劳寿命方法预测的寿命分布在实测寿命1/2倍分散因子内,能满足工程疲劳实际要求;预测的开裂位置、开裂方向与实测较一致。
(2)橡胶隔振器多轴疲劳特性预测方法可用于橡胶隔振器前期疲劳设计,较传统疲劳破坏试验能节省大量材料、缩短试验周期。
参 考 文 献
[1] 王小莉,上官文斌,刘泰凯,等. 填充橡胶材料单轴拉伸疲劳试验及疲劳寿命模型研究[J]. 机械工程学报,2013,49(14):65-73.
WANG Xiao-li,SHANGGUAN Wen-bin,LIU Tai-kai,et al. Experiment of uniaxial tension fatigue and modeling of fatigue life for filled natural rubbers [J]. Journal of Mechanical Engineering,2013,49(14):65-73.
[2] Mars W V, Fatemi A. A literature survey on fatigue analysis approaches for rubber [J]. International Journal of Fatigue,2002,24:949-961.
[3] Kim W D,Lee H J,Kim J Y,et al. Fatigue life estimation of an engine rubber mount [J]. International Journal of Fatigue,2004,26:553-560.
[4] Luo R K,Mortel W J,Wu X P. Fatigue failure investigation on anti-vibration springs [J]. Engineering Failure Analysis,2009,16:1366-1378.
[5] 丁智平,陈吉平,宋传江,等. 橡胶弹性减振元件疲劳裂纹扩展寿命分析[J]. 机械工程学报,2010,46(22):58-64.
DING Zhi-ping,CHEN Ji-ping,SONG Chuan-jiang,et al. Analysis of fatigue crack growth life for rubber vibration damper [J]. Journal of Mechanical Engineering,2010,46(22):58-64.
[6] Asare S, Busfield J J C. Fatigue life prediction of bonded rubber components at elevated temperature [J]. Plastics, Rubber and Composites,2011,40(4):194-200.
[7] Le Cam J B, Huneau B, Verron E. Description of fatigue damage in carbon black filled natural rubber [J]. Fatigue & Fracture of Engineering Materials & Structures, 2008, 31: 1031-1038.
[8] Le Cam J B, Huneau B, Verron E. Fatigue damage in carbon black filled natural rubber under uni-and multiaxial loading conditions [J]. International Journal of Fatigue,2013,52:82-94.
[9] Mars W V. Cracking energy density as a predictor of fatigue life under multiaxial conditions [J]. Rubber Chemistry and Technology,2002,75(1):1-17.
[10] At-Bachir M,Mars W V, Verron E. Energy release rate of small cracks in hyperelastic materials [J]. International Journal of Non-Linear Mechanics,2012,47:22-29.
[11] Gent A N,Lindley P B, Thomas A G. Cut growth and fatigue of rubbers. I. the relationship between cut growth and fatigue [J]. Journal of Applied Polymer Science,1964,8:455-466.
[12] 王小莉. 橡胶隔振器多轴疲劳寿命预测方法研究[D]. 广州:华南理工大学,2014.

A method to predict fatigue performances of rubber isolator based on the cracking energy density and the fatigue crack growth characteristic of rubber material
WANGXiao-li1,2,SHANGGUANWen-bin2,ZENGXiang-kun1,DUANXiao-cheng2,3,YANJiao4
(1. School of Automotive Engineering, Guangdong Polytechnic Normal University,Guangzhou 510665,China;2. School of Mechanical and Automotive Engineering,South China University of Technology,Guangzhou 510640,China;3. Ningbo Tuopu Group Co., Ltd.,Ningbo 315800,China;4. Pan Asia Technical Automotive Center Co., Ltd.,Shanghai 201201,China)
Abstract:A method for predicting rubber isolators’ fatigue performances including fatigue life, failure location and crack orientation was proposed. The cracking energy density and the fatigue crack growth characteristic of the studied rubber material were used in the proposed method. A typical type of rubber isolator was taken as an application subject so as to validate the proposed formula. The comparisons of the calculated and the measured results (fatigue life, failure location and crack orientation) reveal an acceptable consistence between them. Especially, the predicted fatigue life falls within a scattering factor of 1/2 of the experimental life, which is acceptable in engineering. The proposed method for predicting fatigue performances, which needs fatigue crack growth experiment instead of the traditional fatigue experiment that costs a lot of rubber materials, can give a direct guideline for fatigue-proof design of rubber isolators.
Key words:rubber isolator; cracking energy density; tearing energy; fatigue performance; prediction
中图分类号:U461.7+1;U465.4+2
文献标志码:A
DOI:10.13465/j.cnki.jvs.2016.06.012
收稿日期:2015-03-26修改稿收到日期:2015-09-09
基金项目:广东省自然科学基金(2014A030310125);国家自然科学基金(51505091);中国博士后科学基金(2015M572305)
第一作者 王小莉 女,博士后,讲师,1986年1月生
E-mail:mexlwang@scut.edu.cn
