基于近场动力学方法的混凝土板侵彻问题研究

顾　鑫， 章　青， 黄　丹

(河海大学 力学与材料学院，南京　211100)



基于近场动力学方法的混凝土板侵彻问题研究

顾鑫， 章青， 黄丹

(河海大学 力学与材料学院，南京211100)

摘要：由于近场动力学(Peridynamics)用统一空间积分-时间微分方程描述物体连续或不连续区域，改进常用微观弹脆性模型(Prototype Microelastic Model, PMB)对势本构力函数，给出刚性体与变形体冲击问题接触算法；编制计算程序，验证经典简支梁变形及Kalthoff-Winkler试验；数值模拟刚性弹丸侵彻混凝土矩形板破坏过程，揭示损伤累积及裂纹扩展全过程与最终破坏形态。结果表明，改进的近场动力学模型及算法合理、可靠，能有效模拟混凝土结构冲击破坏及侵彻问题。

关键词：混凝土板；刚性冲击；近场动力学；改进PMB模型；非局部模型；裂纹模式

混凝土结构广泛用于工业、民用及军工，为防止混凝土结构受摧毁性打击、遭破坏后及时修复，需对弹丸冲击、侵彻混凝土结构的破坏过程深入研究[1]。混凝土结构受冲击、侵彻等动荷载时产生的损伤、破坏过程即结构从连续体到非连续体的转变过程[2-3]。试验作为弹丸侵彻问题的研究方法往往耗资巨大，部分数据不易获得，难以准确观察冲击现象细微过程。而数值计算成为研究侵彻问题的重要方法。传统分析方法较难处理如静动力裂纹扩展、冲击破坏等不连续问题。研究表明，近场动力学以非局部、非连续特点，在分析不连续问题中具有巨大优势。

近场动力学(Peridynamics)方法作为非局部作用理论[4-5]，不再基于连续性假设与局部接触作用假设建模及通过空间微分方程求解问题，而将物体离散为空间域内一系列含材料所有物性信息、无几何联系、有质量的物质点(Material Point)，基于非局部作用思想建模，采用积分形式基本方程分析求解，适用于物体连续或不连续任何区域，颇受关注。

Huang等[6]运用近场动力学方法研究均质混凝土板的拉压破坏问题。沈峰等[7]对有限元法(FEM)、有限差分法(FDM)、无网格方法(MF)及离散元法(DEM)在模拟冲击侵彻问题中的优劣势进行评述，并用近场动力学方法研究刚性小球冲击混凝土板的破坏问题，但所用本构力函数较简单。Macek等[8]用近场动力学与有限元耦合方法研究刚性球形弹丸撞击、贯穿韧性铝板问题。Demmie等[9]用近场动力学方法研究飞机撞击钢筋混凝土结构问题，通过发展近场动力学气体模型，研究炸药爆炸、弹头破碎等问题。

本文通过对近场动力学模型中微观弹脆性模型的本构力函数进行改进，给出刚性体与变形体冲击问题的接触算法，并验证简支梁受弹性变形及经典的Kalthoff-Winkler试验。对刚性弹丸侵彻混凝土矩形板的破坏过程进行详细数值模拟，获得混凝土板损伤累积、裂纹扩展直至破坏的全过程。

1基于键作用的近场动力学方法

1.1基本运动方程

由图1，x,x′为参考构型物质点坐标矢量；y,y′为t时刻构型物质点坐标矢量；u,u′为t时刻构型中物质点位移矢量；ξ为物质点位置矢量；η为物质点位移矢量，且有

y=x+u,y′=x′+u′,ξ=x′-x,η=u′-u

(1)

近场动力学理论中物质点受近场范围(Horizon)内所有其它物质点共同作用，以非局部作用积分项取代传统连续介质理论运动方程中散度算子项，得基本运动方程为

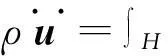
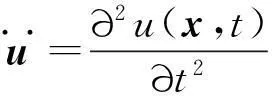
图1　物质点间相互作用及变形示意图Schematic of interaction between material points and deformation process

1.2微观弹脆性(PMB)模型

物质点间通过本构力函数作用，该函数构造为近场动力学建模首要问题。适合各向同性材料微观弹脆性模型(PMB)[10]本构力函数为

(3)

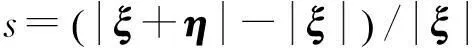
引入历史依赖标量函数μ，表征物质点对破坏

(4)

定义近场动力学损伤值为物质点近场范围内断键数与键总数之比，即

(5)

求解弹性问题时不考虑损伤产生，将s0置为无穷大；考虑破坏问题时可建立临界伸长率s0与能量释放率GF的联系，获得“键”断开的具体指标。

1.3PMB模型中改进的本构力函数

PMB模型中微观模量c为常数，无法反映长程力的空间分布规律，影响计算精度。本文提出能反映物质点间长程力基本特性的本构力函数。近场动力学本构力函数需满足的基本性质为：①递减变化规律，即本构力值随物质点间相对距离增大而减小；②有限值，即点对极限距离趋于零时本构力达有限最大值，近场范围边界达零值，近场区域外为零；③对称性，即本构力服从作用力与反作用规律。

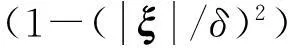
以三维问题为例，构型在各向均匀拉伸荷载作用下发生纯体积改变时，有各向均匀应变ε1=ε2=ε3=ε0，此时弹性应变能密度为

(6)

变形状态对应的近场动力学中有s=ε0，以球坐标形式表示的应变能密度为

(7)

由VV,el=VV,pd，推导得

(8)

同三维模型推导过程，对二维平面应力问题(单位厚度)，推导得

(9)

式中：λ,G为拉密常数；E为弹性模量；ν为泊松比；w为发生位移时一个“键”存储的能量密度。

2近场动力学方法数值实现

2.1局部阻尼引入

为利用近场动力学方法求解准静力问题，考虑传统动力学的动态松弛法，在运动方程中引入局部阻尼项[12]，即

(10)

式中：C为人工阻尼系数，大小主要影响求解收敛速度、收敛方式，但对定量计算精度影响不大；其它变量同前。

2.2离散形式

按近场动力学方法进行空间离散，对节点xi考虑近场范围内(‖xp-xi‖≤δ)的相互作用，动力学基本方程离散为

(11)

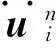
(12)

(13)

(14)

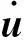
2.3刚性体与非刚性体冲击接触算法

研究刚性弹丸冲击变形体时，为实现冲击接触作用且不发生弹丸与靶体相互渗透，采用以下方法[11]：

刚性弹丸初速度为v0，靶体变形遵循近场动力学运动方程；靶体物质点位置更新滞后于弹丸运动，接触后弹丸与靶体发生渗透；为反映冲击接触真实物理过程，与弹丸叠合物质点需更新位置；更新过程将叠合物质点移动最短距离到弹丸外部，且物质点与弹丸表面距离最近，见图2。该过程反映任意时刻t弹丸与靶体间形成接触面，能刻画物体冲击接触问题。

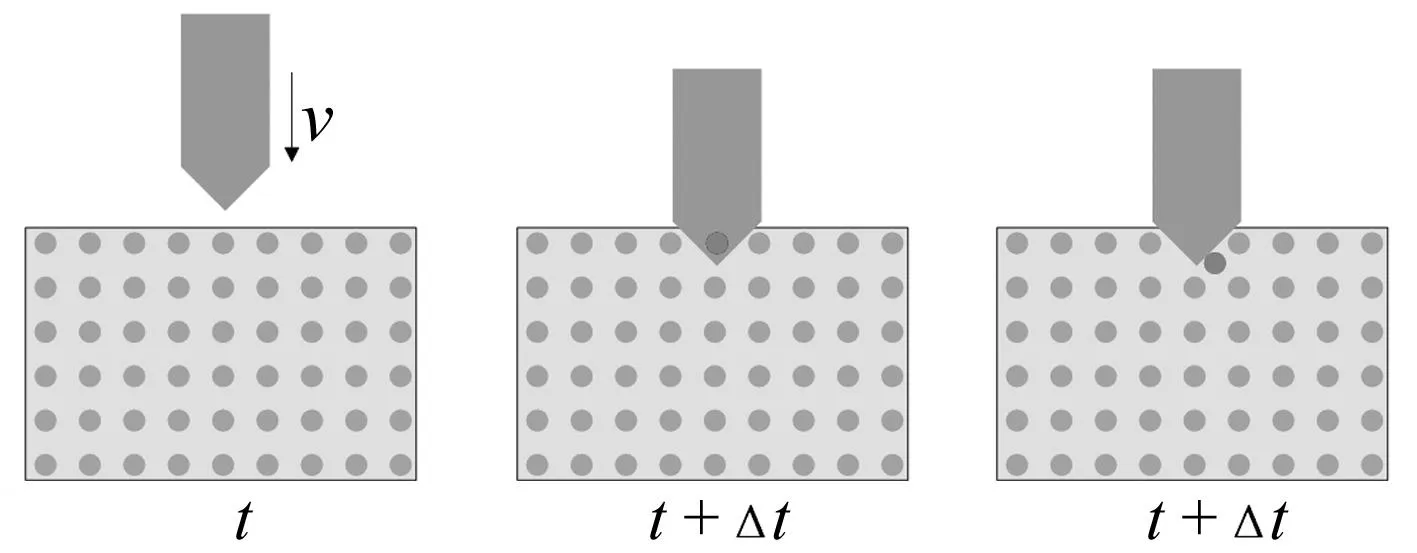
图2　刚性体与可变形体接触中物质点位置更新示意图Fig.2 Relocation of material points inside a target deformable body to represent contact with the rigid projectile

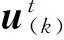
(15)

t+Δt时刻物质点xk对弹丸作用力为

(16)

t+Δt时刻弹丸所受合力为

(17)

2.4物质点间短程排斥力

模拟靶体物质点运动状态时为防止靶体物质点出现相互渗透等非物理变形现象，需增加短程排斥力项，即

fs(y′,y)=

(18)

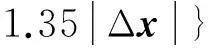
(19)

3数值验证

据近场动力学理论方法编制近场动力学计算程序，分析简支梁静力变形及Kalthoff-Winkler试验。

3.1简支梁受集中荷载作用

矩形截面简支梁在跨中受集中力作用，用本文改进的PMB二维平面应力(取单位厚度)模型分析变形。简支梁长1 m，高0.1 m；梁上边缘中点承受大小1 kN、垂直向下的集中荷载；设材料为均匀、各向同性的弹脆性材料，弹性模量E=20 GPa，泊松比υ=1/3。

静力分析中用2 mm×2 mm方形晶格均匀离散，共离散成25 551个物质点；将简支梁两端下部角隅处各约束1个物质点，左端水平、竖直向均固定；右端只约束竖直向位移，在上表面中点处物质点施加集中力1 kN；显式动力迭代时间步长取Δt=4×10-7s，人工阻尼系数为C=106，共计算4万步。

为便于比较、验证本模型计算结果的准确性，有限元解、具有常微观模量的PMB解、本文解及理论解所得梁中性轴竖向位移分布曲线见图3。由图3可知，PD解与理论解吻合良好，计算误差小于有限元解，较常微观模量PMB模型，本文改进的PMB模型计算结果更接近理论解。

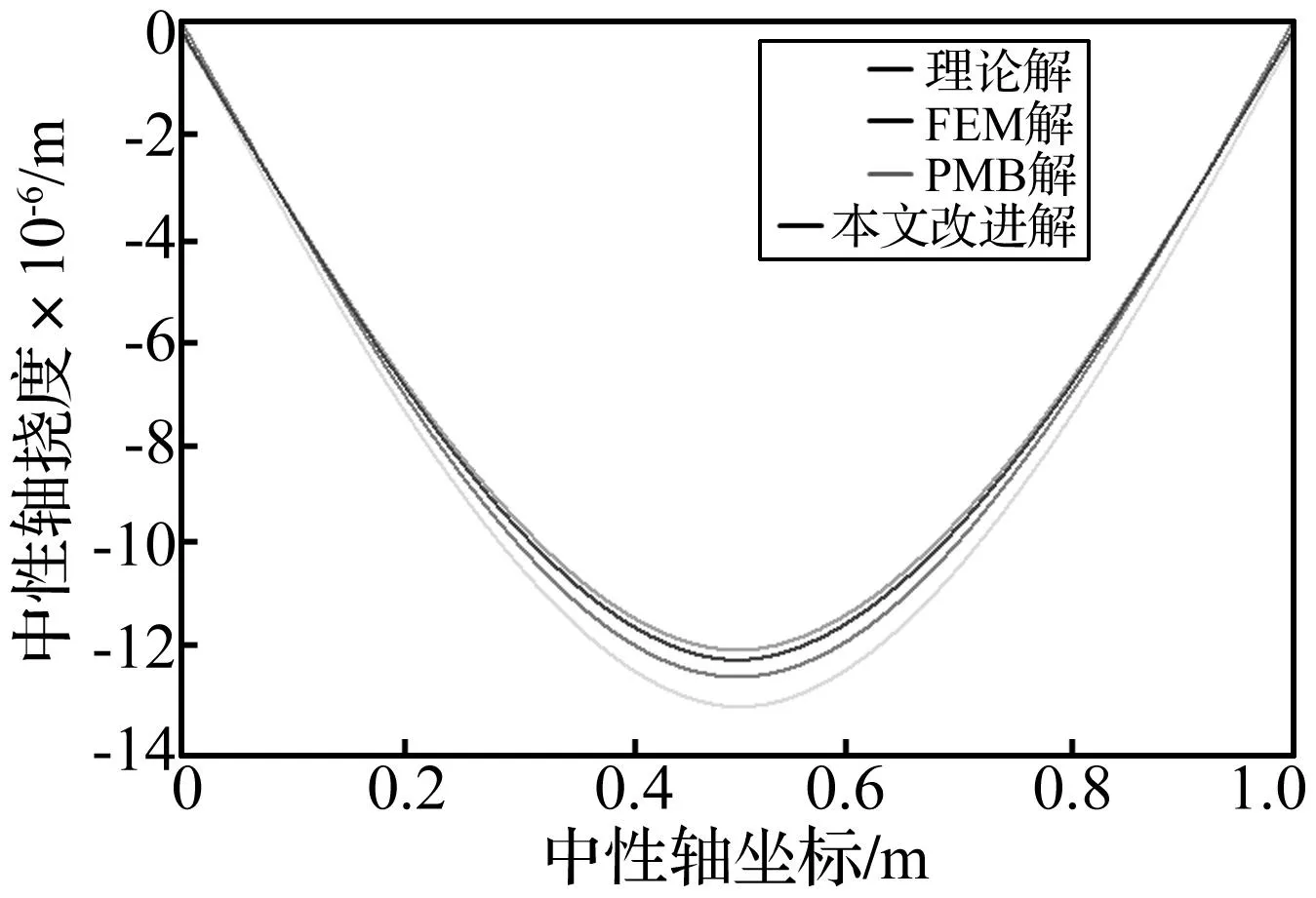
图3　简支梁中性轴挠度曲线Fig.3 Deflection of neutral axis of simply supported beam

3.2三维Kalthoff-Winkler试验[14-15]

该试验用刚性柱体撞击马氏体时效钢靶，为典型的动力断裂问题，几何模型见图4(a)。马氏体时效钢指以无碳或微碳的铁镍马氏体为基体，经时效能产生金属间化合物沉淀硬化的超高强度钢[16]，具有强度高、断裂韧性强、高温力学性能优异、表面硬度及疲劳极限高等力学性能。试验结果表明，刚性柱体撞击马氏体时效钢靶体时产生压缩应力波，并与裂尖相互作用，产生ΙΙ型开裂，恰当选取撞击速度可从裂尖起裂，发生剪切与拉伸混合型开裂，形成约68°的裂纹扩展角。能否成功模拟该试验已成为判断数值方法对脆性材料动力断裂问题适用性手段。本文选材料弹性模量E=191 GPa，泊松比υ=1/4，质量密度ρ=8 000 kg/m3，材料临界伸长率取s0=0.015；刚性柱体弹丸质量m=1.57 kg，初速度为-32 m/s。马氏体时效钢共均匀离散178 200个立方体晶格，尺寸1 mm×1 mm×1 mm，单晶格体积1×10-9m3；显式动力迭代时间步长取Δt=8×10-8s，共计算4千步。近场动力学模拟结果见图4(b)～4(c)。在冲击剪切作用下预制裂纹裂尖产生损伤，累积到一定程度后发生裂尖起裂并在剪切与拉伸共同作用下不断开裂，形成约67°扩展角的裂纹。以损伤值φ=0.35作为开裂判据，裂纹起裂时间约为28.56 μs，扩展完成时间为91.52 μs，试验获得起裂时间略低于29 μs；PD模拟与试验所得裂纹起裂时间、扩展角高度一致。

该问题的瑞利波速(Rayleigh Wave Speed)为2 799.2 m/s，PD模拟的裂纹传播速度与其它数值方法模拟结果[17-18]见图5。由图5看出，因物质点尺寸较大，PD模拟计算的波速波动较大，但与其它两种数值方法总体趋势一致。

以上分析表明，PD方法能较好刻画马氏体时效钢的裂纹扩展、撞击破坏全过程，亦验证近场动力学方法在模拟动力断裂问题的适用性。

图4　Kalthoff-Winkler试验Fig.4 Kalthoff-Winkler experiment

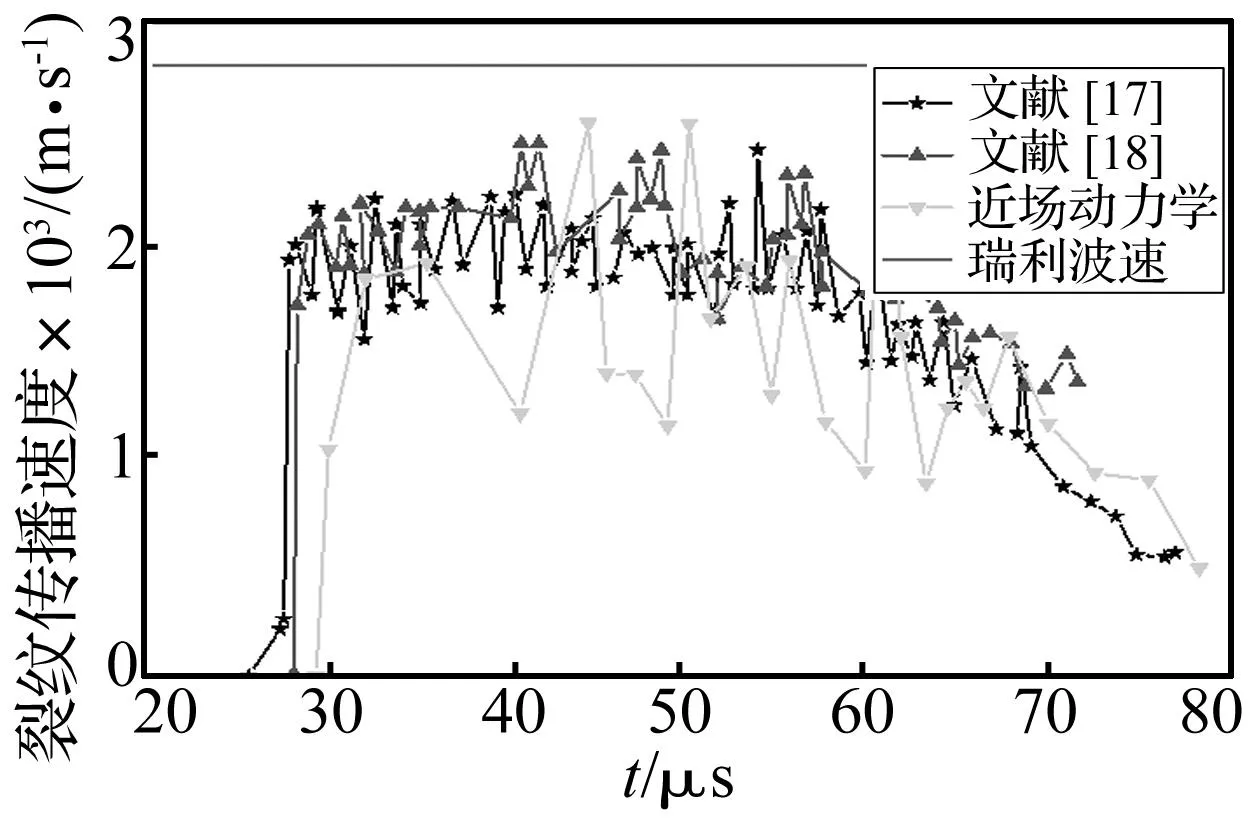
图5　马氏体时效钢裂尖传播速度Fig.5 The crack propagation speed of Maraging steel

4刚性小球侵彻混凝土板过程模拟

用近场动力学方法及本文改进的本构力函数模拟刚性小球侵彻撞击混凝土板问题。

4.1计算模型

设混凝土为均匀、各向同性的脆弹性材料，弹性模量E=30 GPa，泊松比υ=1/4，能量释放率GF=175 MN/m，质量密度ρ=2 400 kg/m3；混凝土板几何参数：长200 mm，宽100 mm，板厚20 mm；刚性小球半径10 mm，质量密度ρ=7 800 kg/m3；小球初速度分别为10 m/s、20 m/s、50 m/s、100 m/s，垂直撞击混凝土板上表面中心。

近场动力学模型中混凝土板离散为均匀立方体晶格，尺寸2 mm×2 mm×2 mm，共离散为56 661个物质点，每个粒子体积为8×10-9m3；显式动力迭代时间步长取Δt=1×10-7s，共计算5 000步。

4.2计算结果与分析

计算所得刚性小球撞击混凝土板损伤累积、破坏渐进过程。4种不同冲击速度、侵彻初始至2 200时间步时(间隔200时步)混凝土板损伤及破坏见图6～图9。其中浅色表示损伤度为1即物质点处于完全损伤状态，深色表示损伤度为0即物质点处于无损状态。

图6　弹丸侵彻下的混凝土板损伤破坏过程(v=10 m/s)Fig.6 The damage progression of a concrete slabsubjected to rigid projectile(v=10 m/s)

图7　弹丸侵彻下混凝土板损伤破坏过程(v=20 m/s)Fig.7 The damage progression of a concrete slab subjected to rigid projectile(v=20 m/s)

图8　弹丸侵彻下的混凝土板损伤破坏过程(v=50 m/s)Fig.8 The damage progression of a concreteslab subjected to rigid projectile(v=50 m/s)

图9　弹丸侵彻下的混凝土板损伤破坏过程(v=100 m/s)Fig. 9 The damage progression of a concrete slab subjected to rigid projectile(v=100 m/s)

由4图看出，小球撞击靶板正面后产生向靶板背面传播的压缩应力波，弹着点附近呈压碎现象，产生压缩破坏漏斗(弹坑)；反射拉伸应力波与运动压缩波共同作用致物质点间作用弱化，产生锥形体(圆台体)损伤区域，并伴随大量微裂纹开裂损伤逐渐累积，随冲击过程进行裂纹扩展、贯通，形成锥形体冲切表面及冲切区域，冲切区内由于拉压应力波共同作用发生破碎出现粒子飞溅脱离现象；锥形体界面为薄弱界面，有大量微裂纹产生、扩展，贯通形成数条径向裂缝，并由锥形体表面向靶板正面扩展，扩展同时径向主裂纹发生分叉产生次级裂纹，次级裂纹与其它微裂纹共同扩展贯通为环向裂纹。

在弹丸冲击靶板问题中，靶板厚度与冲击速度不同组合会使靶板形成4种破坏形态，即冲击弹坑、冲击震塌、冲击贯穿、冲击冲切[19-20]。本例中因靶板较薄，弹丸对混凝土板皆为穿透性冲击，产生的表面弹坑与靶板背面震塌漏斗交汇，无明显冲击贯穿过程，故混凝土靶板主要表现为冲击冲切破坏形态，形成锥形体或圆台体冲切破坏区域，冲切部分内部发生大量破碎；弹着点附近发生混凝土压缩破碎、出现表面弹坑，并伴碎片粒子反向飞溅。而不同速度下冲切区域大小无显著差别，但弹坑深度及周围破碎程度受弹丸速度变化影响明显，弹坑大小与破碎程度及冲击接触区域碎片反向飞溅数量与剧烈程度均随撞击速度增大而变大。

不同冲击速度下2 400时间步时混凝土板弹着点所在面及弹丸出面破坏见图10。由图10看出，撞击速度不同混凝土板破坏形态亦不同，速度越大径向、环向裂纹数目越多，破碎程度越剧烈；弹丸出露面破坏较弹着点所在面更严重。此因弹丸在靶体内产生球面压缩波，致弹着点附近一定范围内混凝土被挤压、粉碎，而压缩波到靶板背面产生反射拉伸波，靶板出现径向、环向裂纹，裂纹贯通使部分块体从靶体脱落，形成震塌漏斗坑，产生大量粒子飞溅脱离。

图10　混凝土板受不同速度弹丸冲击作用上下表面破坏图(t=2 400)Fig.10 The top and bottom monolayers of concrete slabs showing fragmentation with different velocity (t=2 400)

定义结构所有物质点损伤值之和与物质点数目比值为该结构累积总损伤量。弹丸不同初始速度下混凝土板累积损伤变化过程见图11。由图11看出，侵彻开始时混凝土板损伤量迅速增大；弹丸速度越大损伤量越大，破坏越剧烈，损伤量增幅亦越大；随侵彻过程进行损伤量增加到一定程度后增量趋于平缓；弹丸贯穿混凝土板后损伤量仍有一定增加。速度为100 m/s时损伤量约为0.687，速度为10 m/s时损伤量仅0.164。可见，弹丸速度对靶板损伤程度影响较大，速度越大贯穿混凝土板时间越短，破坏程度越大。

图11　不同初始速度弹丸侵彻下混凝土板累积损伤变化Fig.11 The accumulated damage evolution of concrete slabs with different velocity

弹丸初速度150 m/s及200 m/s时混凝土板最终损伤量值及弹丸残余速度与不同初速度关系曲线见图12。由图12看出，弹丸初速度越大混凝土板最终损伤量值越大，破坏程度越大，且弹丸残余速度与弹丸初速度成正比。

图12　弹丸残余速度及混凝土板总损伤量与弹丸初始速度关系Fig.12 Relationship between residual velocity and initial velocity, and relationship between accumulated damage and initial velocity

5结论

通过改进近场动力学方法微观弹脆性模型，提出反映长程力空间变化规律的本构力函数，给出刚性体与变形体冲击问题接触算法，编制近场动力学计算程序，验证简支梁变形与经典Kalthoff-Winkler试验，并对刚性球形弹丸侵彻混凝土矩形板破坏过程进行数值模拟，结论如下：

(1)本文方法能获得刚性球形弹丸侵彻混凝土矩形板破坏过程，即混凝土板弹着点附近弹坑大小、混凝土破碎程度、板累积总损伤量及破坏程度均随冲击速度增大而增大。不同冲击速度下裂纹形态差异显著，低速时混凝土板裂纹数较少，且径向裂纹明显，破碎程度较低；高速时混凝土板裂纹数多、环向裂纹多、破碎程度高；弹丸残余速度与初始冲击速度成正比。

(2)对弹丸侵彻混凝土板的极限分析包括确定薄板厚度与极限贯穿速度定量关系及混凝土板背部出现剥离的极限速度等。由于目前近场动力学模型只考虑物质点对的中心作用，忽略物质点所处环境影响，故需进一步研究近场动力学状态理论[21]。本文所提方法为模拟混凝土结构冲击破坏、侵彻问题的有效方法。

参 考 文 献

[1] 刘海峰,宁建国. 冲击荷载作用下混凝土动态本构模型的研究[J]. 工程力学, 2008, 25(12):135-140.

LIU Hai-feng, NING Jian-guo. Dynamic constitutive model of concrete subjected to impact loading[J]. Engineering Mechanics, 2008, 25(12): 135-140.

[2] 刘凯欣,郑文刚,高凌天. 脆性材料动态破坏过程的数值模拟[J]. 计算力学学报, 2003, 20(2):127-132.

LIU Kai-xin,ZHENG Wen-gang,GAO Ling-tian. Numerical simulation for the dynamic failure process in brittle materials[J].Chinese Journal of Computational Mechanics,2003,20(2):127-132.

[3] 张德海,朱浮声,邢纪波. 弹丸侵彻无钢筋混凝土的数值模拟[J]. 岩土力学,2006, 27(7): 1143-1152.

ZHANG De-hai, ZHU Fu-sheng, XING Ji-bo. Numerical simulation of projectile penetrating into plain concrete[J]. Rock and Soil Mechanics, 2006, 27(7):1143-1152.

[4] Silling S A. Reformulation of elasticity theory for discontinuities and long-range forces[J]. Journal of the Mechanics and Physics of Solids, 2000, 48: 175-209.

[5] 黄丹,章青,乔丕忠,等. 近场动力学方法及其应用[J]. 力学进展, 2010, 40(4): 448-459.

HUANG Dan, ZHANG Qing, QIAO Pi-zhong,et al. A review on peridynamics method and its application[J]. Advance in Mechanics, 2010, 40(4): 448-459.

[6] Huang D, Zhang Q, Qiao P Z. Damage and progressive failure of concrete structures using non-local peridynamic modeling[J]. Science China Technological Sciences, 2011, 54(3): 591-596.

[7] 沈峰,章青,黄丹,等. 冲击荷载作用下混凝土结构破坏过程的近场动力学模拟[J]. 工程力学, 2012, 29(A01): 12-15.

SHEN Feng, ZHANG Qing, HUANG Dan, et al. Peridynamics modeling of failure process of concrete structure subjected to impact loading[J]. Engineering Mechanics, 2012, 29(A01): 12-15.

[8] Macek R W, Silling S A. Peridynamics via finite element analysis[J]. Finite Elements in Analysis and Design, 2007, 43(15): 1169-1178.

[9] Demmie P, Silling S. An approach to modeling extreme loading of structures using peridynamics[J]. Journal of Mechanics of Materials and Structures, 2007, 10(2):1921-1945.

[10] Silling S A, Askari E. A meshfree method based onthe peridynamic model of solid mechanics[J].Computers and Structures, 2005, 83(17/18), 1526-1535.

[11] Madenci E, Oterkus E. Peridynamic theory and its applications[M].Berlin:Springer, 2014.

[12] Kilic B. Peridynamic theory for progressive failure prediction in homogeneous and heterogeneous materials [D].Tucson, AZ:The University of Arizona, 2008.

[13] Parks M L, Seleson P, Plimpton S J, et al. Peridynamics with lammps: a user guide V0.3 beta[R]. Sandia National Laboratories, Albuquerque, NM, 2011.

[14] Kalthoff J F, Winkler S. Failure mode transition at high rates of shear loading[J]. DGM Informationsgesellschaft MbH, Impact Loading and Dynamic Behavior of Materials, 1988, 1: 185-195.

[15] Kalthoff J F, Bürgel A. Influence of loading rate on shear fracture toughness for failure mode transition[J]. International Journal of Impact Engineering, 2004,30(8): 957-971.

[16] 尹航,李金许,宿彦京,等. 马氏体时效钢的研究现状与发展[J]. 钢铁研究学报, 2014, 26(3): 1-4.

YIN Hang, LI Jin-xu, SU Yan-jing, et al. Curent situation and development of Maraging steel[J]. Journal of Iron and Steel Research, 2014, 26(3): 1-4.

[17] Belytschko T, Chen H, Xu J, et al. Dynamic crack propagation based on loss of hyperbolicity and a new discontinuous enrichment[J]. International Journal for Numerical Methods in Engineering,2003,58(12): 1873-1905.

[18] Song J H, Areias P, Belytschko T. A method for dynamic crack and shear band propagation with phantom nodes[J]. International Journal for Numerical Methods in Engineering, 2006, 67(6): 868-893.

[19] 宁建国,王成,马天宝. 爆炸与冲击动力学[M].北京：国防工业出版社, 2010.

[20] 董军,邓国强,杨科之,等. 弹丸对混凝土薄板的冲击破坏效应[J]. 岩石力学与工程学报, 2005, 24(4): 713-720.

DONG Jun, DENG Guo-qiang, YANG Ke-zhi, et al. Damage effect of thin concrete slabs subjected to projectile impact[J].Chinese Journal of Rock Mechanics and Engineering, 2005, 24(4): 713-720.

[21] Silling S A, Epton M, Weckner O, et al. Peridynamic states and constitutive modeling[J]. Journal of Elasticity, 2007, 88: 151-184.

Peridynamics used in solving penetration problem of concrete slabs

GUXin,ZHANGQing,HUANGDan

(College of Mechanics and Materials, Hohai University, Nanjing 211100, China)

Abstract:Peridynamics uses uniform spatial-integral and time-differential equations to describe materials and structures in both continuous and discontinuous areas. It is a nonlocal extension of continuum mechanics and a new meshfree numerical method. The pairwise constitutive function widely used in PMB model was modified, and an algorithm for impact contact between rigid projectile and deformable body was proposed. The peridynamic method was validated through the deformation of a simply supported beam and the well-known Kalthoff-Winkler experiment. Furthermore, concrete slabs subjected to rigid projectile impact were simulated. The simulation results reveal explicitly the final failure patterns of concrete slabs and the whole process of concrete failure from the damage accumulation to the final failure. The numerical simulations illustrate that the modified peridynamic model is reasonable and reliable, and peridynamics is an effective method in simulating the impact problems of concrete structures.

Key words:concrete slab; rigid impact; peridynamics; modified PMB model; nonlocal model; cracking pattern

中图分类号:O34; O347

文献标志码：A

DOI:10.13465/j.cnki.jvs.2016.06.009

通信作者章青 男，教授，博士生导师，1963年5月生

收稿日期：2014-11-19修改稿收到日期：2015-04-03

基金项目：国家自然科学基金(11372099;11132003;51179064);江苏省自然科学基金(BK20151493)

第一作者 顾鑫 男，博士生，1991年1月生