双腔结构消声器声学性能计算子域耦合方法

方　智， 季振林， 刘成洋

(1.华中科技大学 船舶与海洋工程学院，武汉　430074； 2．哈尔滨工程大学 动力与能源工程学院，哈尔滨　150001；3. 中国舰船研究设计中心，武汉　430064)



双腔结构消声器声学性能计算子域耦合方法

方智1， 季振林2， 刘成洋3

(1.华中科技大学 船舶与海洋工程学院，武汉430074； 2．哈尔滨工程大学 动力与能源工程学院，哈尔滨150001；3. 中国舰船研究设计中心，武汉430064)

摘要：提出基于子域划分的耦合方法求解双腔结构消声器声学性能。据结构特点或材料属性将消声器分为不同子域，用数值模态匹配法或三维解析方法求解规则等截面子域结构传递矩阵，用三维数值方法求解非规则渐变截面子域结构传递矩阵，用子域连续条件求得消声器整体矩阵，进而获得消声器传递损失。分别用基于子域划分的耦合方法、三维有限元方法及数值模态匹配法计算典型双腔结构消声器的传递损失。结果表明，基于子域划分的耦合方法适用预测双腔结构消声器声学特性，与数值模态匹配法相比计算效率较高。

关键词：消声器；消声特性；耦合方法；数值模态匹配法

消声器内部声场较复杂，需用三维计算方法预测消声特性。常用方法有三维解析法及三维数值法。解析方法计算精度高、速度快，仅适用横截面形状规则结构；而三维数值方法可计算任意横截面形状的消声器声学特性，但存在前处理过程复杂、计算时间长及对计算机内存要求高等缺点。因此，将解析方法与数值方法结合即半解析方法被用于计算任意形状消声器的声学特性。Kirby[1]提出用二维有限元方法求解穿孔管阻性消声器横向模态，用配点法求解消声器声学量。利用该方法计算的椭圆形同轴直通穿孔管阻性消声器传递损失结果与实验结果在1 500 Hz内基本吻合。Albelda等[2-3]利用元件模态综合法求解穿孔管阻性消声器横向模态，用模态匹配技术计算消声器声学量，表明椭圆形非同轴直通穿孔管阻性消声器的传递损失结果与实验值在所关心频率范围内吻合较好。Kirby[4]改进所提有限元-配点法，用模态匹配法代替配点法求解消声器模态幅值系数，所得椭圆形同轴直通穿孔管阻性消声器传递损失结果与实验值在1 500 Hz内吻合较好。Fang等[5-7]用数值模态匹配法对含插管、双出口管及进出口管不同轴的典型结构消声器进行计算，结果与实验值及三维有限元结果吻合较好。

由于模态匹配法及配点法的限制，半解析方法只能计算沿轴向方向等截面结构的声学特性，对渐扩或渐缩结构不适用。工程中常见的多腔消声器结构用数值模态匹配法时需求解较多方程，复杂且计算时间长。

本文将数值模态匹配法与解析方法或数值方法耦合计算此类问题，即数值模态匹配-数值/解析耦合方法。该方法基本思想为将一个复杂系统划分成多个子域单元，据每个子域结构、材料特性分别用不同方法计算传递矩阵，利用交界面的连续性条件通过矩阵运算联接各子域，求得消声器进出口交界面整体传递矩阵，进而获得消声器声学特性参数，不仅能降低计算机内存要求并可大量节省机时、提高计算速度。子域划分方法已用于结构力学[8-9]，但在管道声学领域少见。本文目的在于，①用数值模态匹配法求解消声器子域结构传递矩阵，结合连续条件求得消声器整体矩阵，进而用四极参数求得消声器传递损失；②用基于子域划分的耦合方法、数值模态匹配法及三维有限元法计算典型双腔结构消声器传递损失，通过比较验证耦合方法的正确性及高效性。

1子域划分法

用传递矩阵描述每个子域的声学特性。考察图1双级膨胀腔消声器，用子域划分法将其分隔为三个子域1、2、3，分别设子域1、2、3进出口声压及质点振速为pi，ui，po1，uo1，pi2，ui2，po2，uo2及pi3，ui3，po，uo。在交界面上，声压、质点振速连续，有

po1=pi2,uo1=ui2

(1)

po2=pi3,uo2=ui3

(2)

三个子域传递矩阵可表示为

(3)

(4)

(5)

将声压、质点振速连续性条件式(1)、(2)代入式(3)～式(5)，得整个消声器结构传递矩阵为

(6)

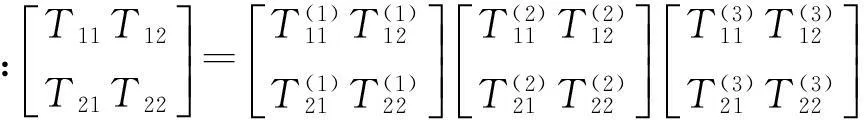
求解出每个子域的传递矩阵，整个消声器结构的传递矩阵通过简单矩阵运算即可求得。以图1消声器子域1为例，说明传递矩阵求解方法。出口给定边界条件为

uo1=0

(7)

(8)

(9)

出口给定边界条件为

po1=0

(10)

(11)

(12)

第二、三个子域传递矩阵可同理获得。

2四极参数与传递损失计算

系统进、出口为平面波声场时可由系统传递矩阵获得四极参数，进而获得消声器传递损失。消声器进出口声压与质量质点振速关系表示为

(13)

式中：A，B，C，D为四极参数。

消声器传递损失可由四极参数表示为

(14)

式中：Si，So为进、出口横截面积。

求出整个消声器结构进出口边界传递矩阵后由式(6)可求出消声器四极参数与传递矩阵关系表达式，即

(15)

将消声器四极参数代入式(14)中即可求得消声器传递损失。

3基于数值模态匹配技术的传递矩阵求解

消声器传递矩阵基于平面波理论求解，用基于平面波理论的传递矩阵法求解消声器声学特性时具有一定限制性。为获得较准确计算结果，需对消声器横截面积突变处的连接管进行长度修正。本文采用数值模态匹配法求解消声器子域的传递矩阵，由于数值模态匹配法为三维分析方法，应考虑消声器内的高阶模态效应。消声器不同子域间连接管径一般较小，在高频率范围内无高阶模态被激发，故用数值模态匹配法计算子域传递矩阵时假设进出口管道内为平面波传播。

双腔抗性消声器(图1)中1、3为进出口外插的膨胀腔结构，见图2。膨胀腔被进出口插管分为A、B、C、D、E五区域，横截面分别为SA、SB、SC、SD、SE，且SA=SE，SB=SD。本文用数值模态匹配法求解进出口边界传递矩阵。子域2为直管，用解析法求解。

图2　进出口外插膨胀腔结构示意图Fig.2 Sketch of expansion chamber with extended inlet and outlet

子域1、3各横截面横向本征方程为

(16)

式中：K，M为广义刚度、质量矩阵。

求解式(16)可得每个横截面的本征波数及本征向量，进而求得本征函数。子域1、3管道内声压、质点振速表达式为

(17)

(18)

膨胀腔进出口横截面声压、质点振速的连续及边界条件为

pC(z=0)=pA(z=0),(x,y)∈SA

(19)

pC(z=0)=pB(z=0),(x,y)∈SB

(20)

(21)

pC(z=LC)=pD(z=LC),(x,y)∈SD

(22)

pC(z=LC)=pE(z=LC),(x,y)∈SE

(23)

(24)

UB,z(z=-L1)=0,(x,y)∈SB

(25)

UD,z(z=LC+L2)=0,(x,y)∈SD

(26)

据传递矩阵求解方法，将式(17)、(18)代入式(19)～式(26)，结合式(7)、(10)，在方程两边同乘积分横截面的本征函数并且积分，利用本征函数正交性获得关于模态幅值系数方程组，进而获得声压、质点振速表达式。将声压、质点振速代入式(8)、(9)、(11)、(12)即可求得子域1、3的传递矩阵。

子域2的横截面为圆形，本征函数解析表达式[10]为

Ψi(x,y)=J0(2αir/d)

(27)

本征值αi取值见表1。将式(27)代入式(17)、(18)可得子域2管道内声压、质点振速的解析表达式。结合式(7)、(10)求得各阶模态幅值系数，代入式(8)、(9)、(11)、(12)即可求得子域2的传递矩阵。

表1　本征值αi

将所得三子域传递矩阵分别代入式(6)，利用简单矩阵运算关系即可求得消声器整体传递矩阵及消声器四极参数，进而获得消声器传递损失。

4算例及分析

为检验基于子域划分耦合方法的正确性，分别用耦合方法、三维有限元法及数值模态匹配法计算双膨胀腔消声器、双腔穿孔管消声器、有流双腔穿孔管阻性消声器及锥型连接管双膨胀腔消声器的传递损失。

4.1双极膨胀腔消声器

以图1双级膨胀腔消声器为例。消声器具体尺寸为：膨胀腔及进出口管直径为D=0.153 2 m，d=0.048 6 m，膨胀腔长度L1=L2=0.282 3 m，各插管长度为Li=Lo=0.08 m，Le1=Le2=0.04 m。分别用基于子域划分耦合法、数值模态匹配法及三维有限元法计算所得传递损失曲线见图3。由图3看出，三种方法计算结果吻合较好，从而验证耦合方法的正确性。

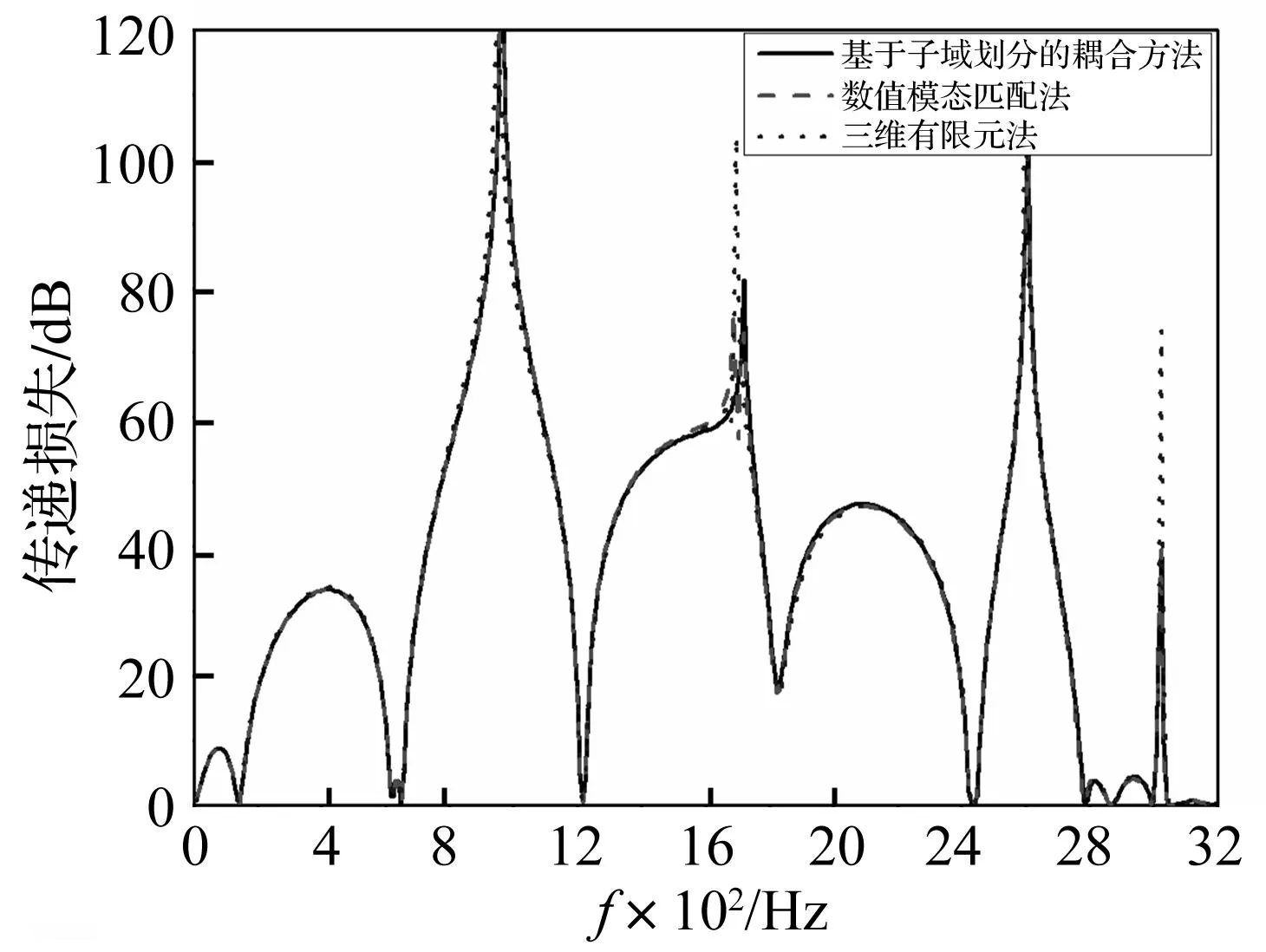
图3　双膨胀腔消声器传递损失曲线Fig.3 Transmission loss curves of silencer with double expansion chambers

文献[5]通过比较数值模态匹配法与三维有限元方法计算时间知，计算同一结构消声器时前者较后者效率更高。本文以图1双级膨胀腔为例，比较基于子域划分的耦合方法与数值模态匹配法计算速度。因耦合法求解子域的传递矩阵基于数值模态匹配法，基于子域划分的耦合法及数值模态匹配法计算消声器横向模态时间完全相同，故仅比较子域划分法计算传递矩阵、传递损失用时及数值模态匹配法计算传递损失时间。以8 Hz为步长，计算0～3 200 Hz频域内传递损失，耦合方法计算传递矩阵时间为23 s，计算传递损失时间为2 s，除计算横向模态时间，耦合方法共用时25 s。用数值模态匹配法计算传递损失时消声器连续条件较多，方程组维数较大，求解时间较长，除计算横向模态时间，数值模态匹配法用时36 s。由此可见，基于子域划分的耦合方法计算效率较数值模态匹配法略高。用数值模态匹配法计算双腔或多腔结构消声器时，由于连续及边界条件较多，程序代码较繁琐，而用基于子域划分的耦合法可直接调用子程序计算较简单。因此，计算多腔结构消声器传递损失时用子域划分法简单、快速。

4.2双腔穿孔管消声器

双腔穿孔管消声器示意图见图4。消声器膨胀腔及进出口管直径为D=0.164 4 m，d=0.049 m，膨胀腔长度L1=L2=0.257 2 m，各插管长度为Li=Lo=0.08 m，Le1=Le2=0.04 m。穿孔管孔径dh=0.002 49 m，壁厚tw=0.000 9 m，穿孔率φ=8.4%。穿孔管阻性消声器内填充吸声材料为长纤维玻璃丝绵，密度100 g/l。

图4　双腔穿孔管消声器结构示意图Fig.4 Sketch of double-chamber perforated tube silencer

通过研究消声器穿孔管内无均匀流即M=0计算消声器传递损失，所用穿孔特性声阻抗率、吸声材料特性声阻抗及特性波数表达式如下。

对穿孔管抗性消声器，穿孔特性声阻抗率表达式为

ζp=[R+jk0(tw+αdh)]/φ

(28)

式中：k0为空气中波数；R为单孔特性声阻；α为单孔声学厚度修正系数，分别表示[11]为

(29)

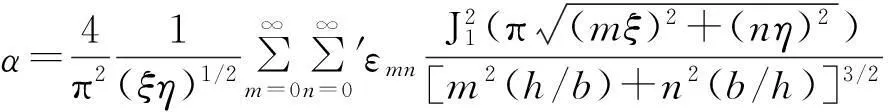
式中：ρ0为空气密度；μ为动力黏度系数；ξ=dh/b；η=dh/h；b,h为相邻两孔在两个方向的距离；上角撇号表示(0, 0) 阶模态不包括在内，m≠0且n≠0时εmn=1，其它εmn=1/2，J1为第一类一阶贝塞尔函数。

穿孔管阻性消声器的穿孔特性声阻抗率表达式修改为

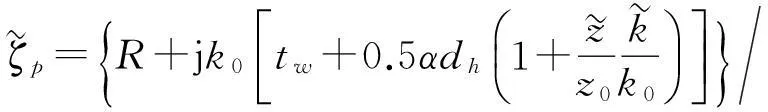
(31)

密度为100 g/l及200 g/l时长纤维玻璃丝绵特性声阻抗及特性波数表达式[12]为

(32)

(33)

式中：z0为空气中声阻抗。材料填充密度为100 g/l时a1=33.2，b1=0.752 3，a2=28.32，b2=0.651 2，a3=39.20，b3=0.684 1，a4=38.39，b4=0.628 5；材料填充密度为200 g/l时a1=25.69，b1=0.552 3，a2=71.97，b2=0.707 2，a3=56.03，b3=0.630 4，a4=62.05，b4=0.598 0。

双腔穿孔管抗性消声器及双腔穿孔管阻性消声器传递损失曲线见图5、图6。由两图看出，基于子域划分的耦合方法与有限元方法计算结果吻合较好，从而验证耦合方法计算双腔穿孔管消声器声学特性的正确性。

图5　双腔穿孔管抗性消声器传递损失曲线Fig.5 Transmission loss curves of double-chamber perforated tube reactive silencer

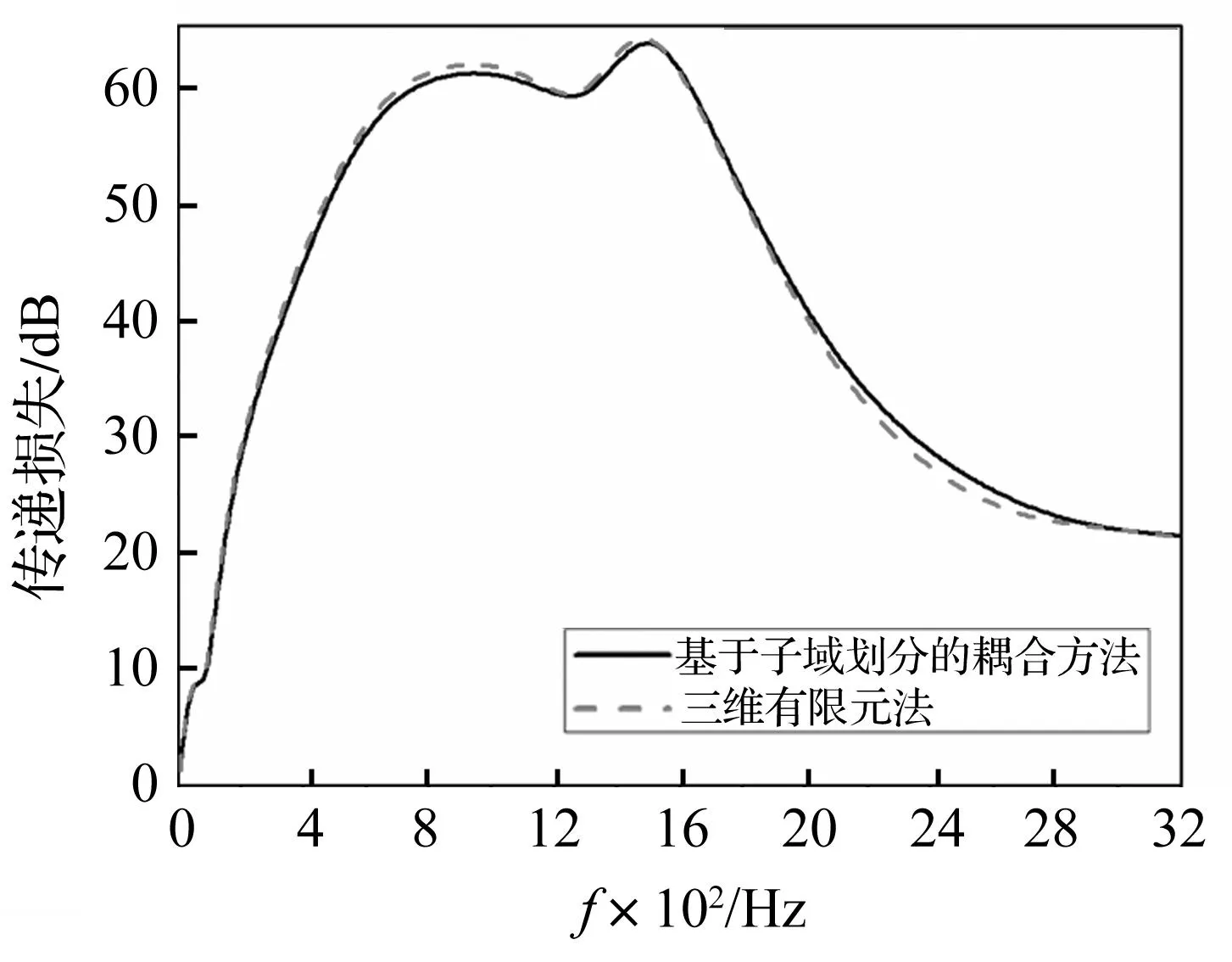
图6　双腔穿孔管阻性消声器传递损失曲线Fig.6 Transmission loss curves of double-chamber perforated tube dissipative silencer

4.3有流双腔穿孔管阻性消声器

有流双腔穿孔管阻性消声器(图4)由两个圆形横截面有流穿孔管阻性消声器连接而成。消声器具体尺寸为：膨胀腔、进出口管直径D=0.164 4 m，d=0.049 m，膨胀腔长度L1=L2=0.203 2 m，各插管长度Lin=Lout=0.08 m，Le1=Le2=0.04 m。穿孔管孔径dh=0.002 49 m，壁厚tw=0.000 9 m，穿孔率φ=25%。消声器内填充吸声材料为长纤维玻璃丝绵，密度200 g/l，其特性参数见式(32)、(33)，穿孔管内马赫数取M=0.1。

计算传递损失时用掠过流作用的穿孔声阻抗表达式[13]，即

(34)

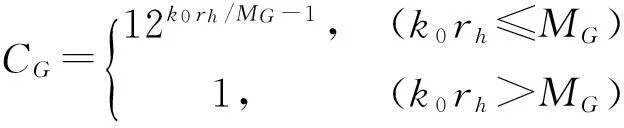
由于现有声学商业软件无法计算有流穿孔管消声器传递损失，为验证基于子域划分的耦合方法计算有流双腔消声器声学特性的适用性，用数值模态匹配法计算所得传递损失结果见图7。并与耦合方法计算结果进行比较。由图7看出，传递损失曲线吻合良好，亦验证耦合方法计算该类结构消声器声学性能的适用性。有流双腔穿孔管阻性消声器在整个频率范围内消声量较高。

图7　有流双腔穿孔管阻性消声器传递损失曲线Fig.7 Transmission loss curves of double-chamber perforated tube dissipative silencer with mean flow

4.4锥型连接管双膨胀腔消声器

以上三种结构消声器组成单元均较规则，每个声学单元中消声器横截面沿轴向均匀一致，用数值模态匹配法仍可求解传递损失，但所用程序相对繁琐。为进一步表明基于子域划分的耦合方法较数值模态匹配法的优越性，研究双腔消声器结构，见图8。该结构由渐缩锥型管道连接两膨胀腔消声器。需说明的是图8中消声器结构尺寸只为计算验证，无实际应用价值。现取消声器尺寸为：两膨胀腔消声器长度为L1=L2=0.282 3 m，膨胀腔直径相同D=0.153 2 m，进出口管直径d1=d2=0.097 2 m，d3=d4=0.048 6 m，进出口管插入膨胀腔长度L1i=L2o=0.08 m，L1o=L2i=0.04 m。中间锥型连接管长度Le=0.048 6 m，锥角θ通过锥型连接管顶面半径与底面半径计算得tanθ=0.5。

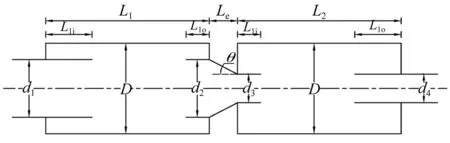
图8　锥型连接管双腔消声器结构示意图Fig.8 Sketch of double-chamber silencer with tapered connected tube

用本文方法计算该消声器传递损失时，将两膨胀腔和锥型连接管各视为一子域单元。锥型结构非常用规则声学单元，用解析方法求解该结构单元传递矩阵较复杂，此处用已有公式计算传递矩阵，由于用数值模态匹配法计算膨胀腔消声器传递矩阵时已考虑进出口管长度修正，故计算锥型管道传递矩阵时只需用实际长度即可。锥型收缩管传递矩阵系数表达式[14]为

(35)

(36)

(37)

(38)

用所提基于子域划分的耦合方法与三维有限元法计算所得消声器结构传递损失结果见图9。由图9看出，在所需频率范围内两种方法计算结果吻合良好，从而验证耦合处理方法计算横截面渐变结构消声器声学特性的适用性及精确性，亦突显出本文方法的优越性。

5结论

基于将复杂结构消声器按照结构特点划分为若干子域，用合适方法求解出每个子域的传递矩阵，通过矩阵运算求得消声器整体传递矩阵思想提出子域划分的耦合方法，并用于求解双腔结构消声器传递损失，结论如下：

(1)用耦合方法、数值模态匹配法及三维有限元法计算双膨胀腔消声器、双腔穿孔管消声器、有流双腔穿孔管阻性消声器及锥型连接管双膨胀腔消声器传递损失，其结果在研究频率范围内吻合较好，表明耦合方法的正确性。

(2)对耦合方法、数值模态匹配法计算时间比较表明，基于子域划分的耦合方法计算效率高于数值模态匹配法。而与数值模态匹配法相比可计算含渐变截面结构的消声器声学性能，且恒定截面多腔结构消声器声学特性计算程序更简单。

参 考 文 献

[1] Kirby R. Transmission loss predictions for dissipative silencers of arbitrary cross section in the presence of mean flow[J]. Journal of the Acoustical Society of America,2003,114 (1): 200-209.

[2] Albelda J, Denia F D, Torres M I,et al. A transversal substructuring mode matching method applied to the acoustic analysis of dissipative silencers[J]. Journal of Sound and Vibration,2007, 303: 614-631.

[3] Albelda J, Denia F D, Fuenmayor F J,et al. A transversal substructuring modal method for the acoustic analysis of dissipative mufflers with mean flow[C]//Acoustics’08 Paris, 2008.

[4] Kirby R. A comparison between analytical and numerical methods for modeling automotive dissipative silencer with mean flow[J].Journal of Sound and Vibration,2009, 325: 565-582.

[5] Fang Z, Ji Z L. Acoustic attenuation analysis of expansion chambers with extended inlet/outlet [J]. Noise Control Engineering Journal, 2013, 61(2):240-249.

[6] Fang Z, Ji Z L. Numerical mode matching approach for acoustic attenuation predictions of double-chamber perforated tube dissipative silencers with mean flow [J]. Journal of Computational Acoustics,2014,22(2): 1450004-1-1450004-15.

[7] 方智,季振林.穿孔管阻性消声器横向模态和声学特性计算与分析[J]. 振动与冲击, 2014, 33 (7):138-146.

FANG Zhi, JI Zhen-lin. Transversal modes and acoustic attenuation performance of a perforated tube dissipative silencer[J]. Journal of Vibration and Shock, 2014, 33(7): 138-146.

[8] 张盛,方杰,张洪武,等.基于多重多级动力子结构的Lanczos算法[J].振动与冲击,2012,31(6): 23-26.

ZHANG Sheng,FANG Jie,ZHANG Hong-wu,et al. Lanczos algorithm based on multi-level dynamic substructures[J]. Journal of Vibration and Shock, 2012, 31(6): 23-26.

[9] 周储伟,潘清. 模拟裂纹扩展的一种有限元局部动态子划分方法[J].计算力学学报,2012, 29(4): 499-504.

ZHOU Chu-wei,PAN Qing. A dynamic sub-partition strategy of finite element for simulation of crack propagation[J].Chinese Journal of Computational Mechanics, 2012, 29(4): 499-504.

[10] Munjal M L. Acoustics of ducts and mufflers[M]. New York:Wiley-Interscience, 1987.

[11] Ingard U. On the theory and design of acoustic resonators [J]. Journal of the Acoustical Society of America,1953, 25: 1037-1061.

[12] 徐贝贝,季振林. 穿孔管阻性消声器声学特性的有限元分析[J].振动与冲击,2010, 29(3): 58-62.

XU Bei-bei, JI Zhen-lin. Finite element analysis of acoustic attenuation performance of perforated tube dissipative silencers[J].Journal of Vibration and Shock, 2010, 29(3): 58-62.

[13] 康钟绪. 消声器及穿孔元件声学特性分析[D]. 哈尔滨:哈尔滨工程大学,2009.

[14] Easwavan V, Munjal M L. Plane wave analysis of conical and exponential pipes with incompressible mean flow [J]. Journal of Sound and Vibration, 1992, 152(1): 73-93.

Coupled subdomains method for the acoustic attenuation performance analysis of double-chamber silencers

FANGZhi1,JIZhen-lin2,LIUCheng-yang3

(1. School of Naval Architecture and Ocean Engineering, Huazhong University of Science and Technology, Wuhan 430074,China;2. College of Power and Energy Engineering, Harbin Engineering University, Harbin 150001,China;3. China Ship Development and Design Center, Wuhan 430064,China)

Abstract:For the acoustic attenuation performance analysis of double-chamber silencers, a coupled subdomains method was proposed. The silencer was divided into several substructures according to its geometry characteristics and material characteristics. The 3D analytical method or numerical mode matching method was applied to calculate the transfer matrixes of the substructures with regular cross-section, and the 3D numerical method was used for the substructures with irregular cross-section. The integer transfer matrix of the silencer was calculated in the light of the continuity conditions at the interfaces of substructures, and the transmission loss was then derived. The transmission loss of several typical double-chamber silencers were calculated by using the proposed method, the finite element method and the numerical mode matching method respectively. The results show that the coupled submains method is applicable for the double-chamber silencers, and more efficient than the numerical mode matching method.

Key words:silencer; acoustic attenuation characteristics; coupling method; numerical mode matching method

中图分类号:TK421

文献标志码：A

DOI:10.13465/j.cnki.jvs.2016.06.005

收稿日期：2015-01-16修改稿收到日期：2015-03-23

基金项目：国家自然科学基金资助项目(11504119)；华中科技大学自主创新基金项目(2015QN017)

第一作者 方智 女，博士,讲师,1987年生

E-mail:zihuiying@163.com