流量不均鱼骨状多分支水平井不稳定压力分析

黄　瑶，程时清，何佑伟，于海洋

中国石油大学(北京)石油工程教育部重点实验室，北京 102249



流量不均鱼骨状多分支水平井不稳定压力分析

黄瑶，程时清，何佑伟，于海洋

中国石油大学(北京)石油工程教育部重点实验室，北京 102249

摘要：为研究分支井和主井筒流量密度分布不均及各生产段表皮分布不均对鱼骨状多分支水平井井底压力(bottom hole pressure, BHP)的影响，通过将分支井段和水平主井筒段考虑成线源，运用格林函数并结合Newman乘积方法，建立了鱼骨状多分支水平井非均匀流量的试井解释模型，利用数值反演算法计算BHP，绘制出典型试井曲线并进行敏感性因素分析．结果表明，该模型出现了新的渗流特征段，其特征段在压力导数曲线上呈现出斜率大于0.5的直线段，将其命名为分支干扰线性流动段．鱼骨状多分支水平井分支井段及主井筒段流量不均时，BHP响应与各分支井段及主井筒段的流量以及表皮分布密切相关，同时也受到分支的长度、角度、地层各向异性、井筒在地层中高度和分支在主井筒上位置等因素的影响．该模型对鱼骨状水平井的产油井段诊断与解释、储层伤害判断以及增产措施制定有指导意义．

关键词：油气田开发；流量密度分布不均；表皮分布不均；不稳定压力分析；鱼骨状多分支水平井；分支干扰线性流；格林函数；Newman乘积

多分支井技术已被广泛用于油气藏开发以达到增产和提高采收率的目的．由于多分支井在低渗透油田和海上油田乃至致密油气田开采上都具有广阔的应用前景[1-2]，国内外针对水平井及多分支水平井的渗流特征进行了大量的研究．

在数值模拟方面，学者们通过建立数学模型求解等方法，从不同侧面对多分支井的压力响应进行了分析．其中，点源函数自1973年被Gringarten等[3]引入油藏渗流问题之后，在水平井和分支井的渗流问题研究中得到了广泛的应用．Karakas等[4]最先通过运用数值模拟技术对双分支水平井和多分支水平井的压力响应进行了预测，并对双分支水平井进行了实例分析．Raghavan等[5]提出了数学模型来研究多分支井的压力响应并给出了半解析解，且在此基础上绘制了典型试井曲线图版．Ozkan等[6]在考虑分支井长度、角度、两分支垂直距离和纵向距离的基础上，针对双分支水平井提出了数学模型并给出了解析解，其研究结果表明，当两分支之间距离足够长时，每个分支将出现独立于另一个分支之外的拟径向流，这个流态被命名为中期拟径向流．在此之后，Larsen[7]通过将每个分支分成小段并将每分支小段近似看成一个裂缝得到了多层合采多分支井的半解析解并绘制了相应的典型试井曲线．Ouyang等[8]在考虑井储、井壁摩擦损耗以及动能损失的基础上运用点源函数建立了一个半解析的数学模型来研究任意数目任意形状位置的多分支井．Yildiz[9]提出了三维的解析模型去研究流入多分支井的瞬态流动，并在此基础上讨论了地层各向异性以及分支附近地层不同伤害程度对压力响应的影响．杨雷等[10]应用连续点源解建立了大斜度井和分支井的压力分布模型，考虑了大斜度井射开段长度、上下位置、倾斜角和渗透率各向异性的影响．段永刚等[11]随后利用单支水平井的压力分布叠加得到了多分支井的压力分布，采用井筒流动与油藏流入的相互耦合，得到了几种多分支井压力不稳定曲线并划分了不同多分支井的渗流特征段．黄世军等[12]在考虑多分支井各分支在主井眼井底的相互干扰以及采油举升的基础上，提出了整体压力系统分析模型．孔祥言等[13]利用坐标旋转推导出无限大平面的任意方向线段源函数，然后通过平面线源函数叠加对平面多分支井进行了压力分析并得到了典型试井曲线．张利军等[14]进一步通过叠加线段源函数和Laplace反演得到了考虑井储和表皮的不同形状及不同边界条件下复杂结构井井底压力(bottom hole pressure, BHP)的半解析解，并讨论了分支井各参数对试井曲线的影响．Medeiros等[15]讨论研究了多层以及复合储层中的水平井和多分支水平井的压力响应，并得出了半解析解.

近年来，国内外针对水平井，压裂水平井及多分支水平井的不稳定压力分析均从不同的角度进行了研究[16-21]. 然而，上述研究方法均假设流体以均匀的流量流入各分支井以及主井筒，而在实际的生产过程中，由于储层的非均质性和储层污染以及井眼堵塞等原因，流体流入分支井和主井筒的流量会出现不均匀分布的情况．本研究针对流量分布不均以及表皮分布不均匀问题，建立了新的鱼骨状多分支水平井试井解释模型，并提出了结合实际试井资料判断鱼骨状多分支井有效产油段的新方法．

1鱼骨状多分支水平井不均流量试井解释模型

1.1物理模型

考虑顶底封闭、水平方向无限大的油藏中有N段分支井的鱼骨状多分支水平井，水平井筒与分支井筒段均垂直于z轴方向．其中，第i段分支井与水平井筒交点为(ai，0，zw)处，长度为2Li； 与主井筒夹角为αi； 流量为qi； 表皮系数为Si． 此外，主井筒长度为2L； 流量为q0； 表皮系数为S0， 中心坐标为(xw0，yw0， zw)． 油藏均质且渗透率各向异性，油藏中任一点的水平渗透率为Kx=Ky=Kh， 垂直渗透率为Kz=Kv． 流体同时流向分支井筒段和水平井筒段．其余参数为：油藏孔隙度为φ； 油藏厚度为h； 综合压缩系数为Ct； 黏度为μ；单相流体，忽略毛管力和重力影响．物理模型见图1.

图1　鱼骨状多分支水平井物理模型Fig.1　Physical model of fishbone multi-lateral horizontal well

1.2数学模型及解

对于鱼骨状多分支水平井水平方向渗透率Kh与垂直方向渗透率Kv不相等的三维渗流问题，若引入

(1)

则鱼骨状多分支水平井三维渗流偏微分方程可化为如下标准形式

(2)

其中，

(3)

水平主井筒段和分支井段均垂直于z轴方向，均可视为上下边界封闭无限大空间线段源，鱼骨状多分支水平分支井的地层压力可由线段源叠加得到

p(x,y,z,t)= pi-1ϕCt∑Ni=1qi2Li∫t0GxGyzdτ-

(4)

其中，

(5)

(6)

(7)

(8)

其中，

(9)

定义如下无量纲

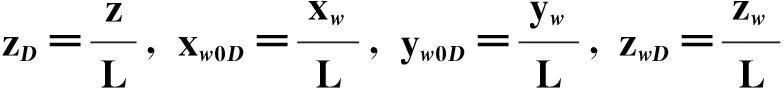
(10)

则可得到无量纲鱼骨状多分支水平无因次井底地层压力分布

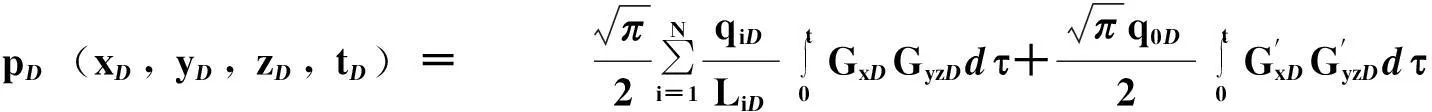
pD(xD,yD,zD,tD)= π2∑Ni=1qiDLiD∫t0GxDGyzDdτ+πq0D2∫t0G'xDG'yzDdτ

(11)

其中，

(12)

(13)

(14)

(15)

考虑各个分支井生产段不同的表皮Si以及主井筒段表皮S0后，鱼骨状多分支水平井地层无因次地层压力分布为

pSD(xD,yD,zD,tD)=

(16)

式(16)是未考虑井筒储集效应的水平井无因次井底压力解.

考虑井储效应后井底压降为

(17)

对式(17)进行拉普拉斯变换，得到拉氏空间中鱼骨状多分支水平井考虑表皮和井储存的压降为

(18)

2典型试井曲线及渗流流态分析

在式(16)中取计算点xD=0， yD=0， zD=zwD． 对式(18)进行Stehfest数值反演[16]可算出鱼骨状多分支水平井在实空间的井底压力pwD， 从而绘制出典型试井曲线，见图2．

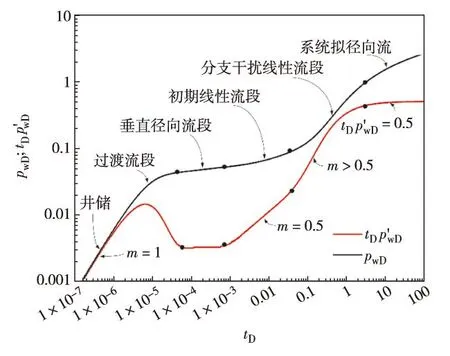
图2　鱼骨状多分支水平井典型试井曲线Fig.2　Typical curves of fishbone multi-lateral horizontal well

从图2可以看出，鱼骨状多分支水平井的流动阶段可以分为6个阶段：

1)第1阶段为井筒储集段．流动主要受井筒储集效应的影响，压力和压力导数曲线都呈现斜率为1的重合直线段．

2)第2阶段为过渡流动段．压力导数曲线呈现明显驼峰段，该流动段主要受表皮系数影响．

3)第3阶段为垂直径向流动段．井储和过渡流动段结束后，储层中的主要流动是在水平井段和各分支井段垂直截面上的径向流动，在压力导数曲线上呈现水平段．

4)第4阶段为初期线性流动段．在压力波及顶底边界之后，流动进入线性流动阶段，水平井和各分支井的垂直截面上，流动是水平的，在压力导数曲线上呈现斜率为0.5的直线段．

5)第5阶段为分支干扰线性流动段．流体水平流入各分支井段和主水平井筒段，各线性流动互相干扰，从而在压力导数曲线呈现斜率大于0.5的直线段．

6)第6阶段为系统拟径向流动段．此时，相对无限大地层，整个分支井系统可以看做一个“点”，全井系统达到径向流动阶段，在压力导数曲线上呈现值为0.5的水平段．

3敏感性因素分析

下面讨论单一分支井段流量、主井筒段分支流量、部分分支井段零流量、各分支井段及主井筒段表皮非均匀分布、分支数目、分支井段与主井筒段夹角、地层纵向横向渗透率比、井筒在地层中的垂向高度、分支位置、分支井产油段长度对试井曲线的影响．

3.1单一分支井段流量的影响

图3以鱼骨状6分支水平井的第1分支井段为例，展示了单一分支井段流量对鱼骨状多分支水平井试井曲线的影响，其中q1D=0表示第1段无流量的情况，而q1D=0.125表示所有分支及主井筒均匀流量的情况．如图3所示，随着q1D值的增大，过渡流动段、垂直径向流动段以及线性流动段的压力和压力导数值降低，而表征分支干扰线性流的压力导数直线斜率变大．

图3　单一分支井段流量对鱼骨状多分支水平井试井曲线的影响Fig.3　Comparison of BHP and BHP derivative curves under different values of q1D

图4　主井筒段流量对鱼骨状多分支水平井试井曲线的影响Fig.4　Comparison of BHP and BHP derivative curves under different values of q0D

3.2主井筒段流量的影响

主井筒段长度一定前提下，主井筒段流量对顶底封闭的鱼骨状多分支水平井试井曲线的影响如图4． q0D值主要影响过渡流动段、线性流动段和分支干扰线性流动段，随着q0D值的增大过渡流动段驼峰升高，垂直径向流动段持续时间缩短，且表征分支干扰线性流动段的压力导数直线斜率变小趋近于0.5．在图4中， q0D= 0.25表示所有分支及主井筒均匀流量的情况，从图4中可以看出，当q0D=0.35， 也就是主井筒段流量贡献比例很大时，分支干扰线性流动段趋于消失，压力导数曲线形态近似于水平井．

图5　部分分支井无流量对鱼骨状多分支水平井试井曲线的影响Fig.5　Comparison of BHP and BHP derivative curves under different values of qiD

3.3部分分支井段零流量的影响

图5以鱼骨状6分支水平井为例，展示了部分分支井段零流量对鱼骨状多分支水平井试井曲线的影响．在图5中可以看出，当qiD=0.125， 即所有分支井段及主井筒均匀流量情况下压力最低；随着零流量分支井段数目的增加，过渡流动段驼峰升高，垂直径向流动段持续时间缩短，分支干扰线性流动段出现时间推迟．当所有分支井段均零流量时，相当于单水平井， 此时分支干扰线性流完全消失．

3.4各分支井段及主井筒段表皮不均匀分布的影响

由式(16)可以看出，表皮项与各生产段的流量与长度有关，当qiD、LiD以及q0D值不变时，分支井段表皮和主井筒表皮之和一定，各段表皮分布不同对井底压力响应没有影响．而当分支井段流量qi呈现两端流量大中间流量小的分布形式时，虽然分支井段的表皮之和一定，但是由于各分支井段流量分布不均，表皮的非均匀分布会对井底压力响应产生影响，如图6所示．可以看出，当两端分支井段表皮系数较大时，造成的压降损失最大，而中间分支井段表皮系数较大时，造成的压降损失最小．

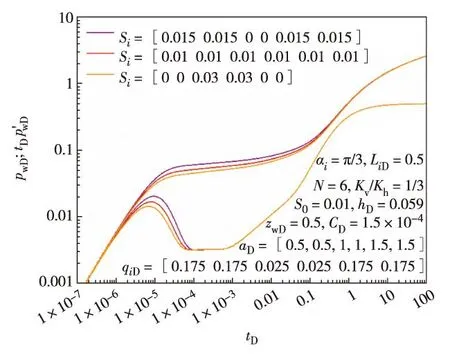
图6　非均匀分布表皮对鱼骨状多分支水平井试井曲线的影响Fig.6　Comparison of BHP and BHP derivative curves under different values of Si

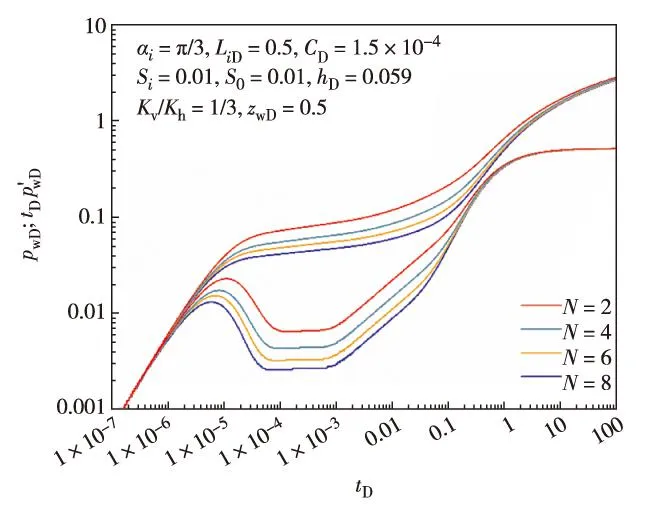
图7　分支井段数目对鱼骨状多分支水平井试井曲线的影响Fig.7　Comparison of BHP and BHP derivative curves under different values of N

3.5分支井段数目的影响

分支井段数目N对鱼骨状多分支水平井试井曲线的影响如图7． N值影响双对数曲线的过渡段、早期径向流动段、早期线性流动段以及分支干扰线性流动段．压力和压力导数随着分支数目的增多而降低．随着N值的增大，过渡流动段驼峰降低，分支干扰线性流动段出现提前且持续时间增加，同时表征该流动段的压力导数曲线斜率增大．这说明，均匀出油情况下，分支井段数目越多，各分支段以及主井筒段之间的流动干扰越明显．

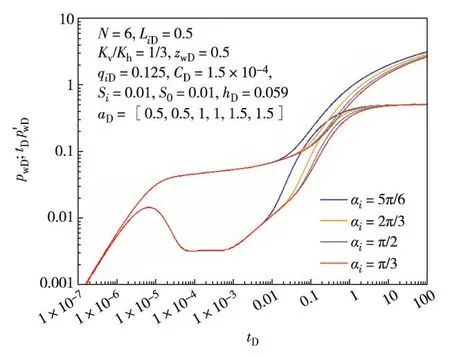
图8　支与主井筒夹角对鱼骨状多分支水平井试井曲线的影响Fig.8　Comparison of BHP and BHP derivative curves under different values of αi

3.6分支井段与主井筒段夹角的影响

图8以鱼骨状6分支水平井为例，展示了分支井段与主井筒段的夹角αi对鱼骨状多分支水平井试井曲线的影响． αi值只影响线性流动段和分支干扰线性流动段，当αi值增大，线性流动段的时间缩短，分支干扰线性流动段时间提前且此流动段压力升高，但表征该流动段的压力导数曲线斜率不变．说明分支井段与主井筒段夹角越大，分支间出现干扰的时间越提前．

3.7地层纵向横向渗透率比的影响

地层纵向横向渗透率比Kv/Kh对顶底封闭的鱼骨状多分支水平井试井曲线的影响如图9． Kv/Kh值主要影响过渡流动段和早期径向流动段，随着Kv/Kh值的增大驼峰降低，且垂直径向流动段持续时间缩短，早期线性流动持续时间增大，而分支干扰线性流动段和系统拟径向流动段不受影响．这表明地层渗透率各向异性越大，压力波到达顶底封闭边界所需时间越长．

图9　地层纵向横向渗透率比对鱼骨状多分支水平井试井曲线的影响Fig.9　Comparison of BHP and BHP derivative curves under different values of Kv/Kh

3.8地层中垂向高度的影响

图10以鱼骨状6分支水平井为例，展示了地层中垂向高度zwD对鱼骨状多分支水平井试井曲线的影响．由图10可以看出， zwD值主要影响早期径向流动段，表现为zwD值越大，早期垂直径向流动段结束越早．这是因为当zwD值越大时，井筒离顶端边界越近，压力波传到顶端所需时间越短．此外，因为对称性，在zwD小于0.5的时候， zwD越小，早期垂直径向流动段结束越早．

图10　多分支水平井在地层中垂向高度对鱼骨状多分支水平井试井曲线的影响Fig.10　Comparison of BHP and BHP derivative curves under different values of zwD

3.9分支井段长度的影响

主井筒段长度一定前提下，分支井段长度对顶底封闭的鱼骨状多分支水平井试井曲线的影响如图11． LiD值主要影响过渡流动段和分支干扰线性流动段；随着LiD值的增大过渡流动段驼峰降低，且表征分支干扰线性流动段的压力导数直线斜率变小，而垂直径向流动段和早期线性流动段基本不受影响．

图11　分支井长度对鱼骨状多分支水平井试井曲线的影响Fig.11　Comparison of BHP and BHP derivative curves under different values of LiD

3.10分支井段在主井筒上位置的影响

图12以鱼骨状6分支水平井为例，展示了各分支井在主井筒上位置对鱼骨状多分支水平井试井曲线的影响．由图12可以看出，分支井段在主井筒段上位置主要影响分支干扰线性流动段，表现为分支井段在主井筒段上分布越远离主井眼，分支干扰线性流动段出现时间越晚．

图12　分支井段在主井筒段上位置对鱼骨状多分支水平井试井曲线的影响Fig.12　Comparison of BHP and BHP derivative curves under different values of aD

4本模型实际工程应用方法

基于本文建立的新模型，编制了用于拟合鱼骨状多分支井井底压力和压力导数的自动拟合程序．通过给出一组初始地层参数，运用拟合程序进行自动拟合之后得出最优解．同时为了解决试井解释中普遍存在的多解性问题，在进行优化拟合的同时，还需要结合测试井的测井完井资料，以及其他地质资料确定地层参数的合理范围，以便得到更加准确有效的拟合解释参数．

5结论

1)建立了考虑分支井数目、角度、位置以及各分支井段和主井筒段流量不均的鱼骨状分支井试井解新模型．将分支井段和主井筒段视为线段源，通过线段源的叠加和Newman乘积原理推导出鱼骨状水平井的格林函数，再通过卷积的拉式变换，给出了拉氏空间下考虑井储和各分支段及主井筒段不同表皮的井底压力严格表达式，通过数值反演计算得出鱼骨状水平井的井底压力解，并绘制出了典型试井曲线．

2)新模型出现了新的渗流特征段，将其命名为分支干扰线性流动段，该流动段在压力导数曲线上呈现为斜率大于0.5的直线段．随着第1分支井段流量增大，主井筒段流量减少，无流量的分支井段数目减少，分支井段数目增多，分支段与主井筒段角度增大，分支井段长度变短，分支井段在主井筒段上分布越靠近主井眼，分支干扰线性流动段出现时间提前．

3)鱼骨状水平井主井筒的长度相同时，第1分支井段流量越大，主井筒段流量越小，无流量的分支井段数目越少时，分支井段数目越多，分支段与主井筒段角度越小，分支井段长度越长，分支井段在主井筒段上分布越远离主井眼，井底无量纲压力越低．

4)当各分支井段长度与流量相同时，若总的表皮之和一定，则各段非均匀分布的表皮造成的压力响应相同；当各分支井段段长度与流量不相同时，即使各段总的表皮之和一定，各段非均匀分布表皮在井底产生的压力响应却不相同．其中，当分支井段流量呈现U型分布时，两端分支井段表皮较大的情况下压降损失最大．

5)本模型考虑了分支井段及主井筒段流量不均情况，因而可以有效诊断鱼骨状多分支井分支有效产油部位，为储层伤害判断和增产措施制定提供依据．

引文：黄瑶，程时清，何佑伟，等．流量不均鱼骨状多分支水平井不稳定压力分析[J]. 深圳大学学报理工版，2016，33(2)：202-210.

参考文献/ References：

[1] Denney D. Multilateral well in low-productivity zones[J]. Journal of Petroleum Technology, 1998, 50(7): 42-44.

[2] Fipke S R, Celli A O. The use of multilateral well designs for improved recovery in heavy-oil reservoirs[C]// IADC/SPE Drilling Conference. Orlando, USA：[s. n.], 2008: 112638.

[3] Gringarten A C, Ramey H J. The use of source and Green’s functions in solving unsteady-flow problems in reservoirs[J]. Society of Petroleum Engineers Journal, 1973, 13(5): 285-296.

[4] Karakas M, Yokoyama Y, Arima E. Well test analysis of a well with multiple horizontal drainholes[C]// Middle East Oil Show. Manama, Bahrain：[s. n.], 1991:21424.

[5] Raghavan R, Ambastha A. An assessment of the productivity of multilateral completions[J]. Journal of Canadian Petroleum Technology, 1998, 37(10): 58-67.

[6] Ozkan E, Yildiz T, Kuchuk F. Transient pressure behavior of dual-lateral wells[J]. SPE Journal, 1998, 3(2): 181-190.

[7] Larsen L. Pressure-transient behavior of multibranched wells in layered reservoirs[J]. SPE Reservoir Evaluation & Engineering, 2000, 3(1): 68-73.

[8] Ouyang L B, Aziz K, Ouyang L B, et al. A simplified approach to couple wellbore flow and reservoir inflow for arbitrary well configurations[J]. Producing Well, 1998:79-91.

[9] Yildiz T. Multilateral pressure-transient response[J]. SPE Journal, 2003, 8(1): 5-12.

[10] 杨雷，黄诚，段永刚，等. 大斜度井、分支井的不稳定压力动态分析[J]. 西南石油学院学报, 2002, 24(2): 25-27.

Yang Lei, Huang Cheng, Duan Yonggang, et al. Pressure-transient analysis of highly devative wells and multilateral wells[J]. Journal of Southwest Petrolum Institude, 2002, 24(2): 25-27.(in Chinese)

[11] 段永刚，陈伟，黄天虎，等. 多分支井渗流和不稳定压力特征分析[C]//第九届全国渗流力学学术讨论会论文汇编, 西安中国：[s. n.], 2007:136-138.

Duan Yonggang, Chen Wei, Huang Tianhu, et al. Pressure-transient analysis of multilateral wells[C]// The 9th National Conference on Porous Flow. Xi’an, China:[s. n.]. 2007:136-138.(in Chinese)

[12] 黄世军, 程林松, 李秀生, 等. 多分支水平井压力系统分析模型[J]. 石油学报, 2003, 24(6):81-86.

Huang Shijun, Chen Linsong, Li Xiusheng, et al. Pressure system analysis for multi-lateral horizontal well[J]. Acta Petrolei Sinica, 2003, 24(6): 81-86.(in Chinese)

[13] 孔祥言，徐献芝，卢德唐. 分支水平井的样板曲线和试井分析[J]. 石油学报, 1997. 18(3): 98-104.

Kong Xiangyan, Xu Xianzhi, Lu Detang. A type-curve of horizontal well with multi-branched wells[J]. Acta Petrolei Sinica, 1997, 18(3): 98-104.(in Chinese)

[14] 张利军，程时清. 分支水平井试井压力分析[J]. 石油钻探技术, 2009, 37(1): 23-28.

Zhang Lijun, Cheng Shiqing. Well test pressure analysis on multilateral horizontal wells[J]. Petroleum Drilling Techniques, 2009, 37(1): 23-28.(in Chinese)

[15] Medeiros F, Ozkan E, Kazemi H, et al. A semianalytical, pressure-transient model for horizontal and multilateral wells in composite, layered, and compartmentalized reservoirs[C]// Society of Petroleum Engineers Annual Technical Conference and Exhibition. San Antonio, USA：[s.n.], 2006:102834.

[16] Lee S J, Kim T H, Lee K S. Type curves for pressure transient analysis of horizontal wells in shale gas reservoirs[C]// Society of Petroleum Engineers Middle East Oil and Gas Show and Conference. Manama, Bahrain：[s.n.], 2013:164191.

[17] Clarkson C R, Clarkson C R. Production data analysis of unconventional gas wells: review of theory and best practices[J]. International Journal of Coal Geology, 2013, 109/110(2):101-146.

[18] Chen Zhiming, Liao XinWei, Zhao Xiaoliang, et al. Performance of horizontal wells with fracture networks in shale gas formation[J]. Journal of Petroleum Science & Engineering, 2015, 133:646-664.

[19] Kim T H, Lee K S. Pressure-transient characteristics of hydraulically fractured horizontal wells in shale-gas reservoirs with natural- and rejuvenated-fracture networks[J]. Journal of Canadian Petroleum Technology, 2015, 54:245-258.

[20] Ozkan E, Brown M L, Raghavan R, et al. Comparison of fractured-horizontal-well performance in tight sand and shale reservoirs[J]. SPE Reservoir Evaluation & Engineering, 2011, 14(2):248-259.

[21] 谢斌，王俊超，黄波，等. 双重介质油藏压裂水平井非稳态压力动态分析[J]. 深圳大学学报理工版，2015，32(3):272-280.

Xie Bin, Wang Junchao, Huang Bo, et al. Unsteady pressure behavior analysis for fractured horizontal well in dual-porosity reservoir[J]．Journal of Shenzhen University Science and Engineering，2015，32(3): 272-280.(in Chinese).

[22] 廉培庆, 陈志海, 董广为,等. 水平井与非均质盒式油藏耦合模型[J]. 深圳大学学报理工版, 2015, 32(3):266-271.

Lian Peiqing，Chen Zhihai，Dong Guangwei，et al. A coupling model for horizontal well in heterogeneous box-shaped reservoir[J]．Journal of Shenzhen University Science and Engineering，2015，32(3): 266-271．(in Chinese)

[23] Stehfest H. Algorithm 368: numerical inversion of Laplace transforms[J]. Communications of the ACM, 1970, 13(1): 47-49.

【中文责编：晨兮；英文责编：天澜】

Transient pressure analysis of fishbone multi-lateral horizontal well with non-uniform flux density

Huang Yao, Cheng Shiqing†, He Youwei, and Yu Haiyang

MOE Key Laboratory of Petroleum Engineering, China University of Petroleum, Beijing 102249, P.R.China

Abstract：By using Green’s function and the Newman production method, a new well testing interpretation model is established to investigate the effect of non-uniform flux density and skin factor of laterals on transient pressure behavior of fishbone multi-lateral horizontal wells. New semi-analytical solutions of bottom hole pressure and type curves are developed based on the new model by using the Stehfest algorithm for numerical inversion, while sensitivity analysis is conducted accordingly. The proposed model discloses a new flow regime termed as the lateral interference linear flow regime, which can be characterized by appearing a straight line segment with a slope greater than 0.5 on the bottom-hole pressure derivative curve. The results of sensitivity analysis show that the bottom-hole pressure and pressure derivative are closely related to the distribution of non-uniform flux density, and skin factors of different laterals, meanwhile, are affected by factors such as the section length, orientation, reservoir anisotropy, well height in the formation, and junction locations of well laterals with the primary well sections. The proposed model can assist the interpretation of productive laterals, the estimation of formation damage, and the stimulation measure making in oil industry.

Key words：oil and gas field development; non-uniform flux density; non-uniform skin factor; transient pressure analysis; fishbone multi-lateral horizontal well; lateral interference linear flow; Green’s function; Newman product method

作者简介：黄瑶(1988—)，女，中国石油大学(北京)硕士研究生．研究方向：油气田开发．E-mail：isabelhy@163.com

基金项目：国家“十二五”科技重大专项资助项目(2011ZX05009-005-01C)

中图分类号：TE 312

文献标志码：A

doi：10.3724/SP.J.1249.2016.02202

Received：2015-09-18；Accepted：2015-12-01

Foundation：National Science and Technology Major Special Program for the 12th Five-Year Plan of China(2011ZX05009-005-01C)

† Corresponding author：Professor Cheng Shiqing．E-mail: chengsq973@163.com

Citation：Huang Yao, Cheng Shiqing, He Youwei, et al．Transient pressure analysis of fishbone multi-lateral horizontal well with non-uniform flux density[J]. Journal of Shenzhen University Science and Engineering, 2016, 33(2): 202-210.(in Chinese)

【环境与能源 / Environment and Energy】