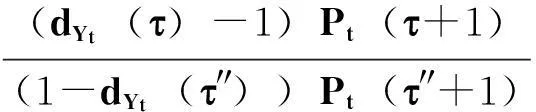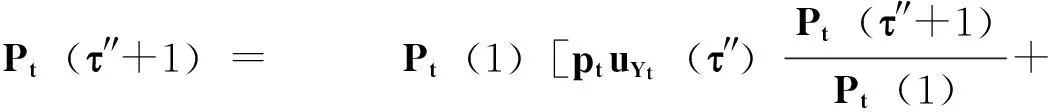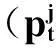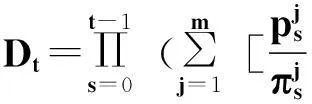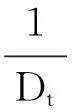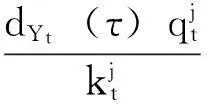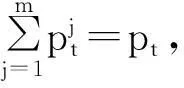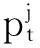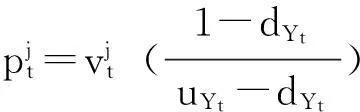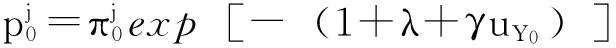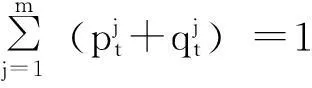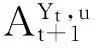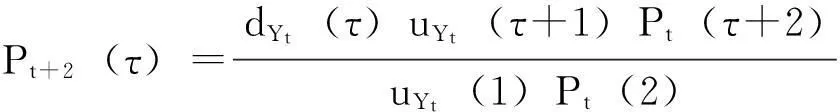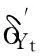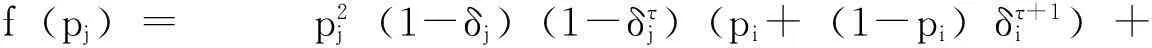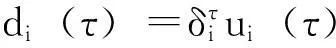最小熵鞅测度下的半马氏市道轮换利率模型

柳向东，王星蕊

暨南大学经济学院，广东广州 510632



最小熵鞅测度下的半马氏市道轮换利率模型

柳向东，王星蕊

暨南大学经济学院，广东广州 510632

摘要：讨论零息债券价格演变，基于Ho-Lee模型，应用无套利原理和鞅测度方法，建立离散时间半马氏过程控制的市道轮换下的二叉树期限结构模型．运用最小熵鞅测度处理上述模型，并在马氏和半马氏市道下给出模型在欧式债券期权定价方面的应用．

关键词：应用统计数学；Ho-Lee模型；无套利方法；二叉树模型；利率期限结构；最小熵鞅测度；债券期权定价

利率作为证券定价的核心变量之一，如何对其进行有效预测是资产定价的关键．经典的利率模型包括Ho-Lee模型、Vasicek模型、CIR模型和Hull-White模型[1-4]．大量研究发现，经济周期或货币政策的变化会导致利率在不同时期呈现不一样的变化，经济状态的改变应该引起模型参数的一个突变，市道轮换模型便成为一种很具吸引力的建模方法．Goldfeld等[5]将市道轮换回归模型用于描述非线性经济数据；Hamilton[6]在经济和计量经济学研究中推广了市道轮换时间序列模型．此后，探讨如何使用市道轮换模型模拟经济和金融数据引起人们广泛重视．市道轮换模型在金融衍生品、利率和投资组合优化中的应用，很大一部分集中于马氏轮换模型[7-11]．尽管简单的齐次马氏轮换模型受欢迎，仍存在许多缺点，主要表现在：① 由于马氏过程的无记忆性，在现实世界的数据中，马氏轮换模型并不合理[12]；② 对于轮换过程，常数轮换概率对于利率数据是不现实的[13]；③ Diebold等[14]记录表明轮换过程对经济周期应该呈现持续性的依赖，而马氏轮换模型不能体现此特征．而以上缺点都可通过半马氏轮换模型轻松处理．此外，马氏过程是半马氏过程的一个子类，半马氏轮换模型应该至少表现为马氏轮换模型，同时复杂性几乎没有增加，并且Hong 等[15]已经证明利率数据通常拒绝马氏性，然而它在半马氏轮换方向上是有意义的，这些原因都推动了使用半马氏轮换模型来替代马氏轮换过程．现有文献主要在连续时间半马氏市道轮换框架下进行研究[12,16-17]，很少关注离散时间框架下的期权定价问题．

本研究探讨离散时间半马氏市道轮换下的利率期限结构．采用金融数学的无套利理论与方法，将Ho-Lee模型推广至离散时间半马氏市道轮换的框架下，对债券和债券期权进行定价．首先回顾离散时间半马氏过程，介绍一个存在市道轮换的市场模型，讨论无套利概念及在离散时间半马氏市道轮换框架下其与鞅测度的关系，通过选取最小熵鞅测度处理市场的不完备性；然后讨论市道轮换下路径独立性的概念，给出模型和测度的一个应用，在马氏和半马氏轮换框架下定价欧式债券期权．

1半马氏市道轮换利率模型

离散时间期限结构模型主要研究直接模拟利率和模拟零息债券的演化．本文重点讨论后者．

1.1二叉树市道轮换期限结构模型的框架

考虑建立在概率空间(Ω，F，)上的1个离散时间金融市场．假设金融交易只能发生在固定的时间0，1，2，…，T*， 记T={0，1，…，T*}． 对于有限数m，定义集合E={1,2,…，m}． 假设概率空间上有一对取值于E×N的过程(Xn,Tn)，(Xn,Tn)是半马氏核Q的齐次马氏更新过程，即对所有的n,Xn,j和t， 有

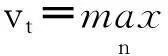
定义一个到期日为T≤T*的零息债券是在到期日T产生一单位货币的金融产品．用τ表示t时刻距离零息债券到期日的时间，即τ=T-t． 记Pt(τ)为t时刻距离到期日时间为τ的零息债券的价格．假设给定一个初始期限结构，即对所有的τ， 给定Pt(τ)的一组值．对任意的τ和状态i∈E， 假设存在两个实值ui(τ)和di(τ)， ui(τ)和di(τ)都是严格为正的，且ui(τ)>di(τ)． 记ui=(ui(1),ui(2), …, ui(T*))， di=(di(1), di(2), …, di(T*))． 引入规模为T*的一个随机过程ζt， 规定)=1-和dYt分别为Yt状态下向上和向下游走的倍数． 该过程描述了从t时刻到t+1时刻期限结构的演化，若ζt+1=uYt， 称期限结构向上移动，若ζt+1=dYt， 则称期限结构向下移动，假设在给定Ft的条件下， ζt+1与Yt+1是条件独立的，即对于任意的t≥1，记根据过程Y的结构， 有vtj=

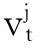
【证】记qij(t)=则Qij(t)=为半马氏核； Hi(t)=为过程在状态i逗留时间的分布函数；为时刻0从状态i出发，半马氏链在时刻t跳跃到状态j的概率；(Xk=j, Tk=t)为半马氏链在时刻t跳跃到状态j的概率；

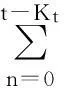
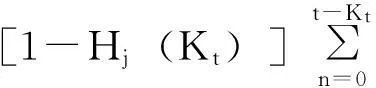
若下一个交易时刻经济状态发生跳跃，即j≠Yt， 则

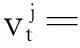
vjt=

若下一个交易时刻经济状态没有发生跳跃，即j=Yt， 则

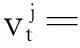
vjt=

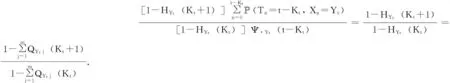
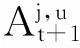
1.2Ho-Lee模型的拓展

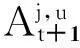
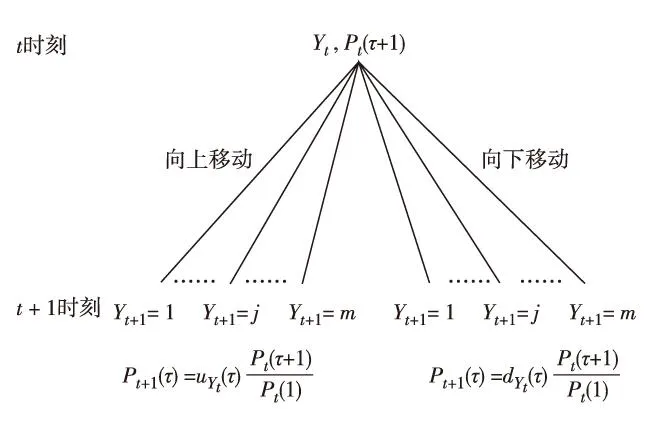
图1　半马氏市道轮换下的二叉树Fig.1　Binary tree under semi-Markov regime switching

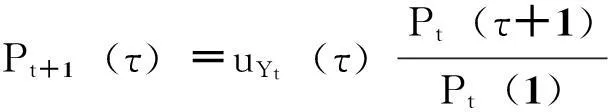
1.3无套利框架下的利率结构

套利策略是指在没有风险、没有初始投资的情况下得到确定利润的策略．市场上没有套利策略称为无套利条件．下面证明无套利意味着模型参数满足一些条件．

引理1无套利表明，对于每个τ和i∈E， ui(τ)>1>di(τ)．

定理2无套利意味着满足下列条件的过程pt存在：

对于每个t， 0

【证】 考虑1个单期模型．假设给定零息债券价格Pt(·)的结构，构建一个投资组合：包含1个到期日为T+1的零息债券(距离到期日的时间为τ+1)和H个到期日为T″+1的零息债券(距离到期日的时间为τ″+1)．

在时刻t， 投资组合的价值为W(t)=Pt(τ+1)+HPt(τ″+1)．

在时刻t+1， 根据本研究建立的模型，投资组合能且只能取2个值.

现选取一个H使其满足无论哪个事件发生，投资组合的值都是相同的．这意味着投资组合在这段时间内实际上是无风险资产，因此，这个投资组合应该与到期日为T+1的零息债券有相同的回报，由此引出2个条件

uYt(τ)Pt(τ+1)+HuYt(τ″)Pt(τ″+1)=

dYt(τ)Pt(τ+1)+HdYt(τ″)Pt(τ″+1)

(1)

W(t)=Pt(1)W(t+1)

(2)

式(2)可改写为

Pt(τ+1)+HPt(τ″+1)=

dYt(τ)Pt(τ+1)+HdYt(τ″)Pt(τ″+1)

(3)

由式(1)和式(3)具有相同的H值，故可得

ptuYt(τ″)+(1-pt)dYt(τ″)=1．

(4)

除了概率过程pt随着时间变化，最后的结果与Ho-Lee模型相同．过程pt的取值依赖于Yt而不依赖于τ， 对于Yt的每个可能值都有ptuYt(τ)+(1-pt)dYt(τ)=1．

推论1

Pt(τ″+1)= Pt(1)[ptuYt(τ″)Pt(τ″+1)Pt(1)+

(5)

由此说明t时刻零息债券的价值仅仅是t+1时刻可能价值折现的平均．

1.4最小熵鞅测度

在套利策略定义中，有关期望是在物理概率测度之下取得的，为建立鞅概率测度，需用到等价测度的概念．

(6)

则对于所有的t, Dt>0, E[Dt]=1且

这些结论允许Dt可以作为一个密度过程，这个过程将被用于介绍等价测度．

Pt(τ+1)

定理4过程pt给出在等价鞅测度*下，期限结构在t时刻向上移动的概率，即pt=]．

本研究采用最小熵鞅测度(minimal entropy martingale measure， MEMM)的方法确定1个风险中性轮换概率矩阵．实际上，对于不完备市场中的期权定价，MEMM是一种受欢迎的方法，其基本思想是选取一个等价的鞅测度使这个等价鞅测度和物理概率测度之间的相对熵最小，即两个概率测度之间的距离最小．

如果在所有等价鞅测度的集合中，测度Q使相对熵最小，则称Q为最小熵鞅测度．

定理5最小熵鞅测度的特征为

(7)

这是一个有约束的最优化问题，应用拉格朗日乘数法.令

(8)

根据式(8)及对λ和γ的偏导数得

exp(1+λ)

(9)

exp(1+λ)

(10)

混合式(9)和式(10)得

exp(-γdY0)=

(11)

由归纳法得拉格朗日乘数的表达式为

1.5二叉树模型的拓展

经典Ho-Lee模型构造的二叉树期权定价中，假设零息债券的价格函数从1个状态到另1个状态的演化只依赖向上运动的数量，不依赖发生的顺序．根据路径独立性得到向上和向下参数的明确表达式．本节旨在讨论市道轮换下的路径独立性．

【证】 对于第1条路径有

令上述两式相等得

(12)

(13)

此结果恰好类似经典的Ho-Lee模型．定义

(14)

将式(14)代入式(13)得1个简单的差分方程．已知uYt(0)=1， 用迭代法得uYt和dYt的解

(15)

f(pj)=0

f(pj)= p2j(1-δj)(1-δτj)(pi+(1-pi)δτ+1i)+

(16)

【证】 将模型用于第1条路径得

将模型用于第2条路径得

Pt+3(τ)=

令上述两式相等得

(17)

根据式(15)得式(18)，其对每个τ都成立

(18)

重新排序各项即得期望的结果．

如果固定pi、 δi和δj， 方程(16)得到一个关于pj的二次方程系统(对于每个τ)．因为给定的这些方程的系数依赖于τ， 所以它们是不相同的．一个解pj∈(0,1)是否能同时解出所有方程尚不清楚．那么是否可以找到一个条件，使得在这个条件下，解pj∈(0,1)存在呢？下面定理可提供部分答案．

定理7假设δi=δj， 则给定pi， 方程(16)的系统至少存在一个解pj．

【证】 固定δi=δj， 则对每个τ， 给定pi(pi∈(0,1))的任何值，都至少存在一个解pj且pj=pi， 从方程(18)可见，这是显然的．

尽管有定理7，情况仍不理想．因为在δi≠δj时，二次方程解的存在性仍不清楚．事实上，唯一保证可行的模型是pi=pj且δi=δj时的模型，此时对于所有的(i, j)和τ， 都有ui=uj且di=dj， 即期限结构在所有状态的演化都由相同的值控制，这就如同只有1种状态．总之，在市道轮换存在时，唯一保证可行的模型是每个状态的期限结构都相同的模型，然而此时整个市道轮换结构变得没有意义．为使市道轮换存在实际意义，在存在市道轮换时不能应用路径独立的条件．

2数值举例

本节主要提供一些在马氏和半马氏轮换情形下模型应用的简单例子，目的是在这些框架下使用模型去定价一些资产．

建立四周期(包括零时)两状态模型．假设Y0=1, K0=3， 如经典的Ho-Lee模型，必须指定一些参数(即本例中每个状态的值)和初始期限结构．对于轮换的Ho-Lee模型，给出参数值为p1=0.6, p2=0.5, δ1=0.97, δ2=0.95， 零息债券的一组初始价格值为P0(0)=1.000, P0(1)=0.952, P0(2)=0.878, P0(3)=0.823． 目标是在到期日为t=3的零息债券上定价到期日为t=2， 行权价为s=0.94的1个欧式期权．本研究将在马氏和半马氏框架下做到这一点，且选择最小熵鞅测度作为定价测度．根据选取的参数值，得到零息债券的价格演化如图2．图2仅呈现了前3个时期，最后1个时期债券的价格等于1．

图2　零息债券价格的演化Fig.2　Evolution of zero-coupon bond prices

2.1马氏轮换框架

考虑1个两状态马氏链，转移概率矩阵为

定义qij(t)=因为这个量完全定义了1个半马氏核．若qij(t)满足

下面期权价格树的某些分枝上标记的值是从1个节点到下1个节点的轮换概率，仅标记了本例中有用的值．

图3　马氏轮换框架下债券期权价格的演化Fig.3　Evolution of bond option prices under Markov regime switching framework

2.2半马氏轮换框架

类似马氏轮换框架，记qij(t)=

对于时间的分布，本研究使用1个离散时间威布尔分布[19]，根据文献[19]有

qij(0)=0 且

定义常数α12=0.2, β12=0.5, α21=0.4, β21=0.6． 使用最小熵鞅测度的特征和与马氏情形下相同的后向诱导法，得期权价格树如图4．

图4　半马氏轮换框架下债券期权价格的演化Fig.4　Evolution of bond option prices under semi-Markov regime switching framework

由图3和图4可知，马氏轮换框架和半马氏轮换框架得到的期权价格有很大区别，这归因于轮换概率不同．

选取最小熵鞅测度作为定价测度时，半马氏轮换有以下优点：① 马氏轮换过程具有无记忆性，只与当前期的状态有关. 半马氏轮换不需要无记忆性，使离散时间期限结构模型更贴近现实.② 轮换过程中转移状态相同时，马氏轮换保持常数轮换概率，而半马氏轮换的概率与状态持续时间有关.③ 实证表明轮换过程对经济周期呈持续性依赖，马氏轮换模型不能体现这个特征，而半马氏轮换中通过半马氏过程对后向回复时间的依赖充分体现了这一点．

结语

本研究采用金融工程的无套利理论与方法，分析半马氏市道轮换条件下基于利率期限结构的债券期权定价问题，提出的模型使离散时间期限结构模型更贴近现实．所建立模型与无套利概念相一致，且无套利与鞅测度概念的联系得到说明．通过最小熵鞅测度来处理市场的不完备性，给出这个测度的一个明显特征，这个特征在模型的实际应用中非常有用．本模型可以推广到三叉树模型的情形，同时可以讨论带跳的零息债券定价问题.

引文：柳向东，王星蕊. 最小熵鞅测度下的半马氏市道轮换利率模型[J]. 深圳大学学报理工版，2016，33(2)：154-163.

参考文献/ References：

[1] Ho T S Y, Lee S B. Term structure movements and pricing interest rate contingent claims[J]. Journal of Finance, 1986, 41(5): 1011-1029.

[2] Vasicek O. An equilibrium characterization of the term structure[J]. Journal of Financial Economics, 1977, 5(2):177-188.

[3] Cox J, Ingersoll Jr J , Ross S , et al. A theory of the term structure of interest rates[J]. Econometrica, 1985, 53(2): 385-408.

[4] Hull J, White A. Pricing interest-rate derivative securities[J]. Review of Financial Studies, 1990, 3(4): 573-592.

[5] Goldfeld S M, Quandt R E. A Markov model for switching regressions[J]. Journal of Econometrics, 1973, 1(1): 3-16.

[6] Hamilton J D. A new approach to economic analysis of non-stationary time series and the business cycle[J]. Econometrica, 1989, 57(2): 357-384.

[7] Di Masi G B, Kabanov Y M, Runggaldier W J, et al. Mean-variance hedging of options on stocks with Markov volatilities[J]. Theory of Probability and Its Applications, 1994, 39(1): 211-222.

[8] Elliott R J, Van der Hoek J. An application of hidden Markov models to asset allocation problems[J]. Finance and Stochastics, 1997, 1(3): 229-238.

[9] Elliott R J, Chan L, Siu T K, et al. Option pricing and Esscher transform under regime switching[J]. Annals of Finance, 2005, 1(4): 423-432.

[10] Jobert A, Rogers L C G. Option pricing with Markov-modulated dynamics[J]. Siam Journal on Control and Optimization, 2004, 44(6): 2063-2078.

[11] Kijima M, Yoshida T. A simple option pricing model with Markovian volatilities[J]. Journal of the Operations Research Society of Japan, 1993, 36(3): 149-166.

[12] Silvestrov D, Stenberg F. A pricing process with stochastic volatility controlled by a semi-Markov process[J]. Communications in Statistics: Theory and Methods, 2004, 33(3): 591-608.

[13] Dahlquist M, Gray S F. Regime switching and interest rates in the European monetary system[J]. Journal of International Economics, 2000, 50(2): 399-419.

[14] Diebold F, Rudebusch G. A nonparametric investigation of duration dependence in the American business cycle[J]. Journal of Political Economy, 1990, 98(3): 596-616.

[15] Hong Yongmiao, Li Haitao. Nonparametric specification testing for continuous-time models with applications to term structure of interest rates[J]. Review of Financial Studies, 2005, 18(1): 37-84.

[16] D’Amico G, Manca R, Salvi G, et al. A semi-Markov modulated interest rate model[J]. Statistics & Probability Letters, 2013, 83(9): 2094-2102.

[17] Ghosh M K, Goswami A . Risk minimizing option pricing in a semi-Markov modulated market[J]. Siam Journal on Control & Optimization, 2009, 48(3):1519-1541.

[19] Limnios N, Barbu V S. Semi-Markov chains and hidden semi-Markov models toward applications[M]. New York, USA: Springer-Verlag, 2008.

[20] Chryssaphinou O, Karaliopoulou M, Limnios N, et al. On discrete-time semi-Markov chains and applications in word occurrences[J]. Communications in Statistics: Theory and Methods, 2008, 37(8):1306-1322.

[21] D’Amico G, Janssen J, Manca R, et al. European and American options: the semi-Markov case[J]. Physica A: Statistical Mechanics and Its Applications, 2009, 388(15): 3181-3194.

[22] Ratanov N. Option pricing under jump-diffusion processes with regime switching[J]. Methodology and Computing in Applied Probability, 2015: 1-17.

[23] 柳向东, 何远兰. 二叉树模型的测度变换及应用[J]. 暨南大学学报自然科学版, 2010, 31(1):4-6.

Liu Xiangdong, He Yuanlan. The measure transformation of the binomial model and its application[J]. Journal of Jinan University Natural Science, 2010, 31(1):4-6.(in Chinese)

[24] 柳向东, 唐颖. 半马氏过程框架下的期权定价[J]. 暨南大学学报自然科学版, 2011, 32(1):10-13.

Liu Xiangdong, Tang Ying. Option pricing under Semi markov process[J]. Journal of Jinan University Natural Science, 2011, 32(1):10-13.(in Chinese)

[25] 柳向东, 郭慧. 基于市道轮换模型的SHIBOR市场利率[J]. 深圳大学学报理工版, 2015, 32(3): 317-323.

Liu Xiangdong, Guo Hui. Research of market interest rates of the SHIBOR based on regime switching model[J]. Journal of Shenzhen University Science and Engineering, 2015, 32(3):317-323.(in Chinese)

【中文责编：方圆；英文责编：木南】

Semi-Markov regime switching interest rate models under minimal entropy martingale measure

Liu Xiangdong†and Wang Xingrui

College of Economics, Jinan University, Guangzhou 510632, Guangdong Province, P.R.China

Abstract：In this paper, we discussed the evolution of the prices of zero-coupon. On the basis of Ho-Lee model, a discrete time regime switching binomial model of the term structure where the regime switches are governed by a discrete time semi-Markov process is introduced by applying the arbitrage free principle and martingale measure method. This paper use minimal entropy martingale measure (MEMM) to deal with the above model, and give an application to the pricing of a European bond option in Markov and semi-Markov regime switching framework．

Key words：application of statistical mathematics; Ho-Lee model; arbitrage free method; binary tree model; term structure of interest rate; minimal entropy martingale measure; bond option pricing

作者简介：柳向东(1973—)，男，暨南大学教授、博士生导师. 研究方向：概率统计在经济金融领域的应用研究. E-mail: tliuxd@jnu.edu.cn

基金项目：国家自然科学基金资助项目(71471075)；教育部人文社会科学研究资助项目(14YJAZH052)

中图分类号：O 211.9

文献标志码：A

doi：10.3724/SP.J.1249.2016.02154

Received：2015-11-08；Accepted：2016-01-10

Foundation：National Natural Science Foundation of China(71471075) ; Humanities and Social Science Foundation of Ministry of Education of China(14YJAZH052)

† Corresponding author：Professor Liu Xiangdong. E-mail: tliuxd@jnu.edu.cn

Citation：Liu Xiangdong，Wang Xingrui. Semi-Markov regime switching interest rate models under minimal entropy martingale measure[J]. Journal of Shenzhen University Science and Engineering, 2016, 33(2): 154-163.(in Chinese)

【应用数学 / Applied Mathematics】