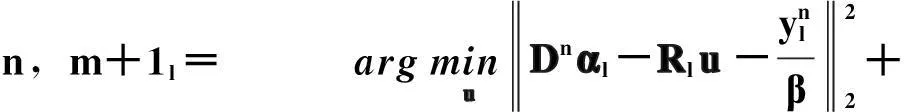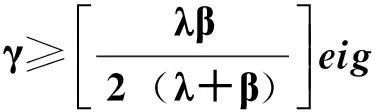基于加权双层Bregman及图结构正则化的磁共振成像
2016-04-26张明辉卢红阳徐晓玲
张明辉,肖 凯,卢红阳,徐晓玲
南昌大学信息工程学院,江西南昌330031
基于加权双层Bregman及图结构正则化的磁共振成像
张明辉,肖凯,卢红阳,徐晓玲
南昌大学信息工程学院,江西南昌330031
摘要:针对磁共振图像(magnetic resonance imaging, MRI)重建质量的问题,提出一种基于加权双层Bregman字典学习方法和图结构正则化稀疏表示的新算法.该算法中,迭代重加权最小l1和图结构正则化稀疏表示模型是被合并到双层Bregman字典学习方法中.加权双层Breman的字典学习方法在外层迭代中增强K空间抽样数据的约束性,在内层迭代中解决Lp的优化.而图结构正则化稀疏表示方法具备捕获图像结构细节的能力,所以从较高的欠采样数据中能完成精确重建.此外,在内层迭代中,重加权最小l1和图结构正则化稀疏表示使算法能快速地趋于收敛.实验结果表明,所提出的算法可有效恢复MRI图像,其峰值信噪比和高频错误的值都优于基于压缩感知的字典学习方法和基于双层Bregman的自适应字典学习方法.
关键词:图像处理;磁共振成像;压缩感知;图结构正则化稀疏表示;字典学习;加权双层伯格曼迭代;交替方向法
在医学研究和临床诊断方面,磁共振成像(magnetic resonance imaging, MRI)做出了巨大贡献,并在该领域扮演着重要角色.然而,尽管MRI技术对人体非侵入和非电离,而且能够提供无与伦比的高质量成像,但其缓慢的扫描时间,会导致病人产生不舒适感[1],大幅增加成像过程中产生伪影的机会,从而降低了成像质量.所以,如何在减少扫描时间的同时又能获取高分辨率的重构是研究人员致力于MRI医学研究的重大课题.
近年,压缩感知(compressed sensing)因具稀疏正则化特征,且能远低于奈奎斯特采样频率进行抽样[2]在信号处理领域备受关注.压缩感知在磁共振上的应用(简称CS-MRI[3-8]),能够减少扫描的时间,并保证重建效果高效.目前,基于压缩感知理论的基础,人们提出了很多算法,例如,小波阈值方法[5]和全变差(total variation, TV)方法[8-10]等,这些传统的方法通过使用预先重建好的字典进行重构[1,12-15],导致重构后的图像具有一些缺陷.其中,TV模型的分段式图像重构,不能获取图像的细节信息,所以在临床诊断中难以适用;而小波阈值方法在重建图像时会出现伪迹.Ravishankar等[16]提出基于压缩感知的字典学习(dictionary learning for compressed sensing, DLMRI)方法,该方法使每个图像块都能稀疏表示,可分为两步实现:① 设计自适应的学习字典;② 通过高欠采样K空间数据[18]来重建图像.这种基于图像块稀疏表示模型的方法[17-18]在现阶段应用甚广.Liu等[17]提出基于双层Bregman的自适应字典学习(two-level Bregman method with dictionary updating, TBMDU)方法,该方法在外层迭代中用于数据的约束,而在内层致力于字典更新和图像块的稀疏表示,从而对磁共振成像能够实现更好的重建,效果较之前所提出的字典学习方法更佳.Candès等[19]提出一种迭代的加权1范数的优化算法,该算法能够线性优化全变差的惩罚,它比1范数在迭代过程中要表现的更优秀.Zheng等[20]在图像表示方面,提出图结构正则化稀疏表示,能很好地捕获数据局部的多样化结构.
本研究基于TBMDU模型和迭代的加权1范数以及图结构正则化稀疏表示的理论,构造基于加权双层Bregman方法及图结构正则化的磁共振成像重建(weighted two-level Bregman method with graph regularized for MRI reconstruction, WTBMGR)方法.在该算法中,加权双层伯格曼的应用能够很好地减轻TV算法中出现的问题,也能减少计算量.而融入图结构正则化稀疏表示后,对于图像重建质量和计算效率方面都有了很大的提高.
1理论研究
1.1TBMDU算法
Liu等[17]提出的TBMDU算法对磁共振图像的重建分为内外两层,外层用于加强K空间数据的约束,而内层致力于字典更新和图像块的稀疏表示.该方法对图像重建的质量及速度都有明显提升.
Bregman迭代的两个重要的字典更新步骤为
(1)
其中, k为迭代次数; u为N像元的2维复合图像, u∈N,为像素集合; J(u)为稀疏模型; μ是权重系数, μ>0; Fp为部分傅里叶编码矩阵, Fp∈N×Q, Fpu=f; f为Q维的欠采样的傅立叶测量值.
在TBMDU方法中,以稀疏模型

作为正则项,将其代入式(1)可得

uk+1= argminuminD,S∑lαl1+λ2Dαl-Rlu22æèçöø÷+μ2Fpu-fk22æèçöø÷fk+1=fk+f-Fpuk+1{
(2)其中, D=[d1, d2, …, dJ]∈M×J为学习的字典矩阵, M为图像块的个数, J=KM, K表示过完备字典的度; S=[α1, α2, …, αL]∈J×L, 表示理想中的稀疏系数矩阵, L为稀疏系数的个数;Rlu为的图像块,每个图像块都能用字典D来稀疏表示.
此外,在字典更新过程中,系数λ用于平衡图像块的稀疏程度和其发生过程中所产生的误差,该系数具有很好的鲁棒性.
1.2图结构正则化稀疏表示的方法
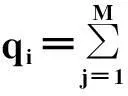

(3)
简单来说,图结构正则化稀疏表示的目标函数是由3部分组成:经验缺失项、拉格朗日正则项和基于1范数的稀疏惩罚项,即


(4)
其中, λ为数据一致性程度的相关性参数; θ为图结构正则化系数; X为数据项;下标F表示傅里叶编码矩阵.
2WTBMGR方法
根据前面的先验知识,提出基于加权Bregman方法以及图结构正则化稀疏表示的磁共振成像重建(WTBMGR)算法.该算法模型能够有效地解决接近p范数惩罚模型,在系数矩阵环节,有更好的稀疏作用,使其更稀疏.此外,也能很好地解决混叠效应,从而更好地重建图像.其目标函数为

uk+1= argminuminD,S∑l1pαlp+λ2Dαl-Rlu22+θtr(SNST)æèçöø÷+μ2Fpu-fk22æèçöø÷fk+1=fk+f-Fpuk+1{
(5)
其中,正则项为
J(u)=
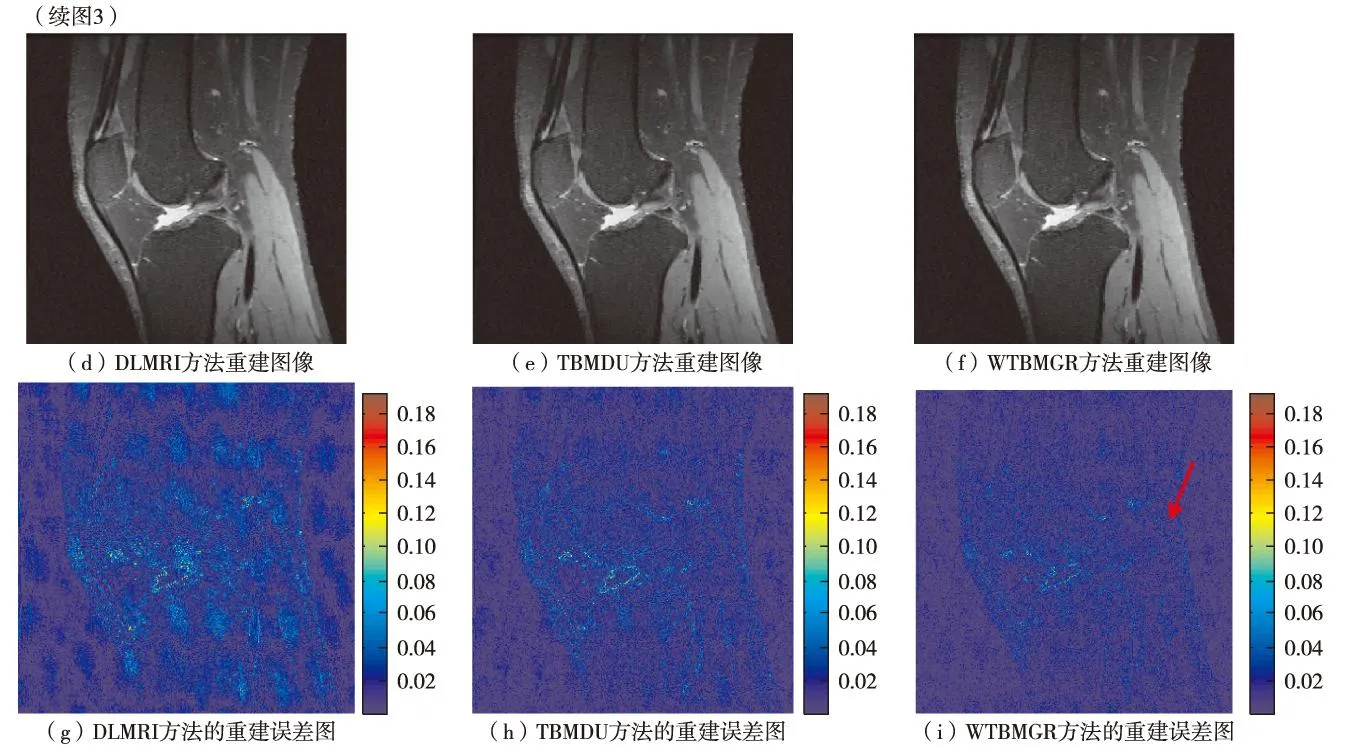
这里, p的取值范围为0 在字典更新环节,利用加权双层Bregman方法解式(5),然后把一个约束式子转变成不受约束的式子 (6) 其中,Al为辅助变量,把不受约束的式子转换成受约束的式子. 通过解一系列的子问题,得到字典更新规则 Dn+1=Dn+ξYn+1(Sn+1)T (7) 以及 yn+1l=ynl+β(Rlu-Dn+1αn+1l-An+1l) (8) 其中, Dn为外层迭代中更新的字典, n表示在外层字典更新中的迭代次数; ξ与β为外层迭代中的拉格朗日系数; yl为Y的元素, yl为外层迭代中的中间量,用来表示D与 Al的关系. 在稀疏表示步骤,通过先验知识[17,20],能得到更新的系数为 α n,m+1l= argminuDnαl-Rlu-ynlβ22+ θNiiαTlαl+αTlhi+ (9) 其中, αl为稀疏系数, m表示内层迭代的次数; Nii为位置点i=j处的值; hi=2∑j≠iNijbj; αj,l为位置j处的稀疏系数. 利用门限法,通过求解式(9)得到稀疏系数的矩阵αl. α n,m+1l= argminαlγαl-αn,ml+-2θNiiαml-hml+(Dk)Tym+1l2γéëêêùûúú22+2λ+βλβWn,mlαl1æèçöø÷= (10) 在每次内层迭代过程中,通过消除变量D、 S和 A来更新 u. u k+1= argminu∑jμ2Fpu-fk22+ (11) 用最小二乘法求解 u, 计算公式为 (12) (13) 其中, kx和ky为K空间中相应的坐标点; ω为重叠块在对应像素的重复次数; Iv为单位矩阵. 于是可得 Fu(kx,ky)= (14) 其中, Ω为已采样数据的子集; Fu表示更新的K空间数据值. 3实验数据分析与处理 在不同采样因子和不同采样轨迹的条件下,用所得到的实验数据来评估本研究提出的算法.在相同的环境条件下,用方法WTBMGR和TBMDU、DLMRI作比较.其中,采样轨迹包括二维随机采样[6]、笛卡尔采样[1,16]和伪径向采样[6,16].图像大小为512×512,设置图像块M=6, 过完备字典K=1, 块重叠r=1, 数据样本大小L=267 289, 字典大小J=36. 设ε的初值为5,每次迭代过后,在原基础上减少2%.此外,通过峰值信噪比(peak signal-to-noise ratio, PSNR)和高频错误(high-frequency error norm, HFEN)来量化图像重建的质量. 图1中,在比较相同采样轨迹(二维随机采样)条件下,改变采样因子(2.5、4.0、6.0、8.0、10.0和20.0)时,DLMRI、TBMDU和WTBMGR的峰值信噪比PSNR和高频错误HFEN.其中,图1(a)为输入图像;图1(b)和图1(c)分别是其对应的PSNR和HFEN变化曲线图;图1(d)至图1(f)依次是上述方法在采样因子为8时的重建图像;图1(g)至图1(i)则依次为3种方法的重建误差图.由图1可见,WTBMGR算法在成像质量及重建误差方面明显好于DLMRI和TBMDU;通过对比PSNR和HFEN,WTBMGR算法在不同的采样因子下,其PSNR值高于另外两种方法,HFEN值则更低. 图1 在相同二维随机采样轨迹和不同采样因子下的结果Fig.1 Reconstruction results under the same 2D random sampling and different undersampling factors 图2中,在相同的采样因子(=7.14)和相同的采样轨迹(二维随机采样)下,添加混合高斯白噪声(标准方差分别为2.0、5.0、8.0、10.0和14.2)时,采用DLMRI、TBMDU和WTBMGR算法的重构图像和对应的误差图.其中,图2(a)为输入图像;图2(b)为采样因子为7.14时的二维随机采样轨迹图;图2(c)为3种方法的PSNR值曲线图,由图可见,采用WTBMGR方法重构图像的PSNR值要高于另外2种方法;图2(d)至图2(f)依次为3种方法在标准方差为8时的成像结果;图2(g)至图2(i)依次为3种方法对应的误差图. 图2 在相同采样因子7.14和相同二维随机采样轨迹下,添加混合高斯白噪声的结果Fig.2 Reconstruction results for the same 7.14-fold undersampling and 2D random sampling under different levels of complex white Gaussian noise added 图3 在相同采样因子7.14和不同采样轨迹下的成像结果Fig.3 Reconstruction results under the 7.14-fold undersampling and different sampling trajectories 图3 在相同采样因子7.14和不同采样轨迹下的成像结果Fig.3 Reconstruction results under the 7.14-fold undersampling and different sampling trajectories 图3中,在相同的采样因子下,改变采样轨迹,比较DLMRI、TBMDU和WTBMGR的成像情况.图3(a)是输入图像,图3(b)和图3(c)分别为在采样因子=7.14下的笛卡尔采样和伪径向采样.图3 (d) 、图3 (e) 和图3 (f)分别为3种方法在伪径向采样下的成像结果,图3(g)、 图3(h)和图3(i)分别为其误差图.表1为3种方法在采样因子为7.14和不同采样轨迹下的PSNR值比较. 表1 在相同采样因子7.14和不同采样 图4 在相同采样因子为5和笛卡尔采样轨迹下的复数实验Fig.4 The complex-valued data under the same 5-fold undersampling and the same Cartesian sampling trajectory 在图4中,呈现了一个复数实验,用来评估磁共振成像系统的分辨率.在相同的采样因子(采样因子=5)和相同的采样轨迹(笛卡尔采样)下,通过对比DLMRI和TBMDU算法,来证明算法WTBMGR的优势.通过实验可得,DLMRI和TBMDU的峰值信噪比分别为18.50和21.37 dB,而WTBMGR的峰值信噪比为22.89 dB.同样,WTBMGR在成像质量方面也要明显好于另外2种方法.图4(a)是输入图像,图4(b)、 图4(c)和图4(d)分别为DLMRI、TBMDU和WTBMGR算法的成像结果,图4(e)为图4(a)至图4(d)各自的部分放大图.截取的部分图像,横坐标是370至480像素处,对应的纵坐标为150至260像素处. 结语 本研究提出基于加权Bregman方法以及图结构正则化稀疏表示的磁共振成像重建算法.该算法能很好的增强K空间数据的约束性,有着高效的字典更新,能自适应地增强和捕获图像局部结构特征,实现完成更优质的磁共振图像重建.实验证明,该算法在图像重建质量和数值比较上都明显优于DLMRI和TBMDU算法. 引文:张明辉,肖凯,卢红阳,等.基于加权双层Bregman及图结构正则化的磁共振成像[J]. 深圳大学学报理工版,2016,33(2):119-126. 参考文献/ References: [1] Lustig M, Donoho D, Pauly J M. Sparse MRI: the application of compressed sensing for rapid MR imaging[J]. Magnetic Resonance in Medicine, 2007, 58(6): 1182-1195. [2] Donoho D. Compressed sensing[J]. IEEE Transactions on Information Theory, 2006, 52(4): 1289-1306. [3] Wang Yanhua, Ying L. Compressed sensing dynamic cardiac cine MRI using learned spatiotemporal dictionary[J]. IEEE transactions on Biomedical Engineering, 2014, 61(4): 1109-1120. [4] Caballero J, Price A N, Rueckert D, et al. Dictionary learning and time sparsity for dynamic MR data reconstruction[J]. IEEE Transactions on Medical Imaging, 2014, 33(4): 979-994 [5] Ma Shiqian, Yin Wotao, Zhang Yin, et al. An efficient algorithm for compressed MR imaging using total variation and wavelets[C]// IEEE Conference on Computer Vision and Pattern Recognition. Anchorage, USA: IEEE, 2008:1-8. [6] Wong A, Mishra A, Fieguth P, et al. Sparse reconstruction of breast MRI using homotopic L0minimization in a regional sparsified domain[J]. IEEE Transactions on Biomedical Engineering, 2013, 60(3): 743-752. [7] Lingala S G, Jacob M. Blind compressive sensing dynamic MRI[J]. IEEE Transactions on Medical Imaging, 2013, 32(6): 1132-1145. [8] Zhang Y, Dong Z, Wang G J S. An improved reconstruction method for CS-MRI based on exponential wavelet transform and iterative shrinkage/thresholding algorithm[J]. Journal of Electromagnetic Waves & Applications, 2014, 28(18): 2327-2338. [9] Selesnick I W, Chen P Y. Total variation denoising with overlapping group sparsity[C]// IEEE International Conference on Acoustics, Speech, and Signal Processing (ICASSP). Vancouver, Canada: IEEE, 2013: 5696-5700. [10] Rudin L I, Osher S, Fatemi E. Nonlinear total variation based noise removal algorithms[J]. Physica D: Nonlinear Phenom, 1992, 60(1/2/3/4): 259-268. [11] Abraham A, Dohmatob E, Thirion B, et al. Extracting brain regions from rest fMRI with total-variation constrained dictionary learning[J]. Medical Image Computing and Computer-Assisted Intervention, 2013, 16(2): 607-615. [12] Qu Xiaobo, Guo Di, Ning Bende, et al. Undersampled MRI reconstruction with patch-based directional wavelets[J]. Magnetic Resonance Imaging, 2012, 30(7): 964-977. [13] Guerquin-Kern M, Haberlin M, Pruessmann K, et al. A fast wavelet-based reconstruction method for magnetic resonance imaging[J]. IEEE Transactions on Medical Imaging, 2011, 30(9): 1649-1660. [14] Kim Y, Nadar M S, Bilgin A. Wavelet-based compressed sensing using a Gaussian scale mixture model[J]. IEEE Transactions on Image Processing, 2012, 21(6): 3102-3108. [15] Qiu Chenlu, Lu Wei, Vaswani N. Real-time dynamic MR image reconstruction using Kalman filtered compressed sensing[C]// IEEE Internal Conference on Acoustics, Speech and Signal Processing. Taipei, China: IEEE, 2009: 393-396. [16] Ravishankar S, Bresler Y. MR image reconstruction from highly undersampledk-space data by dictionary learning[J]. IEEE Transactions on Medical Imaging, 2011, 30(5): 1028-1041. [17] Liu Qiegen, Wang Shanshan, Yang Kun, et al. Highly undersampled magnetic resonance imaging reconstruction using two-level Bregman method with dictionary updating[J]. IEEE Transactions on Medical Imaging, 2013, 32(7): 1290-1301. [18] Liu Qiegen, Wang Shanshan, Luo Jianhua. A novel predual dictionary learning algorithm[J]. Journal of Visual Communication Image Representation, 2012, 23(1): 182-193. [19] Candès E J, Wakin M B, Boyd S P. Enhancing sparsity by reweighted l1minimization[J]. Journal of Fourier Analysis and Applications, 2008, 14(5/6): 877-905. [20] Zheng Miao, Bu Jiajun, Chen Chun, et al. Graph regularized sparse coding for image representation[J]. IEEE Transactions on Image Processing, 2011, 20(5): 1327-1336. 【中文责编:英子;英文责编:雨辰】 Weighted two-level Bregman method with graph regularized sparse coding for MRI reconstruction Zhang Minghui†, Xiao Kai, Lu Hongyang, and Xu Xiaoling School of Information Engineering, Nanchang University, Nanchang 330031, Jiangxi Province, P.R.China Abstract:To improve the quality of magnetic resonance imaging, we propose a new dictionary learning algorithm integrating the weighted two-level Bregman and graph regularized sparse coding. We incorporate the iteratively reweighted l1-minimization and graph regularized sparse coding model into the two-level Bregman method with dictionary updating (TBMDU). The weighted two-level Bregman iterative procedure enforces the constraints of K-space sampled data in the outer-level and solves Lp-optimization in the inner-level. The graph regularized sparse coding model has great capacity in capturing structural details of images and, consequently, enables accurate reconstruction from highly under-sampled data. Furthermore, the proposed algorithm is able to converge with a relatively small number of iterations due to the reweighted l1-minimization iteration and graph regularized sparse coding applied in the inner minimization. Simulation results demonstrate that the proposed algorithm can reconstruct MRI images efficiently and outperforms some current approaches, such as dictionary learning for compressed sensing and two-level Bregman method with dictionary updating, in terms of the peak signal-to-noise ratio and the norm value of high-frequency error. Key words:image processing; magnetic resonance imaging; compressed sensing; graph regularized sparse coding; dictionary learning; weighted Bregman iterative method; alternating direction method 作者简介:张明辉(1963—),男,南昌大学教授.研究方向:压缩感知,磁共振成像.E-mail: zhangmh3529@163.com 基金项目:国家自然科学基金资助项目(61362001);江西省自然科学基金资助项目 (20151BAB207007) 中图分类号:N 34 文献标志码:A doi:10.3724/SP.J.1249.2016.02119 Received:2015-12-10;Accepted:2016-02-16 Foundation:National Natural Science Foundation of China (61362001); Natural Science Foundation of Jiangxi Province (20151BAB207007) † Corresponding author:Professor Zhang Minghui. E-mail: zhangmh3529@163.com Citation:Zhang Minghui,Xiao Kai,Lu Hongyang,et al. Weighted two-level bregman method with graph regularized sparse coding for MRI reconstruction[J]. Journal of Shenzhen University Science and Engineering, 2016, 33(2): 119-126.(in Chinese) 【电子与信息科学 / Electronics and Information】