浅折中学数学数学的逻辑特点及解题思维路径



浅折中学数学数学的逻辑特点及解题思维路径

◇山东刘伦明

中学数学的教学在所有学科中占据重要的地位,不仅影响着学生逻辑思维的养成和抽象能力的提升,而且很大程度上决定了学生成绩的好坏,因此加强学生数学的学习很有必要．在数学解题中既要注重观察各已知条件间的逻辑关系，也要注重思维能力的提升,举一反三,养成良好的解题习惯．本文以函数问题为例进行说明.

1函数教学的逻辑特点

1.1低级到高级的渐进式教学

函数部分是中学数学的中枢,也是连接高中数学各部分内容的桥梁,从函数教学的整体来看,其逻辑能力的体现是从具体到抽象、低级到高级阶梯型发展．如果对前一阶段函数定义、性质的理解不透彻，必然会影响到下一阶段函数的学习．从一次函数到二次函数、三角函数到反三角函数等,都是一个从低级到高级、具体到抽象的概括过程．

1.2定义域优先考虑的逻辑特点

自变量的取值范围称作函数的定义域,在后续教学中有关函数的性质或运算都是以函数定义域为基础进行的,这是函数特有的逻辑形式,只要弄清楚函数的定义域,那无论是求解析式还是求值域,都可以迎刃而解．

1.3具体到抽象的理论

函数教学是数学教学中逻辑性较强的部分,每一个函数概念、命题都需经过严密推导论证才能成为定理,但是深入学习会发现函数的定义越来越抽象,实例也越来越难找,甚至无法明确地指出函数的图象等,只能运用一般性的抽象概括描述．

2函数问题解题思维路径

2.1多种方法互换的解题路径

针对同一道函数题,采用不同的视角往往可以得到多种不同的解题思路.在教学过程中教师应充分考虑到题目特征,尽量运用多种思维方式来解答题目,不仅有助于拓宽学生的知识面,发散学生的思维能力,还能让学生复习到更多的知识点,提高学生分析问题的能力．

方法1利用二次函数思想.将x2+y2用x或y表示出来得到一个一元二次函数,由于x的范围确定,根据二次函数的图象与性质易得出结果.

方法2假设x=2+t,y=2-t,这样所求式就变成了关于t的一个一元二次函数,同样根据t的范围易得出结果.

方法3利用几何法.题目可以转化成求已知线段到原点的最大和最小距离,通过在坐标系中作图即可快速得出结果．

多种解题思路有助于培养学生应变能力和形成发散思维,增强变形题时联想分析能力．也省去了教师备课中列举大量习题的麻烦,提高了备课效率,让学生能对所学知识融会贯通、举一反三．

2.2“分解式”解题路径

“分解式”思维主要适用的对象是一些结构复杂、解题难度较大的函数证明题．学生在面对这一类型题目时,往往不知从何入手．“分解式”思维就是将这些难题分解成几道比较简单、易于解答的新题,通过对新题解题思路的研究来启发原题的解题思路,以简驭繁,达到解出原题的目的．如下面这道函数证明题目.

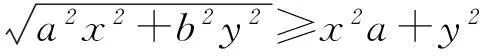
2.3数形结合式函数解题思路

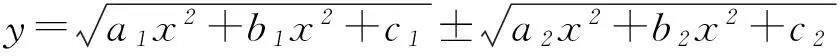
中学数学的教学看似只是由一个个公式和符号串联而成,实际上也需要扎实的逻辑表述能力和逻辑素养,这样学生才能更容易理解题目中蕴含的内在逻辑联系、养成良好的解题习惯，从而提升解题速度．

(作者单位：山东省福山区第一中学)