利用直线参数方程解两类常见题



利用直线参数方程解两类常见题

李东进

(江苏省苏州新草桥中学，215011)

众所周知，平面内过定点P0(x0,y0)、倾斜角为α的直线l的参数方程的标准形式为

一、解决椭圆中弦对张直角问题

以椭圆中弦对中心张直角为背景的试题在高考、各地高考模拟试卷中经常出现,由于计算繁杂,解决起来并不轻松．若能利用直线的参数方程可将繁杂的计算转化成关于角α的代数式,再利用三角函数知识就可以计算出结果．

证明设直线OA的方程为

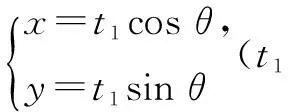
代入椭圆方程，得

b2t21cos2θ+a2t21sin2θ=a2b2.

设直线OB的方程为

代入椭圆方程，得

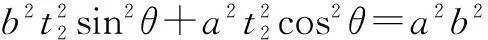
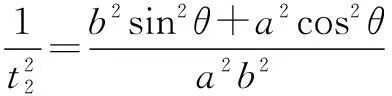
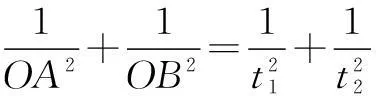
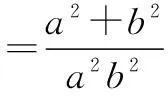
一是依据短板效应原理，对各评价因子各分级进行分类赋值（见表2）。其中，强限制性因子具有“一票否决”作用，直接赋值为禁止建设区；较强限制性因子，采用专家咨询法分别赋值为适宜、有条件适宜、不适宜。

(1)求椭圆E的方程;

(2)过原点O任作两条相互垂直的射线交椭圆E于P、Q两点,试判断直线PQ是否总与圆O相切,并说明理由.

二、解决椭圆上四点共圆问题

圆是数学中优美的图形,具有丰富的性质．其中圆锥曲线上四点共圆的相应内容也是高考考查的热点.

例2A1,A2,A3,A4是椭圆b2x2+a2y2=a2b2上的四点,则直线A1A2与直线A3A4的斜率互为相反数(或都不存在)时点A1,A2,A3,A4共圆．

证明若直线直线A1A2与直线A3A4的斜率都不存在或都为零,由椭圆的对称性易知,四边形A1A2A3A4或为等腰梯形,或为矩形,两者都可得出对角互补,故点A1,A2,A3,A4共圆.

若直线A1A2与直线A3A4的斜率互为相反数且不为零,易得直线A1A2与直线A3A4相交.设其交点为P(x0,y0),则直线A1A2与直线A3A4的参数方程分别为

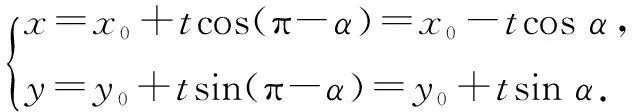
代入椭圆方程b2x2+a2y2=a2b2,整理得

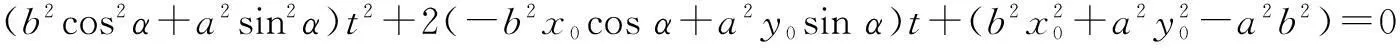
故得

PA1·PA2=|t1t2|

PA3·PA4=|t3t4|

所以PA1·PA2=PA3·PA4,

由割线定理的逆定理可知,点A1,A2,A3,A4共圆．

(1)求椭圆的标准方程;

(2)证明P,Q两点的横坐标的平方和为定值;

(3)过点A,P,Q的动圆记为圆C,动圆C过不同于A的定点,请求出该定点坐标.

通过以上两类问题的解决,可以发现直线参数方程为我们在高中阶段解决直线与圆锥曲线问题带来了无限的生机和广阔的解题空间；特别是与根与系数的关系结合在一起解决距离有关的问题,会使人感觉到耳目一新,起到意想不到的效果.