“抛物线及其标准方程”教学设计
2016-04-25闫瑞霞
“抛物线及其标准方程”教学设计
闫瑞霞
(山西省沁水县沁水中学,048200)
一、教材分析
1.教材前后联系,地位与作用
抛物线及其标准方程是普通高中课程标准实验教科书(人教版)选修2-1中的第二章第四节的内容.
学生已经学习了椭圆和双曲线的定义、方程和几何性质,对坐标法已有了初步的认识,这些为学习抛物线奠定了基础;同时,对抛物线的定义、方程的学习能让学生进一步深化对坐标法的认识,也为下一节用代数方法研究抛物线的几何性质做好铺垫.
抛物线在生产和科学技术中有广泛的应用,体现了数学与生产和科学技术的紧密联系,这就要求我们在教学中注意理论联系实际,培养学生应用数学的能力,学以致用.
2.教学目标
(1)知识与技能.掌握抛物线的定义,掌握抛物线的四种标准方程形式及其对应的焦点、准线.
(2) 过程与方法.掌握对抛物线标准方程的推导,进一步理解求曲线方程的方法——坐标法.通过本节课的学习,提高学生观察、类比、分析和概括的能力.
(3)情感、态度与价值观.通过本节的学习,体验研究解析几何的基本思想,感受圆锥曲线在刻画现实和解决实际问题中的作用,进一步体会数形结合的思想.
3.教学重难点
(1)重点.抛物线的定义及焦点、准线;抛物线的四种标准方程和p的几何意义.
(2)难点.在推导抛物线标准方程的过程中,如何选择适当的坐标系.
二、教法与学法
1.教法
本节课主要采用启发引导法.在整个教学过程中,引导学生观察、分析和归纳,使学生思维紧紧围绕“问题”层层展开,培养学生学习的兴趣,也充分体现以教师为主导,学生为主体的教学理念.同时,采用多媒体辅助教学,借助多媒体快捷、形象和生动的辅助作用,突出知识的形成过程,符合学生的认识规律,也可以增加趣味.
2.学法
本节课从引入课题开始,尽可能让学生参与知识的产生及形成过程,充分发挥学生的主体作用,使学生全方位地参与问题结论的得出,教师只起点拨作用.这样做不仅可以增加学生的参与机会,提高参与意识,而且教给了学生获取知识的途径,思考问题的方法,使学生真正成为教学的主体.
三、教学过程
1.创设情境,引入课题
用多媒体辅助教学向学生展示益智游戏《愤怒的小鸟》的视频.
设计意图用学生感兴趣的益智游戏引入课题,激发学生的学习兴趣,体会数学是源于生活又服务于生活.
2.学生自学,合作探究
探究1抛物线定义
阅读课本第64页~第67页,回答下列问题,开展探究活动:
用几何画板画图,如图1.点F是定点,l是不经过点F的定直线,H是l上任意一点,过点H作MH⊥l,线段FH的垂直平分线m交MH于点M,拖动点H,观察点M的轨迹.
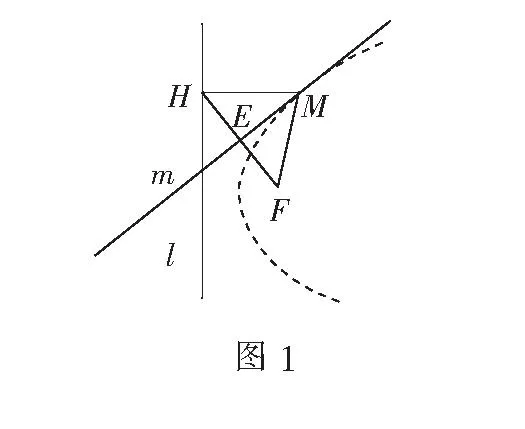
问题1点M的轨迹是什么?
问题2你能发现点M满足的几何条件吗?
问题3在抛物线定义中,条件“l不经过点F”去掉是否可以?
探究2抛物线的标准方程
问题4求曲线方程的一般步骤是什么?
问题5你认为如何选择坐标系,能使抛物线方程更简单?
问题6请你推导出抛物线的方程.
问题7标准方程y2=2px(p>0)中p的几何意义是什么?
问题8如果抛物线的开口方向向下,或向左(向右)时,其标准方程又是什么?并填写课本第66页表格.
设计意图让学生自主学习,合作探究,参与知识的产生及形成过程,充分发挥学生的主体作用,使学生全方位地参与问题结论的得出,教师只起到点拨作用.这样做不仅增加了学生的参与机会,提高了参与意识,而且教给了学生获取知识的途径、思考问题的方法,使学生真正成了教学的主体.
3.展示交流,精讲点拨
(1)教师用几何画板展示课本第64页中的数学实验.
(2)学生展示探究1,并给出抛物线的定义.
(3)定直线l不经过点F时,将会得到怎样的曲线?
训练1
(i)方程
表示的曲线是()
(A)圆(B)椭圆
(C)双曲线(D)抛物线
(ii)若动点P与定点F(1,1)和直线l:3x+y-4=0的距离相等,则动点P的轨迹是()
(A)椭圆(B)双曲线
(C)抛物线(D)直线
(4)学生展示探究2,并完成下表1:
注意应将图形的位置特征和方程的形式结合起来记忆,通过四种标准方程对比并总结:
① 方程的一次项决定焦点的位置,
② 一次项系数的符号决定开口方向.
训练2
(i)已知抛物线的方程如下,求其焦点坐标和准线方程:
①y2=-6x;
②3x2+5y=0.
(ii)分别求满足下列条件的抛物线的标准方程:
①准线方程为2y+4=0;
②焦点在直线x+3y+15=0上.
解题感悟:________________.
设计意图用几何画板完成数学实验,让学生在美观、动静结合中经历抛物线定义的形成过程.再由学生口述定义,如不完整,教师进行补充;并让学生注意到:直线l不经过定点F.
通过训练1加深学生对抛物线的定义的理解,由感性认识上升到理性认识.由学生展示建系方法,教师引导,总结出不同的方法.

让三个小组到黑板上,分别推导其中一种情况的抛物线的方程,并得出抛物线的标准方程,从而突破本节课的难点;并强调p的几何意义,突出本节课的重点.
再让三个小组到黑板上,分别推导开口向左(上、下)的抛物线标准方程.
填表后,教师引导学生结合抛物线的位置特征和方程形式进行记忆,使学生更好地掌握本节的重点内容.
通过训练2,巩固四种方程形式及曲线特征,引导学生代数与几何的互化,渗透数形结合的思想,强化解析几何的基本思想与方法.
4.课堂小结,拓展训练
(1)课堂小结
①今天学到了什么?(知识方面)
②体验了哪些数学思想?
(2)拓展训练
①求抛物线y=ax2(a≠0)的焦点坐标和准线方程;
②求经过过点(3,-4)的抛物线的标准方程.
(3)布置作业
必做题:课本第73页A组1,3,4.
选做题:
(i)抛物线y=4x2上的一点M到焦点的距离为1,则点M的纵坐标是 ()
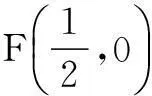
①求点M的轨迹方程;
②是否存在M,使|MA|+|MF|取得最小值?若存在,求此时点M的坐标;若不存在,请说明理由.
设计意图课堂小结,拓展训练,是学生对本节课内容的一个总结与提升,培养学生的归纳与总结能力,同时又是对本节课所学知识的一个检验,也加深了学生对本节知识的理解和记忆.作业的安排是为了巩固所学知识,提高学生对知识的运用能力.分为必做题和选做题,这样,可以让不同层次的学生得到不同的发展.
