精心设计 以问导学



精心设计以问导学

林赠英

(福建省武平县第一中学，364300)

为了有助于“先学后教,以学定教”的有效进行,教师可以引导学生自觉学习、独立思考、相互合作.“以问导学”能较好地激发学生学习热情,控制学生学习过程,开动学生脑筋,因此,要精心设计好的问题帮助学生预学.笔者认为要达到这一目标教师可以从以下几个方面进行设计:

一、设问于学生的“最近发展区”

学生已有的知识、生活经验、基本技能是预学的基础.预学应从学生实际出发,根据学生的知识水平、接受能力和心理特点,寻找新旧知识的联系,找出新知识的生长点,发现学生的“最近发展区”,设计出能启发学生思考、诱导学生学习的问题来,促进学生不断把最近发展区转化为现有发展水平,把最近发展区不断推进,从而学会新的知识和技能．例如,学习“一元二次不等式的解法”, 二次函数的概念、图象、一元二次方程的根和解法是知识的生长点,二次函数、一元二次方程、一元二次不等式的关系是学生的最近发展区.可以设计以下问题引导学生预学,从中发现一元二次不等式的解集与一元二次方程的根、二次函数图象的关系,探究一元二次不等式的解法与一元二次方程解法的联系,最终得到一元二次不等式的解法．

问题1画下列函数的图象:

(1)y=x2+2x-3；

(2)y=x2+2x+1；

(3)y=x2+2x+2.

问题2就上面三个函数回答下列问题：

(1) 当x取什么值时,y=0？

(2) 当x取什么值时,y>0？

(3) 当x取什么值时,y<0？

问题3“当x取什么值时,y>0”这一问题可以用什么式子表示?

问题4如何求不等式x2+2x-3>0的解集?与解方程x2+2x-3=0有什么异同?

问题5归纳总结一元二次不等式的解法．

二、设问于学生的模糊易混处

在预学过程中,难免会碰到模糊易混的内容,教师要针对模糊点、易混处精心设计问题,通过思考,变迷茫为清楚,使学生有一种“洞然若开”,“豁然开朗”的感觉．例如,学生对棱柱概念中的“其余各面都是四边形,并且每相邻两个四边形的公共边都互相平行”模糊不清,可设计下面的问题帮助学生弄清棱柱的概念．

问题1下面两句话含义相同吗?能用第二句作为棱柱的定义吗?

第一句:有两个面互相平行,其余各面都是四边形,并且每相邻两个四边形的公共边都互相平行,由这些面所围成的多面体叫做棱柱．

第二句:有两个面互相平行,其余各面都是平行四边形的多面体是棱柱．

问题2图1中的两个图形符合哪一句话,它们是棱柱吗?

三、设问于学生的易错处

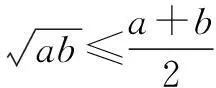
问题下列各函数中,最小值为2的为______．

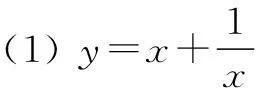
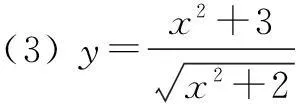
四、设问于学生的疑难处

问题1计算(2x-3)(x2+x-1),多项式乘以多项式的法则如何?

问题2乘方的意义是什么?(a+b)n有多少个什么相乘?(a+b)n如何乘?

问题3根据多项式乘以多项式的法则,如何从每个括号中取数相乘?若每个括号都取a相乘,怎么表示?有一个括号不取a,该括号必取b吗?有一个括号不取a有几种取法?以此类推,两个、三个…n个括号不取a,如何取数相乘?是否有规律?

学生想清楚这些问题以后,就能更好地理解二项式定理并证之．

五、设问于学生的盲区

学生对问题的拓展、变式，从不同角度提出问题分析问题等能力不高,需要教师扶上马,送一程,才能提高学生学习数学的能力,更好地锻炼学生的思维．例如,人教A版必修5第7页例3:在∆ABC中,已知b=60 cm,c=34 cm,A=41°,解三角形(角度精确到1°,边长精确到1cm)．用余弦定理求出a后,可设问:求角C用正弦定理好,还是用余弦定理好?角B、角C哪个先求好?为什么?用什么方法求更简单?通过思考和比较,学生懂得了若用余弦定理,先求谁都一样．若用正弦定理,先求哪个却有优劣之分,因为由角的正弦值看不出它是锐角还是钝角,先求大角的话必须讨论,增加麻烦,所以用正弦定理宜先求较小的角．这里，用余弦定理计算量较大,用正弦定理计算量较小.综合以上分析,学生明白了该题为什么要用正弦定理先求较小的角C．若没有对这些问题的思考,学生就不知道解三角形还需考虑这些问题.通过探究活动,不但使学生掌握了解三角形的方法、技巧,还提高了学生分析问题、解决问题的能力．

呈现给学生有价值的问题让学生去探索、去解决,学生的学习活动不再盲目,不再被动,预学更顺利；教更有针对性,学生学习数学的能力和数学素养就有望更快提高．