高耦合度电感储能型脉冲功率源仿真分析

张　超*,董健年,张　军（南京理工大学　能源与动力工程学院,南京　210094）



高耦合度电感储能型脉冲功率源仿真分析

张超*,董健年,张军
（南京理工大学能源与动力工程学院,南京210094）

摘 要：为了研究高耦合度电感储能型脉冲功率源，本文首先仿真了STRETCH Meat grinder电路，通过得到的电流电压波形分析了该电路的工作过程；然后再利用有限元方法来分析该拓扑中耦合电感的磁场特性。通过建立耦合电感线圈的二维仿真模型得到了磁场能量分布云图、磁感应强度分布云图以及磁感应强度矢量图和电磁力矢量图，得出耦合电感的磁场分布规律以及电感的受力趋势。为了进一步直观的研究耦合电感的受力，本文还仿真计算了在垂直方向上电感的受力情况。为高耦合度电感储能型脉冲功率源优化设计提供了一定的理论依据。

关键词：STRETCH Meat grinder；脉冲功率源；耦合电感；有限元分析；磁场

1　引言

在电磁发射技术中，为满足作战的需求，电源小型化显得尤为重要[1]。相比较而言，电感储能型脉冲功率源以其储能密度高、传输功率大、结构紧凑、体积小、成本低等优点[2]成为了研究的热点。

对于电感储能型脉冲功率源的研究，美国IAT通过对传统的Meat grinder电路进行改进提出了STRETCH Meat grinder拓扑[3-4]，该拓扑引入耦合电感，利用磁通压缩的原理，通过互感实现电流倍增，大大提高了带负载的能力[5]。STRETCH Meat grinder电路中为了提高能量的传输效率，耦合电感的优化设计是关键，以前的研究主要集中在提高两电感的耦合度上，如今耦合度已提高到0.9以上，在高耦合度情况下强磁场的影响将会凸显出来，基于此本文在仿真分析拓扑结构的背景下以其高耦合度电感为模型，利用有限元方法分析了其磁场特性以及耦合电感线圈受力情况。

2　STRETCH Meat grinder拓扑仿真分析

STRETCH Meat grinder仿真电路如图1所示，初级电源的充电电压为6kV,电感L1=1249μH,L2=321.5μH(耦合系数0.974),脉冲电容C1=105.2mF,放电电阻R2=100KΩ,等效负载中电感L3=1.4Μh,电阻R1=0.5mΩ；仿真电压电流波形如图2、图3所示。

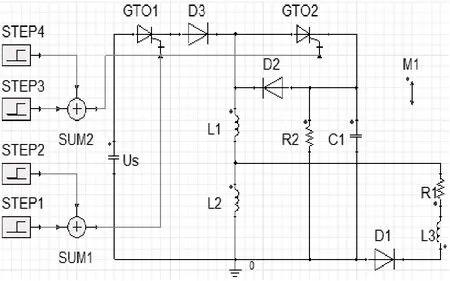
图1　STRETCH Meat grinder仿真电路

图2　STRETCH Meat grinder电压仿真

图3　STRETCH Meat grinder电流仿真波形

根据STRETCH Meat grinder电压电流波形图并结合开关器件的触发时间引起的电路工作状态的变换可将拓扑的工作过程划分为五个阶段。

第一阶段：闭合开关Sop(IGCT，仿真过程中是用GTO替代)，让初级电源Us给电感L1、L2充电，电流增加到满足要求的值时关断全控器件Sop，进入第二个阶段。（7.55ms以前）

第二阶段：当Sop关断后，电感L1中的磁通都会迅速的减小，由于L1、L2间耦合连接磁链守恒，所以L1中的电流和磁通就会快速增加，并通过二极管D1给负载供电；L1、L2不可能理想耦合，必然有漏磁通的存在，为防止击穿主管，拓扑中加入了脉冲电容C，漏磁通产生的电流将对其充电。（7.55-7.7ms）

第三个阶段：晶闸管GTO2没有导通，电容上的电压将保持不变，仅由电感L2给负载供电。(7.7-8.25ms)

第四阶段：触发晶闸管GTO2，C1释放在第二阶段储存的L1的漏感能量给负载，此过程中可等效的看着是两个电感同时给负载供电，负载电流将达到一个峰值直到电感L1中的电流再次降为0。(8.25-8.8ms)

第五阶段：只有L2给负载供电，然后电容上的电压保持负值不变。只要合理的控制触发晶闸管GTO2的时序，是能够很好的使先前储存的电容中的能量得以利用的。(8.8ms以后)

从以上电路工作状态可以看出，第二阶段是关键，脉冲功率源的实质就是将初级能源进行压缩储存然后再以脉冲的形式传给负载，在本拓扑中此功能就靠两耦合电感通过磁通压缩的原理将能量传给负载。在设计中让L1是L2的几十倍，这样电感L2中的电流就会急剧上升，将两电感大部分的能量都加到负载，传递到负载的能量大小就取决于两电感的耦合程度，在分析计算中电感间的耦合程度可以用耦合系数K来表示。

从这个式子可以看出，要想提高耦合度，就得增大两电感间的互感M，M的大小与两线圈的形状、匝数、磁介质的种类及它们的相对位置有关[6]。空间两个圆线圈可由r0，d0,α三个量来确定其位置关系，由此建立单匝线圈之间的互感计算模型如图4所示。

得到线圈间的互感计算公式为[7]：

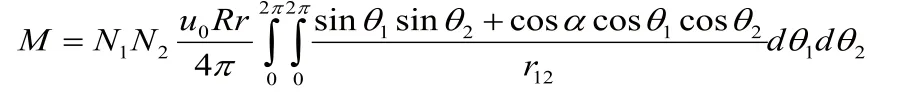
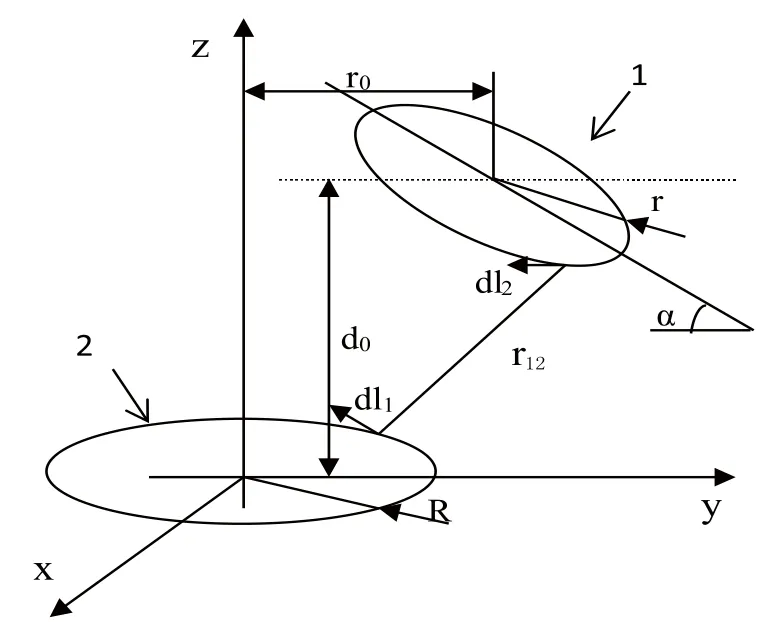
图4　两电感线圈互感计算模型

式中R、r为两线圈的半径，N1、N2为两电感的匝数，r12为两线圈上电流元间的矢径，α为线圈1与y轴夹角，显然，当α为0时尽量缩小r12可以得到较大的互感，从而得到较高的耦合度，利用这种原理得到的高耦合电感。

3　耦合电感磁场有限元分析

3.1仿真模型的建立

本文的仿真结构采用L1、L2交互相隔的方法来保证耦合系数，先对两电感进行小单元分组，然后各组之间依次间隔排列，最后再在各层之间填充环氧树脂来保证绝缘。采用的材料为铜片，最小单元有两类，一类厚度为4mm,一类厚度为8mm，其匝间间隙都为1.2mm,电感L1为1249uH，被分为7组，由13个第一类单元串联组成，其中有6组是由两个第一类单元叠加串联而成；电感L2为321.5uH，分为6组，由6个第二类单元串联而成，最终的耦合电感就由L1的7组电感与L2的6组电感交互相隔叠在一起构成。在对称坐标系RZ平面下建立耦合电感的磁场分布仿真模型，如图5所示。

图5　耦合电感的仿真模型

图5(a)中每个小矩形代表每匝线圈，每一排小矩形代表每一层线圈，相对较矮的矩形代表电感L1的部分，相对较高的代表L2的部分。大的矩形部分代表求解区域。仿真中的加载电流如图3，从图中可以看出，在0到7.55毫秒内的电流为线性变化，而7.55毫秒以后为非线性变化，因此在加载耦合电感电流的时候，可以分为这两个过程进行加载。

3.2 仿真结果分析

通过以上的仿真，得到的结果如图6、图7、图8、图9所示。

图6　磁场能量分布云图 　

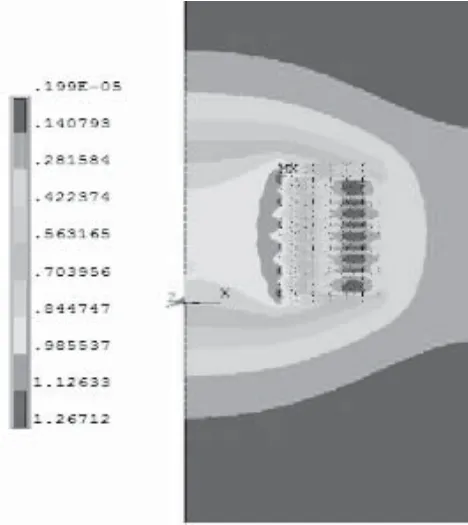
图7　磁感应强度分布云图

图8　磁感应强度矢量图　

图9　电磁力矢量图

从图6可以看出耦合电感的能量主要分布在靠近电感的内外侧，能量的最大值在耦合电感内部中心处，从电感端部的能量密度来看，磁场对外有漏磁存在；从图7可以看出磁场的最大值为1.267T，最大磁场处在电感L2的内侧，在实际中L2中的电流是L1的几十倍且电流是从L2的内侧流入的，说明仿真与实际相符。从图8中的磁场方向可以大致判断电感将受到一个径向向外的电磁力，图9刚好验证了这一点，从电磁力矢量图可以清晰的看出耦合电感将受到一个向外侧中心挤压的力，仿真数据显示所受力最大处为149.695N，最大力主要出现在第二层和第十七层线圈处。

为了进一步具体的研究线圈受力情况，在仿真的过程中也求解了每层线圈在垂直方向上受力的情况，如图10所示，横坐标为每层线圈的编号，编号如图5（b）所示，纵坐标为每层线圈在纵轴方向所受的力。

图10　每层线圈的受力

从图中可以看出在1-9层线圈受力的方向为纵轴正方形，而11-19层线圈受力为纵轴的负方向，因此线圈将会有向中间收拢的趋势，同时也可以从图中看出中间层的线圈受力较小，上下层的线圈受力较大，其中第二层线圈受力最大，为49.47kN，所以在实际制作耦合电感的过程中必须对两端加强固定。

4　结论

本文通过对电感储能型脉冲功率源的仿真分析可以得出如下结论：

（1）从STRETCH Meat grinder仿真电压电流波形可以看出电感L1的能量能够通过耦合高效率的传给电感L2继而传给负载，就算有漏磁的存在，由于脉冲电容的加入，迫使这部分能量再次传递到负载而被利用。

（2）耦合电感储能密度较高，储存的能量主要集中在耦合电感的内外靠近电感处，且最大能量值出现在耦合电感的中心处。

（3）耦合电感中的磁场强度较大，最大值出现在电感L2的内侧。

（4）耦合电感在通电后将会受到一个向外部中心处挤压的力；在构成耦合电感的所有线圈层中在垂直方向上受力较大，电感线圈会有向中间收拢的趋势。

参考文献：

[1]李军,严萍,袁伟群.电磁轨道跑发射技术的发展与现状[J].高电压技术，2014,40(04):1052-1064.

Li Jun,Yan Ping,Yuan Weiqun.Electromagnetic gun technology and its development[J].High Voltage Engineering,2014,40(4):1052-1064(in Chinese)

[2]王莹.高功率脉冲电源[M].北京:原子能出版社,1991.

[3]Lindner K，Long J，Girogi D，et a1．A Meat grinder circuit for energizing resistive and varying inductive loads(Em Guns)[J]．IEEE Transactions on Magnetics,1986，22(6)：1591-1596．

[4]Sitzman A，Surls D，Mallick J．Design，construction，and testing of an inductive pulsed—power supply for a small railgun[J]．IEEE Transactions on Magnetics，2007，43(1)：270-274．

[5]初祥祥,于歆杰,刘秀成.三种电感储能型脉冲功率源电气性能的比较[J].电工电能新技术,2012,31(03):20-24.

[6]王素娇.磁耦合线圈互感系数M的测量[J].郑州铁路职业技术学院学报，2OO2,14(14):43-44.

[7]殷莉.仿真人体环境中RF MEMS电感耦合特性实验研究[D].北京：北京交通大学,2010.

*为通讯作者

作者简介：张超（1989-），男，研究生，研究方向：高耦合度电感储能型脉冲功率源的研究。

DOI:10.16640/j.cnki.37-1222/t.2016.03.044