对一道同步卫星变轨题的评析

陈小明

(铜陵市第一中学　安徽 铜陵　244000)



对一道同步卫星变轨题的评析

陈小明

(铜陵市第一中学安徽 铜陵244000)

摘 要：以2015年高考新课标Ⅱ卷第16题为例，分析了发射场不在赤道的同步卫星的变轨过程，并对题中的难点作了进一步讨论.

关键词：同步卫星变轨非赤道发射

卫星变轨是高中物理天体运动中的常见问题，也是学生学习中的一处难点.2015年高考新课标Ⅱ卷第16题，重点考查了同步卫星的变轨运动，试题将学生常见的同一平面内变轨拓展为不同平面内的变轨，涉及到矢量运算、空间构图等，对学生的多方面能力进行了有效检测.下文笔者将结合平时的教学，对同步卫星发射中的变轨问题进行分析，同时对赤道上和非赤道上发射进行比较，帮助学生正确理解卫星的变轨过程.

1模型分析

1.1发射场在赤道

发射同步卫星的运载火箭一般为三级，先来分析发射时的简化模型(图1).

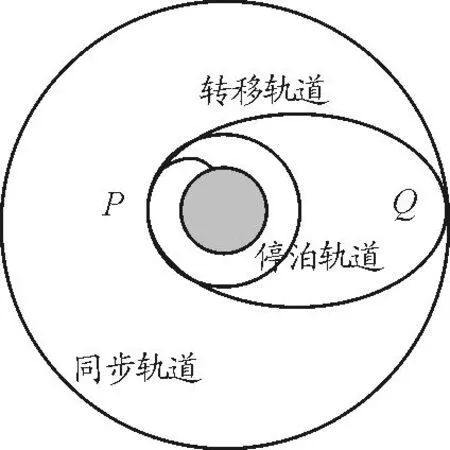
图1

运载火箭的第一级和第二级依次启动，使火箭垂直向上加速，到第二级火箭脱离后转弯进入一个高度较低的圆形轨道，称为停泊轨道，一般为几百千米.在停泊轨道上运行少许时间，卫星快要到达与转移轨道交点时，第三级火箭点火，使卫星进入一个椭圆形的转移轨道.之后在转移轨道上运行几圈，完成姿态调整和远地点点火前准备工作，当卫星到达远地点，启动卫星上的远地点发动机，改变卫星的速度，使之进入同步轨道.此处的转移轨道由德国工程师奥尔特·霍曼于1925年首先提出，又称霍曼轨道.

转移轨道上近地点P和远地点Q的速率可求解如下，估算时，忽略停泊轨道的高度，设同步轨道高度h=36 000 km，地球半径R=6 370 km，地球质量M=5.98×1024kg，卫星质量为m，卫星从P点运动到Q点，由机械能守恒定律可得

由角动量守恒定律可得

mRvP=m(R+h)vQ

联立两式解得

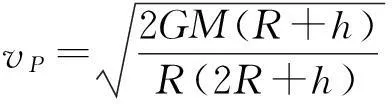
1.2发射场不在赤道

运载火箭的第一、二级启动与在赤道上的过程一样，而其停泊轨道为与赤道平面有一定夹角的倾斜圆形轨道，以地球球心为圆心，卫星快要到达停泊轨道与赤道平面交点时，点燃第三级火箭使卫星进入椭圆转移轨道，椭圆轨道与停泊轨道共面，椭圆轨道与赤道平面夹角因发射地点不同而不同.其近地点为停泊轨道与赤道平面交点，远地点为转移轨道与赤道平面的另一个交点，近地点和远地点都在赤道平面内.当卫星到达远地点时，启动远地点发动机，改变速度的大小和方向，并对卫星进行姿态调整，进入同步轨道.

2原题再现

【题目】(2015年高考新课标Ⅱ卷第16题)由于卫星的发射场不在赤道上，同步卫星发射后需要从转移轨道经过调整再进入地球同步轨道.当卫星在转移轨道上飞经赤道上空时，发动机点火，给卫星一附加速度，使卫星沿同步轨道运行.已知同步卫星的环绕速度约为3.1×103m/s，某次发射卫星飞经赤道上空时的速度为1.55×103m/s，此时卫星的高度与同步轨道的高度相同，转移轨道和同步轨道的夹角为30°，如图2所示，发动机给卫星的附加速度的方向和大小约为

A.西偏北方向，1.9×103m/s

B.东偏南方向，1.9×103m/s

C.西偏北方向，2.7×103m/s

D.东偏南方向，2.7×103m/s

图2

解析：本题为非赤道上发射同步卫星，由前面非赤道发射过程的分析可知，本题所考查为从转移轨道的远地点到同步轨道的速度调整情况.可将过程绘制成图3.

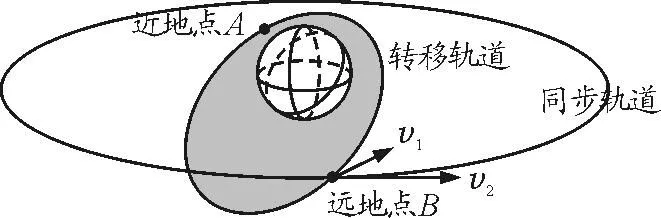
图3

其中停泊轨道未画出，灰色部分为椭圆转移轨道，地球球心为其一个焦点.近地点A在赤道平面内，椭圆转移轨道平面与同步卫星轨道平面成30°，故椭圆轨道在B的速度v1与同步轨道在B的速度v2成30°，在B点由速度的矢量分析图4可知，附加速度Δv为v2与v1的矢量差，由余弦定理得

v1和v2的方向为图2中两个箭头的方向，将图4结合图2所示的方向，可知附加速度东偏南方向.

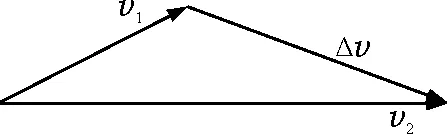
图4

3评价反思

本题以同步卫星的发射为背景，考查卫星从转移轨道的远地点进入同步轨道的情况.学生在高中的学习过程中，会遇到很多类似的习题，但都是停泊轨道、转移轨道和同步轨道在一个平面上的情况，这些问题可以通过离心运动进行定性的分析.而本题转移轨道与同步轨道有个夹角，需要进行定量计算，要求学生在有限的时间内，从速度的矢量变化求出附加速度，有一定的难度，并且题中有两处情景增加了试题的分析难度.

首先，题中所涉及为转移轨道至同步轨道，此过程的图像即使同一平面内，让一般学生画出尚且有困难.现题中给出为两平面互成角度，因此更不容易画出来.笔者曾与其他教师讨论过此图，都认为该图容易误解.图中画出的大圆，很容易看成同步轨道，这样就会误认为俯视图.而实际题中为正视图，大圆可理解成地球的边缘线.图中实线、虚线和箭头的含义也容易看错，致使题中所标注的赤道、转移轨道和同步轨道在不了解的情况下，找不到实际的位置，起不到助于理解的作用.

其次，学生平时遇到的同平面变轨，能从图中清楚看出是在远地点变轨，而现在非同平面，理论上只要两个轨道有交点都可以变轨，但学生无法确切地知道这次的变轨也是在远地点进行，如果此次不在远地点变轨，那么变轨前后两个速度的夹角就不是30°，也就无法求解.

试题以非赤道同步卫星的发射为背景，也启发了我们在平时教学中，不能只停留在遇到的题目层面上，要善于对问题进行适当的拓展，举一反三，适当介绍一些前沿的知识，开阔学生的眼界和思维.

(收稿日期：2015-11-08)