均匀杆在什么位置离开竖直墙面

姜付锦

(武汉市黄陂一中　湖北 武汉　430300)



均匀杆在什么位置离开竖直墙面

姜付锦

(武汉市黄陂一中湖北 武汉430300)

摘 要：先以杆的质心C为研究对象并结合机械能守恒定律求出杆转动的角速度与夹角θ的关系，接着用牛顿第二定律分析了匀质杆脱离墙面的条件，最后求得匀质杆脱离墙面的角度.通过研究发现,这个角与杆的长度无关，理论上有4个解,其中有两个虚数解,一个解为零，还有一个实数解；当两个小球质量相同时脱离角度为.

关键词：转动惯量机械能守恒定律脱离条件

1题目

如图1所示，小球A和B的质量分别为m1,m2，两球之间用一长为L，质量为m均匀分布的杆连接，杆放在光滑的水平面和光滑的竖直墙壁之间.开始时杆与竖直墙面的夹角为θ0，某一时刻释放杆，试分析当小球A脱离墙壁时杆与墙壁的夹角.

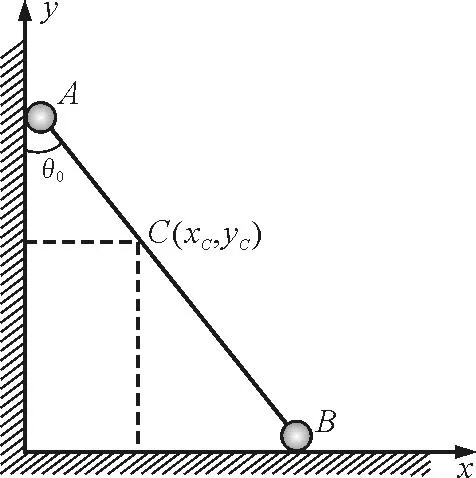
图1

2杆转动角速度的求解

某一时刻杆与墙壁成θ角，则系统的质心位置坐标为(xC,yC)，由质心的定义式可知

整理后得

对位置坐标求时间t的一阶导数得质心的两个分速度大小

对位置坐标求时间t的二阶导数得质心的两个分加速大小

由系统机械能守恒可知

式中JC=aL2(a为某一定值)为系统相对于质心的转动惯量，则得

g{L[4(m2-m1)(m1+m2+m)cos2θ+

(m+2m1)2+4(m1+m2+m)a]}-1

两边对时间求导得

(m+2m1)2+4(m1+m2+m)a]2}-1

进一步整理得

m1)(m1+m2+m)cos2θ+8(m2-m1)(m1+m2+

m)cosθ0cosθ+(m+2m1)2+4(m1+m2+

m)a]{L[4(m2-m1)(m1+m2+m)cos2θ+

(m+2m1)2+4(m1+m2+m)a]2}-1

3系统的转动惯量的计算[1]

系统对过质心垂直纸面的轴的转动惯量为

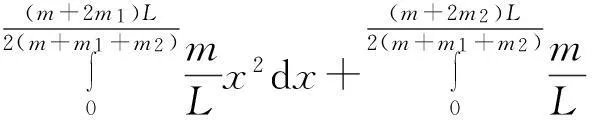
整理后得

4小球A脱离墙面的条件

如图2所示，系统所受的外力有重力、地面支持力和墙面的弹力，墙面的弹力的方向水平向右.

图2　系统的受力图

FB-(m1+m2+m)g

当FA=0时，小球A脱离墙面，则有

代数值后整理得

{4(m2-m1)(m1+m2+m)cos3θ+

3[(m+2m1)2+4(m1+m2+m)a]cosθ-

2[(m+2m1)2+4(m1+m2+m)a]cosθ0}·sinθ=0

式中

5杆与墙壁夹角的求解

这个方程有一个特解sinθ=0，即θ=0，由题意可知这个解无意义舍去.

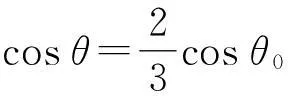
(2)当m1≠m2时，cosθ在理论上有3个解，其中有两个解是虚数，另外1个实数解，由于这个方程非常复杂，很难求出解析解，故本文给出以下数值模拟解：

设m1=2 kg,m2=4 kg,m=1 kg,初始角度为θ0，则脱离时的角度满足

cosθ=

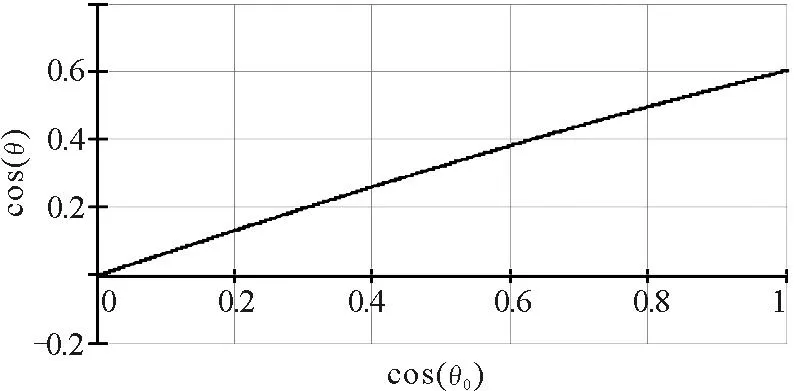
图3　当系统质量一定时，脱离角度与初始角度的关系

由图3可知，初始时角度的cos(θ0)越大，脱离时角度的cos(θ)越大；当θ0=0时，cos(θ)=0.604，约为52.8°.若系统质量是其他值时，则只需将以上的程序略作修改即可，限于篇幅这里不再讨论.

参 考 文 献

1周衍柏.理论力学教程(第2版). 北京：高等教育出版社,1985.128~131

2郑永令,贾起民.普通物理学教程丛书 力学(第1版).上海：复旦大学出版社，1989.280~282

(收稿日期：2015-10-29)