高中物理竞赛中复杂直流电路的分析方法——以一道2015年全国物理竞赛题为例



高中物理竞赛中复杂直流电路的分析方法
——以一道2015年全国物理竞赛题为例

陈玉奇

(江苏省姜堰中等专业学校江苏 泰州225500)

复杂直流电路属于大学电学部分的知识，能力要求较高，在高考中不作要求，但在物理竞赛中，却是考纲规定的考试内容.历年的许多省市乃至全国的物理竞赛中，时常出现复杂直流电路的问题，学生普遍感到比较困难，不知道如何下手，甚至使问题变得更加复杂.因此，要想在竞赛中快速而准确地解决此类问题，必须要求学生对复杂直流电路的相关知识有更深层次的理解和掌握.

1什么是复杂直流电路

高中阶段所接触的电路一般是由电阻组成的混联电路，对于这种电路的计算，学生只需根据电阻串、并联规律把电路尽量化简，逐步求解即可.有些貌似复杂的电路在使用串、并联公式后变为一个无分支的闭合电路，问题就可迎刃而解，我们把这种电路称为简单直流电路.但对于某些电路，用这种方法则无法化简，比如图1中的电桥电路，尽管其结构简单，但我们却无法指出各个电阻之间的串并联关系.另外，如果电路中有两个以上的含电源支路，也会出现同样的问题.这种不能运用电阻串、并联的计算方法将其简化成一个单回路的电路，我们把它称为复杂直流电路.

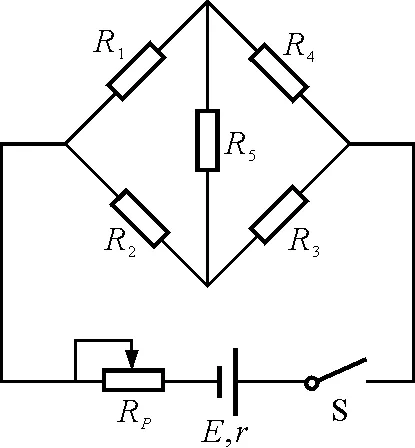
图1

2解决复杂直流电路的基本依据

复杂直流电路与简单直流电路的区别并非是电路结构的繁与简，而是体现在处理两种电路的方法上.分析复杂直流电路的基本依据是基尔霍夫定律，该定律包含两个方面的内容.

(1)基尔霍夫第一定律，又称节点电流定律(KCL).它指出：电路中任意一个节点上，在任一时刻，流入节点电流之和等于流出节点电流之和，即

∑I入=∑I出

KCL是电路中各支路在节点(或封闭面)处必须满足的电流约束关系，与电路中各支路元件的性质无关，是电荷守恒的必然结果.

(2)基尔霍夫第二定律，又称回路电压定律(KVL).它指出：在一个回路中，从一点出发绕回路一周回到该点时，各段电压降的代数和等于零，即

∑U=0

KVL是电路的各回路中必须满足的电压约束关系，与回路中各元件的性质无关，是能量守恒的必然结果.

基尔霍夫定律是电路的基本定律之一，不论在何种电路中，它阐明的各支路电流之间和回路电压之间的基本关系都是普遍适用的.理论上来讲，基尔霍夫定律可以解决一切电路问题，它思路简单清晰，对于基础好的学生来讲，是完全可以做到熟练掌握和灵活应用的.但是不足之处在于，如果支路较多，所列方程的个数也会随之增多，从而使得解题过程比较繁琐.

3复杂直流电路的分析方法

下面以2015年第32届全国中学生物理竞赛复赛的第5题为例，通过对该题呈现出来的电路进行剖析，谈谈复杂直流电路的分析方法.

【题目】如图2所示，“田”字形导线框置于光滑水平面上，其中每个小正方格每条边的长度l和电阻R分别为0.10 m和1.0 Ω.导线框处于磁感应强度B=1.0 T的均匀磁场中，磁场方向竖直向下，边界(如图2中虚线所示)与de边平行.今将导线框从磁场中匀速拉出，拉出速度的大小v=2.0 m/s，方向与de边垂直，与ae边平行.试求将导线框整体从磁场中拉出的过程中外力所做的功.

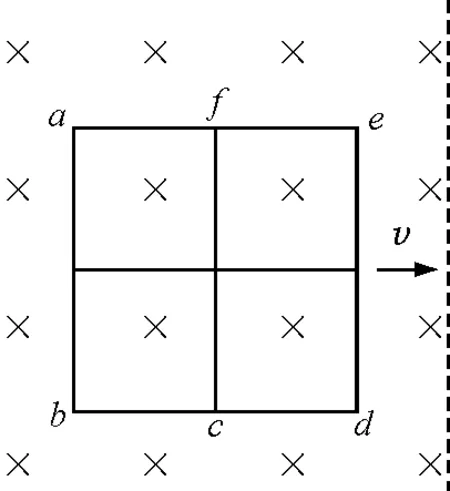
图2

分析：本题是一道电磁感应和直流电路相结合的综合题，其物理情景和物理过程并不是很复杂，考生只需根据题中所描述的物理过程，分别作出ed一条边拉出磁场和ed,fc两条边都拉出磁场的过程中所对应的两种等效电路，如图3和图4所示，求出两种情况下处于磁场中的几条边的电流及其所受的安培力.再由平衡条件求出两种情况下的外力，进而计算出将导体框整体拉出磁场的过程中外力所做的功.

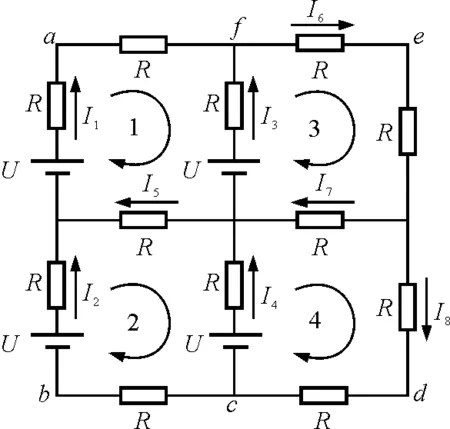
图3

由上可知，解决本题的关键步骤是正确求出上述两种情况下各相关支路的电流大小和方向.观察图3和图4可知这是两个复杂直流电路.限于篇幅，以下仅对图3所示的电路进行分析，图4的求解方法相同.本题其余部分的分析过程可参阅《2015年第32届全国中学生物理竞赛复赛理论考试试题及解答》，在此不再重复.

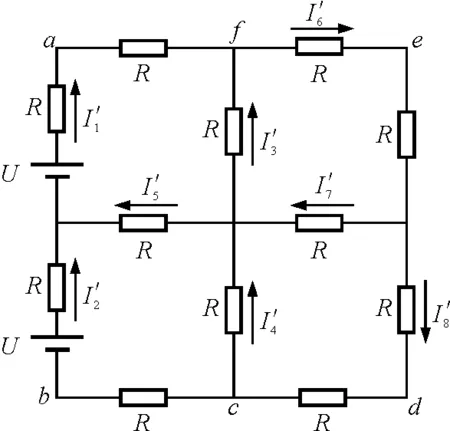
图4

3.1支路电流法

以支路电流为未知量，应用基尔霍夫定律，列出与支路电流数量相等的独立方程式，然后联立求解各支路电流的方法叫支路电流法.

对于图3，按图中所示的电流方向，根据基尔霍夫第一定律可得

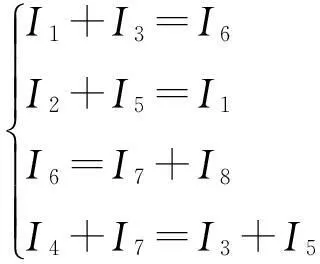
由基尔霍夫第二定律，对图3中的4个回路可列出电压方程

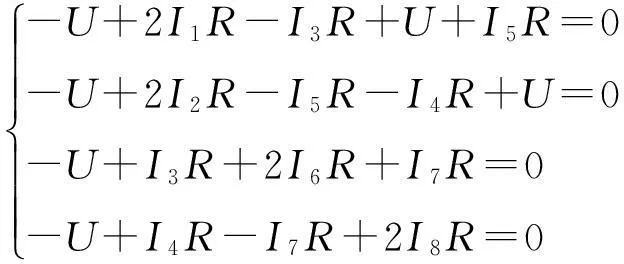
式中感应电动势为

U=Blv=0.2 V

(9)

联立式(1)～(9)，求得

I1=I2=0.025 A

I3=I4=0.05 A

点评:应用基尔霍夫定律时，可以任意假定电流的参考方向和回路的绕行方向.当求出的电流为正时，说明实际电流方向与所设的参考方向一致；当求出的电流为负时，说明实际电流方向与所设的参考方向相反.

对于有m条支路，n个节点的电路，依据第一定律只能列n-1个独立的电流方程，其余的m-(n-1)个方程只能根据第二定律列回路电压方程.所谓方程“独立”，即从数学上来讲，相互独立的方程中，任何一个方程都无法用其他几个方程推导出来，相互独立的n个方程可以解出n个未知数.本题中有8条支路，5个节点，只能列4个独立的电流方程，剩下的4个方程式，则由第二定律所列的电压方程来补足.

在列回路电压方程时，应注意两个问题：一是电压符号的选取，回路电压定律指出“各段电压降的代数和等于零”，因此，如果遇到电势升的情况，电压要取负号；二是回路的选取要使得所列的电压方程独立.图3中回路的个数有13个，而未知量只有8个，单纯从数量上来讲，仅仅依靠回路就可列出13个方程来，无需再依靠节点电流方程.但这13个电压方程中只有4个是独立的，有的方程可以由其他电压方程推导出来.例如本题中式(8)若选取图3左边的“日”字形回路来列，则式(8)就变为

-U+2I1R-I3R+U-I4R+U+2I2R-U=0

很显然该式可以由式(5)和(6)相加得到，用该式与式(5)、(6)、(7)联立是无法求解的，因而它不是独立的方程.在下面的讨论中我们就会发现，用网孔列出的回路电压方程都是独立的.

3.2网孔电流法

网孔是指中间没有支路穿过的回路，在图3所示的电路中，回路有13个，而网孔只有4个.

根据电流的连续性，可以假定一个电流在指定的网孔中流动，这种电流称为网孔电流.对于电路中每一个节点，网孔电流流入一次又流出一次，基尔霍夫第一定律自动满足.如果以网孔电流为未知数，只需应用基尔霍夫第二定律列出各网孔的回路电压方程，联立解出网孔电流，各支路电流则为相关网孔电流的代数和.

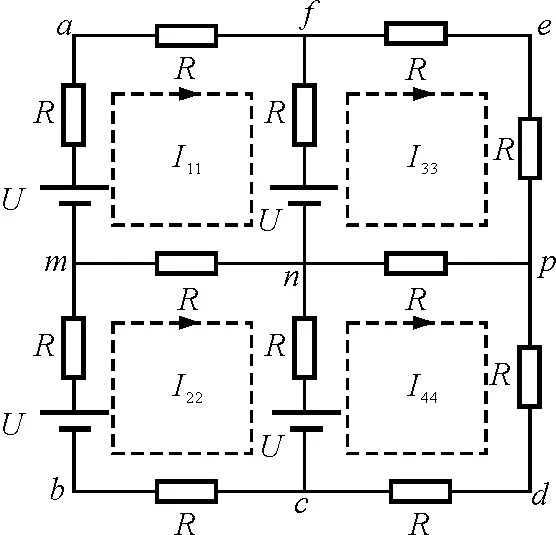
图5

设图5中的4个网孔电流分别为I11，I22，I33和I44，方向为顺时针，将其余3个节点设为m，n，p.注意到支路fn，mn，np，nc为相邻网孔的公共支路，每条支路均有两个网孔电流同时流过.

用基尔霍夫第二定律对4个网孔列电压方程

整理后代入数据，很容易求得

I11=I22=0.025 A

I33=I44=0.075 A

对比图5中的网孔电流和图3中各支路电流的对应关系，不难发现，fam和mbc为独立支路，每条支路只有一个网孔电流流过，故这两个支路中的实际电流就等于网孔电流，即I1=I11=0.025 A，I2=I22=0.025 A.fn,nc为公共支路，其实际电流应为相邻网孔电流的代数和，即

I3=I33-I11=0.05 A

I4=I44-I22=0.05 A

点评:网孔电流法和支路电流法相比，能有效减少解题时方程的个数，便于分析和求解.在列回路电压方程和利用网孔电流表示各支路电流的过程中，一定要分清独立支路和公共支路中的电流与网孔电流的关系，在上述解法中已经专门强调了这一点.对于电源，因所列回路电压方程只需考虑元件上电压的大小和方向，无论电源在哪种形式的支路中，两端的电压均不受网孔电流的影响.

我们还可以发现，对于一个复杂直流电路，求解电路所需的独立方程的个数与电路的网孔数相等.换句话说，电路中有几个网孔，我们就设几个独立变量.因而在本题中，即使我们用支路电流法求解，也只需设4个独立变量，譬如I1,I2,I3,I4，由基尔霍夫第一定律用这4个变量将其余4条支路的电流表示出来，而没有必要设出8个变量.具体到列电压方程时，可以直接选取网孔这样特殊的回路来列方程，且列出的方程式都是独立的，其余回路可以用来检验结果的正确与否.

3.3节点电势法

图6所示是某电路的一部分，设a,b两点的电势分别为φa和φb，I的参考方向与Uab的方向一致，则顺着电流的流向来看，在电阻R和电源的内阻r上都存在电势降低，降低量为I(R+r)，而经过电源E1，电势降低E1；经过电源E2，电势升高E2，所以对图6所示的电路，有

φa-IR-Ir1-E1+E2-Ir2=φb

从而

Uab=I(R+r1+r2)+E1-E2

我们称之为一段含源电路的欧姆定律.由该定律可得

其中电源电动势的方向和参考电压方向一致时E取正号，反之则取负号；而电流与参考电压方向一致时I取正号，反之则取负号.

图6

如图7所示，设c点接地，选取4个独立变量φm,φn,φf和φp，则

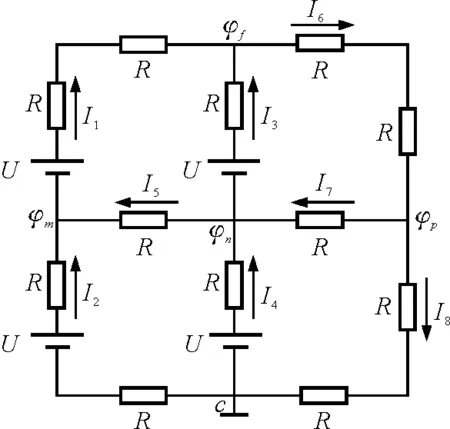
图7

因图7中有5个节点m,n,p,f,c，故可列4个独立的电流方程，分别对m,n,p和f应用基尔霍夫第一定律，有

将电流的表达式依次代入上述方程组，有

代入数据，联立求解，可得

φm=φn=φp=0.15 Vφf=0.3 V

重新代回电流的表达式，可得

I1=I2=0.025 AI3=I4=0.05 A

点评:节点电势法实际上是借助于一段含源电路的欧姆定律，以节点电势作为未知量分析电路的一种方法.适用于支路数较多，而节点数较少的电路中，同样可使方程的个数减少.解决问题的关键是选取哪些节点电势为未知量.本题中有5个节点，如令其中一个接地，则独立变量变为4个，且不影响电路中各支路电流的大小.节点电势法在解决只有两个节点的电路时显得尤为简便.

3.4对称分析法

仔细观察图3中的电路，我们会发现该电路的上下两部分是完全一样的，即电路关于中间两个电阻对称，可知I1=I2，I3=I4，I6=I8，从而中间两个电阻上的电流I5和I7必为零，故我们对图3可做以下两种等效处理：

第一，从电流为零的角度来看，可将中间两个电阻等效断开，电路如图8所示.

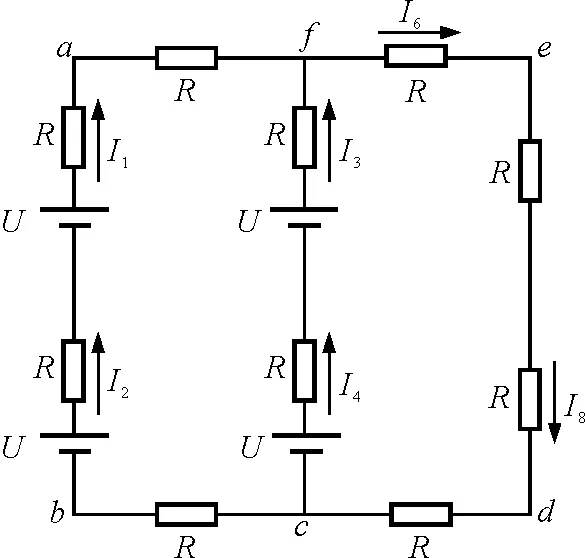
图8

第二，因两个电阻的电流为零，则每个电阻上的电压也为零，电阻两端为等电势点，故也可将中间两个电阻等效为短路.

两种等效方法对于I1,I2,I3,I4,I6,I8而言没有影响.

图8可进一步简化为图9所示的电路.

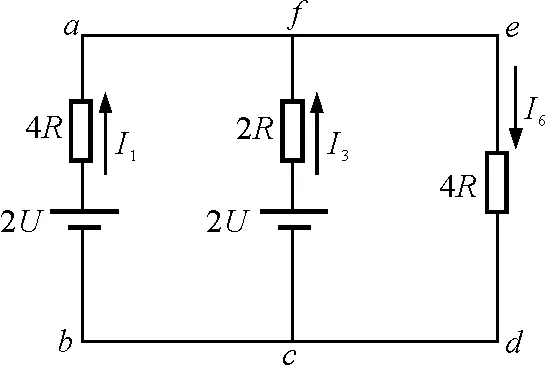
图9

对于图9，我们除了可以用上面提到的支路电流法、网孔电流法和节点电势法轻松求解之外，还可以利用以下3种方法.

方法1：叠加定理

叠加定理是线性电路的一种重要方法，其内容是：由线性电阻和多个电源组成的线性电路中，任何一个支路中的电流(或电压)等于各个电源单独作用时，在此支路中所产生的电流(或电压)的代数和.

图10

分别作出图9中的两个电源单独作用时的电路图，如图10(a)和(b)所示.图10(a)中

图10(b)中

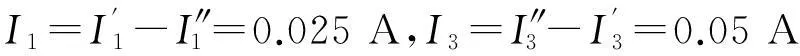
点评:叠加定理采用的是先分后合的思想，只对线性电路成立，对非线性电路则不适用，如电路中存在二极管、三极管等非线性元件.此外，该定理只能用来进行电流、电压的叠加，而不能进行功率的叠加，这是因为功率与电流、电压为二次方关系，即

P=I2R=(I′+I″)2R≠I′2R+I″2R

同时在除去电源时应注意保留其内阻.

方法2：戴维南定理

戴维南定理也叫等效电压源定理，即对外电路来说，一个含源二端线性网络可以用一个电压源来代替，该电压源的电动势E0等于二端网络的开路电压，其内阻R0等于含源二端网络内所有电源电动势为零，仅保留其内阻时，网络两端的等效电阻(即输入电阻).

根据戴维南定理可以对一个含源二端网络进行简化，简化的关键在于正确求出含源二端网络的开路电压和等效电阻.

下面用戴维南定理求图9中的电流I1.

移开图9左边的待求支路，如图11(a)所示，该二端网络的开路电压

即等效电源的电动势为

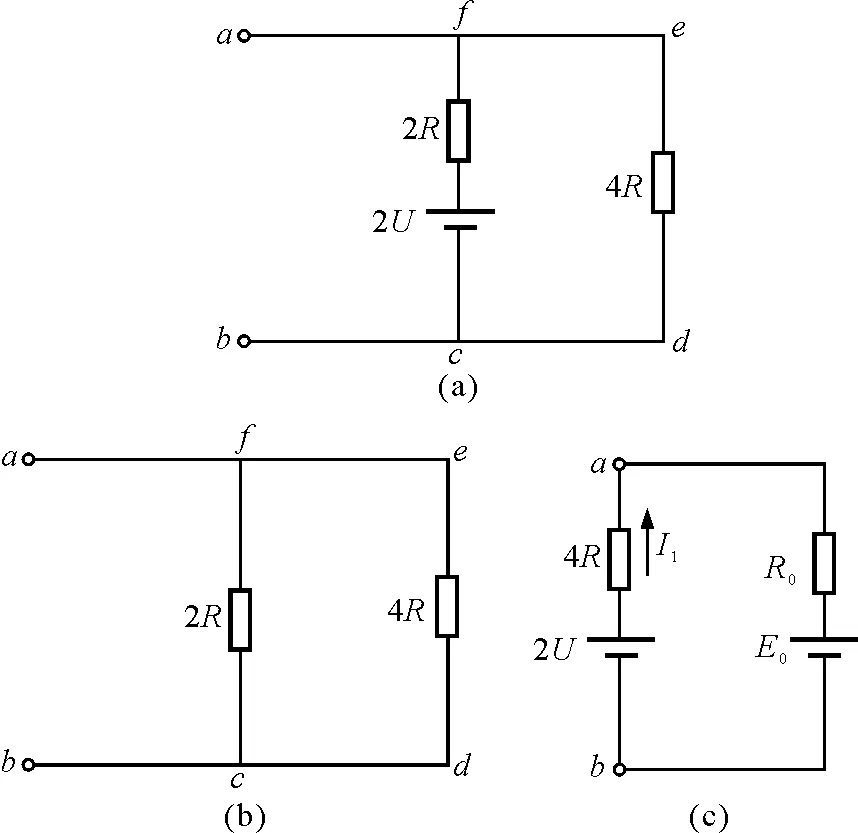
图11

再求二端网络的输入电阻Rab，这时将电源电动势除去，如图11(b)所示，则

画出ab端对应的等效电压源，并将待求支路接入，如图11(c)所示，可求得

I3的求解过程同上，但是我们在求出I1后，不一定非要再用一次戴维南定理求I3，也可以在图9中用求得的I1结合基尔霍夫两个定律计算出I3的大小.

点评:在实际问题中，遇到一个复杂直流电路，如果并不需要把所有的支路电流都求出来，在这种情况下，用基尔霍夫定律来计算就很复杂，而应用戴维南定理就比较方便.

戴维南定理的两个关键步骤：求开路电压Uab和等效电阻Rab.在计算开路电压Uab时，必须注意代替含源二端网络的等效电压源E0的极性应与开路电压Uab保持一致，如果求得的Uab是负值，则电动势E0的极性应与图11(c)中的极性相反；求等效电阻Rab时，必须将网络内的各个电源除去，仅保留电源内阻.

戴维南定理只适用于二端网络以及二端网络内部为线性电路的情形，如果二端网络内有非线性元件(如二极管、三极管等)，或者所求部分为三端网络(如三相负载)，则不适用，但如果所求支路中含有非线性元件，戴维南定理同样适用.

在高中物理电学部分，戴维南定理也常被我们用来作为电路分析的一种有效方法，如求解负载的最大功率问题、测定电源的电动势和内阻中的实验误差分析等.

方法3：Y-△变换

如图12(a)和(b)所示是一个Y形电阻网络和一个△形电阻网络，当这两个电阻网络分别接到同一个电路中时，如能保持这个电路中其余各部分的电流和电压不变，则这两个电阻网络对于这个电路是等效的.

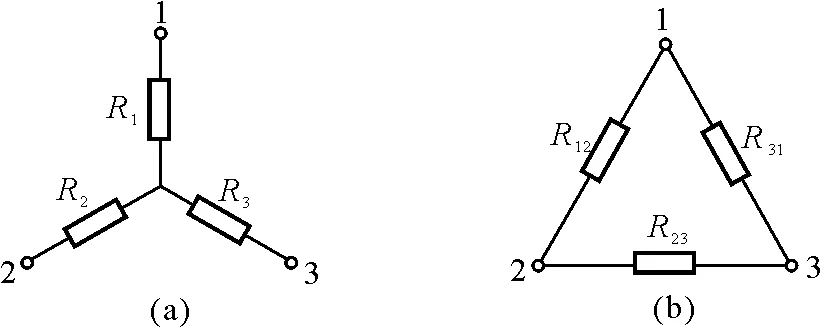
图12

Y形电路等效变换成△形电路的条件为(证明过程略)

△形电路等效变换成Y形电路的条件为

观察图9中的3个电阻4R,2R,4R，可以发现它们是Y接法，将其下端分别标上数字“1”、“2”、“3”，如图13(a)所示.用Y-△等效变换法将此Y形接法变换成△形接法，如图13(b)所示，对应的△形接法中等效电阻为R12=8R,R13=16R,R23=8R.

由图13(b)可知，电阻R12上电压为零，故电流也为零，可将R12等效为断开，且对I1和I3无影响，则

图13

点评:Y-△电路的等效变换属于节点电路的等效，在应用中，除了正确使用电阻变换公式计算各电阻值外，还必须正确连接各对应节点.

Y-△变换所说的等效是对外部电路等效，对内部不成立.如本题中的这种变换对于外电路，即图13(a)中虚线所圈外面的两个电源和一根导线而言是等效的，不会改变I1,I3和I6的大小，而对虚线所圈内部的3个电阻来讲是不等效的.

(收稿日期：2015-10-23)