计算机能耗理论下限推导的教学探讨——针对新概念物理教程·热学

汪中明　王笑君

(华南师范大学物理与电信工程学院　广东 广州　510006)



计算机能耗理论下限推导的教学探讨
——针对新概念物理教程·热学

汪中明王笑君

(华南师范大学物理与电信工程学院广东 广州510006)

摘 要：新概念物理教程热学中将玻尔兹曼熵和信息熵相比得到计算机处理信息能耗的理论下限，受限于篇幅的原因，作者讲解较为简略，给学习者对知识的理解增加了难度.本文就课本中的处理方法提出几点疑问，进一步给出计算机处理信息能耗理论下限的一般解释.在此基础上就当前一些学者认为玻尔兹曼熵与信息熵等价的观点作出辨析.

关键词：信息熵玻尔兹曼熵新概念物理能耗

新概念物理教程·热学是赵凯华先生主笔的新概念物理教程中的第二卷，与传统的物理教程相比，改革力度大，强化了熵的概念的教学，引进了量子统计的概念，还加强了热学与其他学科之间的联系，教育性、可读性都大大增加，为人称道.受限于篇幅的原因，教材作者在诸多拓展性知识点上采取了简略描述或以小字来讨论，类似作画中精彩的留白，作者对知识详略有序的处理也给教师和学生在教和学的过程中留下了更多的探讨空间.

1新概念物理教程热学中计算机处理能耗下限的推导及问题的提出

热学卷第二章7.3节“信息熵与遗传密码”一节中，在给出了信息熵的一般性介绍以后，教材作者引入了计算机处理信息能耗下限的推导：

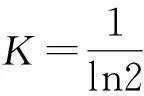
1bit= kln2 = 0.957×10-23J/K

热力学的熵增加原理告诉我们，要使计算机里的信息量存储增加1bit，它的熵减少kln2，这只能以环境的熵至少增加这么多为代价，即在温度T下处理每个bit，计算机至少消耗能量kTln2.这是能耗的理论下限.

赵先生将信息熵与玻尔兹曼熵相比，从而得到计算机处理每比特的信息至少消耗kTln2的能量看起来很是巧妙，但是，在给出信息熵与玻尔兹曼熵具体的概念界定前，我们先提出这样一些困惑：

(1)信息熵与遗传密码一节中指出，信息熵是对某种状态做出完全判断所缺的信息量.它意味着信息量的缺损，那么信息熵描述的状态和玻尔兹曼熵描述的状态是否一致，信息熵的定义域是什么？

(2)玻尔兹曼熵是从能量的角度描述一个系统微观粒子的状态，量纲为J/K，而信息熵依存于某个事件发生的概率，量纲为bit，二者的量纲截然不同，将二者对比得到计算机处理信息能耗的理论下限，其依据是什么呢？

(3)玻尔兹曼熵与信息熵之间的关系具体是怎样的，真的如许多学者提出的二者是等价的吗？

2计算机能耗理论下限的进一步解释

基于以上问题，为了得到计算机能耗理论下限的进一步解释，我们先明确信息熵与玻尔兹曼熵的概念.

2.1信息熵

1948年美国工程师和数学家克劳德·香农在《贝尔系统技术杂志》上发表论文《通信的数学理论》，奠定了信息论的基础.香农指出,“通信的基本问题是在一点精确地或近似地恢复另一点所选择的消息.”信息论中把香农指出的另一点选择的消息称为信源，恢复消息的这一端为信宿，那么对信源信息量的度量就是信息论需要解决的首要问题.

香农将信源限制为具有某一先验概率的随机过程，并借鉴了热力学中的玻尔兹曼熵概念，用信息熵来度量事件选择中含有多少“选择的可能性”，或者说用信息熵来度量选择的结果具有多大的不确定性.其表达式为

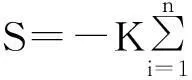
式中i表示事件有i=1,2,…,N共N种可能性，各种可能性的概率为Pi，负号表明该信息是待观测的，常数K取决于对数底a的值.

现代计算机普遍采用二进制方式存储信息，用0和1表示两种可能性，信息论定义在两种可能性中做出判断所需的信息量为1比特(bit),那么a的值为2.当信源中每一个随机事件发生的概率Pi相等时，用二进制度量信源的信息，信息熵就是

S=-KlnP

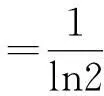
2.2玻尔兹曼熵

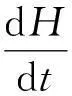
S=-klnΩ

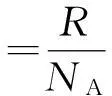
2.3对将信息熵与玻尔兹曼熵对比得出计算机能耗理论下限的进一步解释

一个孤立的系统，采用计算机二进制的算法，对系统(或者说是信源)做一次判断，由于各个微观状态之间是相互独立的，那么系统的未知状态数减少一半，通过一次判断获得信息，则此孤立系统的未知状态数减少，即信息熵减少；同样，由于判断确定了一个量子态，此孤立系统的总的量子态数降低，对应的玻尔兹曼熵在降低.而热力学熵增加原理指出，当热力学系统从一平衡态经绝热过程到达另一平衡态时，它的熵永不减少.所以，此孤立系统的热力学熵降低，必然导致其外界环境的熵增加，且系统降低的热力学熵与环境增加的热力学熵相等.我们把上述过程用公式表示出来.

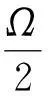
判断前孤立系统信息熵为

判断前孤立系统的玻尔兹曼熵为

S热初=klnΩ

判断后孤立系统信息熵为

判断后孤立系统的玻尔兹曼熵为

S热末=klnΩ=klnΩ-kln2

判断前、后的信息熵变

ΔS信=S信初-S信末=1bit

判断前、后的玻尔兹曼熵变

判断前、后外界环境的热力学熵变等于孤立系统的熵变

ΔS外=kln2

通过以上的表达式，我们就能很明确地看到，对一个孤立系统做一次判断，这个过程我们用两个量来描述它，一个是信息熵，一个是热力学中的玻尔兹曼熵，二者对应同一个事件状态，所以二者是一一对应的关系，即计算机做一次判断，获得1bit的信息量，系统的玻尔兹曼熵降低，导致环境的熵增加，增加了kln2.即当环境温度为300 K时，计算机处理每1bit，至少消耗约为3×10-21J的能量.

回过头看赵凯华先生推导计算机能耗理论下限的过程，其实理论上完全没有问题，只是由于为了部分语言上的精简和突出玻尔兹曼熵与信息熵的“相似性”，如“它和玻尔兹曼熵的公式极为相似”、“两者相比”，给学生阅读和教师教学操作上，带来了一定的难度，让读者不容易理解的是直接将玻尔兹曼熵与信息熵相比就在物理意义上得出计算机能耗的理论下限，这中间还差一道鸿沟没有跨越.

事实上，对于教师来说，如果换一种说法，会让理解上的难度大为降低：计算机采用二进制做一次判断，对应的信息熵就是1bit，也是在两种微观量子态中作出判断，所以量子态的数目就是2，对应的玻尔兹曼熵就是kln2，这样我们就可以说“要使计算机里的信息量存储增加1bit，它的熵减少kln2，这只能以环境的熵至少增加这么多为代价，即在温度T下处理每个bit，计算机至少消耗kTln2焦耳的能量”.所以，严格来说

1bit =kln2 = 0.957×10-23J/K

这个等式是存在问题的，因为1bit对应的是信息熵，从前面对信息熵概念的描述我们知道，信息熵本没有单位，我们只是人为地规定把从两种可能性中作出判断所需的信息量叫做1bit.而玻尔兹曼熵的单位是J/K，等式前后的量纲完全不同，用等号将二者建立等量关系显然是不合理的，合理的处理方式应该是我们在物理意义上将二者建立对应关系.

3教学上的拓展延伸——信息熵与玻尔兹曼熵关系的辨析

基于赵先生的理论建立起了连通信息论和热力学的桥梁，学生在学完这一节以后，会很自然地有一个困惑，就是信息熵与玻尔兹曼熵的关系.我们就此来对他们作一个明确的辨析，也是对前文提出的第3个问题的回答.

许多学生甚至是学者将玻尔兹曼熵与信息熵视为等价，一定程度上因为二者都是建立在概率的基础上.对于玻尔兹曼熵，如前文对玻尔兹曼熵的介绍，lnΩ= -H，它的值涉及到所研究系统微观状态的数目，微观量子态的数目越多，其对应的宏观状态出现的概率就越大.对于信息熵来说，信宿要对信源作出完全判断所缺的信息量，当信源中包含的事件可能性越多，需要作出判断的次数也就越多，信息熵也就越大.所以，本质上看，二者都是从概率的角度出发，熵的大小由概率决定，但能否因此说二者是等价的呢，显然是还远远不够的，我们不能就此而忽略玻尔兹曼熵与信息熵之间存在的巨大差异.

玻尔兹曼熵中的Ω是微观粒子状态的数目，它以系统中每一个微观粒子的状态为统计单元；而在信息论中，信息是通过认识主体的感受而体现出来的，信息熵中每一个元事件的确定则要受制于信源传递了什么样的信息.比如掷两颗骰子，当信源传递的是两颗骰子正面朝上的点数之和的大小时，那么“两颗骰子正面点数之和”为从2到12这几个特定的数之一，这个状态就是一个元事件，共有11种状态，当信源传递的是两颗骰子点数的奇偶性时，那么“同奇、同偶、奇偶”就是对应的3种元事件.所以，信息熵从信息缺损的角度来描述一个事件，显然这是受制于主观能动性的，一千个读者就有一千个哈姆雷特，对同一个事件，不同的人所需要的信息是不一样的，信息熵的大小也会有所差异，因而具有主观性.而对于物理中的一个宏观系统，其微观粒子总的状态数仅由一定体积中粒子的数目和环境的温度决定，是客观实在的.就如同普朗克在《论热力学》一书中所说， “这个定律的局限存在于受观测的自然，而不在于观测者.这个定律的演绎所要求的是人的经验是无足轻重的”.所以理论上我们可以用信息熵描述完全判断某一系统微观量子态所需要的信息量，但不能用玻尔兹曼熵去描述非微观物理意义上的概率事件.两种熵都基于概率，但实际上他们对概率的定义方式截然不同，这也必然导致二者之间存在巨大差异.

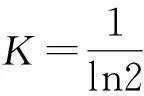
综上，我们用一副图(图1)来辨析一下信息熵与玻尔兹曼熵二者之间的关系.

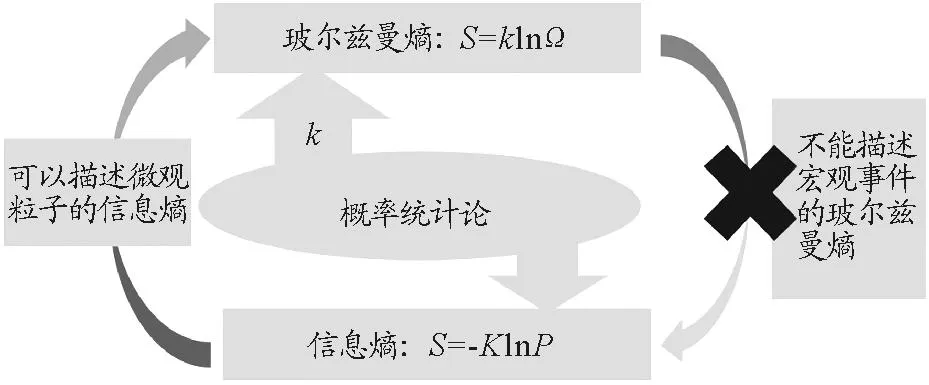
图1　玻尔兹曼熵与信息熵之间的关系

玻尔兹曼熵是在统计的角度上建立起了系统宏观状态与微观量子态的关系，从而反映出热力学第二定律中熵增加原理的本质是概率法则在起作用.信息熵中，概率法则决定了对某一事件作出判断所缺的信息量的多少.它们都是从概率统计的角度出发的，在一定程度上可以建立起联系，二者的表达式十分相似，但实则两个熵中概率的描述范围受限于各自的条件，不同的比例系数也决定了二者向两个完全不同的学科方向发展.所以玻尔兹曼熵与信息熵是完全不等价的.

4教学中的总结与反思

信息熵与遗传密码一节是以小字展出的，在教学中的地位并不重要，但我们不能忽视熵在物理学中发挥的越来越基本、越来越重要的角色，从物理学走向化学、生命科学等学科中，熵的重要性也越来越突出.教师在教学中首先自己要明确信息熵与玻尔兹曼熵的关系，然后用更加简单的方法讲清楚将玻尔兹曼熵与信息熵对比从而得出计算机能耗理论下限的过程,以加深学生对熵概念的认知，提高他们的学习兴趣，同时还能够为后续热力学统计物理的学习打下基础.

参 考 文 献

1赵凯华，罗蔚茵. 新概念物理教程·热学.北京：高等教育出版社，2005

2田宝玉，等. 信息论基础.北京：人民邮电出版社，2008

3李鹤龄. 信息熵、玻尔兹曼熵以及克劳修斯熵之间的关系——兼论玻尔兹曼熵和克劳修斯熵是否等价. 大学物理,2004(12):37～40

Discussion on Teaching of Deriving Theoretical Lower Limit of Computer Energy Consumption

Wang ZhongmingWang Xiaojun

(School of Physics and Telecommunication Engineering, South China Normal University, Guangzhou, Guangdong510006)

Abstract：There is a method compare Boltzmann entropy with Information entropy for getting the lowest energy consumption of computer in Heat of new concept physics. Limitation of space forbids full treatment of the subject which bring the difficulty to readers in understand. The article put forward some questions on how to get lowest energy consumption then give explain further for understand easily, and we also discussed the relation between Boltzmann entropy and Information entropy at last.

Key words:information entropy; boltzmann entropy; new concept physics; energy consumption

(收稿日期：2015-11-10)