多源异构超紧组合非线性信息互耦合方法及特征分析

谢 非，赵 静，钱伟行，康国华

（1. 南京师范大学 电气工程与自动化学院，南京 210042；2. 南京邮电大学 自动化学院，南京 210023；3. 江苏省三维打印装备与制造重点实验室，南京210042；4. 南京航空航天大学 微小卫星研究中心，南京 210016）

多源异构超紧组合非线性信息互耦合方法及特征分析

谢 非1,3，赵 静2,3，钱伟行1，康国华4

（1. 南京师范大学 电气工程与自动化学院，南京 210042；2. 南京邮电大学 自动化学院，南京 210023；3. 江苏省三维打印装备与制造重点实验室，南京210042；4. 南京航空航天大学 微小卫星研究中心，南京 210016）

惯性/卫星超紧组合技术核心将卫星导航接收机基带信号处理过程中的环路非线性信息与惯性导航信息进行深层次互耦合。在研究超紧组合多信息源异型耦合架构特征及互耦合机理的基础上，对比分析了超紧组合非相干及相干互耦合方法，总结了不同超紧组合观测矢量提取方法及环路模型，然后设计了超紧组合互耦合信息处理流程及信号NCO（数控振荡器）控制方法。最后，利用仿真平台对非相干及相干方式进行了卫星信号受干扰及载体动态变化环境下的试验对比分析，结果表明超紧组合相干方法相较于非相干方式具有更优的观测矢量提取性能及抗干扰性能。

超紧组合；组合导航；卫星接收机；抗干扰

近年来，在卫星导航抗干扰及高动态适应性能需求牵引下，惯性/卫星超紧组合（Ultra-tightly INS/GNSS coupled）技术逐渐被提出并引起关注[1]，为改善卫星导航脆弱性提供了新的技术途径。我国北斗卫星导航系统的自主建设也为超紧组合技术发展提出迫切需求。

惯性/卫星超紧组合技术核心将卫星导航接收机基带信号处理过程中的环路非线性信息与惯性导航信息进行深层次互耦合，并最终实现惯性系统和卫星接收机性能的相互辅助与提高。美国Draper实验室通过研究非线性超紧组合算法，从而将GPS接收机环路相关器的非线性信息与微惯性系统解算的位置、速度、姿态及传感器误差等状态进行耦合[2]；加拿大Calgary大学的Lachapelle教授团队针对超紧组合架构模型、观测量提取方式、耦合滤波器设计及样机开发等方面开展了深入研究[3-5]。此外，美国的IGS LLC（Honeywell与Rockwell Collins合资）公司、CRS公司、Auburn大学及澳大利亚的UNSW大学[6-10]等均针对超紧组合环路非线性信息处理与融合等方面开展了相关研究。

本文针对惯性/卫星超紧组合的架构特征及非线性信息互耦合机理进行分析，在此基础上讨论了超紧组合非相干及相干互耦合方法特点及观测矢量提取模型，最后对信号干扰及动态变化环境下的不同超紧组合耦合方法进行了实验对比与分析。

1 惯性/卫星超紧组合架构及互耦合机理分析

1.1 惯性/卫星超紧组合多源异型耦合架构分析

传统的惯性/卫星组合导航系统以松、紧组合两种模式为主[11-12]，此时，卫星接收机采用传统标量跟踪结构进行信号的锁定与解调，并且多个跟踪通道之间无任何信息交互，也无法借助其他外部信息（如惯性信息）对环路信号跟踪进行控制。因此，一旦接收机受到信号干扰或载体较高动态影响，容易出现环路信号失锁乃至导航定位失效问题[13]。

针对这一问题，从惯性导航系统与卫星导航内部的信号处理架构层面考虑改变组合体制与耦合方式，通过将惯性信息与卫星接收机基带信号跟踪处理进行深层次融合，形成了惯性/卫星超紧组合导航架构[14]。与松、紧、惯性辅助三种组合模式相比，超紧组合架构的最大特点在于其信息耦合的来源更为丰富且组合的层次也更为深入，同时，惯性导航系统和卫星接收机均不再保持各自独立的工作状态，而是采用接收机环路内部非线性相关结果中隐含的相位、频率参量作为观测量，通过建立组合滤波器耦合模型进行惯性与接收机矢量环路信号的信息融合，同时利用惯性导航结果直接控制环路架构中本地伪码及载波信号生成，以完全断开接收机中传统标量环路的反馈控制，实现惯性和接收机的深度互耦合。

1.2 惯性/卫星超紧组合信息互耦合机理及模型分析

由于载体与卫星间相对运动因素的影响，使得卫星导航接收机接收到的卫星信号伪码相位及载波频率处于不断的变化之中，而超紧组合导航技术则是利用了信号参量变化与载体及卫星相对运动之间内在关系，实现了矢量环路信号及惯性导航信息间的深度耦合作用，这也正是惯性/卫星超紧组合中信息融合的内在机理。

本文通过卫星接收机矢量环路信号模型的建立及相关结果与载体运动状态关联进行超紧组合信息融合机理分析。为了说明卫星接收机环路内部相关积分结果及码相位偏差及载波频率偏差间的内在关联，环路即时相关积分值可由以下数学模型表示：

式中：iP、qP为I、Q两个支路的即时相关结果；Tc为相关积分时间长度；A为相关积分幅值；D(·)为导航电文数据比特电平值；R(·)代表伪码自相关函数；δτ为本地复制码与接收码的相位差异；ωe、fe、θe、φe分别代表复制载波与接收载波之间的角频率差、频率差、初相差及相位差。

卫星导航接收机在载波解调及伪码解扩过程中一方面根据自相关主峰位置获得伪码信号的相位并将其转化为伪距测量值，用于位置解算，另一方面获得多普勒频移并将其转化为伪距率测量值，用于速度解算。因此，相位及频率的变化分别映射了伪距及伪距率的变化，而伪距及伪距率的变化则同接收机与卫星运动视线方向上的几何关系密切关联，伪码相位偏差与位置误差关联示意图如图1所示。

图1 相位误差与接收机位置误差关联示意图Fig.1 Schematic of correlation between phase bias and receiver position bias

如果利用惯性系统提供的实时载体状态对本地复制伪码相位及载波频率进行估计，则可进一步获得超紧组合环路中伪码相位偏差（已转换为距离值，单位m）及载波频率偏差（单位Hz）与惯性导航状态误差之间的关联模型如下：

1）伪码相位偏差关联模型：

2）载波频率偏差关联模型：

因此，从式(1)～(4)的模型中可以看出，超紧组合利用接收机环路内部非线性相关信息中所蕴含的码相位偏差及载波频率偏差作为观测量，以对惯性导航状态（位置、速度）误差进行估计，从而完成惯性与接收机环路信息的深度融合。因此，选择合适的非线性信息估计方法，对超紧组合系统中观测信息的提取质量有着重要作用。

2 惯性/卫星超紧组合非线性互耦合方法分析

2.1 惯性/卫星超紧组合互耦合方法分析

超紧组合的典型特点在于其采用了环路非线性相关积分结果（I、Q）中隐含的相位及频率信息与惯性导航信息进行耦合，为了获得较为精确的相位及频率参量，需从相关积分结果中提取有效的观测矢量信息。

目前，针对超紧组合的观测信息提取主要包括了两种方式：一种是以环路鉴相器输出作为导航滤波器观测量的非相干方式（Non-Coherent）；另一种为利用环路子滤波器提取导航滤波器观测量，并将相关积分结果作为子滤波器观测量的相干方式（Conherent）[15]。1）超紧组合非相干互耦合方式

非相干方式利用通道跟踪卫星到接收机位置视线方向上的状态（位置、速度）误差与码相位及载波频率之间的内在关系，将相关积分结果I、Q通过鉴相/鉴频器输出得到的接收信号和本地信号的相位和频率偏差转换为伪距偏差和伪距率偏差，然后作为组合滤波器的观测量，实现对惯性导航系统状态分量的估计及校正。对于现实中的卫星接收机来讲，由于接收信号的相位及频率时常包含着短暂的、小幅度的随时间变化的高阶激励成分，因此，在非相干方式的应用过程中，经常采用观测预处理滤波器的设计来进一步消减低阶滤波器产生恒定相位及频率跟踪误差。超紧组合非相干耦合方法结构框图如图2所示。

图2 超紧组合非相干耦合方法结构框图Fig.2 Block diagram of non-coherent ultra-tight integration

对于卫星载波跟踪环路，最终目的是产生本地信号，令本地信号和输入信号的相位差为 0。通过环路状态估计可以得到当前时刻（k时刻）的码相位差δkτ、载波相位差Δkθ、信号载波频率差Δkω以及信号载波频率差的变化率之间的相互关系。按此状态外推k+1时刻的码相位差及载波相位差分别为：

码环和载波环中的鉴相器分别估计了本地信号和输入信号的码相位差以及载波相位差。由于鉴相器的输出一般是线性的（或者近似线性），为了更好地利用鉴相器特性及进一步降低预处理滤波器设计复杂性，在非相干超紧组合观测预处理滤波器中采用码及载波鉴相器输出结果作为观测量，而状态方程为：

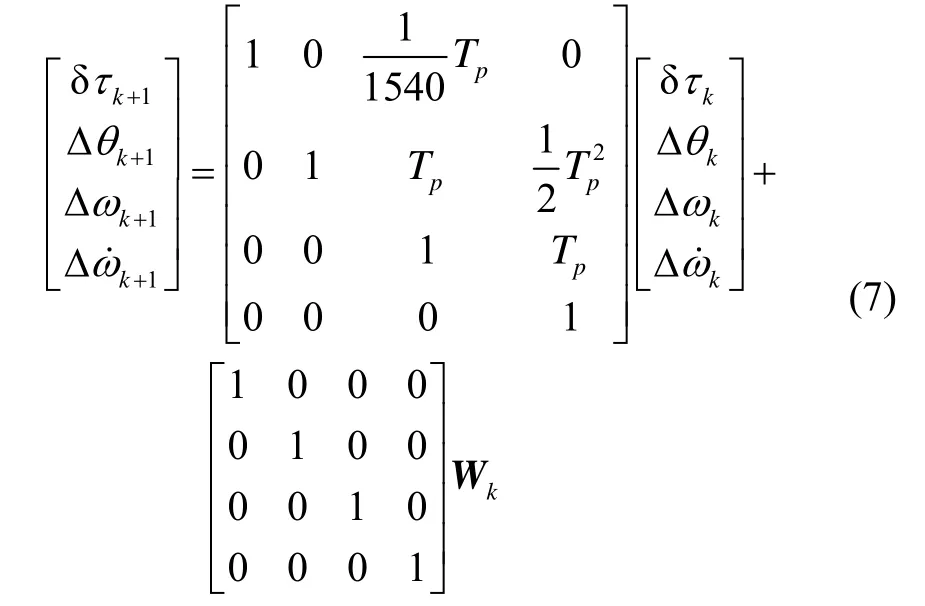
此外，接收机环路相关器输出频率可通过相干积分时间或非相干积分时间进行调整，而观测预处理滤波器的引入也可将组合导航滤波器的更新率减小到10～100 Hz，从而降低了高阶组合滤波器的运算负担。2）超紧组合相干互耦合方式

而在相干方式中，卫星接收机直接将跟踪环路各通道相关积分输出值I和Q送至子滤波器或组合导航滤波器作为观测量，对本地伪码及载波信号的相位、频率参量及惯性系统输出状态分量进行估计。其优点是不采用环路鉴相/鉴频器，避免了鉴相/鉴频器引入的无法建模的高阶非线性因素，降低观测矢量中的跟踪误差及噪声分量。但是，由于卫星接收机基带信号处理通道相关输出中均含有同相与正交的6路相关积分结果，因此，对N通道的接收机系统来说，即有N×6组观测矢量送入组合导航滤波器中，会引起系统观测阶数较高以致组合导航滤波器的计算负荷较大问题。在实际处理过程中，相干耦合方式通常利用环路子滤波器构建来减小环路高阶相关观测信息处理运算量。超紧组合相干耦合方法结构框图如图3所示。

图3 超紧组合相干耦合方法结构框图Fig.3 Block diagram of coherent ultra-tight integration

相干耦合架构中，由于子滤波器的目标同为提取接收信号与本地信号之间的相位偏差δτk及频率偏差Δωk，因此其状态矢量选择及状态方程设计同非相干方式。而观测方程模型如下：

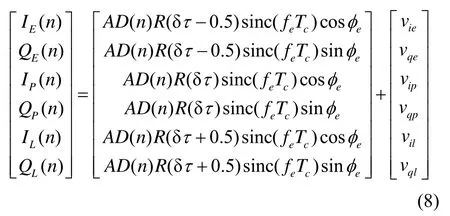
此外，由式(8)可以看出，环路相关积分结果与状态分量相位偏差δτk及频率偏差Δωk=2πfe之间存在着较强的非线性耦合关系，因此，相干耦合超紧组合的子滤波器一般选取适用于I/Q参量非线性特征的状态估计器（Unscented Kalman Filter，UKF或Extended Kalman Filter，EKF等）[16]来提高系统的观测范围及观测矢量的状态估计精度。其中，UKF方法是在卡尔曼滤波框架基础上，通过UT（Unscented Transform）变换方式，用一定数量采样点对非线性密度函数进行逼近。同EKF方法相比，UKF方法计算量与EKF同阶次，但却避免了实际应用中较难获得非线性函数雅克比矩阵的问题。事实上，相干耦合方式中的子滤波器往往也是对环路信号参量进行估计，因而与非相干耦合方式本质上是相同的。

2.2 惯性/卫星超紧组合信息互耦合流程分析

超紧组合系统核心是将卫星导航接收机中基带信号解调处理和惯性导航信息进行深层次互耦合，除了建立导航滤波器互耦合模型及采用相关器输出参量作为其观测量之外，还需断开卫星接收机传统标量跟踪环路中本地信号的反馈控制通道，利用修正后的惯性导航结果直接控制矢量环路中本地伪码及载波信号生成，如图3所示，完成对惯性导航状态和接收机环路信号参量的估计，实现惯性和卫星接收机环路信息的深度耦合及双向辅助。惯性/卫星超紧组合互耦合方法信息处理流程为：

1）对惯性传感器组件测量信息进行采集处理，并基于惯性导航解算原理完成本周期惯性导航位置、速度、姿态等状态的解算；

2）卫星接收机对下变频后的中频信号进行基带多通道信号相关及解调处理，环路信号经伪码解扩及载波解调后输出六路相关积分结果；

3）判断环路信号周期，提取预处理滤波器或子滤波器的观测量，并按设定周期将观测量送入导航滤波器中进行信息耦合；

4）利用导航滤波器输出结果校正惯性导航状态并输出，同时利用校正状态实现对环路伪码及载波NCO控制和本地信号相位及频率的调整，进行下一周期环路信号的相关处理及导航信息的耦合解算。

最后，为了实现接收机跟踪环路本地信号的矢量控制，需利用外部惯性信息估计码环NCO及载波环NCO控制量。本地码NCO控制调整量的计算方法如下：

式(9)中包括了两种控制分量计算：第一为接收机和第i个通道跟踪卫星之间相对位移变化产生的伪码相位变化（即为码频率偏移量），其计算方法如式(10)所示；第二部分为接收机和卫星间的相对运动产生的多普勒频移变化导致的码频率偏移，见式(11)。

在对卫星接收机跟踪环路本地信号进行控制的过程中，式(9)及(11)计算的频率调整量为下一周期相对上一周期的NCO控制频率变化量，该控制量的输入对原有跟踪环路的冲击非常微弱，因此对保持环路的跟踪稳定性具有良好的支撑作用。

3 实验与分析

为了对比分析不同耦合架构超紧组合观测性能，利用搭建的惯性/卫星超紧组合仿真实验平台分别对非相干及相干互耦合方式进行测试，实验模拟了信号受噪声干扰环境下能量衰减及载体动态变化两种场景，其中动态变化过程包括滑跑、爬升、平飞、持续10 s的50 g高过载及持续20 s的恒定加加速度0.5 g/s，整个过程的三维动态轨迹如图4所示：初始阶段信号载噪比为45 dB-Hz，在平飞阶段引入噪声干扰，信号载噪比衰减至20 dB-Hz，然后再撤消干扰逐渐恢复。

图4 实验测试所用载体三维动态轨迹图Fig.4 Mimic three-dimensional dynamic trajectory designed for simulation experiments

由于非相干及相干互耦合架构的显著区别在于其对环路信号观测量的提取方式不同，因此，针对同一场景下两种架构的观测量提取结果如图5所示。超紧组合的主要目标在于利用惯性信息的耦合降低接收机环路的等效带宽及消除动态应力，并维持环路信号的跟踪状态，而环路信号的测量误差则由多源噪声引起的相位抖动噪声及动态应力抖动噪声两部分决定。此实验中多源噪声引入的总相位抖动均方差为

式中：σt,PLL为宽带热噪声引起的相位抖动，σv为用户运动及接收机装置的机械颤动引起的基准振荡频率抖动对应的相位抖动，σA为接收机晶体振荡器的艾兰型相位抖动，后两者一般相对较小，此处的环路带宽设置为BL=25 Hz，环路相关积分时间设为Tc=0.001 s。此外，接收机二阶环路在加速度为50 g动态应力作用下产生的相位跟踪误差约为

对于非相干耦合方式而言，该误差已远超过鉴相器的工作容限，虽然超紧组合系统可通过惯性导航结果抵消大部分的动态应力影响，但鉴相器输出经观测预处理滤波后仍会出现一定波动。相比较而言，相干互耦合架构由于直接将跟踪环路中各通道相关积分输出值I和Q送至子滤波器，避免了受鉴相器工作范围限制而无法鉴别相位误差的问题，因此，其观测结果受高动态应力的影响较小一些。实验场景后期在匀速运动状态下引入了恒定0.5 g/s加加速度，由于动态应力大小由卫星与接收机之间的径向运动大小决定，因此，恒定0.5 g/s加加速度对观测结果的影响相对较小。

图5 非相干及相干互耦合方法提取观测量结果对比Fig.5 Performance comparison on measurements between non-coherent and coherent mutual coupling methods

综上所述，超紧组合相干方法与非相干方法相比，虽然模型设计及算法实现上较为复杂，但避免了由于鉴相器工作范围受限及鉴相器非线性特性引入的测量噪声无法建模的问题，可以更为精确地提取超紧组合环路非线性信息中的有效观测矢量，从而间接提高了超紧组合导航滤波器的估计精度及系统的导航性能。

4 总结与展望

针对惯性/卫星超紧组合架构特征及互耦合机理分析基础上，总结了超紧组合非相干及相干互耦合方法特点及观测矢量提取模型。通过接收信号受干扰及载体动态变化环境下的环路观测性能实验进一步说明了超紧组合相干耦合方法的性能优势及特点。后续关于不同耦合方法性能分析及系统设计还需持续研究。

（References）：

[1] Li K, Zhao J X, Wang X Y, et al. Federated ultra-tightly coupled GPS/INS integrated navigation system based on vector tracking for severe jamming environment[J]. IET Radar, Sonar and Navigation, 2016, 10(6): 1030-1037.

[2] Landis D, Thorvaldsen T, Fink B, et al. A deep integration estimator for urban ground navigation[C]// IEEE/ION Position, Location, and Navigation Symposium. 2006: 927-932.

[3] Sun D, Petovello M G, Cannon M E. Ultra-tight GPS/ reduced-IMU integration for land vehicle navigation[J]. IEEE Trans. Aerospace and Electronic Systems, 2013, 49(3): 1781-1791.

[4] Bhaskar S, Curran J, Lachapelle G. Effect of oscillator quality on ultra-tight GPS/INS aided carrier phase tracking[C]//Proceedings of International Technical Meeting of the Satellite Division of the Institute of Navigation (ION GNSS). 2012: 56-66.

[5] Krasovski S, Petovello M G, Lachapelle G. Ultra-tight GPS/INS receiver performance in the presence of jamming signals[C]//Proceedings of International Technical Meeting of the Satellite Division of the Institute of Navigation (ION GNSS). 2014: 1-13.

[6] Buck T M, Wilmot J, Cook M J. A high G, MEMS based, deeply integrated, INS/GPS, guidance, navigation and control flight management Unit[C]//IEEE/ION Position, Location, and Navigation Symposium. 2006: 772-794.

[7] Lashley M, Bevly D M. Performance comparison of deep integration and tight coupling[J]. Navigation, 2013, 60(3): 159-178.

[8] Salmon D C, Bevly D M. An exploration of low-cost sensor and vehicle model solutions for ground vehicle navigation[C]//IEEE/ION Position, Location, and Navigation Symposium. 2014: 462-471.

[9] Han H, Wang J, Wang J L, et al. Performance analysis on carrier phase-based tightly-coupled GPS/BDS/INS integration in GNSS degraded and denied environments[J]. Sensors, 2015, 15(4): 8685-8711.

[10] Luo Y, Babu R. Double-filter model with modified Kalman filter for baseband signal pre-processing with application to ultra-tight GPS/INS integration[J]. GPS Solutions, 2012, 16(4): 463-476.

[11] Jamal S Z. Tightly coupled GPS/INS airborne navigation system[J]. IEEE Aerospace and Electronic Systems Magazine, 2012, 27(4): 39-42.

[12] Guo Yao, Wu Wenqi, Tang Kang-hua. A new inertial aid method for high dynamic compass signal tracking based on a nonlinear tracking differentiator[J]. Sensors, 2012, 12(1): 7634-7647.

[13] Qin F, Zhan X Q, Zhan L. Performance assessment of a low-cost inertial measurement unit based ultra-tight GPS/INS integration for high dynamic applications[J]. IET Radar, Sonar and Navigation, 2014, 8(7): 828-836.

[14] 高帅和, 赵琳. 不同GPS/SINS超紧组合框架的分析与等价性推导[J]. 中国惯性技术学报, 2011, 19(5): 571-574. Gao Shuai-he, Zhao Lin. Analysis and equivalence derivation of different ultra-tight coupled navigation structures[J]. Journal of Chinese Inertial Technology, 2011, 19(5): 571-574.

[15] Luo Y, Wu W Q, Babu R, et al. A double-filterstructure based COMPASS/INS deep integrated navigation system implementation and tracking performance evaluation[J]. Science China Information Sciences, 2012, 57(1): 1-14.

[16] Liu G, Guo M F, Zhang R, et al. Hardware-implementable vector tracking loop for GNSS/INS deep integration[J]. Journal of Chinese Inertial Technology, 2015, 23(2): 189-195.

Analysis on mutual coupling method and feature of nonlinear information in multi-source ultra-tight integration with different structures

XIE Fei1, ZHAO Jing2, QIAN Wei-xing1, KANG Guo-hua
(1. School of Electrical and Automation Engineering, Nanjing Normal University, Nanjing 210042, China; 2. School of Automation, Nanjing University of Posts and Telecommunications, Nanjing 210023, China; 3. Jiangsu Key Laboratory of 3D Printing Equipment and Manufacturing, Nanjing 210042, China; 4. Microsatellite research center, Nanjing University. of Aeronautics & Astronautics, Nanjing 210016, China)

The core technique in ultra-tightly coupled INS/GNSS is mutual coupling in deep level for INS navigation solution and nonlinear loop measurements in GNSS receiver baseband signal processing. This paper analyzes the non-coherent and coherent ultra-tight integration algorithms based on studying the feature of multi-source ultra-tight integration with different structures and mutual coupling mechanism. The estimation methods of observation vector and loop models are summarized. The information processing procedure and NCO (Numerical control oscillator) controlled methods in ultra-tight integration are designed. Simulation tests are carried out to compare the performances of non-coherent and coherent ultra-tight integration algorithms under signal interference and dynamic variation environments. Test results indicate that the coherent method can provide better performances in observation-vector-extraction and anti-jamming than the non-coherent method.

ultra-tight integration; integrated navigation; GNSS receiver; anti-jamming

U666.1

：A

2016-09-05；

：2016-11-29

国家自然科学基金（61601228，61403210）；江苏省自然科学基金（BK20161021，BK20141453，SBK201343261）；江苏省三维打印装备与制造重点实验室项目（BM2013006）资助开放课题（3DL201607）；江苏省高校自然科学基金（15KJB510016）

谢非（1983—），男，博士，讲师，从事卫星导航与组合导航技术的研究。E-mail: xiefei@njnu.edu.cn

1005-6734(2016)04-0517-07

10.13695/j.cnki.12-1222/o3.2016.04.017