EVANS FUNCTIONS AND INSTABILITY OF A STANDING PULSE SOLUTION OF A NONLINEAR SYSTEM OF REACTION DIFFUSION EQUATIONS∗†

Linghai Zhang

(Dept.of Math.,Lehigh University,14 East Packer Avenue, Bethlehem,Pennsylvania 18015 USA)

EVANS FUNCTIONS AND INSTABILITY OF A STANDING PULSE SOLUTION OF A NONLINEAR SYSTEM OF REACTION DIFFUSION EQUATIONS∗†

Linghai Zhang‡

(Dept.of Math.,Lehigh University,14 East Packer Avenue, Bethlehem,Pennsylvania 18015 USA)

In this paper,we consider a nonlinear system of reaction dif f usion equations arising from mathematical neuroscience and a system of nonlinear scalar reaction dif f usion equations under some assumptions on their coefficients.

nonlinear system of reaction dif f usion equations;standing pulse solutions;existence;instability;linearized stability criterion;Evans functions

2000 Mathematics Subject Classification 35Q20

1 Introduction

1.1 Mathematical Model Equations

Consider the following nonlinear system of reaction dif f usion equations arising from mathematical neuroscience

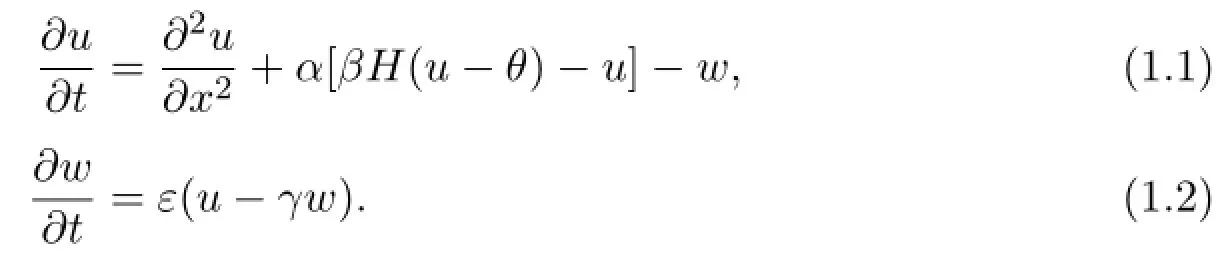
Also consider the following nonlinear scalar reaction dif f usion equations

and

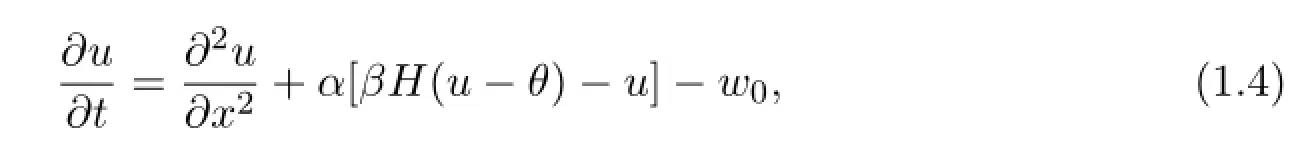
wherew0=α(β-2θ)＞0 is a positive constant.In these model equations,u=u(x,t)represents the membrane potential of a neuron at positionxand timet,w=w(x,t)represents the leaking current,a slow process that controls the excitation of neuron membrane.The positive constantsα＞0,β＞0,γ＞0,ε＞0 andθ＞0 represent neurobiological mechanisms.The positive constantθ＞0 represents the threshold for excitation.The functionH=H(u-θ)represents the Heaviside step function,which is def i ned byH(u-θ)=0 for allu＜θ,H(0)=1/2 andH(u-θ)=1 for allu＞θ.When an action potential is generated across a neuron membrane,Na+ion activation is considerably faster than K+ion activation.The positive constantεrepresents the ratio of the activation of Na+ion channels over the activation of K+ion channels.The two nonlinear scalar reaction dif f usion equations may be obtained by settingε=0,w=0 andε=0,w=w0,respectively,in system(1.1)-(1.2).See Feroe[5-7],McKean[8-10],McKean and Moll[11],Rinzel and Keller[12],Rinzel and Terman[13],Terman[14],Wang[15]and[16]for more neurobiological backgrounds of the model system.

1.2 Main Difficulty,Main Purposes and Main Strategy

Note that there exists neither maximum principle nor conservation laws to the nonlinear system of reaction dif f usion equations.The existence and instability of standing pulse solutions of the system are very important and interesting topics in applied mathematics,but they have been open for a long time,except for some numerical simulations and some claimed results without rigorous mathematical analysis.The strategy to overcome the main difficulty:coupling together linearized stability criterion and Evans functions seem to be the best way to approach the instability of the standing pulse solutions.

The main purpose of this paper is to accomplish the existence and instability of standing pulse solutions of the nonlinear system of reaction dif f usion equations(1.1)-(1.2)and the nonlinear scalar reaction dif f usion equation(1.3).The existence of the standing pulse solutions of both(1.1)-(1.2)and(1.3)follows from standard ideas, methods and techniques in dynamical systems.The instability of the standing pulse solutions will be accomplished by coupling together linearized stability criterion and Evans functions.The interesting and difficult points are that the eigenvalueproblems obtained by using linearization technique and the method of separation of variables involve the Dirac delta impulse functions.This makes it very difficult to establish the equivalence of the nonlinear stability,the linear stability and the spectral stability of the standing pulse solutions.Another very interesting point is that the parameterεplays no role in the existence of the standing pulse solutions, but it plays a very important role in the instability of the standing pulse solutions.

The construction and application of Evans functions to stability analysis of standing pulse solutions of the nonlinear system of reaction dif f usion equations(1.1)-(1.2)have been open for a long time.This paper aims to provide positive solutions to the open problems.The introduction of the Evans function and the study of the instability of the standing pulse solutions have strong impacts on stability of fast multiple traveling pulse solutions.Mathematically and biologically,these are very important/interesting problems.We believe that the same ideas also work for the existence and stability of fast multiple traveling pulse solutions and the existence and instability of slow multiple traveling pulse solutions of system(1.1)-(1.2).

1.3 Main Results

Theorem 1 (I)Suppose that the positive constants α＞0,β＞0,γ＞0, ε＞0and θ＞0satisfy the conditions0＜2(1+αγ)θ＜αβγ.Then there exists a unique standing pulse solution(U,W)∈C1(R)∩C2(R-{0})to the nonlinear system of reaction dif f usion equations(1.1)-(1.2).The standing pulse solution is given explicitly by

(II)The standing pulse solution is unstable.

(III)Suppose that the positive constants α＞0,β＞0and θ＞0satisfy the conditions0＜2θ＜β.Then there exists a unique unstable standing pulse solution U∈C1(R)∩C2(R-{0})to the nonlinear scalar reaction dif f usion equation(1.3). The standing pulse solution is given explicitly by

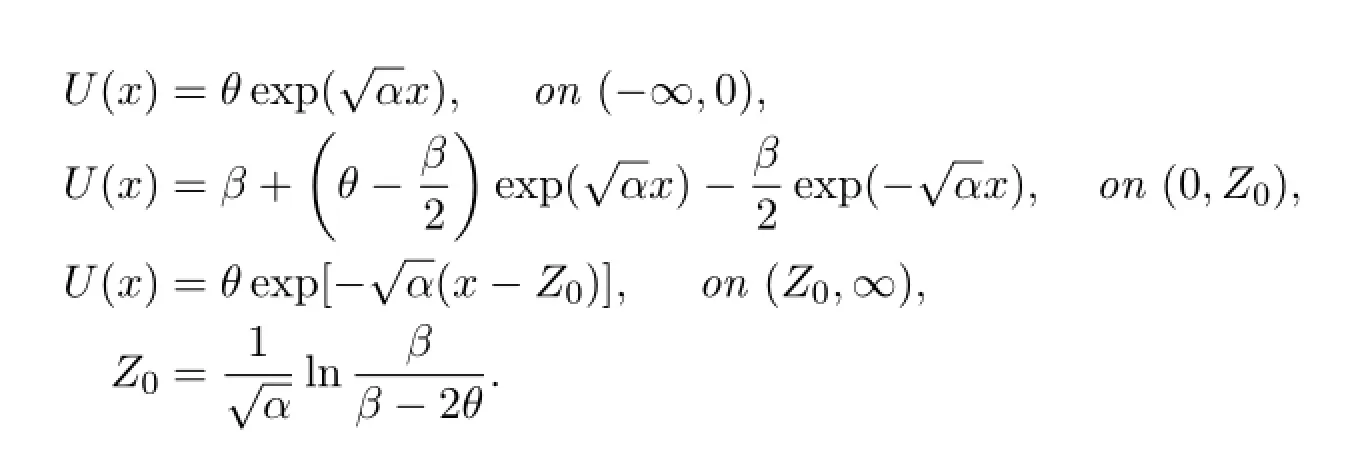
1.4 Previous Related Results

In early papers,the existence and instability of the standing pulse solutions had been announced to be true.For the existence and instability of the standing pulse solutions,the previous analysis missed a few key points.One must make reasonable assumptions on the constants in the model equations to establish the existence. This was missing in the old papers.One must establish the existence of f i nitely many points where the pulse crosses the threshold and find the intervals where the pulse lies above or below the threshold.One also has to prove that the pulse is continuously dif f erentiable everywhere on R,particularly at the points where the pulse crosses the threshold.However,they did not do these things.That is why the previous existence analysis is not rigorously correct.The existence of the standing pulse solutions may be proved by applying standard ideas,methods and techniques in dynamical systems to guarantee that all of the above requirements are valid.For the instability,there have been no rigorous mathematical analysis on the essential spectrum or the eigenvalues of some associated linear dif f erential operator obtained from the linearization of the nonlinear system of reaction dif f usion equations about the standing pulse solution.

2 Mathematical Analysis and Proofs of the Main Results

The main purpose of this section is to accomplish the existence and instability of the standing pulse solutions.We will couple together linearized stability criterion and Evans functions(complex analytic functions)to accomplish the nonlinear instability of the standing pulse solutions.

1.The Existence.First of all,let us establish the existence of the standing pulse solution to the nonlinear system of reaction dif f usion equations(1.1)-(1.2). A standing pulse solution to system(1.1)-(1.2)satisf i es the following dif f erential equations

That is

Suppose that there exists a positive constantZ＞0,such that

Then the above dif f erential equation reduces to

subject to the boundary conditionsU(0)=θandU(Z)=θ.Solving these dif f erential equations and using the boundary conditions lead to the solution representation

whereC1,C2andZare real unknown constants.Now let us find the constants. First of all,U(0)=θandU(Z)=θ,that is

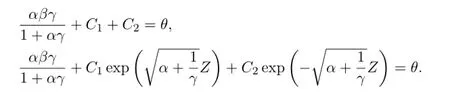
Second,the standing pulse solution is continuously dif f erentiable everywhere,particularly,atx=0 andx=Z.Hence

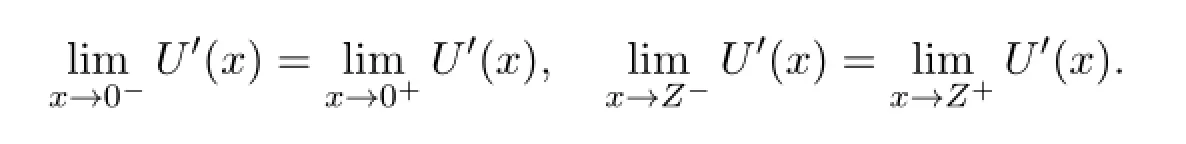
That is

Coupling all of these equations together yields

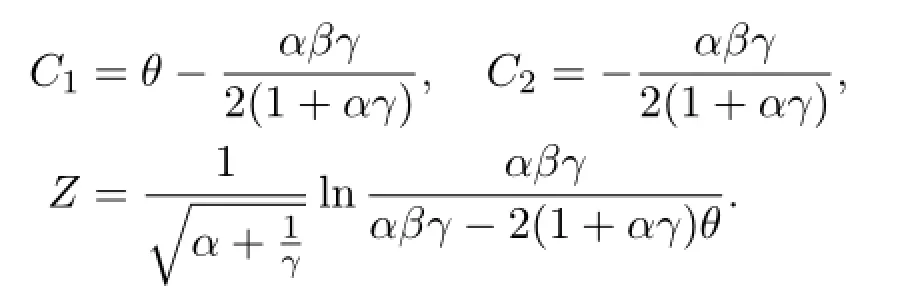
This completes the proof of the existence and uniqueness of the single standing pulse solution to system(1.1)-(1.2).A standing pulse solution to the nonlinear scalar reaction dif f usion equation(1.3)satisf i es the following dif f erential equation

The existence and uniqueness of the standing pulse solution to the nonlinear scalar reaction dif f usion equation(1.3)may be established very similarly.

Next let us study the instability of the standing pulse solution to the nonlinear system of reaction dif f usion equations(1.1)-(1.2).

2.The eigenvalue problems.Let(P(x,t),Q(x,t))=(u(x,t),w(x,t)).Then (1.1)-(1.2)becomes

The standing pulse solution(U,W)=(U(x),W(x))is a stationary solution to this system.Linearizing the nonlinear system about the standing pulse solution to get

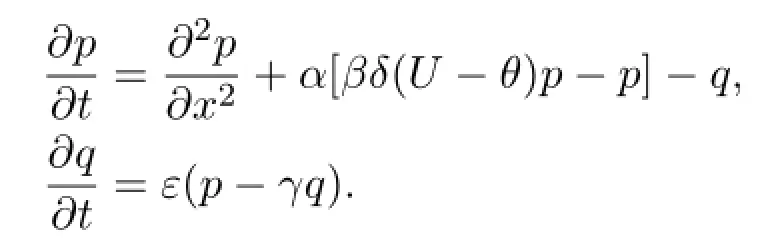
Suppose that(p(x,t),q(x,t))=exp(λt)(ψ1(x),ψ2(x))is a complex solution to this linear system of dif f erential equations,whereλis a complex number,ψ1andψ2are complex,bounded,continuous functions def i ned on R.This leads to the following eigenvalue problem

Def i ne a linear dif f erential operatorLby

To see thatλ0=0 is an eigenvalue and(ψ1(x),ψ2(x))=(U′(x),W′(x))is an eigenfunction of the eigenvalue problem,let us dif f erentiate the standing pulse equations

with respect toxto get

Def i nition 2(I)The standing pulse solution to the nonlinear system of reaction dif f usion equations(1.1)-(1.2)is stable,if max{Reλ:λ∈σ(L)0}≤-C0andλ0=0 is an algebraically simple eigenvalue,whereσ(L)represents the spectrum of the linear dif f erential operatorLandC0＞0 is a positive constant.

(II)The standing pulse solution to the nonlinear system of reaction dif f usion equations(1.1)-(1.2)is unstable,if there exists an eigenvalueλ0with positive real part or if the neutral eigenvalueλ0=0 is not simple.

Following John Evans’idea in[2],the essential spectrum of the linear dif f erential operatorLis easy to find and it is given by

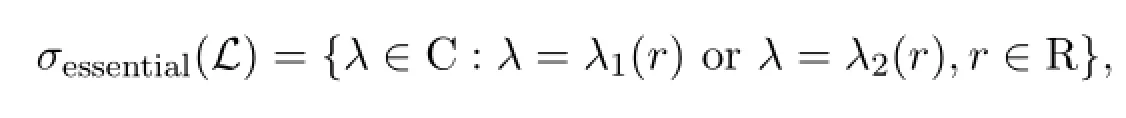
where

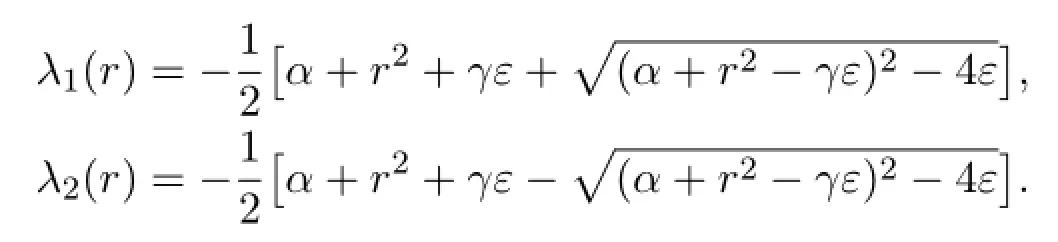
It is easy to find that the essential spectrum ofLcauses no problem to the stability of the standing pulse solution to the nonlinear system of reaction dif f usion equations (1.1)-(1.2).

Let us find a simpler equation which is equivalent to the eigenvalue problemλψ1=1-ψ2+αβδ(U-θ)ψ1,λψ2=ε(ψ1-γψ2),so that we can solve it to find a solution to the eigenvalue problem.Recall that the standing pulse solution satisf i es the conditions:U(0)=θ,U′(0)＞0,U(Z0)=θ,U′(Z0)＜0,U＞θon (0,Z0)andU＜θon(-∞,0)∪(Z0,∞).Thus

everywhere on R.Dif f erentiating this equation with respect toxyields

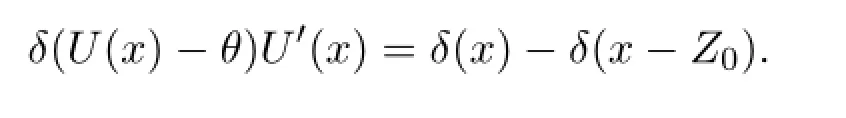
That is

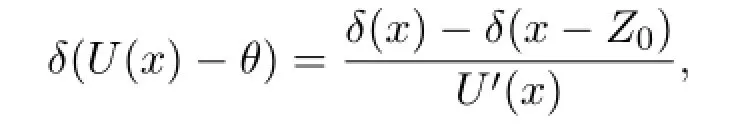
for allxsuch thatU′(x)0.Moreover,we have

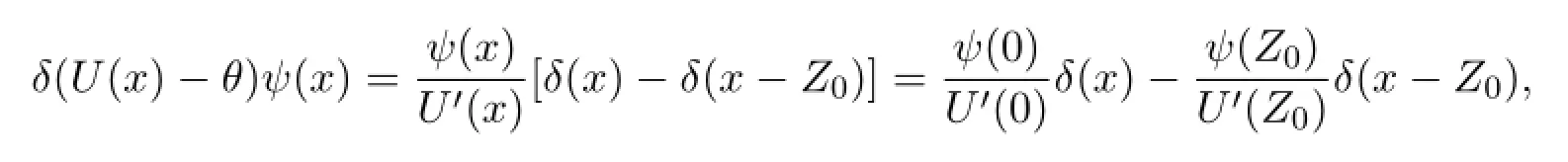
for all complex valued functionsψdef i ned on R,in the sense of tempered distributions.Therefore,if we writeψ1=ψand use the relationship,then the eigenvalue problemλψ1=1-ψ2+αβδ(U(x)-θ)ψ1,λψ2=ε(ψ1-γψ2) becomes

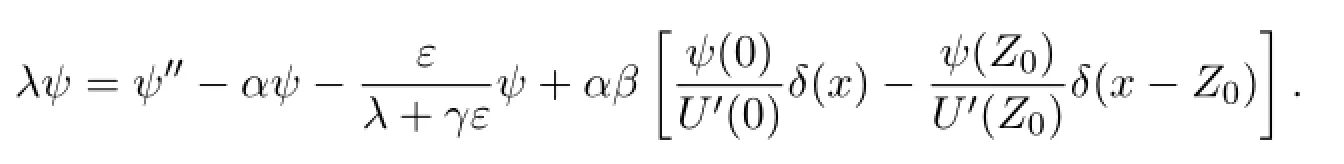
3.The solutions of the eigenvalue problems.Def i ne Ω={λ∈C:Reλ＞-γε}.The eigenvalue problem may be written as a nonhomogeneous,f i rst order, linear system of dif f erential equations

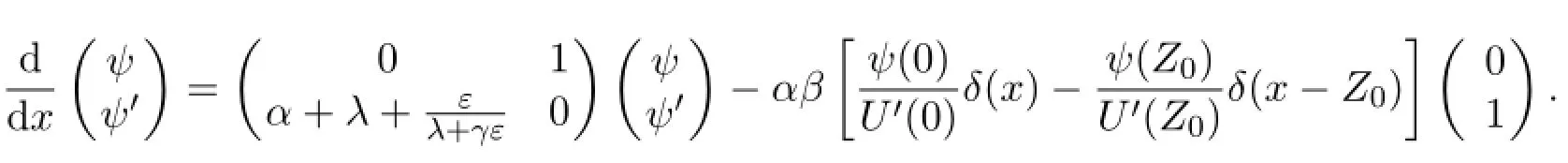
For all complex numbersλwith Reλ＞-γε,the solution of the homogeneous system

厨房食物垃圾中含有大量易腐物质，现有的垃圾收集器和运输车辆对其并不适宜，因餐厨垃圾含水量比较高，用密封瓶装搬运很费劲、稍有不慎会导致废液体从瓶里溢出来；用密封罐车装运，上卸很麻烦，在运输工程中假如道路不平整会产生颠簸，废液有时从缝隙处渗漏出来；集中堆放点处理不当，废液会渗透到附近土壤里去，污染周边的水源和地下水，从而带来新的二次污染。

is given by

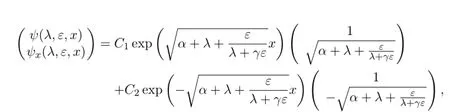
whereC1andC2are constants.

Let us diagonalize the coefficient matrix.Def i ne

Then the inverse matrix exists and it is given by

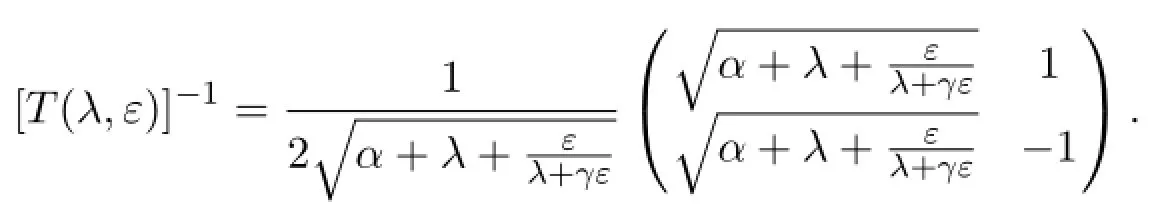
Therefore

Clearly

are two fundamental matrices of the homogeneous system.

Let us use the method of variation of parameters and the two fundamental matrices to find a bounded particular solution.The particular solution to the nonhomogeneous system is given by

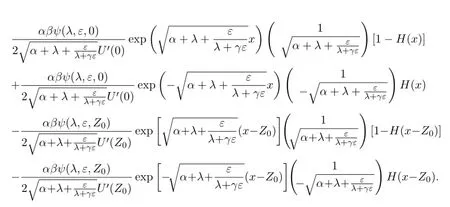
Therefore,the general solution to the eigenvalue problem is given by

whereC1(λ,ε)andC2(λ,ε)are independent ofx,but depend on the parametersλandε.The general solution to the eigenvalue problem is bounded on R if and only if

The f i rst component of the general solution to the eigenvalue problem is given by

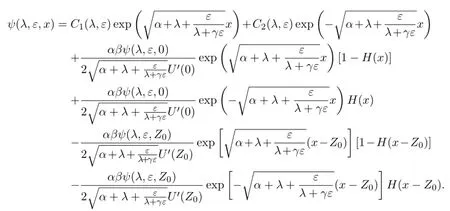
These equations may be written in another way

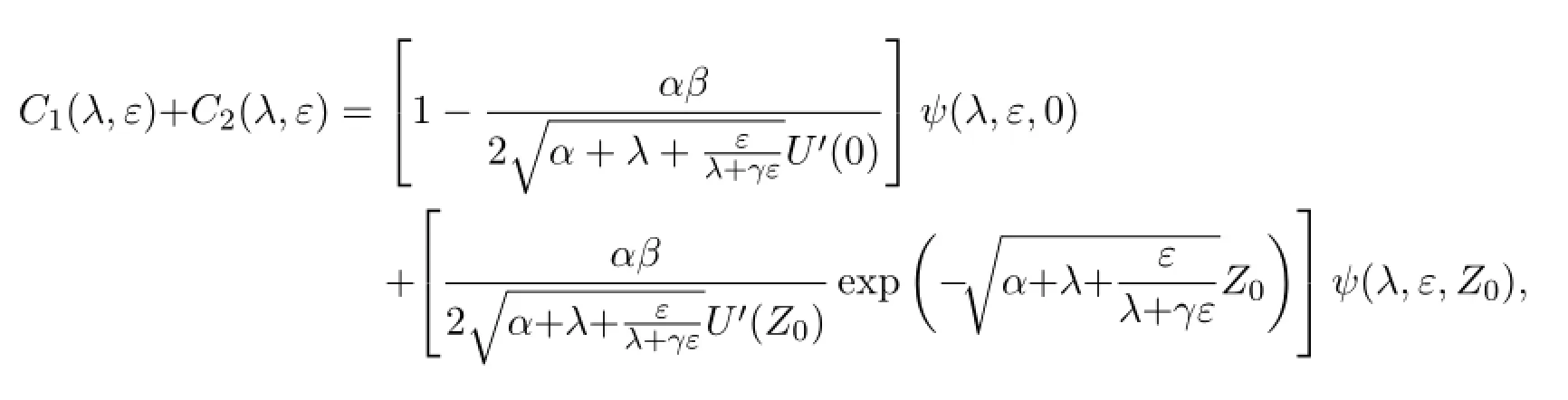
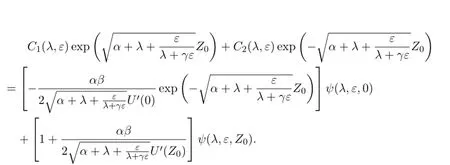
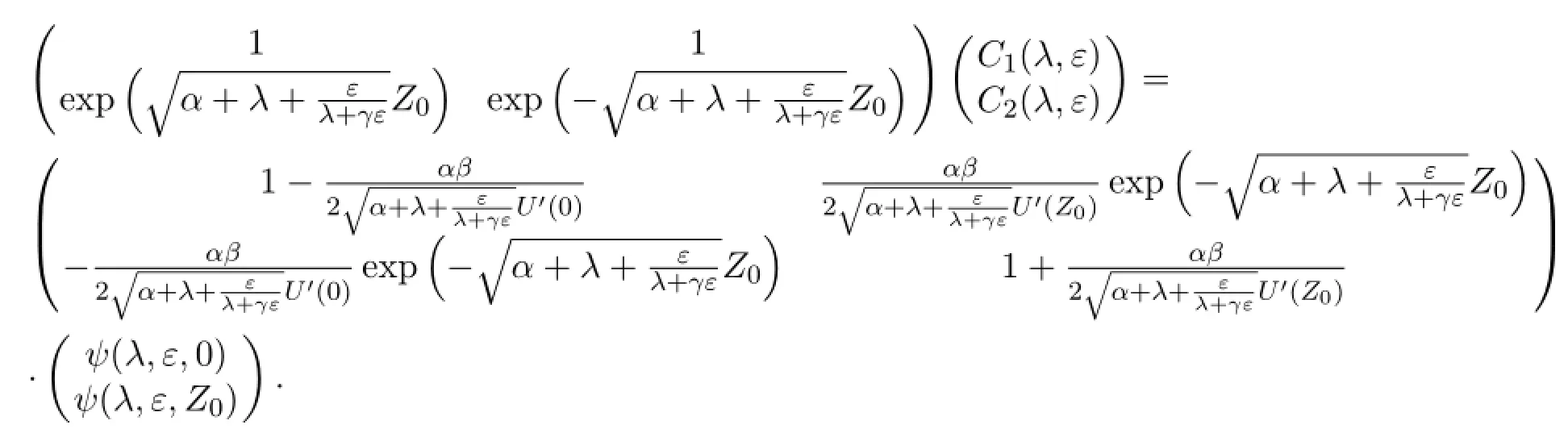
4.The Evans function and its representation.Def i ne the Evans function for the standing pulse solution to the nonlinear system of reaction dif f usion equations

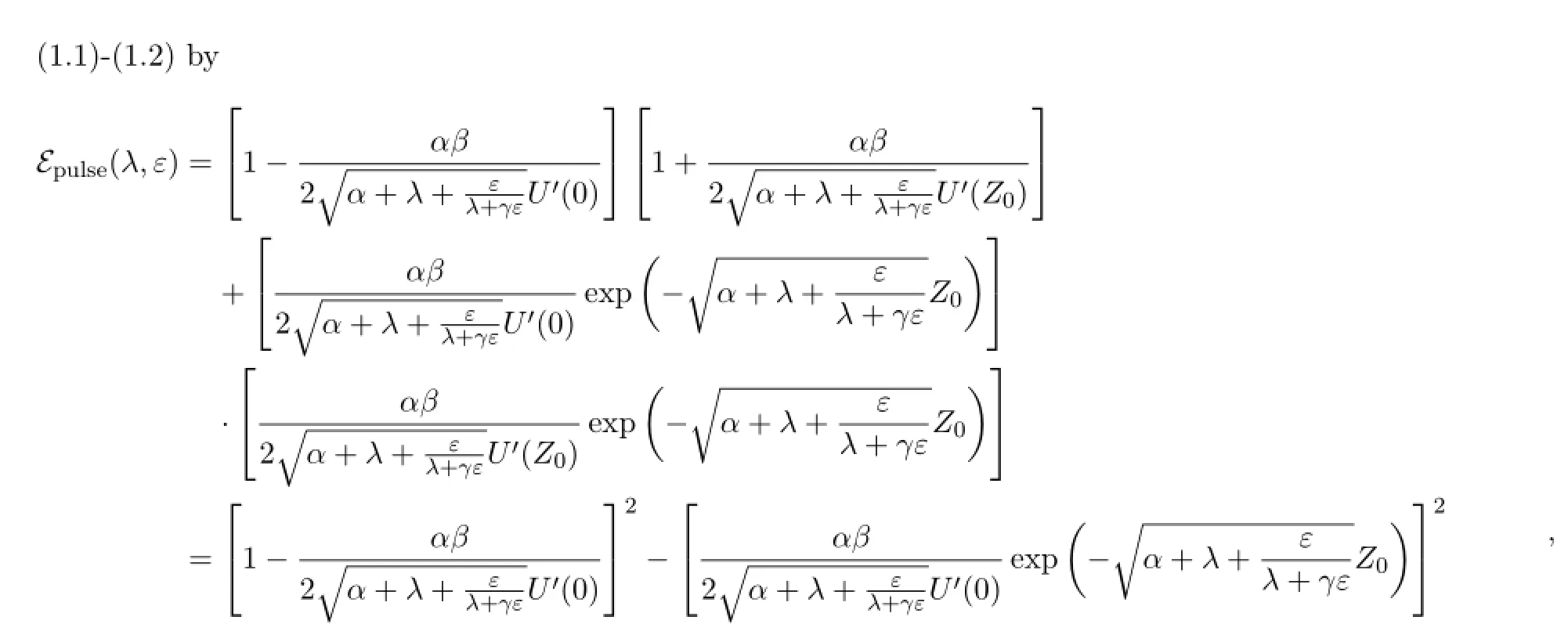
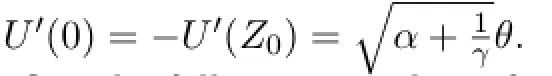
Def i ne the following auxiliary functions

Then

Recall that

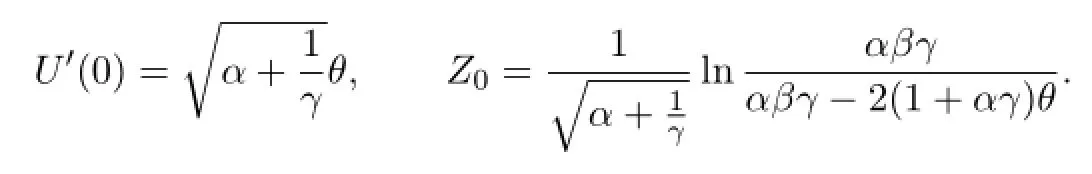
First of all,we have

Then we have the derivatives

and

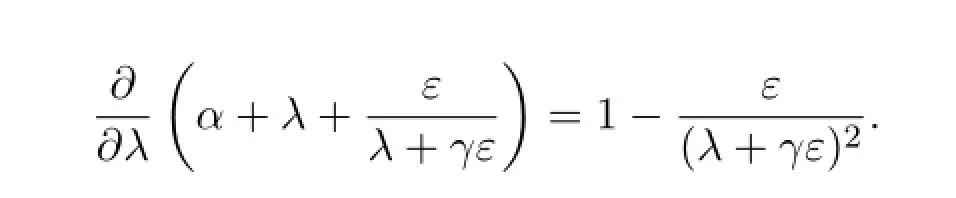
There is a critical numberObviously,λc＜0 ifγ2ε＞1 andλc＞0 if 0＜γ2ε＜1.

Let us study the zeros of the Evans function.It is easy to find that

if and only ifF(λ,ε)=1 orG(λ,ε)=1,that isλ=0 orλ=λ0(ε),whereλ0(ε)is the unique solution of the equation

Note that

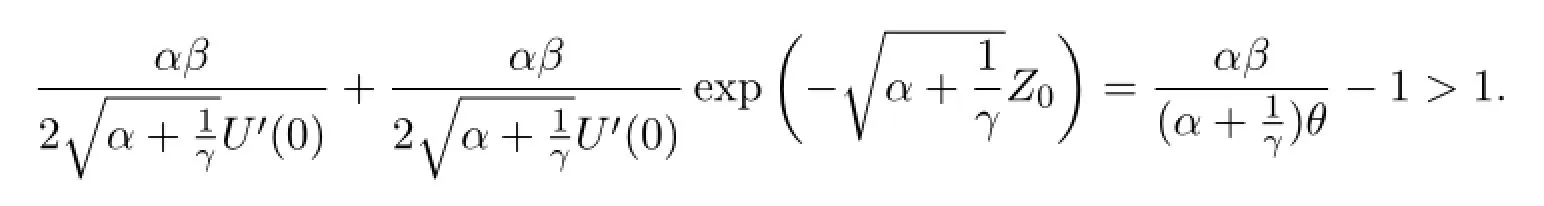
The existence and uniqueness of such a real solutionλ0(ε)may be proved by using intermediate value theorem and mean value theorem.Letγ2ε＞1.Then-γε＜λ0(ε)＜0.Let 0＜γ2ε＜1.Thenλ0(ε)＞0.

5.The stability/instability of the standing pulse solutions.The linearized stability criterion:The nonlinear stability of the standing pulse solution to the nonlinear system of reaction dif f usion equations(1.1)-(1.2)is equivalent to its linear stability,which is equivalent to the spectral stability.

By using the def i nitions of the stability and instability of the standing pulse solution to the nonlinear system of reaction dif f usion equations(1.1)-(1.2)and by using the linearized stability criterion,we find that the standing pulse solution is unstable.

6. The instability of the standing pulse solution to the nonlinear scalar reaction dif f usion equation(1.3).For the standing pulse solution to the nonlinear scalar reaction dif f usion equation

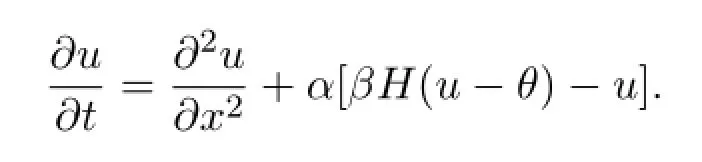
the eigenvalue problem is

The linear dif f erential operatorL0is def i ned by

The essential spectrum of the operatorL0is

The eigenvalue problem may be rewritten as

The general solution is given by

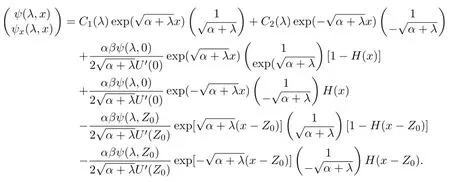
The f i rst component of the general solution is given by

The Evans function is def i ned by

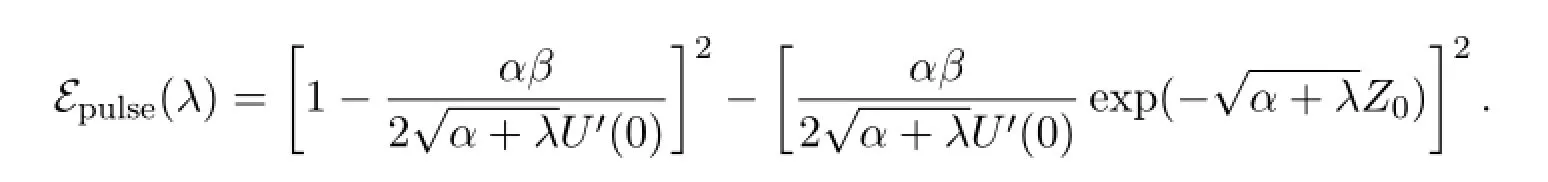
There exists a positive eigenvalueλ0＞0.The instability of the standing pulse solution to the nonlinear scalar reaction dif f usion equation(1.3)is established.The proof of Theorem 1 is f i nished.

3 Conclusion and Remarks

3.1 Summary

Consider the following nonlinear system of reaction dif f usion equations arising from mathematical neuroscience

and the nonlinear scalar reaction dif f usion equations

and

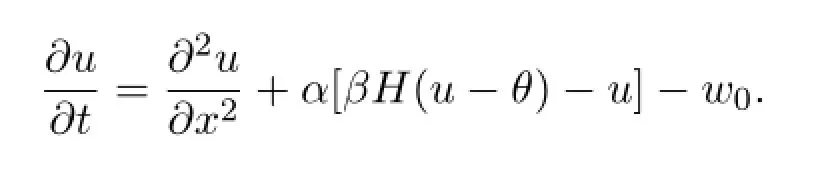
The main purpose is to couple together the linearized stability criterion(the equivalence of the nonlinear stability,the linear stability and the spectral stability of the standing pulse solutions)and Evans functions to accomplish the nonlinear instability of the standing pulse solutions.We constructe Evans functions(complex analytic functions)to accomplish the instability of the standing pulse solutions.We study the eigenvalues and eigenfunctions of some eigenvalue problems.It turns out that a complex numberλ0is an eigenvalue of the eigenvalue problem if and only ifλ0is a zero of the Evans function.The introduction and application of the Evans functions to standing pulse solutions to the model equations will have great impacts on how to construct and apply Evans functions for stability of fast multiple traveling pulse solutions.

The scalar equations may be obtained by settingε=0 andw=0,ε=0 andw0=α(β-2θ),respectively,in the system.

Summary of the eigenvalue problem

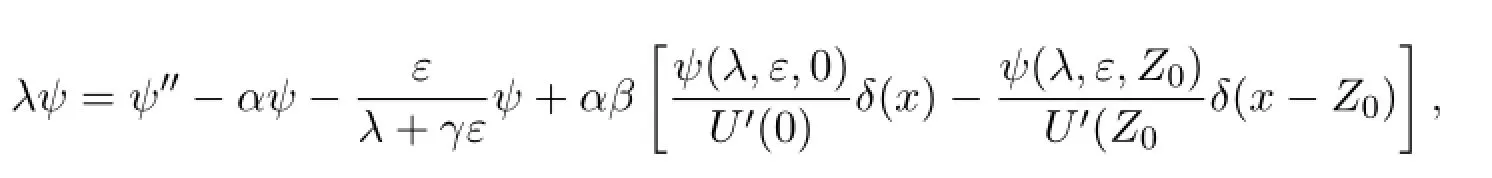
and the Evans function

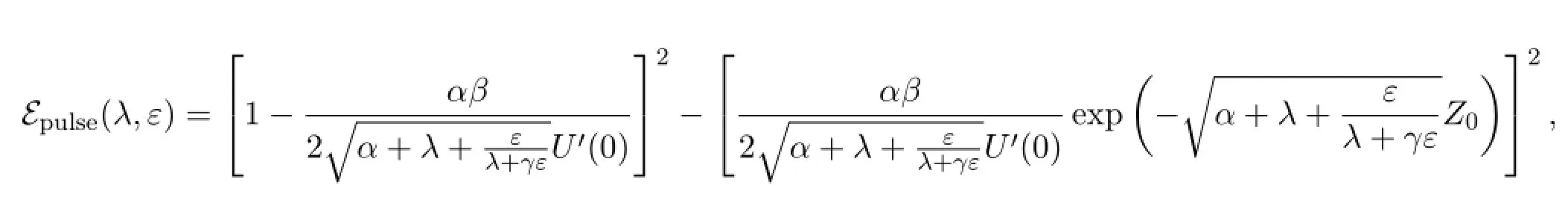
for the nonlinear system of reaction dif f usion equations

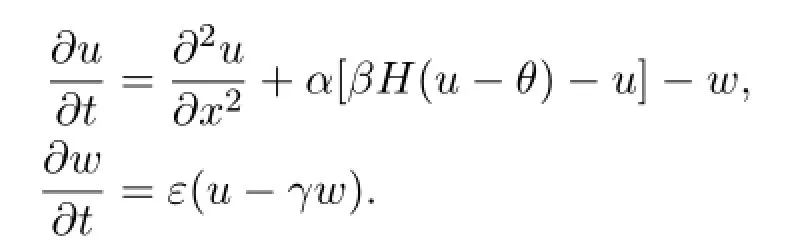
(I)The Evans functionE=Epulse(λ,ε)is a complex analytic function ofλandε,it is real-valued ifλis real.

(II)The complex numberλ0is an eigenvalue of the eigenvalue problem if and only ifλ0is a zero of the Evans function,that is,Epulse(λ0,ε)=0.In particular,Epulse(0,ε)=0.

(III)The imaginary part of the Evans functionEpulse(λ,ε)is equal to zero if and only if the imaginary part ofλis equal to zero.In another word,all eigenvalues to the eigenvalue problem are real.

(IV)The algebraic multiplicity of any eigenvalueλ0of the eigenvalue problem is equal to the order of the zeroλ0of the Evans functionE=E(λ,ε).

(V)The Evans function enjoys the following limit

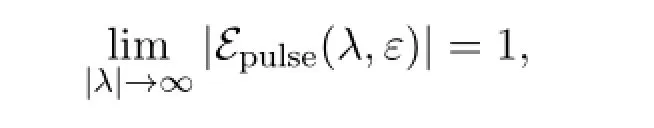
in the right half plane{λ∈C:Reλ＞-γε}.

3.2 Future Directions and Open Problems

Consider the following nonlinear singularly perturbed system of reaction dif f usion equations(1.1)-(1.2),that is

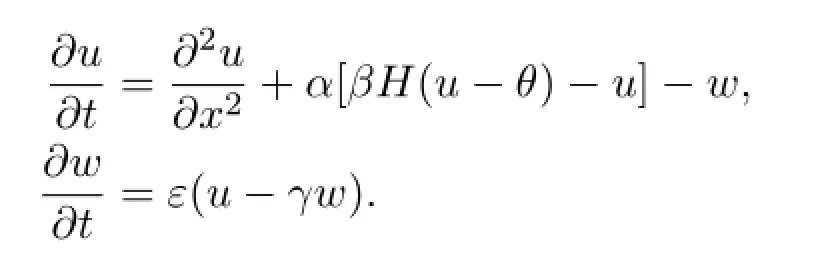
In the future,we would like to accomplish the existence and stability of fast multiple traveling pulse solutions

with fast moving coordinatesz=x+νfast(ε)tand fast wave speedsνfast(ε),and to accomplish the existence and instability of slow multiple traveling pulse solutions

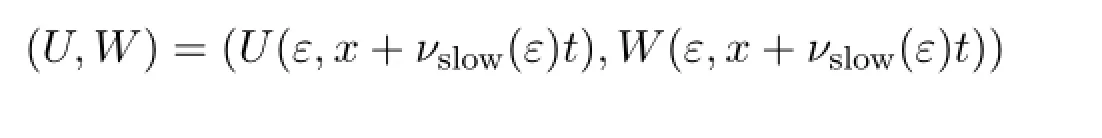
with slow moving coordinatesz=x+νslow(ε)tand slow wave speedsνslow(ε).These problems are very interesting and important in applied mathematics but they have been open for a long time.We will introduce Evans functions and establish a global strong maximum principle for Evans functions,couple together linearized stability criterion,Hopf lemma and many other important ideas,methods and techniques in dynamical systems to accomplish the existence and stability of the fast multiple traveling pulse solutions.

Consider the nonlinear scalar reaction dif f usion equation

There exists a unique stable traveling wave frontu(x,t)=Ufront(x+ν0t),such thatU∈C1(R)∩C2(R-{0});U＜θon(-∞,0),U(0)=θ,U′(0)＞0 andU＞θon (0,∞).The wave speedν0is given by

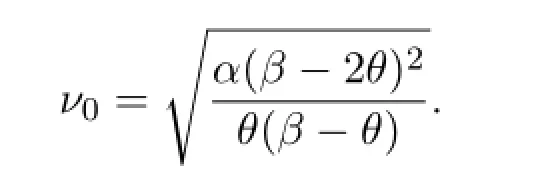
Letz=x+ν0t.The traveling wave front is given explicitly by

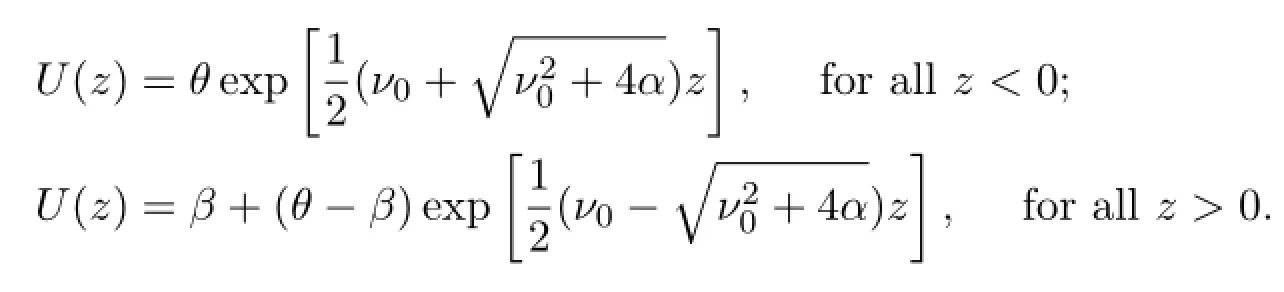
The traveling wave front enjoys the following boundary conditions

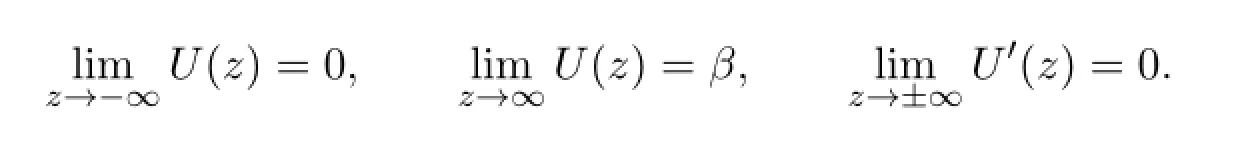
Consider the nonlinear scalar reaction dif f usion equation

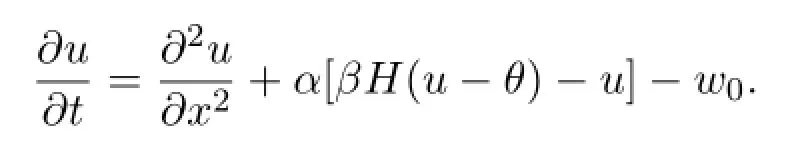
There exists a unique stable traveling wave backu(x,t)=Uback(x+ν0t),such thatU∈C1(R)∩C2(R-{0});U＞θon(-∞,0),U(0)=θ,U′(0)＜0 andU＜θon (0,∞).Letz=x+ν0t.The traveling wave back is given explicitly by

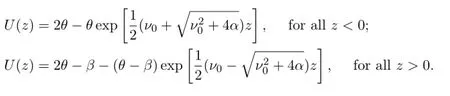
The traveling wave back enjoys the following boundary conditions

Under the same assumptionsα＞0 and 0＜2θ＜β,the nonlinear scalar reaction dif f usion equation(1.3)supports both a traveling wave front and a standing pulse solution.When the parameterεis perturbed fromε=0 toε＞0,the traveling wave front becomes part of the fast traveling pulse solution and the standing pulse solution becomes part of the slow traveling pulse solutions.

3.3 Remarks

The fast single traveling pulse solution may be viewed as the perturbation of the traveling wave front and the traveling wave back.The fast multiple traveling pulse solution may be viewed asmcopies of the fast single traveling pulse solution appropriately placed together.Therefore,the Evans function for the fast single traveling pulse solution is equal to the product of the Evans function for the traveling wave front and the Evans function for the traveling wave back plus a small function due to perturbation.The Evans function for the fast multiple traveling pulse solution is equal to the product ofmEvans functions for the fast single traveling pulse solution plus a small function due to perturbation.More precisely

for allλ∈Ω andε＞0,where Ω={λ∈C:Reλ＞-γε}is a right half complex plane.

Very similarly,for slow single traveling pulse solution and slow multiple traveling pulse solutions,there hold the following representations for the Evans functions

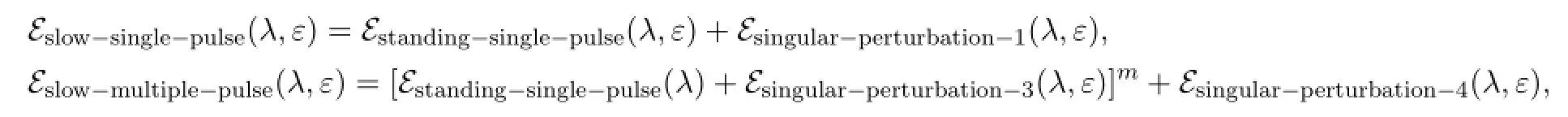
for allλ∈C with Reλ＞-γεand for allε＞0,where

To see if the neutral eigenvalue is algebraically simple,let us dif f erentiate the representations with respect toλ.We have

Letλ=0,then we have

Overall,the neutral eigenvalueλ=0 is simple.

3.4 A Technical Lemma

LemmaLet A be an(2m)×(2m)complex constant matrix.Suppose that Aηk=µkηk,that is,µ1,µ2,···,µ2mare the eigenvalues and η1,η2,···,η2mare the corresponding linearly independent eigenvectors of A.The real parts of the eigenvalues satisfy Reµk＞0,for all k=1,2,···,p andReµk＜0,for all k=p+1,···,2m,for some positive integer p≥1.Let δ represent the Dirac delta impulse function.Let x1,x2,x3,···,x2mbe real constants and ξ1,ξ2,ξ3,···, ξ2mbe complex constant vectors.Consider the following linear system of dif f erential equations

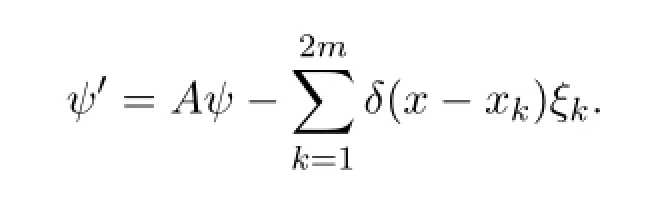
There exists a bounded explicit particular solution to the system

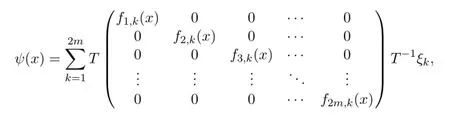
where T=(η1,η2,···,η2m)is the matrix consisting of the linearly independent eigenvectors,and

for all k=1,2,···,p and

for all k=p+1,···,2m,where H=H(x-xk)is a Heaviside step function,def i nedby H(x-xk)=0on(-∞,xk),H(0)=,H(x-xk)=1on(xk,∞).

Proof Note that

is a fundamental matrix of the homogeneous linear systemψ′=Aψ,for allk= 1,2,3,···,2m.By using the method of variation of parameters and the fundamental matrices,the proof is very easy and it is omitted.

[1]John W.Evans,Nerve axon equations,I Linear approximations,Indiana University Mathematics Journal,21(1971),877-885.

[2]John W.Evans,Nerve axon equations,II Stability at rest,Indiana University Mathematics Journal,22(1972),75-90.

[3]John W.Evans,Nerve axon equations,III Stability of the nerve impulse,Indiana University Mathematics Journal,22(1972),577-593.

[4]John W.Evans,Nerve axon equations,IV The stable and the unstable impulse,Indiana University Mathematics Journal,24(1975),1169-1190.

[5]John A.Feroe,Traveling waves of inf i nitely many pulses in nerve equations,Mathematical Biosciences,55(1981),189-203.

[6]John A.Feroe,Existence and stability of multiple impulse solutions of a nerve equation,SIAM Journal on Applied Mathematics,42(1982),235-246.

[7]John A.Feroe,Existence of traveling wave trains in nerve axon equations,SIAM Journal on Applied Mathematics,46(1986),1079-1097.

[8]Henry P.McKean,Nagumo’s equation,Advances in Mathematics,4(1970),209-223.

[9]Henry P.McKean,Stabilization of solutions of a caricature of the Fitzhugh-Nagumo equation,Communications in Pure and Applied Mathematics,36(1983),291-324.

[10]Henry P.McKean,Stabilization of solutions of a caricature of the Fitzhugh-Nagumo equation.II,Communications in Pure and Applied Mathematics,37(1984),299-301.

[11]Henry P.McKean and Victor Moll,Stabilization to the standing wave in a simple caricature of the nerve equation,Communications in Pure and Applied Mathematics, 39(1986),485-529.

[12]John Rinzel and Joseph B.Keller,Traveling wave solutions of a nerve conduction equation,Biophysical Journal,13(1973),1313-1337.

[13]John Rinzel and David Terman,Propagation phenomena in a bistable reaction-dif f usion system,SIAM Journal on Applied Mathematics,42(1982),1111-1137.

[14]David Terman,Threshold phenomena for a reaction-dif f usion system,Journal of Differential Equations,47(1983),406-443.

[15]Wei-Ping Wang,Multiple impulse solutions to McKean’s caricature of the nerve equation.I.Existence,Communications on Pure and Applied Mathematics,41(1988),71-103.

[16]Wei-Ping Wang,Multiple impulse solutions to McKean’s caricature of the nerve equation.II.Stability,Communications on Pure and Applied Mathematics,41(1988),997-1025.

(edited by Liangwei Huang)

∗This project was partly supported by a Faculty Research Grant of Lehigh University.

†Manuscript received

‡Corresponding author.E-mail:liz5@lehigh.edu.

The main purpose is to couple together linearized stability criterion(the equivalence of the nonlinear stability,the linear stability and the spectral stability of the standing pulse solutions)and Evans functions to accomplish the existence and instability of standing pulse solutions of the nonlinear system of reaction dif f usion equations and the nonlinear scalar reaction dif f usion equations.The Evans functions for the standing pulse solutions are constructed explicitly.