CYCLES EMBEDDING ON FOLDED HYPERCUBES WITH FAULTY NODES∗†

Dan Yuan,Hongmei Liu,Maozheng Tang

(College of Science,Three Gorges University,Hubei 443002,PR China)

CYCLES EMBEDDING ON FOLDED HYPERCUBES WITH FAULTY NODES∗†

Dan Yuan‡,Hongmei Liu,Maozheng Tang

(College of Science,Three Gorges University,Hubei 443002,PR China)

LetFFvbe the set of faulty nodes in ann-dimensional folded hypercubeFQnwith|FFv|≤n-1 and all faulty vertices are not adjacent to the same vertex.In this paper,we show that ifn≥4,then every edge ofFQn-FFvlies on a fault-free cycle of every even length from 6 to 2n-2|FFv|.

folded hypercube;interconnection network;fault-tolerant; path

2000 Mathematics Subject Classification

1 Introduction

Then-dimensional hypercubeQn(orn-cube)is one of the most important topology of networks due to its excellent properties such as regularity,recursive structure, small diameter,vertex and edge transitive and relatively short mean distance[1]. In order to improve the performance of hypercube,the folded hypercubeFQnhas been proposed[2].

Since a large-scale hypercube network,fails in any component,it’s desirable that the rest of the network continue to operate in spite of the failure.This leads to the graph-embedding problem with faulty edges and/or vertices.This problem has received much attention(see[3-10]).

The problem of embedding paths in ann-dimensional hypercube and folded hypercube has been well studied.Tsai[3]showed that for any subsetFvofV(Qn) with|Fv|≤n-2,every edge ofQn-Fvlies on a cycle of every even length from 4 to 2n-2|Fv|inclusive.Tsai[4]also showed that for any subsetFvofV(Qn)with|Fv|≤n-1 and all faulty vertices are not adjacent to the same vertex,every edge ofQn-Fvlies on a cycle of every even length from 6 to 2n-2|Fv|inclusive.Hsiehand Shen[5]proved that every edge ofQn-Fv-Felies on a cycle of every even length from 4 to 2n-2|Fv|even if|Fv|+|Fe|≤n-2,wheren≥3.

LetFFvandFFedenote the set of faulty nodes and faulty edges ofFQnrespectively.Hsieh,Kuo and Huang[6]proved that if the folded hypercubeFQnhas just only one fault node,thenFQncontains cycles of every even length from 4 to 2n-2 ifn≥3,and cycles of every odd length fromn+1 to 2n-1 whennis even,n≥2.Ma, Xu and Du[7]further demonstrated thatFQn-FFe(n≥3)with|FFe|≤2n-3 contains a fault-free cycle passing through all nodes if each vertex is incident with at least two fault-free edges.Kuo and Hsieh[8]improved the conclusion of[7]and proved thatFQn-FFewith|FFe|=2n-3 contains a fault-free cycle of every even length from 4 to 2n.Xu,Ma and Du[9]further showed that every fault-free edge ofFQn-FFelies on a fault-free cycle of every even length from 4 to 2nand every odd length fromn+1 to 2n-1 ifnis even,where|FFe|≤n-1.Then Cheng,Hao and Feng[10]proved that every fault-free edge ofFQn-FFvlies on a fault-free cycle of every even length from 4 to 2n-2|FFv|and every odd length fromn+1 to 2n-2|FFv|-1 ifnis even,where|FFv|≤n-2.

In this paper,under the conditional|FFv|≤n-1 and all faulty vertices are not adjacent to the same vertex,we show that ifn≥4,then every edge ofFQn-FFvlies on a fault-free cycle of every even length from 6 to 2n-2|FFv|.

2 Preliminaries

Please see[1]for graph-theoretical terminology and notation is not def i ned here. A network is usually modeled by a simple connected graphG=(V,E),whereV=V(G)(orE=E(G))is the set of vertices(or edges)ofG.We def i ne the vertexxto be a neighbor ofyifxy∈E(G).A graphGis bipartite ifX,Yare two disjoint subsets ofV(G)such thatE(G)={xy|x∈X,y∈Y}.A graphP=(u1,u2,···,uk) is called a path if the verticesu1,u2,···,ukare distinct and any two consecutive verticesuiandui+1are adjacent.u1andukare called the end-vertices ofP.Ifu1=uk,the pathP(u1,uk)is called a cycle(denoted byC).The length of a pathP(a cycleC),denoted byl(P)(orl(C)),is the number of edges inP(orC).In general,the distance of two verticesx,yis the length of the shortest(x,y)-path.

Then-dimensional hypercubeQn(or,n-cube)can be represented as an undirected graph with 2nvertices.Every vertexx∈Qnis labeled as a binary stringx1x2···xnof lengthnfrom 00···0 to 11···1.Two verticesuandvare adjacent if their binary strings dif f er in exactly one bit.For convenience,we calle∈Ean edge of dimensioniif its end-vertices strings dif f er inith-bit.In the rest of this paper,we denote,where=1-xi,xi=0,1.The Hammingdistance of two verticesx=x1x2···xnandy=y1y2···ynisH(x,y)the number of dif f erent bits between them.LetdH(x,y)be the shortest distance ofxandy.Note thatQnis a bipartite graph,and for any two distinct verticesx,yofQn,dH(x,y)=H(x,y).N(x)denotes a set of the nodes which are neighbors ofx.

As a variant of hypercube,then-dimensional folded hypercubeFQnis obtained by adding more edges between its vertices.

Def i nition 1 Then-dimensional folded hypercubeFQnis a graph withV(Qn)=V(FQn).Two verticesx=x1x2···xnandyare connected by an edge if and only if

Therefore,the hypercubeQnis a spanning subgraph of the folded hypercubeFQnobtained by removing the second type of edges(x∈V(FQn)),called complementary edges ofFQnand denoted by

In general,the f i rst type of edges are def i ned to be the hypercube edges,and denoted byEi={xxi},i=1,2,···,n.

Lemma 1An i-partition on FQn,where1≤i≤n,is a partition of FQnalong dimension i into two n-1-cubes,denoted byand.

()can also be denoted by0x(respectively,1x)for brevity,where satisfying0x=x1x2···xi···xn∈satisfying xi=0 (respectively,1x=x1x2···xi···xn∈satisfying xi=1).

Lemma 2[4]Let fe=0,fv=n-1,and every fault-free vertex is adjacent to at least two fault-free vertices in Qnfor n≥4.Then,every fault-free edge of Qnlies on a fault-free cycle of every even length from 6 to2n-2fvinclusive.

Lemma 3[3]Assume Fvis any subset of V(Qn).Every edge in Qn-Fvlies on a fault-free cycle of every even length from4to2n-2fvinclusive even if|Fv|≤n-2, where n≥3.

Lemma 4[12]Let n≥2be an integer.For any two dif f erent fault-free vertices u and v in Qnwith fe+fv≤n-2,there exists a fault-free uv-path of length l for each l satisfying dH(u,v)+2≤l≤2n-2fv-1and2|(l-dH(u,v)).Moreover, there must exist a fault-free uv-path of length dH(u,v)if dH(u,v)≥n-1.

Lemma 5[10]Assume that FQnis partitioned along dimension i(1≤i≤n)into two n-1-cubes,denoted byand,0u and0v(respectively,1u and1v)().If dH(0u,0v)=n-2(respectively,dH(1u,1v)=n-2),then dH(,1v)=1and dH(1u,)=1 (respectively,dH(,0v)=1and dH(0u,)=1);if dH(0u,0v)=1(respectively, dH(1u,1v)=1),then dH(,1v)=n-2and dH(1u,)=n-2(respectively,dH(,0v)=n-2and dH(0u,)=n-2).

Lemma 6[5]There exists a path of every odd length from 3 to2n-2|Fv|-1joining any two adjacent fault-free nodes in Qn-Fveven if|Fe|=0and|Fv|≤n-2, where n≥3.

Lemma 7[10]Assume n is even and FFvis any subset of V(FQn).Every edge of FQn-FFvlies on a fault-free cycle of every odd length from n+1to2n-2|FFv|-1inclusive even if|FFv|≤n-2,where n≥2.

Lemma 8Assume that FQnis partitioned along dimension i(1≤i≤n)into two n-1-cubes,denoted byand,0u and0v(respectively,1u and1v)().If dH(0u,0v)=n-3(respectively,dH(1u,1v)=n-3),then dH(,1v)=2and dH(1u,)=2(respectively,dH(,0v)= 2and dH(0u,)=2);if dH(0u,0v)=2(respectively,dH(1u,1v)=2),then dH(,1v)=n-3and dH(1u,)=n-3(respectively,dH(,0v)=n-3and dH(0u,)=n-3).

Proof IfdH(0u,0v)=n-3,thendH(u,v)=n-3,which impliesdH=2 anddH()=2,thusdH(,1v)=2 anddH(1u,)=2.By the similar discussion, ifdH(1u,1v)=n-3,thendH(,0v)=2 anddH(0u,)=2.

IfdH(0u,0v)=2,thendH(u,v)=2,which impliesdH()=n-3 anddH()=n-3,thusdH(,1v)=n-3 anddH(1u,)=n-3.By the similar discussion,ifdH(1u,1v)=2,thendH(,0v)=n-3 anddH(0u,)=n-3.The proof is completed.

Lemma 9[2]For any two vertices u,v∈Qn,if d(u,v)=k,then there are n internal disjoint paths from u and v such that there are k paths of length k and n-k paths of length k+2.

Lemma 10[10]Assume FFvis any subset of V(FQn).Every edge in FQn-FFvlies on a fault-free cycle of every even length from 4 to2n-2|FFv|inclusive even if |FFv|≤n-2,where n≥3.

Lemma 11[9]There is an automorphism σ of FQnsuch that σ(Ei)=Ejfor any i,j∈{1,2,···,n,c}.

3 Main Results

Before the proof,I give some symbols.FFvis the set of faulty vertices inFQnandis the set of faulty vertices in,i={0,1}.

Lemma 12Assume FFvis any subset of V(FQ4).Every edge in FQ4-FFvlies on a fault-free cycle of every even length from 6 to24-2|FFv|inclusive even if |FFv|≤3and all faulty vertices are not adjacent to the same vertex.

Proof If|FFv|=fv≤2,by Lemma 10,the lemma holds.Therefore,we only need to consider the situation offv=3,every edge inFQ4-FFvlies on a fault-free cycle of every even length from 6 to 10 inclusive.By Lemma 1,FQ4can be partitioned along dimensioniinto two 3-cubes,denoted byand.There must exist anisuch that(u),and(v),(We can simply divide one of the faulty vertex and the other faulty vertices into di ff erent partsor)along ani-dimension.The proof is the condition that all faulty vertices are not adjacent to the same vertex.We can consider extreme situation.Ifn-2 faulty vertices are adjacent to the same vertexx,we can choose one ofn-2 faulty vertices, denoted byy,thenxandyhave one bit dif f erently.So we can partition along this dimension.Thereforeyis in a part,other faulty vertices is in another part and all faulty vertices are not adjacent to the same vertex in this part).

Let=,i=0,1,.Without loss of generality, letFFv={w1,w2,w3},={w1,w2,={w3.=2,=1.eis a fault-free edge.=2,(u),,sodH(w1,w2)=1 ordH(w1,w2)=3.

(1).

Then,e∈C4,that is there exists a cycleC0of every even lengthl0containingein,wherel0=4.Let(x,y)/ebe a fault-free edge in cycleC0such that (xi,yi)(or)is fault-free in.LetC0=〈x,P0,y,x〉,then=l(P0)=3. Since=1,by Lemma 4,there exists a pathP1of every odd lengthl1joiningxiandyi(orand)in,where 3≤l1≤5.(xi,yi)(or)is fault-free,there exists a pathof every odd length joiningxiandyi(orand)in,where 15.LetC=〈x,P0,y,yi,xi,x〉orC=〈x,P0with even length.Since=3 and 15,6≤l≤10.

Through observation,e∈C6.Let(x,y)be a fault-free edge in cycleC0such that(xi,yi)(or)is fault-free in.LetC0=〈x,P0,y,x〉,then=l(P0),=5.Since=1,by Lemma 4,there exists a pathP1of every odd lengthl1joiningxiandyi(orand)in,where 3≤l1≤5.(xi,yi)(or)is fault-free,there exists a pathof every odd length joiningxiandyi(orand) in,where.LetC=〈x,P0,y,yi,xi,x〉orC=〈x,P0with even length.Sinceand,8≤l≤12.We can obtain the desired even cycle of length 6 inC0,wherel0=6.So 6≤l≤12.

(2)

Since=1,by Lemma 3,there exists a cycleC1of every even lengthl1containingein,where 4≤l1≤6.Let(x,y)be a fault-free edge in cycleC1such that(xi,yi)(or)is fault-free in.Hence,there exists a pathP1ofevery odd lengthjoiningxandyin,where.We can choose(xi,yi). SincedH(w1,w2)=1,(xi,yi)∈C4.(xi,yi)∈C4,(xi,yi)is fault-free,then there exists a pathP0of every odd lengthl0joiningxiandyi,where 1≤l0≤3.LetC=〈x,P1,y,yi,P0,xi,x〉with even length.Since 1≤l0≤3 and 35,6≤l≤10.

Since=1,by Lemma 3,there exists a cycleC1of every even lengthl1containingein,where 4≤l1≤6.Let(x,y)be a fault-free edge in cycleC1such that(xi,yi)(or)is fault-free in.Hence,there exists a pathP1of every odd lengthjoiningxandyin,where 35.dH(w1,w2)=3, through observation,(xi,yi)∈C6(or∈C6).We can choose(xi,yi),then, there exists a pathP0of every odd lengthl0joiningxiandyiin,wherel0=5. LetC=〈x,P1,y,yi,P0,xi,x〉with even length.Sincel0=5 and,10≤l≤12.LetC=〈x,P1,y,yi,xi,x〉with even length, where.Then 6≤l≤8.So 6≤l≤12.

(3)e∈Ei.

Let(x,y)be a fault-free edge in such that(xi,yi)is fault-free in

(x,y)∈C4,(x,y)is a fault-free edge,there exists a pathP0of every odd lengthl0joiningxandyin,where 1≤l0≤3.Since,by Lemma 4,there exists a pathP1of every odd lengthl1joiningxiandyiin,where 3≤l1≤5.LetC=〈x,P0,y,yi,P1,xi,x〉with even lengthl=l0+l1+2.Since 1≤l0≤3 and 3≤l1≤5,6≤l≤10.

Let(x,y)be a fault-free edge in such that(xi,yi)is fault-free in.Through observation,(x,y)∈C6,there exists a pathP0of every odd lengthl0joiningxandyin,wherel0=5.Since,by Lemma 4,there exists a pathP1of every odd lengthl1joiningxiandyiin,where 3≤l1≤5.LetC=〈x,P0,y,yi,P1,xi,x〉with even lengthl=l0+l1+2.Sincel0=5 and 3≤l1≤5,10≤l≤12.LetC=〈x,y,yi,P1,xi,x〉with even lengthl=1+l1+2.Since 3≤l1≤5,6≤l≤8. Therefore,6≤l≤12.

(4)e∈Ec.Lete=,

Letreplace{xi,yi},the following proof is similar to(3)e∈Ei.The proof is completed.

Theorem 1Assume FFvis any subset of V(FQn).Every edge in FQn-FFvlies on a fault-free cycle of every even length from 6 to2n-2|FFv|inclusive even if|FFv|≤n-1and all faulty vertices are not adjacent to the same vertex,where n≥4.

Proof If|FFv|=fv≤n-2,by Lemma 10,the theorem holds.Whenn=4, Lemma 12 holds.Therefore,we only need to consider the situation of|FFv|=fv=n-1,wheren≥5.By Lemma 1,FQncan be partitioned along dimensioniinto twon-1-cubes,denoted byand.There must exist anisuch that,and(v),(We can simply divide one of the faulty vertex and the other faulty vertices into dif f erent parts(or)along ani-dimension.The proof is the condition that all faulty vertices are not adjacent to the same vertex.We can consider extreme situation.Ifn-2 faulty vertices are adjacent to the same vertexx,we can choose one ofn-2 faulty vertices, denoted byy,thenxandyhave one bit dif f erently.So we can partition along this dimension.Thereforeyis in a part,other faulty vertices is in another part and all faulty vertices are not adjacent to the same vertex in this part).

Let,i=0,1,=n-1.eis a fault-free edge.

Case 1.1.

Since=n-2,by Lemma 2,there exists a cycleC0of every even lengthl0containingein,where.Let(x,y)be a fault-free edge in cycleC0such that(xi,yi)(or)is fault-free in(Since=1).LetC0=〈x,P0,y,x〉,then=l(P0),.Since,by Lemma 3,there exists a cycleC1of even lengthl1containing edge(xi,yi)(or)inwhere.Hence,there exists a pathP1of odd lengthjoiningxiandyi(orand),where.LetC=〈x,P0,y,yi,P1,xi,x〉orC=〈x,P01with even length.Sinceand,10≤l≤2n-2().We can obtain the desired even cycle of length from 6 to 8 inC0,where 6≤l0≤2n-1-.So 6≤l≤2n-2().

Case 1.2

Since,by Lemma 3,there exists a cycleC1of even lengthl1containing edgeein,where.LetCkbe a fault-freek-cycle covering the edgeein,where.Obviously,there aremutually disjoint edges excludingeinCk.2()is easy to be hold,where.Thus,there exists an(x,y)which is a fault-free edge in cycleC1such that(xi,yi)(or)is fault-free in.LetC1=〈x,P1,y,x〉, then=l(P1),32n-1--1.Since=n-2,and(xi,yi)(or)is fault-free edge,by Lemma 2,there exists a cycleC0of even lengthl0containing edge (xi,yi)(or)in,where 6≤l0≤2n-1-.Hence,there exists a pathP0of odd lengthjoiningxiandyi(orand),where 52n-1--1.LetC=〈x,P1,y,yi,P0,xi,x〉orC=〈x,P10with even lengthSinceand,10≤l≤2n-2(). We can obtain the desired even cycle of length from 6 to 8 inC1,where 4≤l1≤2n-1-.So 6≤l≤2n-2().

Case 1.3e∈Ei.

Lete=(x,xi).

Since=n-2=1,(u),,xhas at least 2 fault-free neighborsy1,y2in,one of themust be fault-free in. Therefore,there must exist an edge(x,y)insuch that(xi,yi)is fault-free in.Since=n-2,by Lemma 2,there exists a cycleC0of every even lengthl0containing(x,y)in,where 6≤l0≤2n-1-.LetC0=〈x,P0,y,x〉,then=l(P0),52n-1--1.Since=1,by Lemma 6,there exists a cycleP1of odd lengthl1joiningxiandyi,where 3≤l1≤2n-1--1.Since (xi,yi)is fault-free,there exists a cycleof odd lengthjoiningxiandyi,where.LetC=with even lengthSinceand,8≤l≤2n-2. LetC=〈x,y,yi,P1,xi,x〉withl=1+l(P1)+2,l(P1)=3,we can obtain the desired even cycle of length 6.So 6≤l≤2n-2().

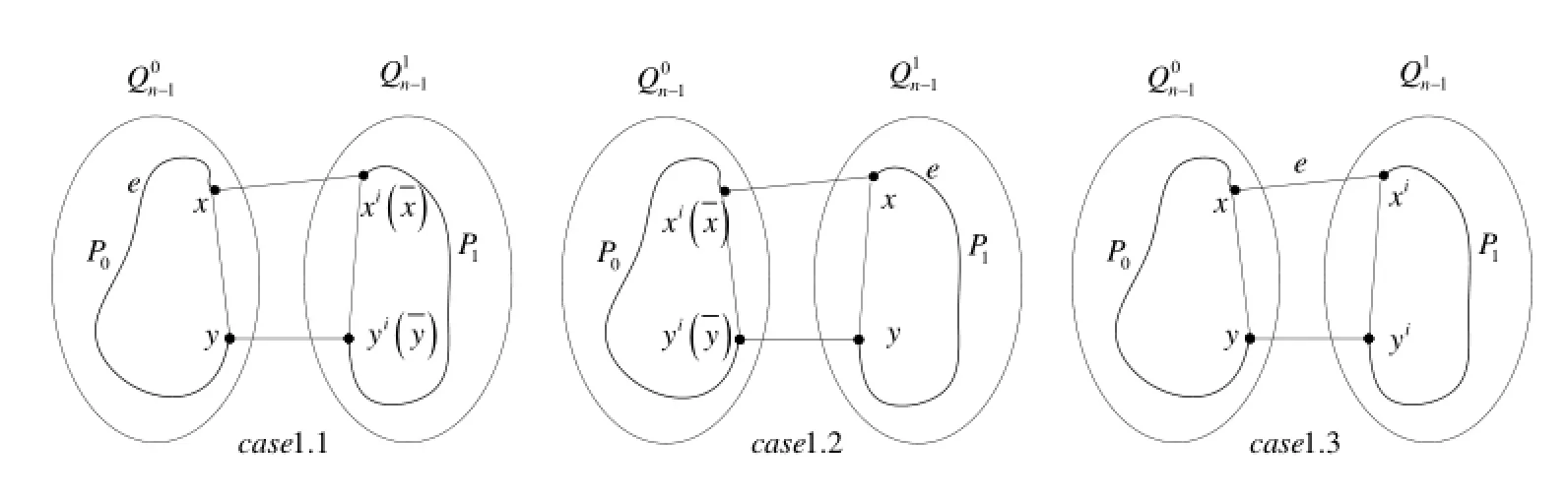
Case 1.4e∈Ec.

The following proof is similar to Case 1.3.

Case 2.1.

Since3,by Lemma 3,there exists a cycleC0of every even lengthl0containing edgeein,where 4≤l0≤2n-1-.LetCkbe a fault-freek-cycle covering the edgeein,wherek=2n-1-.Obviously,there are 2n-2mutually disjoint edges excludingeinCk.2(2n-2)is easy to be hold, where3.Thus,there exists an(x,y)which is a fault-free edge in cycleCksuch that(xi,yi)(or)is fault-free in.Then,there exists a pathP0of every odd lengthjoiningxandyin,where. Since,by Lemma 3,there exists a cycleC1of every even lengthl1containing edge(xi,yi)(or)in,where 4≤l1≤2n-1-.(xi,yi)(oris fault-free edge,so there exists a pathP1of odd lengthjoiningxiandyi(orand),where.LetC=〈x,P0,y,yi,P1,xi,x〉orC=〈x,P01with even length.Since 3and,6≤l≤2n-.

Case 2.2.

The following proof is similar to Case 2.1.

Case 2.3e∈Ei.

By Lemma 11,the proof is completed.

Case 2.4e∈Ec.

By Lemma 11,the proof is completed.

The proof of Theorem 1 is f i nished.

4 Conclusion

The folded hypercubeFQnis an important network topology for parallel processing computer systems.According to[4],we can prove the same conclusion inFQn. Under the condition|FFv|≤n-1 and all faulty vertices are not adjacent to the same vertex,we show that ifn≥4,then every edge ofFQn-FFvlies on a fault-free cycle of every even length from 6 to 2n-2|FFv|.

[1]J.M.Xu,Graph and Application of Graphs,Dordrecht/Boston/London:Kluwer Academic publishers,2003.

[2]Y.Saad and M.H.Schultz,Topological properties of hypercubes,IEEE.Trans.on Comput.,37:7(1988),867-872.

[3]C.-H.Tsai,Cycles embedding in hypercubes with node failures,Information Processing Letters,102(2007),242-246.

[4]C.-H.Tsai,C.-R.Yu,Embedding various even cycles in a hypercube with node failures,The 24th Workshop on Combinatorial Mathematics and Computation Theory,2007, 237-243.

[5]S.-Y.Hsieh,T.-H.Shen,Edge-bipancyclicity of a hypercube with faulty vertices and edges,Discrete Applied Mathematics,156(2008),1802-1808.

[6]S.-Y.Hsieh,C.-N.Kuo,H.-L.Huang,1-vertex-fault-tolerant cycles embedding on folded hypercubes,Discrete Applied Mathematics,15(2009),3094-3098.

[7]M.J.Ma,J.M.Xu,Z.Z.Du,Edge-fault-tolerant hamiltonicity of folded hypercube,Journal of University of Science and Technology of China,36:3(2006),244-248.

[8]C.N.Kuo,S.Y.Hsieh,Pancyclicity and bipancyclicity of conditional faulty folded hypercubes,Information Sciences,180(2010),2904-2914.

[9]J.M.Xu,M.J.Ma,Z.Z.Du,Edge-fault-tolerant properties of hypercubes and folded hypercubes,Australasian Journal of Combinatorics,35(2006),7-16.

[10]D.Q.Cheng,R.X.Hao,Y.Q.Feng,Cycles embedding on folded hypercubes with faulty nodes,Discrete Applied Mathematics,161(2013),2894-2900.

[11]S.-Y.Hsieh,C.-N.Kuo,Hamiltonian-connectivity and strongly Hamiltonian-laceability of folded hypercubes,Computers and Mathematics with Applications,53(2007),1040-1044.

[12]M.Ma,G.Liu,X.Pan,Path embedding in faulty hypercubes,Applied Mathematics and Computation,192(2007),233-238.

[13]D.Q.Cheng,R.X.Hao,Y.Q.Feng,Embedding even cycles on folded hypercubes with conditional faulty edges,Information Processing Letters,115(2015),945-949.

[14]Weiping Han,S.Y.Wang,The g-Extra Conditional Diagnosability of Folded Hypercubes,Applied Mathematical Sciences,146:9(2015),7247-7254.

[15]D.Q.Cheng,R.X.Hao,Y.Q.Feng,Odd cycles embedding on folded hypercubes with conditional faulty edges,Information Sciences,282(2014),180-189.

(edited by Liangwei Huang)

∗This project was supported by NSFC(11371162)and NSFC(11171129)and HuBei (T201103).

†Manuscript received

‡Corresponding author.E-mail:1101358757@qq.com