EXISTENCE OF PERIODIC SOLUTIONS OF A CLASS OF SECOND-ORDER NON-AUTONOMOUS SYSTEMS∗†

Yuan Qi,Kun Liu

(College of Math.and Statistics,Longdong University,Gansu 745000,PR China)

EXISTENCE OF PERIODIC SOLUTIONS OF A CLASS OF SECOND-ORDER NON-AUTONOMOUS SYSTEMS∗†

Yuan Qi‡,Kun Liu

(College of Math.and Statistics,Longdong University,Gansu 745000,PR China)

In this paper,we are concerned with the existence of periodic solutions of second-order non-autonomous systems.By applying the Schauder’s f i xed point theorem and Miranda’s theorem,a new existence result of periodic solutions is established.

second-order non-autonomous systems;periodic solutions; Schauder’s f i xed point theorem;Miranda’s theorem

2000 Mathematics Subject Classification 34B15;34C25;37J45

1 Introduction

In the past few years,there has been considerable interest in the existence of periodic solutions of the following second-order periodic boundary value problems

wherea,c∈L1(0,T)andf:[0,T]×R→R is continuous.For more details please see[1-6]and the references therein.In particular,many authors mentioned above paid their attention to the non-resonant case,that is,the unique solution of the following linear problem

is the trivial one.To the end,the functionais supposed to satisfy the basic assumption:

(H0)The Green’s functionG(t,s)of the linear problem(1.1)is nonnegative for every(t,s)∈[0,T]×[0,T].See[3]for the details.

It is well known that if(1.1)is non-resonant andhis aL1-function then the Fredholm’s alternative theorem implies that the nonhomogeneous problem

always has a unique solution,which can be written as

And consequently,the linear problem(1.1)is non-resonant.On the other hand, several authors have focused their attention to the existence of periodic solutions of the second-order nonlinear systems.Here we refer the readers to Chu,Torres and Zhang[7],Franco and Webb[8],Cao and Jiang[9]and Wang[10].Especially in[9],Cao and Jiang obtained several existence results of periodic solutions of the following second order coupled systems

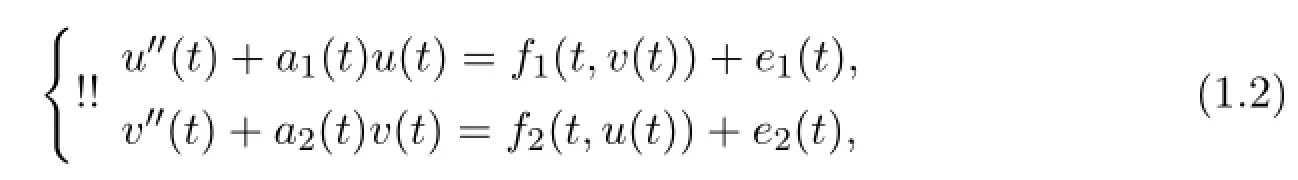
wheref,g:(R/TZ)×R×R→R are continuous andai,ei∈C(R/TZ,R),i=1,2.

Clearly,the above mentioned papers all dealt with the non-resonant problems, that isai(t)0,i=1,2.Now,the natural question is whether or not there is a periodic solution of(1.2)ifai(t)≡0,i=1,2?

In this paper,we shall establish a new existence result of periodic solutions of the resonant coupled systems

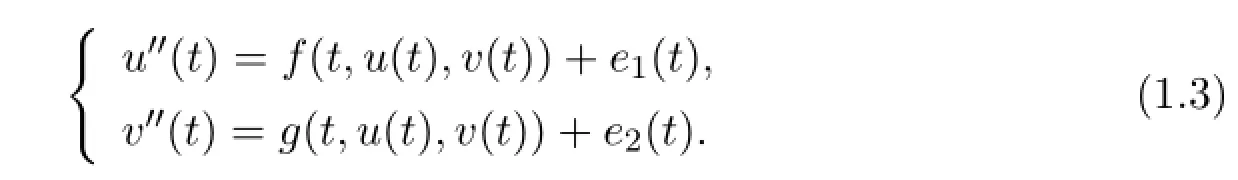
To the best of our knowledge,the existence results of periodic solutions of the above systems are relatively little,and our result shall f i ll this gap.

The main result of this paper is as follows.

Theorem 1.1Suppose that

(H1)f,g∈C((R/TZ)×R×R,R)are bounded.There are two positive constants l1and l2such that for each(t,x,y)∈R×R×R,

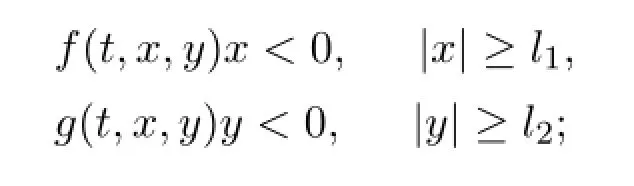
(H2)ei∈C(R/TZ,R)with mean value

Then(1.3)has a periodic solution.

The Miranda’s theorem below will be crucial in our arguments.

Theorem A[11]Let

Suppose that the mapping F=(F1,F2,···,Fn):Rnis continuous on theclosureof G,such that F(x)=(0,0,···,0)for x on the boundary∂G of G.In addition,

(i)Fi(x1,x2,···,xi-1,-L,xi+1,···,xn)≥0 for 1≤i≤n and

(ii)Fi(x1,x2,···,xi-1,+L,xi+1,···,xn)≤0 for 1≤i≤n. Then,F(x)=θ has a solution in G.

2 Proof of Theorem 1.1

Def i ne an operatorL:D(L)→Eby

whereEis a Banach space composed of continuousT-periodic functions with the norm

and

Then it is not difficult to check thatLis not invertible since Ker(L)={c},c∈R.

LetV=Ker(L).ThenL2(0,T)=V⊕V⊥,where

Now,u,v∈L2(0,T)can be rewritten as

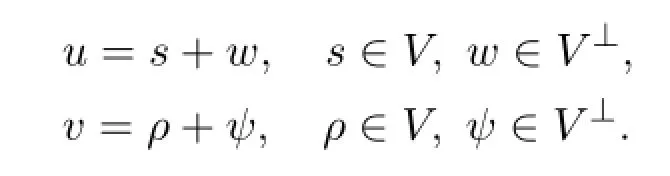
And from(H2)it follows that(1.3)is equivalent to the following equations

By(2.1)and(2.3),we get

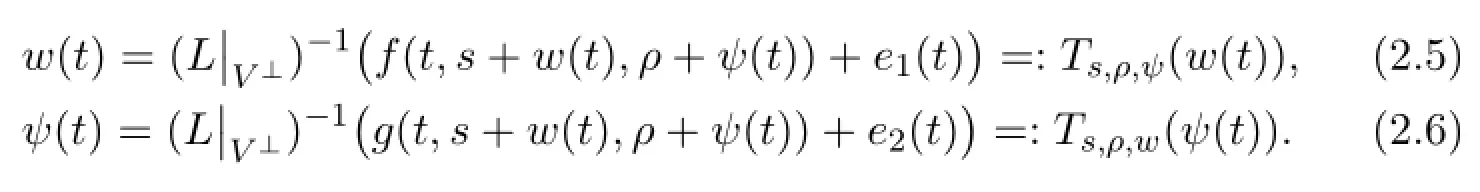
Moreover,(H1)implies there existM1＞0,M2＞0 such that

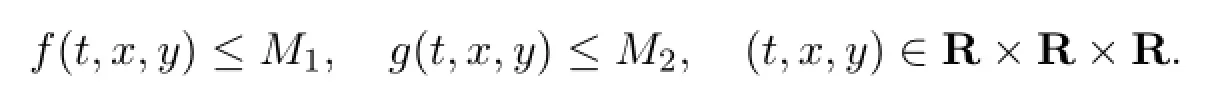
Thus,by Schauder’s f i xed point theorem,equations(2.5)and(2.6)have solutionsand,respectively.Furthermore,each possible solutionwof(2.5)is bounded,so there is a constantL1＞0 such that‖w‖≤L1.Similarly,each possible solutionψof(2.6)satisf i es‖ψ‖≤L2for some constantL2＞0.

and

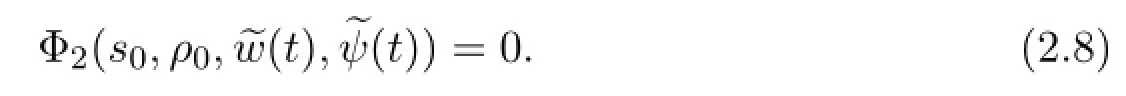
Clearly,it follows from(H1)that there exists a constants1＞0 sufficiently large such that

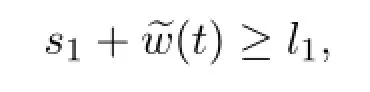
therefore

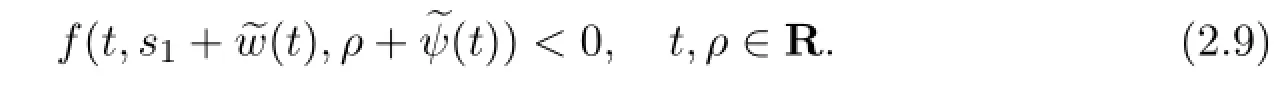
On the other hand,there exists a constants2＜0 with|s2|large enough such that

therefore

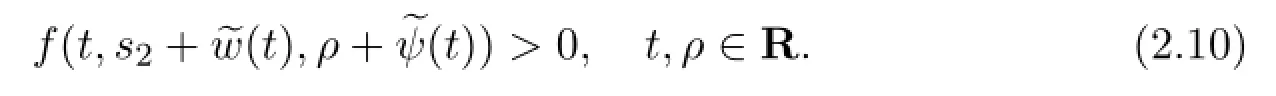
Similarly,we may chooseρ1＞0 andρ2＜0 withρ1and|ρ2|sufficiently large such that

and accordingly,

Let

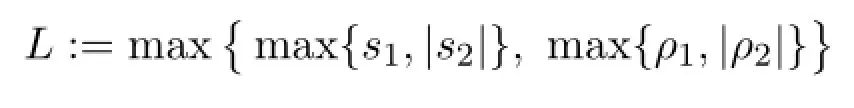
and

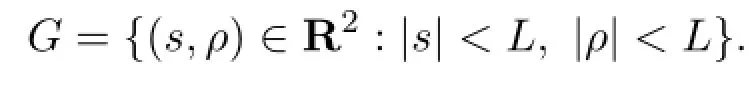
Def i ne

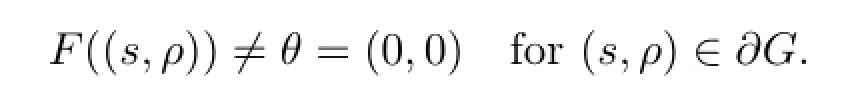
Finally,let us show that assumptions(i)and(ii)of Theorem A are also satisfied. To prove Theorem A(i),it is equivalent to prove

Since

the f i rst inequality in(H1)implies(2.13)holds.On the other hand,the second inequality in(H1)and the fact

yield(2.14)is also satisfied.

To prove Theorem A(ii),it is equivalent to prove

By the similar arguments as in the proof of(2.13)and(2.14),we can show that (2.15)and(2.16)are also satisfied.

Consequently,Theorem A implies there exists an(s0,ρ0)∈Gsuch that

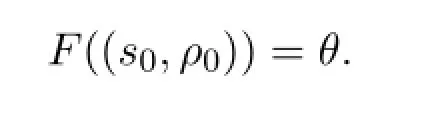
Therefore,(2.7)and(2.8)hold,and the proof is completed.

[1]I.Rachunkov´a,M.Tvrd´y,I.Vrkoˇc,Existence of nonnegative and nonpositive solutions for second order periodic boundary value problems,J.Dif f.Equs.,176(2001),445-469.

[2]P.J.Torres,Existence of one-signed periodic solutions of some second-order dif f erential equations via a Krasnoselskii f i xed point theorem,J.Dif f.Equs.,190(2003),643-662.

[3] P.J.Torres,Weak singularities may help periodic solutions to exist,J.Dif f.Equs., 232(2007),277-284.

[4]J.Chu,M.Li,Positive periodic solutions of Hill’s equations with singular nonlinear perturbations,Nonlinear Anal.,69(2008),276-286.

[5] X.Li,Z.Zhang,Periodic solutions for second-order dif f erential equations with a singular nonlinearity,Nonlinear Anal.,69(2008),3866-3876.

[6]H.Li,Positive periodic solutions of second-order dif f erential equations with singularities,Bull.Austral.Math.Soc.,78(2008),163-169.

[7]J.Chu,P.J.Torres,M.Zhang,Periodic solutions of second order non-autonomous singular dynamical systems,J.Dif f.Equs.,239(2007),196-212.

[8] D.Franco,J.R.L.Webb,Collisionless orbits of singular and nonsingular dynamical systems,Discrete Contin.Dyn.Syst.,15(2006),747-757.

[9]Z.Cao,D.Jiang,Periodic solutions of second order singular coupled systems,Nonlinear Anal.,71(2009),3661-3667.

[10] H.Wang,Positive periodic solutions of singular systems with a parameter,J.Dif f. Equs.,249(2010),2986-3002.

[11] C.Miranda,Un’osservatione su un teorema di Brouwer,Boll.Un.Mat.Ital., 3:2(1940),5-7.

(edited by Liangwei Huang)

∗Supported by the Fundamental Research Funds for the Gansu Universities(2015A-150),the PhD scientif i c research start-up capital funded projects of Longdong University (XYBY05).

†Manuscript received

‡Corresponding author.E-mail:mathqy@163.com