A NEW CLASS OF SOLUTIONS OF VACUUM EINSTEIN’S FIELD EQUATIONS WITH COSMOLOGICAL CONSTANT∗†
2016-04-18MingShenQiaorongZhuang
Ming Shen,Qiaorong Zhuang
(College of Math.and Computer Science,Fuzhou University,Fuzhou 350116,
E-mail:shenming0516@fzu.edu.cn(M.Shen))
A NEW CLASS OF SOLUTIONS OF VACUUM EINSTEIN’S FIELD EQUATIONS WITH COSMOLOGICAL CONSTANT∗†
Ming Shen,Qiaorong Zhuang
(College of Math.and Computer Science,Fuzhou University,Fuzhou 350116,
E-mail:shenming0516@fzu.edu.cn(M.Shen))
In this paper,a new class of solutions of the vacuum Einstein’s field equations with cosmological constant is obtained.This class of solutions possesses the naked physical singularity.The norm of the Rieman n curvature tensor of this class of solutions takes inf i nity at some points and the solutions do not have any event horizon around the singularity.
vacuum Einstein’s field equations;cosmological constant;exact solutions;naked physical singularity
2000 Mathematics Subject Classification 83C05;83C75;35C05
1 Introduction
The cosmological constant problem is one of the most outstanding and unsolved problems in cosmology.It has been a focal point of interest[1-4].From our point of view,the universe possesses a non-zero cosmological constant which is considered as the vacuum energy density.The cosmological term provides a repulsive force opposing the gravitational pull between the galaxies.The recent measurements of type Ia Supernovae observations[5,6] and findings from the anisotropy measurements of the cosmic microwave background by the Wilkinson Microwave Anisotropy Probe[7]have shown that our universe is undergoing an accelerated expansion.It is the most accepted idea that a mysterious dominant component dubbed dark energy leads to this cosmic acceleration.The cosmological constant is a strong candidate for dark energy which pushes the universe accelerated expansion.
Exact solutions of Einstein’s field equations with cosmological constant,which of f er an alternative and complementary approach to study cosmological models,have been investigated from time to time.As early as 1918,Kottler extended the Schwarzschild solution and obtained the static spherically symmetric exterior solution with cosmological constant.Kramer et al.got the Reissner-Nordsr¨om exterior solution with cosmological constant[8].Xu,Wu and Huang extended the Florides’solution to the case with cosmological constant[9].Recently,Nurowski provided the f i rst examples of vacuum metricswith cosmological constant which have a twisting quadruple principal null direction[10]. Kamenshchik and Mingarelli found an exact solution of a Bianchi-I Universe in the presence of dust,stif fmatter and a negative cosmological constant,generalising the well-known Heckmann-Schucking solution[11].Landry,Abdelqader and Lake studied the McVittie solution with a negative cosmological constant and they found that cosmological constant Λ<0 ensures collapse to a Big Crunch[12].Zubairi and Weber[13]derived the modified Tolman-Oppenheimer-Volkof fequations which account for a f i nite value of the cosmological constant for spherically symmetric mass distributions.
In this paper,we consider the vacuum Einstein’s field equations with cosmological constant of the following form
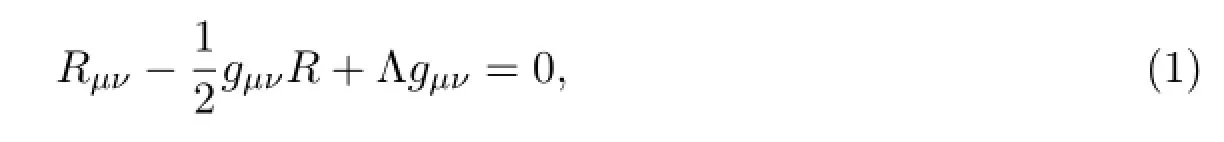
or equivalently
They are solved by presenting a special form of Lorentzian metric and taking a proper ansatz.It is shown that this new class of solutions possesses naked physical singularity. Moreover,the solutions presented in this paper extend the results of[14]to the case with cosmological constant.
2 The Solutions with Cosmological Constant
In the coordinate(t,x,y,z),consider the metric of the form
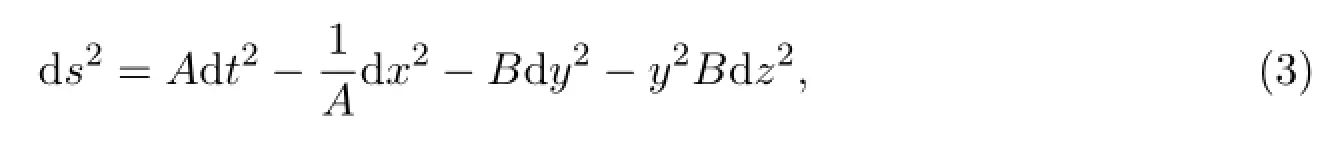
whereA=A(t,x)andB=B(t,x).It is easy to verify that the determinant of metric (gµν)is given by
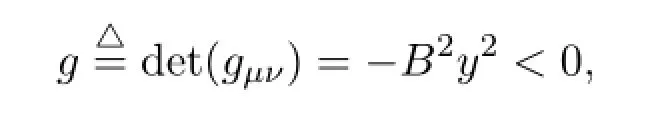
so the metric(gµν)is Lorentzian.
In view of metric(3),the vacuum Einstein’s field equations with cosmological constant (2)reduce to the following system
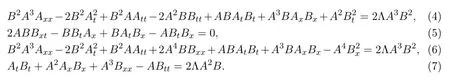
In order to simplify system(4)-(7),we take the ansatz as follows

and

De fi ner=x-tand denote,then equation(5)reduces to

which gives
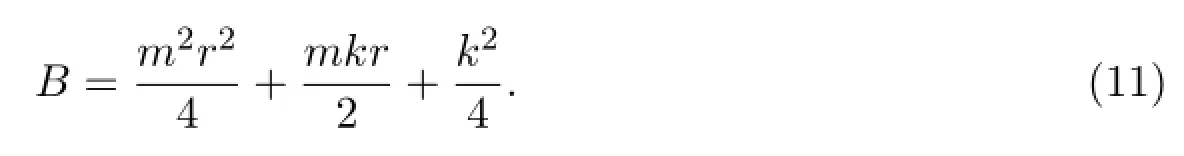
Heremandkare two constants of integration.Letting

and

we have

Substituting(14)into equations(4),(6)and(7)yeilds
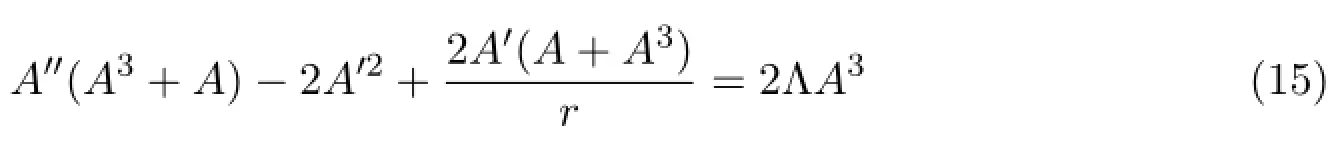
and
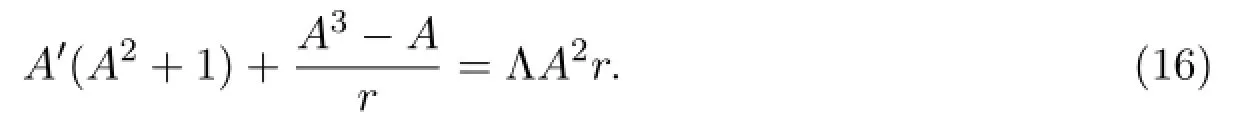
Solving equation(15)gives
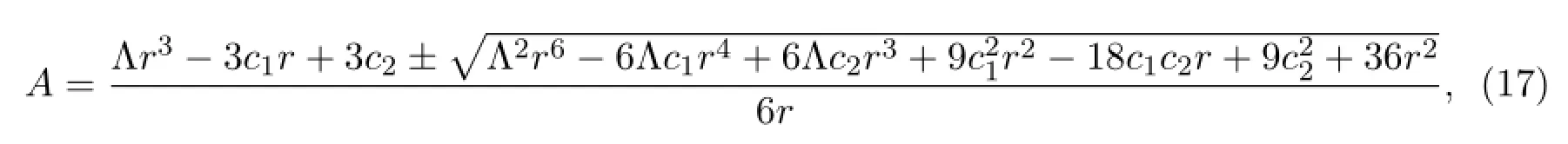
wherec1andc2are integration constants.Takingc1=0 yields
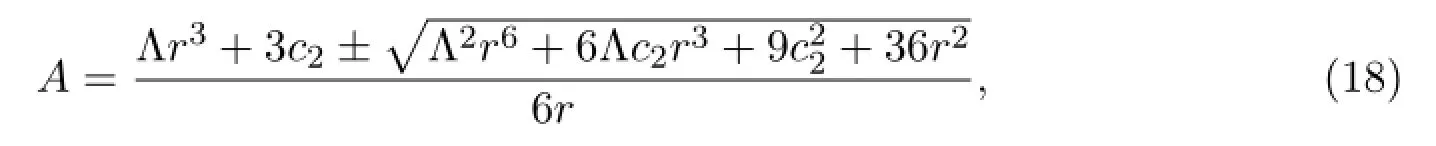
which are exactly the solutions of equation(16).In view ofr=x-t,we f i nally have
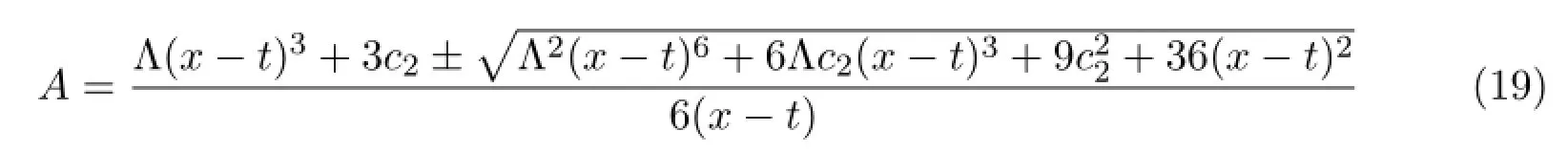
and

From the above discussion,we obtain the following theorem.
Theorem 2.1In the coordinates(t,x,y,z),the vacuum Einstein’s f i led equations with cosmological constantΛhave the following solutions
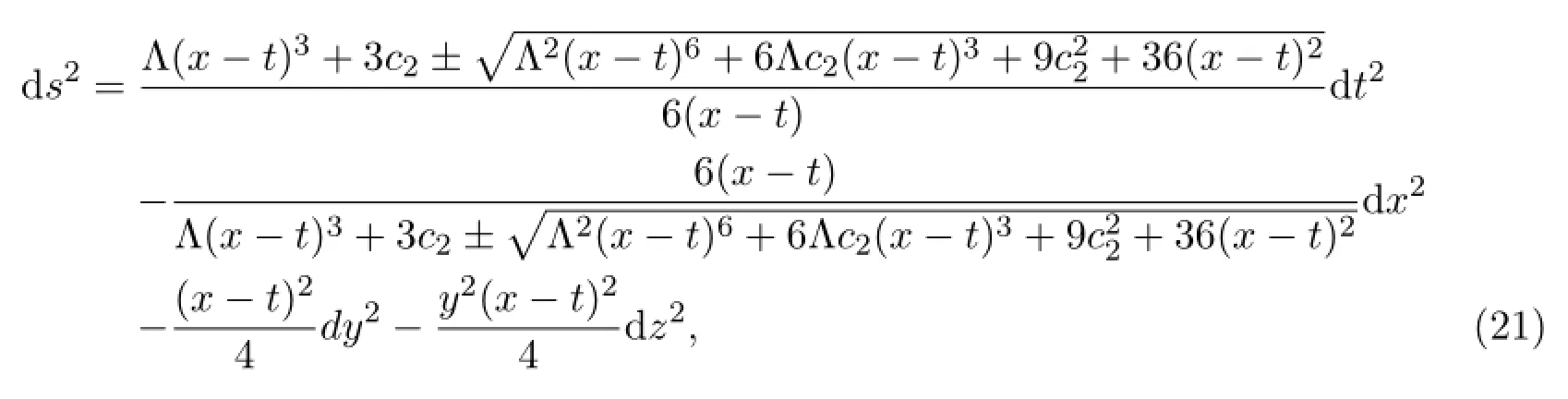
where c2is an integration constant.
As is shown by the def i nition

we get the following theorem.
Theorem 2.2In the coordinates(t,r,y,z),the solutions of vacuum Einstein’s f i led equations with cosmological constant Rµν=Λgµν(µ,ν=0,1,2,3)become
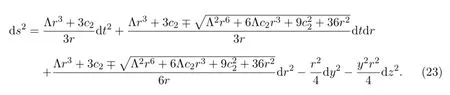
3 Singularity
This section is devoted to the analysis of singularity of(23)of the vacuum Einstein’s fi eld equations with cosmological constant.By calculations,the corresponding Riemann curvature tensor of(23)reads as

and the otherRαβµν=0.
Obviously,the non-vanishing Riemann curvature tensor tends to inf i nity whenr→0. By further calculations and analysis,we obtain the norm of the Riemann curvature tensor
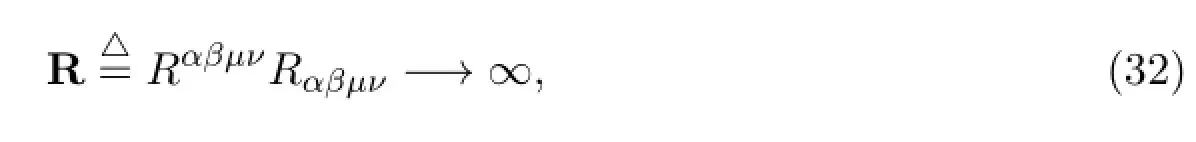
whiler→0.Thus,r=0 is a physical singularity of the space-time described by(23). From(23)-(31),it is easy to get that no event horizon exists around the physical singularityr=0.It can be concluded that(23)possess a naked physical singularityr=0.
4 Summary and Discussions
When Λ=0,(21)reduce to
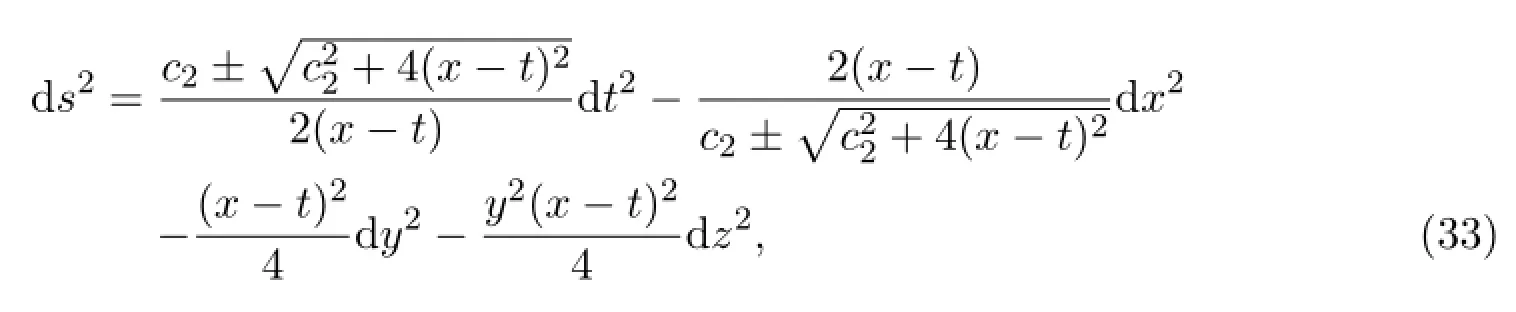
which are the solutions of the vacuum Einstein’s field equations with vanishing cosmological constant
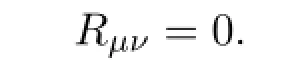
In particular,taking

and
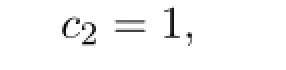
we have
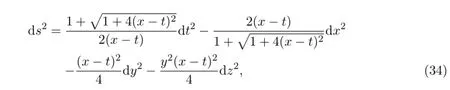
which is exactly the solution presented in[14].Thus the solutions in Theorem 2.1 include the results obtained in[14]and extend the solutions to the case with cosmological constant.
Moreover,the solutions with cosmological constant obtained here possess naked physical singularity,that is,no event horizon exists around the physical singularity.It is expected that this new class of solutions can be applied to modern cosmology.
[1]T.Sauer,On Einstein’s early interpretation of the cosmological constant,Annalen der Physik, 524(2012),A135-A138.
[2]A.Alonso-Serrano,C.Bastos,O.Bertolami and S.Robles-P´erez,Interacting universes and the cosmological constant,Physics Letters B,719(2013),200-205.
[3]D.Brizuela,Classical versus quantum evolution for a universe with a positive cosmological constant,Physical Review D,8(2015),085003.
[4]K.Karimiyan,J.Naji,Interacting viscous modified chaplygin gas cosmology in presence of cosmological constant,International Journal of Theoretical Physics,53(2014),2396-2403.
[5]A.G.Riess,et al.,Observational dvidence from supernovae for an accelerating universe and a cosmological constant,Astron.J.,116(1998),1009-1038.
[6]A.G.Riess et al.,Type Ia supernova discoveries atz>1 from the Hubble space telescope: evidence for past deceleration and constraints on dark energy evolution,Astrophysical Journal, 607(2004),665-687.
[7]C.L.Bennett,et al.,First year wilkinson microwave anisotropy probe(WMAP)observations: Implications for inf l ation,The Astrophysical Journal Supplement,148(2003),213-231.
[8]D.Kramer,H.Stephani,M.MacCallum and E.Herlt,Exact solutions of Einstein’s field equations,Cambridge Monographs on Mathematical Physics,Cambridge University Press, Cambridge,1980.
[9]C.M.Xu,X.J.Wu and Z.Huang,A new class of spherically symmetric interior solution with cosmological constant Λ,General Relativity and Gravitation,19(1987),1203-1211.
[10]P.Nurowski,Twisting typeNvacuums with cosmological constant,Journal of Geometry and Physics,58(2008),615-618.
[11]A.Y.Kamenshchik and C.M.F.Mingarelli,A generalized Heckmann-Schucking cosmological solution in the presence of a negative cosmological constant,Physics Letters,693(2010),213-217.
[12]P.Landry,M.Abdelqader and K.Lake,The McVittie solution with a negative cosmological constant,Physical Review D,86(2012),084002.
[13]O.Zubairi and F.Weber,Solutions of Einstein’s field equation modified for the cosmological constant,Astronomische Nachrichten(Astronomical Notes),335(2014),593-598.
[14]M.Shen, A new solution to Einsteins field equations,ChinesePhysicsLetters, 26(2009),060401.
(edited by Liangwei Huang)
∗The work was supported by National Natural Science Foundation of China(Grant No.11101085) and Natural Science Foundation of Fujian Province(Grant No.2015J0101).
†Manuscript received July 8,2015;Revised November 3,2015
杂志排行
Annals of Applied Mathematics的其它文章
- GLOBAL FINITE ENERGY WEAK SOLUTION TO THE VISCOUS QUANTUM NAVIERSTOKES-LANDAU-LIFSHITZ-MAXWELL MODEL IN 2-DIMENSION∗
- INFORMATION FOR AUTHORS
- EXACT SOLUTIONS OF(2+1)-DIMENSIONAL NONLINEAR SCHR¨ODINGER EQUATION BASED ON MODIFIED EXTENDED TANH METHOD∗
- EVANS FUNCTIONS AND INSTABILITY OF A STANDING PULSE SOLUTION OF A NONLINEAR SYSTEM OF REACTION DIFFUSION EQUATIONS∗†
- CYCLES EMBEDDING ON FOLDED HYPERCUBES WITH FAULTY NODES∗†
- EXISTENCE OF PERIODIC SOLUTIONS OF A CLASS OF SECOND-ORDER NON-AUTONOMOUS SYSTEMS∗†
