EXACT SOLUTIONS OF(2+1)-DIMENSIONAL NONLINEAR SCHR¨ODINGER EQUATION BASED ON MODIFIED EXTENDED TANH METHOD∗

Shuhua Zheng,Heng Wang

(College of Statistics and Math.,Yunnan University of Finance and Economics,Yunnan 650021,PR China)

EXACT SOLUTIONS OF(2+1)-DIMENSIONAL NONLINEAR SCHR¨ODINGER EQUATION BASED ON MODIFIED EXTENDED TANH METHOD∗

Shuhua Zheng,Heng Wang†

(College of Statistics and Math.,Yunnan University of Finance and Economics,Yunnan 650021,PR China)

In this paper,the modified extended tanh method is used to construct more general exact solutions of a(2+1)-dimensional nonlinear Schr¨odinger equation. With the aid of Maple and Matlab software,we obtain exact explicit kink wave solutions,peakon wave solutions,periodic wave solutions and their 3D images.

nonlinear Schr¨odinger equation;modified extended tanh method; kink wave solution;peakon wave solution;periodic wave solution

2000 Mathematics Subject Classification

1 Introduction

It is well known that Schr¨odinger equation is one of the most basic equation of quantum mechanics.It ref l ects the state of micro particle changing with time.As it is a powerful tool for solving non relativistic problems in atomic physics,it has been widely used in the field of atomic,molecular,solid state physics,nuclear physics, chemistry and so on.Recently,Searching and constructing exact solutions of nonlinear partial dif f erential(NLPD)equation is very meaningful for it can describe the problems of mechanics,control process,ecological and economic system,chemical recycling system and epidemiological.

In the past several decades,much ef f orts have been made on this aspect and many useful methods have been proposed such as inverse scattering method,Jacobi elliptic function method,F-expansion method,Darboux transform,the sine-cosine method and the tanh method and so on[1-18].Among them,the tanh method is widely used as it can find exact as well as approximate solutions in a systematic way.Subsequently,Fan has proposed an extended tanh method and obtained the travelling wave solutions that can not be obtained by the tanh method.Based onthis approach,we employ the modified extended tanh method to construct a series of exact travelling wave solutions of a(2+1)-dimensional nonlinear Schr¨odinger(NLS) equation as

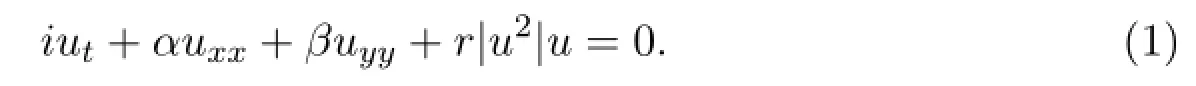
The rest of this paper is organized as follows.In Section 2,we shall introduce the modified extended tanh method.In Section 3,we illustrate this method in detail with the(2+1)-dimensional nonlinear Schr¨odinger(NLS)equation.In Section 4, the image simulations of exact Travelling Wave Solutions of(1)are given.Finally, a short conclusion is given in Section 4.

2 The Modified Extended Tanh Method

In this section,we review the modified extended tanh method.

The modified extended tanh method is developed by Malf l ied in[10,11],and used in[12-14]among many others.Since all derivatives of a tanh can represented by tanh itself,we consider the general NLPDE in two variables

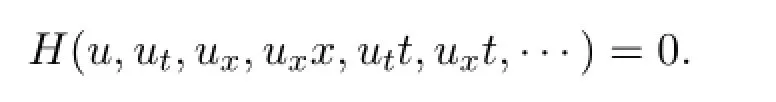
Now we consider its travellingu(x,t)=u(ξ),whereξ=x-ctorξ=x+ctand the equation becomes an ordinary dif f erential equation.We apply the following series expansion

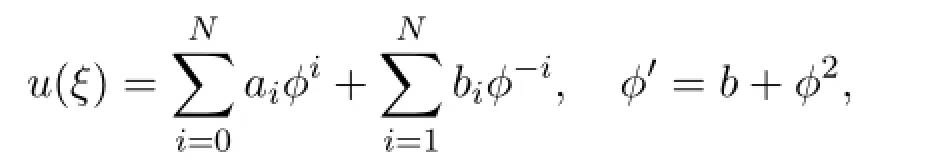
wherebis a parameter to be determined,φ=φ(ξ)and

To determine the parameterN,we usually balance the linear terms of highestorder in the resulting equation with the highest-order nonlinear terms.Then we can get all coefficients of dif f erent powers ofφand determineai,bi,b,cby making them equal to zeros.

The Riccati equation has the following general solutions:

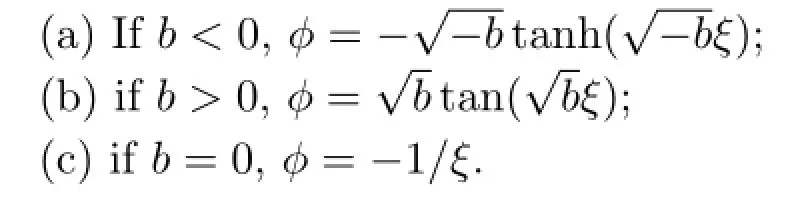
3 Exact Travelling Wave Solutions of(1)

We consider the travelling wave solutionu(x,y,t)=u(ξ),ξ=x+ky-ctof(1), and also

According to(1)and(2),we can get

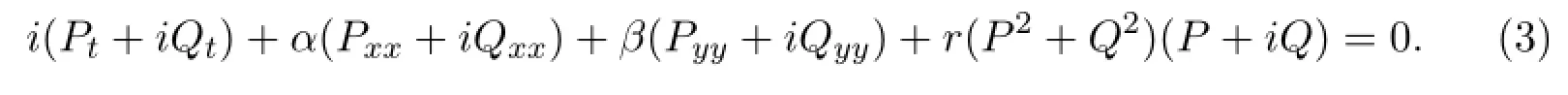
From(3)we can obtain the following two equation

Foru(x,y,t)=u(ξ)andξ=x+ky-ct,we can transform(4)into ordinary dif f erential equations

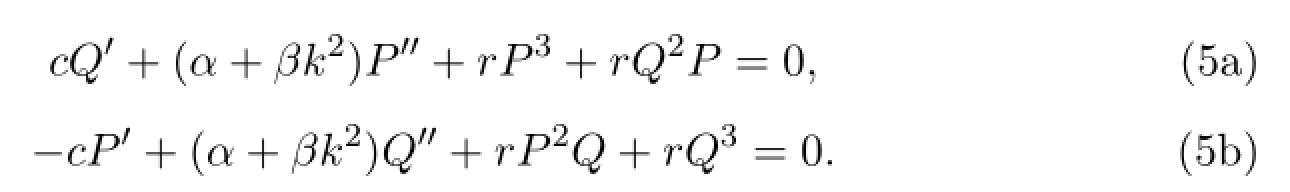
The solution can be expressed as the following form

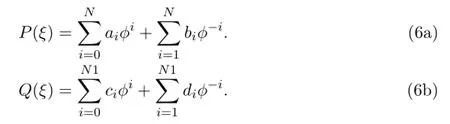
Balancing the linear term of highest order with the nonlinear term in both equations, we find

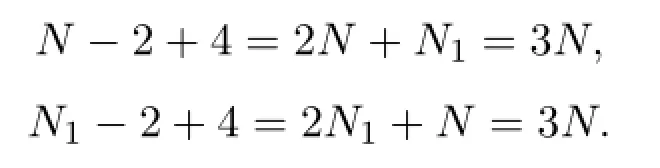
Thus,N=N1=1,and

Withφ＇=b+φ2,we get

Substitute(7)and(8)into the ordinary dif f erential equations(5a)and(5b),then we obtain the coefficients ofφ0,φ,φ2,φ3,φ-1,φ-2andφ-3,respectively,

With the aid of Maple,we obtaina0,a1,b1,c0,c1,d1,b,c,kas follows.

wherer,β,α,k,c0,c1are arbitrary constants.

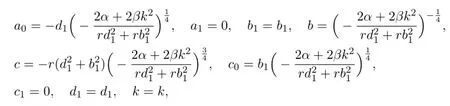
wherer,β,α,k,b1,d1are arbitrary constants.

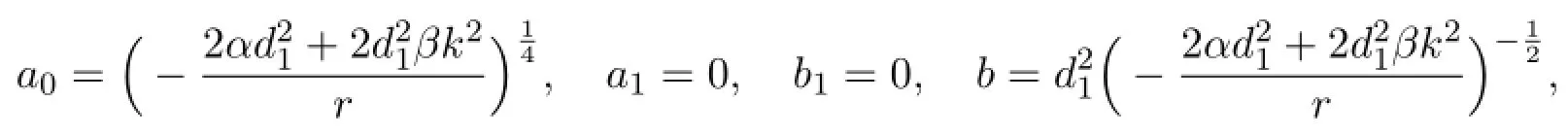
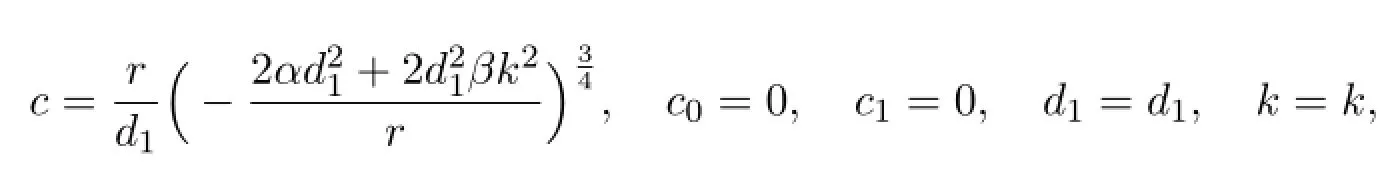
wherer,β,α,k,d1are arbitrary constants.

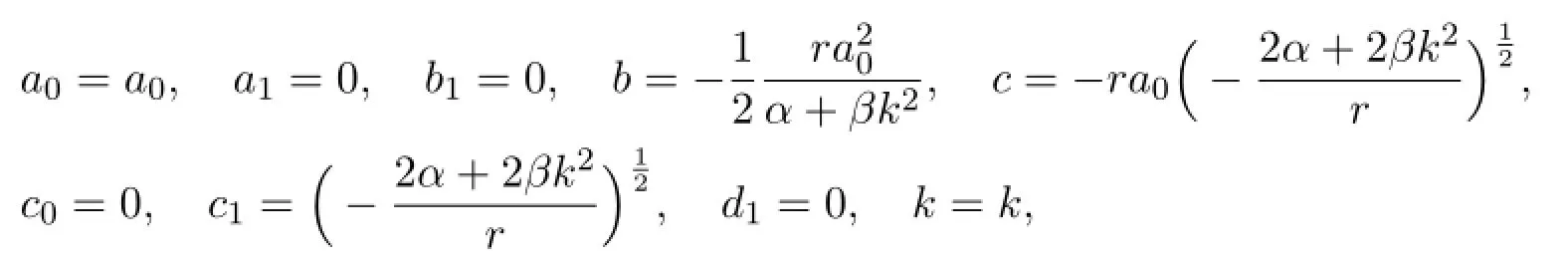
wherer,β,α,k,a0are arbitrary constants.

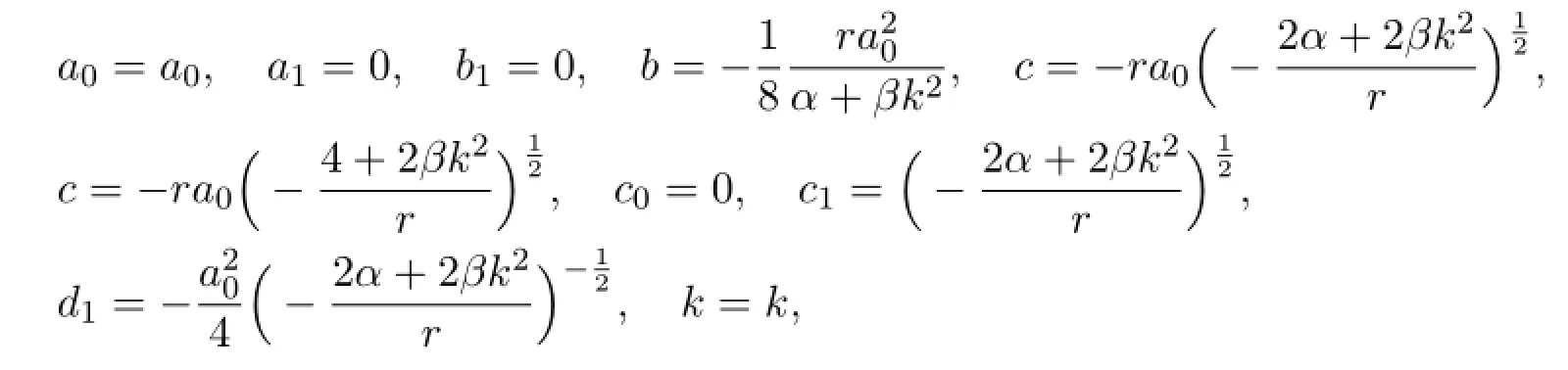
wherer,β,α,k,a0are arbitrary constants.

wherer,β,α,k,c0are arbitrary constants.

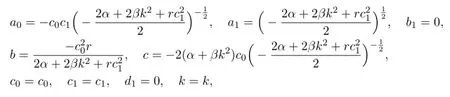
wherer,β,α,k,c0,c1are arbitrary constants.

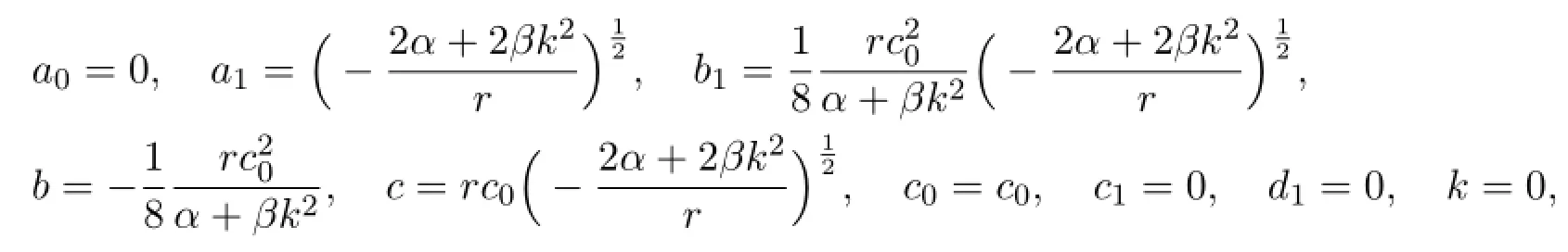
wherer,β,α,k,c0are arbitrary constants.

wherer,β,α,k,c0are arbitrary constants.

Ifb＞0,we get

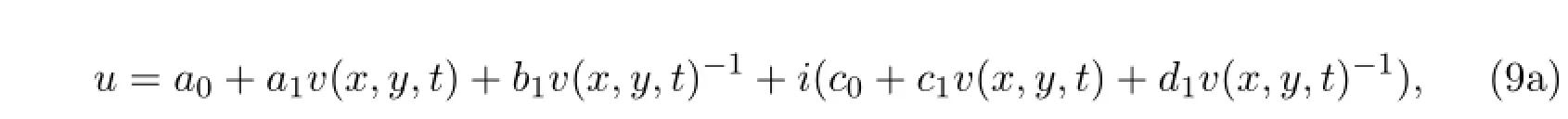
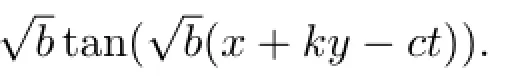
Ifb=0,we get

Ifb＜0,we get

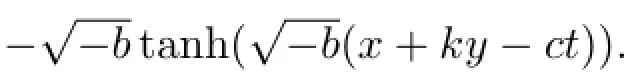
Substituting all those situation into(9)respectively,we can get all solutions of the derivative nonlinear Schr¨odinger equation.

4 Image Simulation

In order to grasp these exact travelling solutions,we choose several exact solutions and use the Matlab software to simulate images.In the process of image simulation,the f i gures and values of parameters we selected are shown as follows.

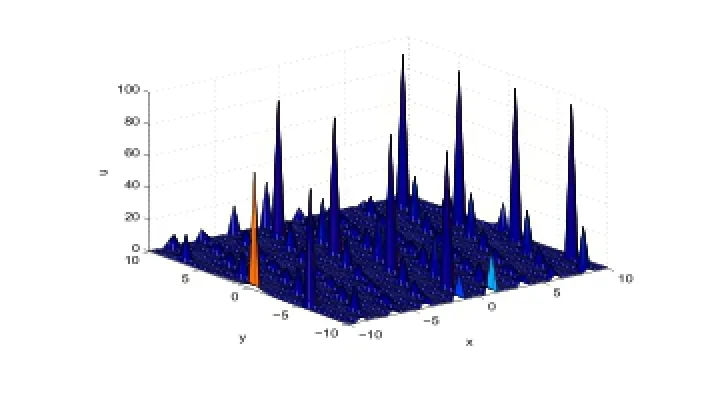
Figure 1:3-dimensional wave of Case (1).

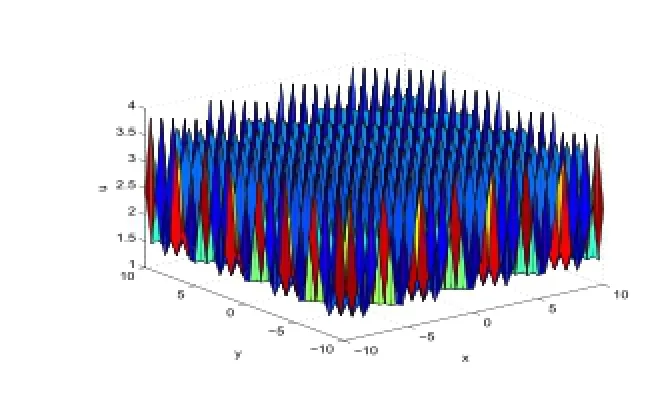
Figure 2:3-dimensional wave of Case (2).

In Figure 1,we taker=-1,β=11,k=0.1,c0=-0.25,c1=0.1,α=-0.2,t=0.1.In Figure 2,we taker=-6,β=-3,k=1,d1=1,α=1,b1=-1,t=0.1.

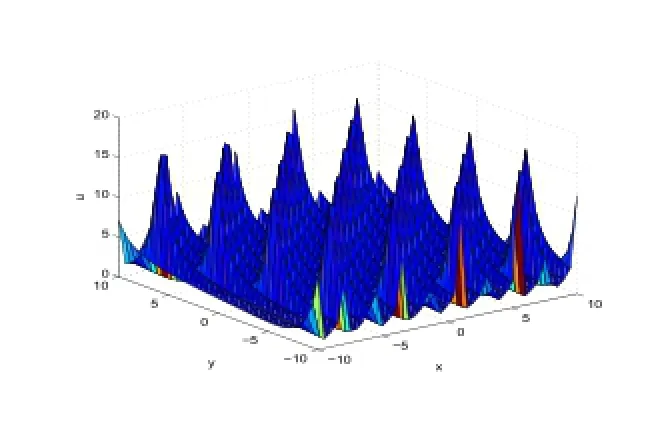
Figure 3:3-dimensional wave of Case (3).

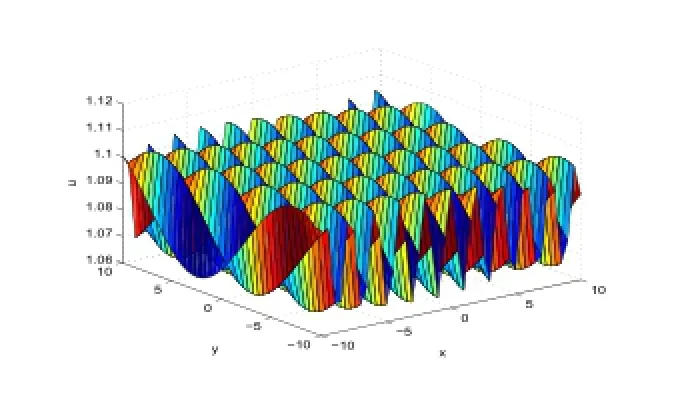
Figure 4:3-dimensional wave of Case (3).

In Figure 3,we taker=0.1,β=0.3,k=0.1,d1=-2,α=0.2,t=0.1.In Figure 4,we taker=-6,β=2,k=0.1,c0=6,α=-4,d1=2,t=0.1.

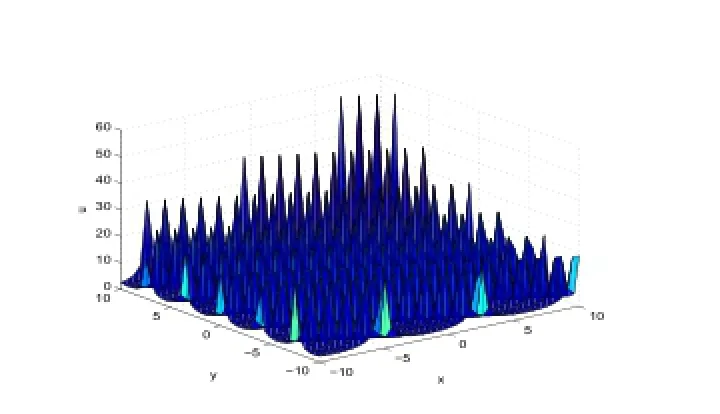
Figure 5:3-dimensional wave of Case (4).

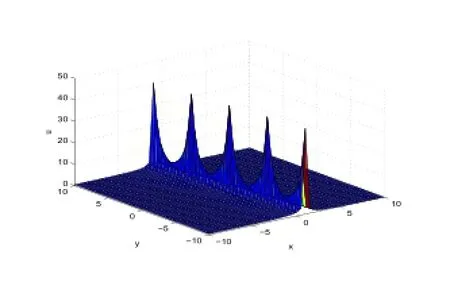
Figure 6:3-dimensional wave of Case (5).

In Figure 5,we taker=-1,β=3,k=3,a0=2,α=-0.7,t=0.1.In Figure 6,we taker=-1,β=-0.3,k=0.1,a0=-0.25,α=-1,t=0.1.

Figure 7:3-dimensional wave of Case (6).

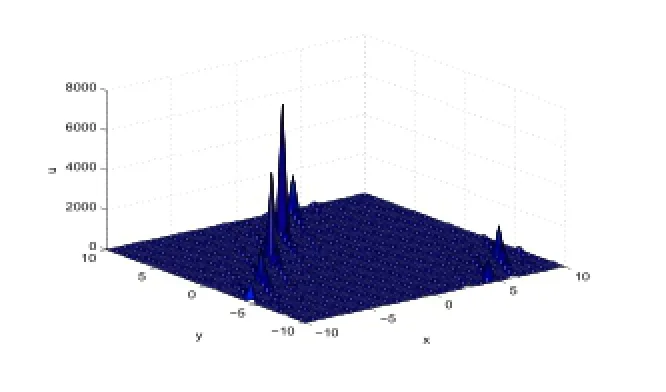
Figure 8:3-dimensional wave of Case (7).

In Figure 7,we taker=-6,β=3,k=2.5,c0=-0.5,α=-2,t=0.1.In Figure 8,we taker=-1,β=3,k=2.9,c0=6,α=-2,c1=2,t=0.1.

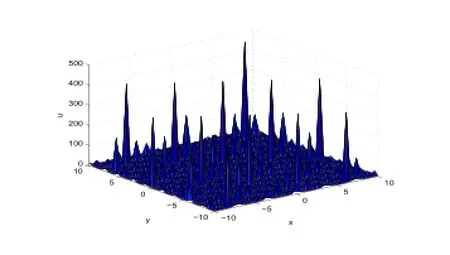
Figure 9:3-dimensional wave of Case (8).

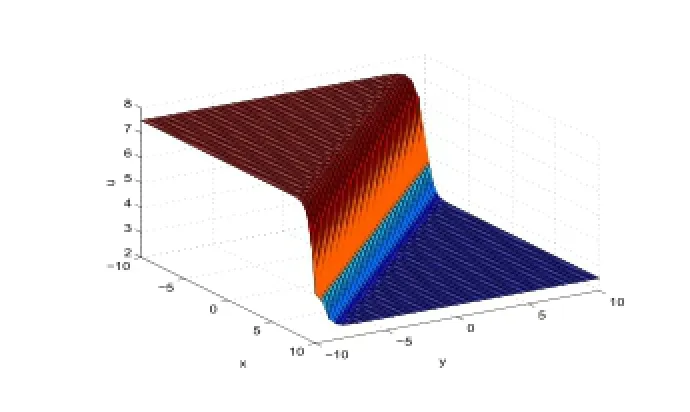
Figure 10:3-dimensional wave of Case (9).

In Figure 9,we taker=-2,β=2,k=1.6,c0=2.5,α=3.2,t=0.1.In Figure 10,we taker=-0.1,β=1,k=1,c0=2.5,α=-1,c1=1,t=0.1.

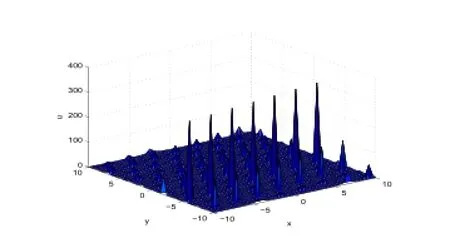
Figure 11:3-dimensional wave of Case (9).

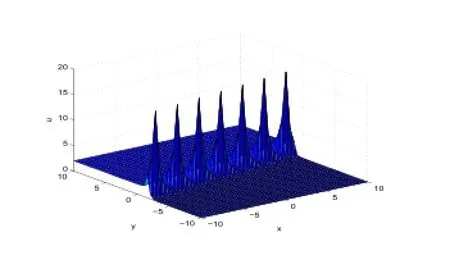
Figure 12:3-dimensional wave of Case (9).

In Figure 11,we taker=-6,β=1,k=-6,c0=1,α=-1,t=0.1.In Figure 12,we taker=6,β=1,k=-6,c0=1,α=-1,t=0.01.

5 Conclusion

In this paper we study the nonlinear Schr¨odinger equation by finding its exact travelling wave solutions through the modified extended tanh method.With the aid of waveform graphs of the solutions,we can obtain the related properties of the equation.In addition,we can also use other methods to obtain the bounded solutions.However,the modified extended tanh method is more concise,more direct and simple than any other existing methods.

[1]Dingjiang Huang,Desheng Li and Hongqing Zhang,Explicit and exact travelling wave solutions for the generalized derivative Schr¨odinger equation,Chaos,Solitons and Fractals,31(2007),586-593.

[2]E.Yomba,The extended Fans sub-equation method and its application to KDV-mKDV BKK and variant Boussinesq equation,Phys.Lett.A,336(2005),463-476.

[3]Abdul-Majid Wazwaz,The Camassa-Holm-KP equations with compact and noncompact travelling wave solutions,Applied Mathematics and Computation,170(2005),347-360.

[4]Z.Y.Zhang,New exact traveling wave solutions for the nonlinear Klein-Gordon equation,Turkish Journal of Physics,32:5(2008),235-240.

[5]V.O.Vakhnenko,E.J.Parkes,A.J.Morrison,A B¨acklund transformation and the inverse scattering transform method for the generalized Vakhnenko equation,Chaos Solitons Fractals,17:4(2003),683-692.

[6]Z.Y.ZhangZ.H.LiuX.J.Miao and Y.Z.Chen,New exact solutions to the perturbed nonlinear Schrodinger’s equation with Kerr law nonlinearity,Applied Mathematics and Computation,216:10(2010),3064-3072.

[7]Z.Y.Zhang,Y.X.Li,Z.H.Liu,et al.,New exact solutions to the perturbed nonlinear Schrdingers equation with Kerr law nonlinearity via modified trigonometric function series method,Communications in Nonlinear Science and Numerical Simulation, 16:10(2011),3097-3106.

[8]S.A.Khuri,A complex tanh-function method applied to nonlinear equations of Schr¨odinger type,Chaos,Solitons and Fractals,20(2004),1037-1040.

[9]Z.Y.Zhang,Z.H.Liu,X.J.Miao,et al.,Qualitative analysis and traveling wave solutions for the perturbed nonlinear Schrodinger equation with Kerr law nonlinearity,Physics Letters A,375:10(2011),1275-1280.

[10]W.Malf l iet,The tanh method:a tool for solving certain classes of nonlinear evolution and wave equations,Journal of Computational and Applied Mathematics,164-165(2004),529-541.

[11]X.J.Miao,Z.Y.Zhang and X.J.Miao,The modifiedG＇/G-expansion method and traveling wave solutions of nonlinear the perturbed nonlinear Schrodinger’s equation with Kerr law nonlinearity,Communications in Nonlinear Science and Numerical Simulation,16:11(2011),4259-4267.

[12]Z.Y.Zhang,X.Y.Gan,D.M.Yu,Bifurcation behaviour of the travelling wave solutions of the perturbed nonlinear Schrodinger equation with Kerr law nonlinearity,Zeitschrift Fur Naturforschung A,66a:12(2011),721-727.

[13]Z.Zhang,Y.H.Zhang,X.Y.Gan,et al.,A note on exact travelling wave solutions for the Klein-Gordon-Zakharov equations,Zeitschrift Fur Naturforschung A,67:3-4(2012),167-172.

[14]Engui Fan,Y.C.Hon,Applications of extended tanh method to special types of nonlinear equations,Applied Mathematics and Computation,141(2003),351-358.

[15]Z.Zhang,F.L.Xia,L.I.Xin-Ping,Bifurcation analysis and the travelling wave solutions of the Klein-Gordon-Zakharov equations,Pramana,80:1(2013),41-59.

[16]A-M.Wazwaz,The tanh and the Sine-Cosine methods for the complex modified KdV and the generalized KdV equations,Computers and Mathematics with Applications, 49(2005),1101-1112.

[17]Z.Zhang,J.Huang,J.Zhong,et al.,The extended(G＇/G)-expansion method and travelling wave solutions for the perturbed nonlinear Schrodingers equation with Kerr law nonlinearity.Pramana,82:6(2014),1011-1029.

[18]L.Kavitha,N.Akila,A.Prabhu,O.Kuzmanovska-Barandovska and D.Gopi,Exact solitary solutions of an inhomogeneneous modified nonlinear Schr¨odinger equation with competing nonlinearities,Mathematical and Computer Modelling,53(2011),1095-1110.

(edited by Liangwei Huang)

∗Manuscript received

†Corresponding author.E-mail:xiaoheng189@126.com.