某高校校内长椅分布优化模型*

2016-04-15王仁举巴焱焱安璐珂徐涛赵晨旭新乡学院数学与信息科学学院河南新乡453003

高教学刊 2016年6期

王仁举　巴焱焱　安璐珂　徐涛　赵晨旭（新乡学院数学与信息科学学院，河南新乡453003）

某高校校内长椅分布优化模型*

王仁举巴焱焱安璐珂徐涛赵晨旭
（新乡学院数学与信息科学学院，河南新乡453003）

摘要：以某高校校内长椅分布优化为研究对象，采用调查问卷的形式获取数据，建立长椅分布的满意度，采用层次分析法，利用Matlab编程计算各区域长椅需求量权重，引入长椅覆盖率α、重叠率β、合理度ξ及使用率ρ等为约束条件，将长椅分布现状图和优化后分布图进行对比，给出了较为合理的优化设置建议。

关键词：层次分析法；优化模型；Matlab；覆盖率；合理度

Abstract:In order to optimize the distribution of benches in the campus of university and by using the method of questionnaire, this paper establishes the satisfaction degree of bench distribution, adopts the analytic hierarchy process, calculates the weight of the bench demand with Matlab programming and introduces constraint condition such as bench coverage rate α, bench overlapping rate β, rationality ξ and usage rate ρ. Based on the comparison between the existing distribution diagram and the optimized distribution diagram, this paper also provides rational suggestions for bench distribution optimization in colleges and universities.

Keywords:analytic hierarchy process; optimization model; Matlab; coverage rate; reason able degree

前言

为了方便师生休息，高校经常在校内场所，譬如：学生宿舍、操场、篮球场、文化广场以及绿化景观带等处设置休闲长椅。然而这些长椅的设置的位置以及数量不尽合理。鉴于此，我们着眼建立模型对校园内长椅位置分布及数量分步进行合理优化，为后勤管理部门更好设置长椅提供参考建议。

一、假设和符号说明

模型假设：

（1）长椅的选址只受人流量、场所空间、场所环境这三个因素影响。（2）用于描述数量和空间分布的合理度ξ超过60%即为合理。

符号说明（见表1）：

表1　符号说明表

二、模型的建立与求解

（一）层次结构模型的建立[3]

Step1：建立层次结构模型

一般分为三层，从上往下数：

第一层为目标层：一般只有一个元素，同时也是分析整个问题的预设目标；第二层为准则层：是为了达到预设目标所涉及的中间所有环节，由多个因素构成，包含所有需要考虑的准则或子准则；第三层方案层：是为了达到预设目标的一些可供选取的每种措施及决策方案。

综合分析学生对校园长椅分布满意度调查表，我们建立层次结构模型，结构图如图1。

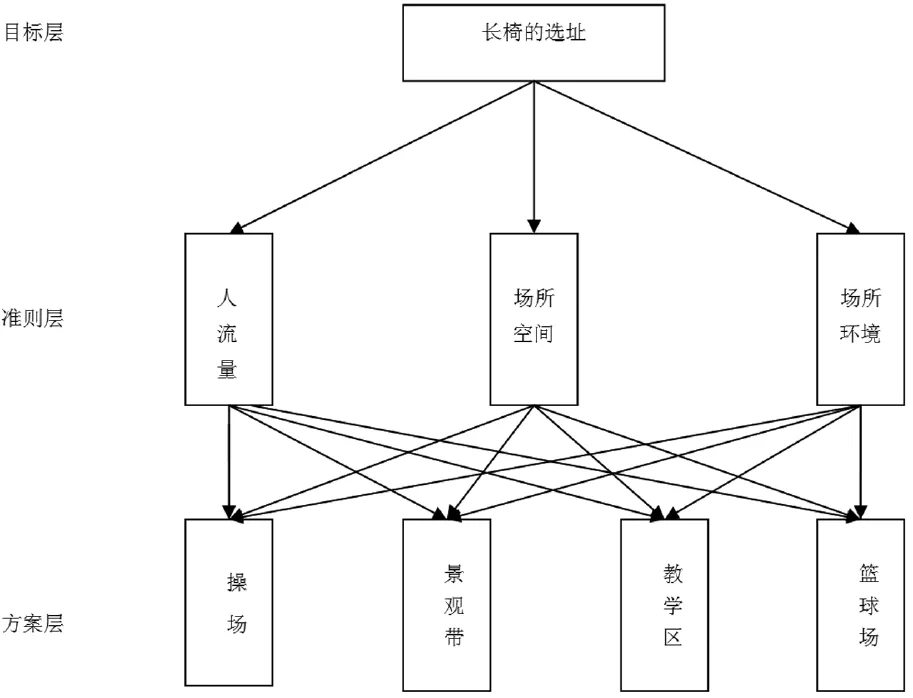
图1　层次结构图

Step2：构造成对比矩阵

应用1～9标度法（表2）构造成对比较矩阵，结合分层结构模型的建立，准则层有人流量，场所空间，场所环境三个指标，利用标度法对其两两指标之间进行比较可以确定该层各指标相对于目标层所占的比重（即把三个指标对目标层的影响程度排序）。将准则层的三个指标对目标层长椅的选址影响两两比较的结果做成表格，如表3。

2，4，6，8表示第i个因素相对第j个因素的影响介于上述两个相邻等级之间。

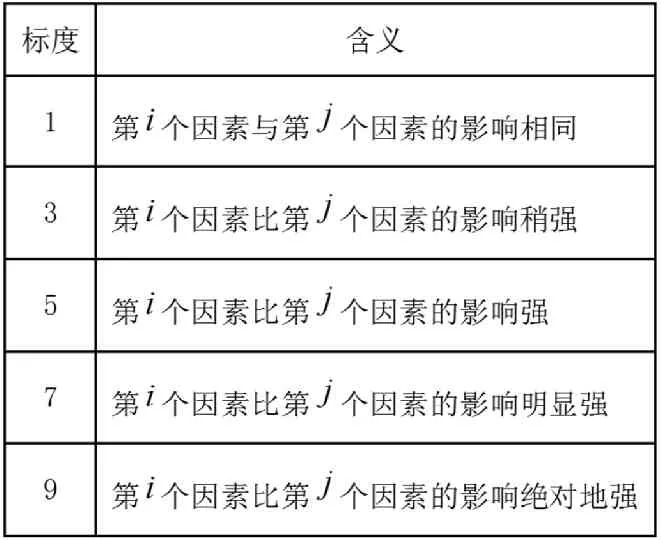
表2　比较标度表

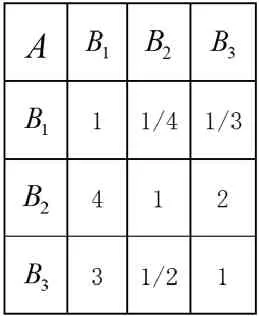
表3　三个指标对长椅选址的影响两两比较结果

由表3可以得到成对比较矩阵为：

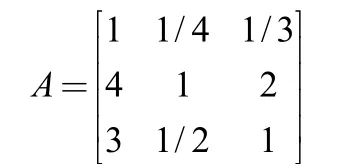
方案层为操场、景观带、教学区、篮球场4个区域场所，相对于上层即准则层每一个指标（人流量，场所空间，场所环境），4个区域两两进行比较后，得到3个成对比较矩阵，为Bi（i=1，2，3）。B1对应的准则层指标为人流量；B2对应场所空间；B3对应场所环境。其两两比较结果可以得到其成对比较矩阵分别为：

Step3：层次单排序及一致性检验

层次单排序：确定下层各因素对于上层某因素影响程度的过程，用权值表示影响程度。

随机一致性指标：定义RI为成对比较矩阵的一致性指标之和与成对比较矩阵的个数之比。对n=1，2，3…，9，给出了RI的值。

表4　随机一致性指标RI的数值

Step4：层次总排序及一致性检验

由一致性检验结果可以认为分配指标体系的各属性指标在总从要求原则的前提下给出的权重的方法可行[1]。

对CR＜0.1进行检验。若通过检验，则可以按照能够排序权向量表示的结果进行决策，否则需要重新考虑模型或者重新构造一致性比较率CR较大的成对比较矩阵。最后按照总排序权向量表示的结果进行排序。

（二）模型的求解

利用Matlab软件对成比较矩阵A求得：λmax=3.0138，ωA= （0.1226，0.5571，0.3202），CI=0.0092，CR=0.0158，通过一致性检验；

对成对比较矩阵B1求解得：λmax=4.0206，wB1=(0.2391，0.08 90，0.2391，0.4328)，CI=0.0069，CR=0.076，通过一致性检验；

对成对比较矩阵B2求解得：λmax=4.0458，wB2=(0.1202，0.45 66，0.2020，0.2212)，CI=0.0153，CR=0.0170，通过一致性检验；

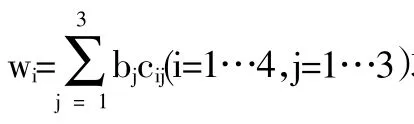
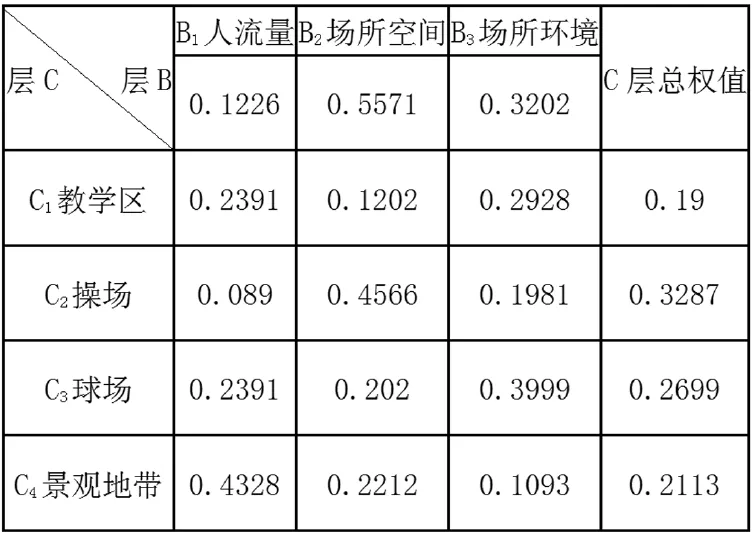
表5　第一个模型计算出各个场所的权重

对层次总排序做一致性检验，如果C层次若干因素对于上一层次某一因素Bj的单排序一致性检验指标为CIj，相应的平均随机一致性指标为RIj，则C层总排序随机一致性比率为：

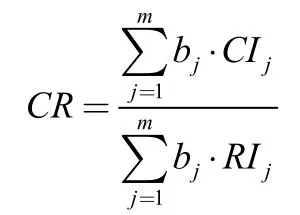
可以得到CR=0.04169＜0.1，通过一致性检验[2]。

因此方案2号区域在长椅选址中占的权重最大，方案3号次之，方案4号再次之，方案1号所占权重最小。所以在长椅的设置分布过程中，应根据各方案区域所占的权重大小对长椅的数量合理布置及分配。

（三）长椅摆放评价模型的建立

为了描述长椅的覆盖率，我们引入了服务半径的概念。长椅的服务半径以长椅为圆心，半径为让r的圆内的人们休息的地方。在该模型内，可以将长椅的服务半径视为以长椅为中点，长度为2r的线段，如图2所示，线段AB即为长椅的范围。

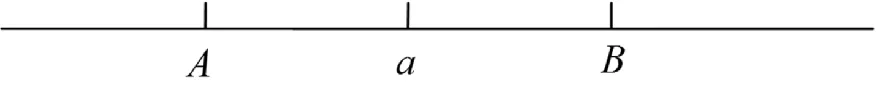
R大，则代表长椅服务范围越大，人们需要走更远的路才能休息，对人们越不方便。为了在一定程度上方便人们，经调查得到，大多数人认为长椅的服务半径r0为20米时，对人们是较为方便的，否则会给人们带来不便。

为了描述长椅的服务范围的覆盖程度，我们引入覆盖率：

易知：0≤α≤1，且当α=1时，覆盖率达到100%，此时覆盖效果最好。但是由于相邻的长椅服务范围可能发生重叠，致使长椅的利用率不高，为了描述它，我们引入重叠率：

易知：0≤β≤1，且当β=0时，所有长椅的服务范围均不发生重叠，此时长椅的利用率达到最大。

1.问题二模型的求解与评价[4]

对校园内运动场所（篮球场，网球场，操场）的长椅配置的评价仅对长椅的摆放距离和数量是否合理进行评价不考虑人流量和活动场地的影响。校园中运动场所的长椅分布如图3。

图3　运动场所的长椅分布图

由图中整体标记的点可以看出，仅计算校园部分活动场所长椅间的平均距离为，长椅间距的标准方差σ=17.13。对部分来讲还可以，但若整体计算长椅间的距离对研究无意义（误差太大）。故运动场所的长椅分布不太合理，需要重新调整。

针对校园内绿色景观带附近以及教学区，仅有极少的长椅放置（校园湖内侧边），长椅摆放距离过近、长椅数量少，以至于长椅不能充分利用，所以长椅的分布严重不平衡，需要添加长椅并重新摆放。

（1）对校园内长椅整体评价

总体上考虑长椅的分布，以及长椅的服务覆盖率和服务重叠率为指标进行评价。长椅的服务覆盖率α越大且重叠率β最小，则长椅最合理。由图3中给出的长椅的位置以及服务半径经计算得出：长椅服务覆盖率：α=9.5%；长椅服务重叠率：β=1.2%。

由上述数据可以得出：对整个校园来讲，长椅的覆盖率非常小，可知长椅配置非常少。所以适当的增加长椅，当运动场所长椅的服务半径为15米，长椅的覆盖率不高且存在重叠率，为了让长椅得到充分利用，并满足人们的需要，因此我们需要对长椅数量及其摆放重新进行分配。

（2）结合人流量对长椅配置进行评价

根据问题要求需要定义一个在一定区域内与长椅使用率与长椅距离有关的指标。

在不考虑天气好坏因素，不考虑放假的因素，根据调查研究所得数据，假设每个长椅使用率相同，由第一模型计算出各个场所权重。取λ=0.2时，计算可得现在长椅摆放的满意度为：ξ=0.58，得出长椅摆放不合理，有待进一步优化。

2.长椅配置优化模型

一般情况下，长椅的使用长度不可能全部被利用，长椅的使用率ρ，经调查研究确定ρ=0.8。

根据表5中权重，综合考虑校园的人流量、校园内各个场所的权重、长椅的服务范围，可得：

计算结果见表6。

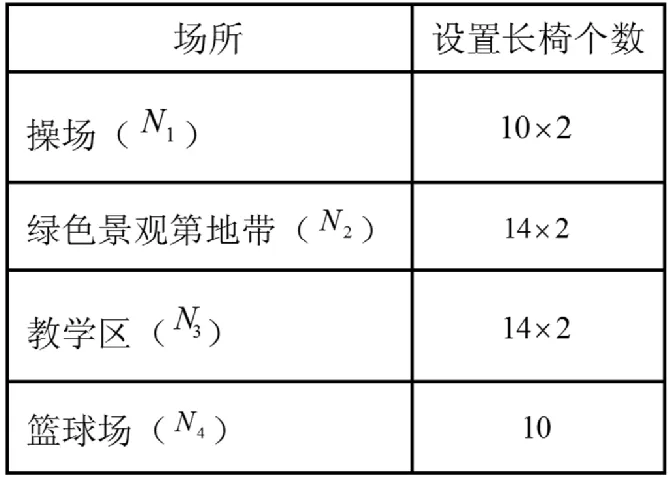
表6　各城所设置长椅数量表

对整个校园的长椅进行优化配置，校园内长椅摆放要在不影响交通的情况下尽可能均匀摆放。

图4　优化后的校园的长椅分布示意图

提示：在图中标记的点中，较大的点可以考虑建成亭子。

（四）模型的检验

由优化后的长椅分布图可以看出：长椅大部分分布在场所和绿色景观带的周边，同时也是人流量较大的地方。用问题分析模型对优化后的长椅分布进行检验。校园长椅间的平均距离为di= 40，方差σ1=8.6，固校园内长椅的摆置相对是合理的，由于考虑校园内建筑物，交通等因素，致使摆放距离以及疏密程度会受到相应的影响。

综合考虑人流量、场所空间、场所流量等因素，经计算可得长椅的配置的合理度为：ξ=0.74；长椅服务覆盖率：α=36.1%；长椅服务重叠率：β=1.0%。

综合考虑上述指标，虽然倡议覆盖率未达到最大值，但是可以看出优化后长椅摆放相对原来更为合理。