基于压力相移辅助的超流体陀螺
2016-04-15方明星杜友武
郑 睿,赵 伟,方明星,杜友武
(1. 安徽师范大学 物理与电子信息学院,芜湖 241000;2. 东南大学 仪器科学与工程学院,南京 210096;3. 南京航空航天大学 导航研究中心,南京 210016)
基于压力相移辅助的超流体陀螺
郑 睿1,2,赵 伟3,方明星1,杜友武1
(1. 安徽师范大学 物理与电子信息学院,芜湖 241000;2. 东南大学 仪器科学与工程学院,南京 210096;3. 南京航空航天大学 导航研究中心,南京 210016)
超流体陀螺是新一代惯性传感器,面临的关键问题是:在幅值锁定控制系统中,热相移的注入存在较大延时,引起其动态测量性能急剧下降。为此,在研究了超流体压力相移产生原理的基础上,提出采用静电力产生压力差的方法,并根据超流体的理论,构建了压力相移的数学模型。为解算角速度,提出了基于压力相移辅助的算法,锁定了超流体相移。仿真结果表明,基于该方法,超流体陀螺测量角加速度变化的信号时,测量误差减小了约一个数量级。因此,超流体陀螺的动态性能得到了很大改善,测量精度有了显著提高。
超流体陀螺仪;压力相移;动态测量误差;惯性传感器
陀螺仪是惯性导航系统的核心传感器,用于敏感运动载体相对惯性空间角运动,其精度对惯性导航系统的精度有决定性作用[1]。基于超流体氦4物质波萨格纳克效应,超流体陀螺具有实现超高精度陀螺仪的潜力,其测量精度理论上可达的数量级[2-3],其今后有望应用于宇航、深空探测、核潜艇等具有长期高精度要求的领域[4-6]。
角速度测量范围是陀螺仪重要的性能指标,称为陀螺仪的量程。超流体陀螺发展之初主要面临量程过小问题。文献[7]的研究表明,由于超流体陀螺的工作曲线(旋转通量与总流量幅值之间的关系曲线)呈现周期性变化,使得其有效的量程仅为 10−5rad/s 的数量级。为了扩展超流体陀螺的量程;文献[8]基于热相移注入技术,提出了基于热相移辅助的超流体陀螺,使得超流体陀螺的量程得到了扩展。
但是,由于加热量不能瞬间达到设定值,热相移注入的实时性不好[2]。从控制系统的角度来说,热相移的延时也就是给系统增加了惯性环节,使得超流体陀螺在测量变角加速度信号时出现了较大的误差。因此,基于热相移辅助的超流体陀螺面临动态测量过程中性能急剧下降的关键问题。
为了消除动态测量误差,需要研究不依赖热相移辅助的新型超流体陀螺。为此,本文研究了压力相移产生的原理,提出了基于压力相移辅助的新型超流体陀螺,解决了超流体陀螺动态测量误差大的问题,对于开发其高测量精度的潜力有重要意义。
1 基于热相移辅助的超流体陀螺的动态测量误差分析
基于热相移辅助的超流体陀螺的结构和如图1所示:环形腔内充满超流体氦 4;“×”的位置表示由数千个孔径为几十纳米的微孔组成的弱连接;薄膜与弱连接组成了内腔,其余部分为外腔;R1和R2是热阻。

图1 基于热相移辅助的超流体陀螺结构图Fig.1 Structure of superfluid gyroscope aided by thermal phase shift
控制图1中热阻R1的加热量,使得弱连接两侧产生化学势能差,超流体在弱连接处发生约瑟夫森效应,产生两路物质波I1=Ic1sin(Δφ1)=Ic1sin(2πfJt1)和I2=Ic2sin(Δφ2)=Ic2sin(2πfJt2)[3],其中,I为流过弱连接超流体的质量流量,Ic为I的最大值,fJ是约瑟夫森频率,t是时间,Δφ1和Δφ2表示两个弱连接两侧的相位差。由图1可知,环路中总流量It等于I1与I2之和,总流量呈现正弦规律变化,总流量幅值Im为[2]
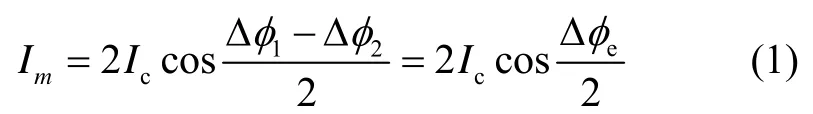
式中:Δφe=Δφ1-Δφ2表示超流体相移;Im可通过检测图1中薄膜的位移而获得。
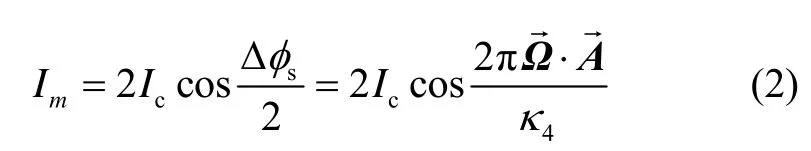
h是普朗克常→数,m4是4He原子质量。由式(2)可知,角速度矢量与总流量幅值Im之间呈现周期性变化,因此使得超流体陀螺的量程很小。为了扩展超流体陀螺的量程,基于热相移注入技术,利用图1中热阻R2加热产生热相移Δφh,这时超流体相移由萨格纳克相移和热相移共同组成:

因此只要控制热阻R2注入热相移,就可以使得Δφe保持恒定,从而锁定超流体陀螺的工作点,扩展超流体陀螺的量程。
基于热相移辅助,超流体陀螺的量程得到了扩展。但是由于加热量不能瞬间达到设定值,因此热相移是不能实时注入的[2,9]。具体来说,在图1中对热阻2进行加热时,加热量需要历经几十毫秒过程。因此当角加速度变化时,热相移发生了变化,造成超流体的相位不能得到及时补偿,使得陀螺出现了很大的误差;而角加速度恒定时,热相移也保持恒定,陀螺的输出基本没有误差。从控制的角度来说,热相移的延时相当于在控制系统中加入了惯性环节,减小了系统阻尼,会引起系统输出振荡。文献[8][10]的研究验证了这一点,超流体陀螺可以高精度测量加速度恒定的角速度,但角加速度发生变化时,超流体陀螺的输出出现了较大的误差。因此,基于热相移辅助的超流体陀螺面临动态测量过程性能急剧下降的关键问题。
2 超流体陀螺的压力相移辅助算法
为了消除动态测量的误差,需要研究不依赖热相移辅助的新型超流体陀螺。
超流体由普通流体成分和超流性成分共同构成,超流体相位的梯度与超流性成分的速度成正比[2]:

式中:m4为氦4原子质量,h是普朗克常数,vs为超流体成分的速度。由式(4)可知,若要产生超流体相移,需要使得超流性成分运动起来。
为了使超流性成分运动,通常采用在超流体内部构建温度差和压力差两种方式,其中构建温度差产生的即为热相移,它并不能实时注入。根据参考文献[8]可知,采用静电力吸引薄膜的方式可以瞬态在超流体内产生压力差。因此为了产生压力相移,首先需要研究超流体压力差的产生方法。
2.1 超流体压力差的产生方法
根据参考文献[8]的思想,本文提出采用静电力吸引薄膜的方式产生压力差。根据薄膜运动的状态,分三种情况进行讨论,如图2所示。

图2 超流体压力差的产生示意图Fig.2 Generation of superfluid pressure differential
图2中,薄膜的表面涂有一层金属,在电极上施加电压,使电极与薄膜表面的金属之间产生静电力Fe。由于静电力吸引薄膜,因此其方向朝上。当薄膜位移向上偏离其平衡位置时,胡克力kx的方向朝下,其中,k是胡克系数,x是薄膜偏移平衡位置的位移。除受到静电力和胡克力,薄膜还受到超流体压力ΔPAd的作用,Ad表示薄膜表面积。dx/dt表示薄膜的运动方向,设薄膜向电极方向运动dx/dt为正,反之为负。当dx/dt为零、大于零和小于零时,薄膜受到的超流体压力不同,因此薄膜受力分三种情况分析:

在这种情况下薄膜处于静止状态,无超流体流过弱连接,因此此时压力差ΔP=0。在这种情况下,薄膜仅受静电力和胡克力,根据薄膜受力情况分析可得:
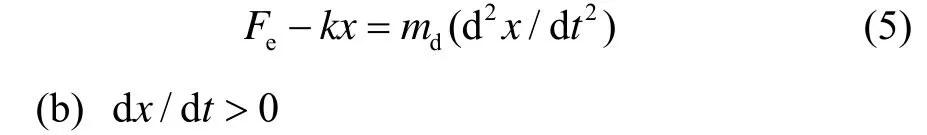
在这种情况下,薄膜处于向着电极方向运动的状态,由于外腔的体积呈减小趋势,内腔的体积呈增大趋势,因此外腔的压力高于内腔的压力,即ΔP>0。根据薄膜的受力情况分析可得:
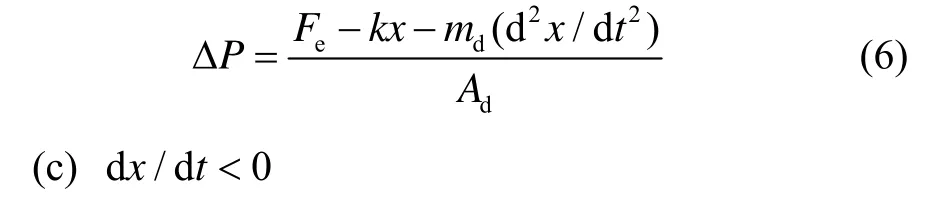
在这种情况下,薄膜处于向着电极的反方向运动的状态,由于外腔的体积呈增大趋势,内腔的体积呈减小趋势,因此外腔的压力低于内腔的压力,即ΔP<0。根据薄膜的受力情况分析可得:
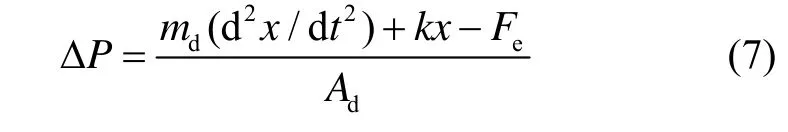
根据上述分析可知,在dx/dt≠0的情况下,可在内外腔之间产生压力差。以下通过分析压力差作用下超流体的运动情况,构建压力相移的数学模型。
2.2 压力相移数学模型的构建
根据超流体的二流体理论,压力差只能引起普通流体成分运动,而无粘性的超流性成分则不会直接因此而流动。具体来说,图2(b)中,由于外腔压力大于内腔压力,普通流体成分由外腔流入内腔,形成vn;图2(c)中,由于外腔压力小于内腔压力,则普通流体流动的方向正好相反。vn与压力差ΔP之间的关系为[11]

式中:η为超流体粘度,l表示腔体长度,R表示腔体直径。由于普通流体成分流动和超流体流动存在相互的关系,常流体的流动vn会导致超流体逆向流动,因此在图 2(b)、2(c)中,普通流体成分流入、流出内腔会引起超流性成分流出、流入内腔,形成超流性成分vs。vn与vs之间遵循质量守恒[12]:

式中:ρn和ρs分别为常流体密度和超流体密度。根据式(3)(8)(9)可得,压力相移Δφp为

式中:压力相移Δφp只与压力差以及系统的结构参数有关,构成了压力相移的数学模型。
2.3 超流体陀螺角速度的测量值
在构建了压力相移数学模型的基础上,可采用类似于热相移辅助的方法:通过注入压力相移,实时抵消萨格纳克相移Δsφ变化,从而锁定超流体相移,即

此时,由式(3)和式(11)可知,超流体陀螺的角速度测量值dΩ为

3 实现方案研究与仿真分析
为检验该方法的有效性,本文设计了该方法的实现方案并进行了仿真分析。
3.1 实现方案
基于压力相移辅助超流体陀螺方案如图3所示。

图3 基于压力相移辅助的超流体陀螺实现方案示意图Fig.3 Scheme for superfluid gyroscope aided by pressure phase shift
图3装置内白色的部分充满超流体。压力相移产生的方法是:采用电极吸引薄膜产生超流体压力差,从而产生压力相移。薄膜4的运动方向设置为dx/dt>0,薄膜5的运动方向设置为dx/dt<0,这样在微孔7和微孔8处即可产生方向相反的压力相移。
在压力相移产生的基础上,基于压力相移辅助的超流体陀螺研究方案是:通过热阻加热,双弱连接两侧产生化学势能差,超流体在双弱连接处发生约瑟夫森效应,产生两路超流体物质波。薄膜6的表面附有稀土金属(可产生磁场),当薄膜 6的位移变化时,磁场相应地变化,超导量子干涉仪检测磁场的变化测量薄膜4的位移。这样,角速度会引起两路物质波产生干涉,引起薄膜位移幅值变化,将该幅值与参考幅值比较,处理器的输出控制电极9和电极10的电压,产生压力相移,锁定超流体幅值,并且解算角速度。
3.2 仿真分析
根据上述实现方案,对基于压力相移辅助的超流体陀螺以及基于热相移辅助的超流体陀螺同时开展仿真实验。仿真参数设置如下:
1)结构参数[2]:面积矢量大小A=5×10-4m2,弱连接处的微孔数量N=4225,微孔孔径d=7×10-8m ,管路长度l =2.5×10-2m2,管路直径R=5×10-3m ,薄膜面积Ad=5×10-5m2;
2)工作参数[2]:工作温度T=2.169K,流过弱连接处的流量幅值Ic=4.5×10-12kg/s;约瑟夫森频率fJ=700Hz,热相移延时时间20ms,压力相移延时时间1ms,超流体陀螺系统噪声
3)输入角速度:设置两种典型的输入角速度。①先加速,后匀速,再加速:0到0.1 s时,角加速度为0.01 rad/s2;0.1 s到0.2 s时,保持恒定;0.2 s到0.3 s时,角加速度为0.01 rad/s2。②正弦规律变化:幅值为0.001 rad/s,频率为10 Hz。
按上述两种角速度输入方式,对基于热相移辅助和基于压力相移辅助的超流体陀螺的工作过程进行仿真,仿真结果曲线如图4和图5所示。
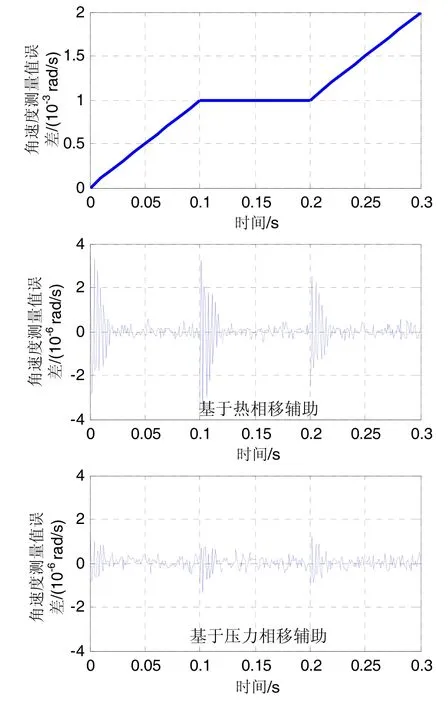
图4 角速度加速但中间匀速时超流体陀螺测量误差曲线Fig.4 Detection errors of superfluid gyroscope when angular velocity accelerates except moving uniformly in middle period

图5 角速度呈正弦规律变化时超流体陀螺的测量误差曲线Fig.5 Detection errors of superfluid gyroscope when angular velocity is sinusoidally changed
由图4 可知,基于热相移辅助,由于系统噪声的存在,超流体陀螺的角速度测量值总体上呈现出10-7rad/s数量级的误差。但在0 s、0.1 s、0.2 s时,即在角加速度发生变化的时刻,角速度测量值出现了最大3.2×10-6rad/s 的动态测量误差,该误差在0.02 s的时间内逐渐衰减到正常值。基于压力相移辅助,角速度测量值误差总体上同样为数量级。在角加速度发生变化的时刻,角速度测量值的误差略有增大,其最大值约为6.7×10-7rad/s ,与超流体陀螺系统噪声产生的误差在同一个数量级。
由图5可知,当角速度正弦规律变化时,其角加速度是时变的。基于热相移辅助,角速度测量值总体上呈现标准偏差为2×10-6rad/s的误差。而基于压力相移辅助,角速度测量值总体上呈现标准偏差为3×10-7rad/s的误差,仅为热相移辅助时的1/7。
根据以上分析可知,基于压力相移辅助,超流体陀螺的动态测量误差得到了明细改善,角速度测量值更加接近于真实值。
4 结 论
针对基于热相移辅助的超流体陀螺存在动态性能急剧下降的问题,本文研究了压力相移产生的原理,构建了压力相移的数学模型,提出了基于压力相移辅助的算法。仿真结果表明,基于压力相移辅助,超流体陀螺测量角加速度变化的信号时,测量误差减小了约一个数量级。因此,超流体陀螺的动态性能得到了极大改善,可使超流体陀螺应用在各种领域,发挥其超高测量精度的优势。
(References):
[1] 王巍. 惯性技术研究现状与发展趋势[J]. 自动化学报, 2013, 39(6): 723-729. Wang Wei. Status and development trend of inertial technology[J]. Acta Automatica Sinica, 2013, 39(6): 723-729.
[2] Sato Y, Parkard R. Superfluid Helium quantum interference devices: physics and applications[J]. Rep. Prog. Phys., 2012, 75: 016401.1-016401.27.
[3] Golovashkin A I, Zherikhina L N, Tskhovrebov A M, et al. Ordinary SQUID interferometers and superfluid helium matter wave interferometers: The role of quantum fluctuations[J]. Journal of Experimental and Theoretical Physics, 2010, 111(2): 332-339.
[4] Zheng R, Zhao W, Liu J Y, et al. Mathematical model of 4He quantum interferometer gyroscope[J]. Transactions of Nanjing University of Aeronautics and Astronautics, 2012, 29(4): 360-366.
[5] 郑睿, 赵伟, 刘建业, 等. 随机振动引起的超流体陀螺特性[J]. 中国惯性技术学报, 2013, 21(6): 797-802. Zheng Rui, Zhao Wei, Liu Jian-ye, et al. Research on characteristic of superfluid gyroscope noise caused by random vibration[J]. Journal of Chinese Inertial Technology, 2013, 21(6): 797-802.
[6] Narayana S, Sato Y. Superfluid quantum interference in multiple-turn reciprocal geometry[J]. Physical Review Letters, 2011, 106(6): 255301.1-255301.4.
[7] Xie Z, Liu J Y, Zhao W, et al. The exploratory research of a novel gyroscope based on superfluid Josephson effect [C]//PLANS 2010 Conference. 2010: 14-19.
[8] Joshi A, Packard R. A continuously operating, flux locked, superfluid interferometer[J]. Journal of Low Temperature Physics, 2013, 172(1): 162-174.
[9] Narayana S, Sato Y. Quantum coherence in a superfluid Josephson junction[J]. Physical Review Letters, 2011, 106(4): 055320.1-055302.4.
[10] 聂威, 赵伟, 郑睿, 等. 基于模糊控制器的热相移辅助超流体陀螺研究[J]. 航天控制, 2014, 32(1): 21-25. Nie Wei, Zhao Wei, Zheng Rui, et al. Research on superfluid gyroscope aided by heat phase shift based on fuzzy-PID [J]. Aerospace Control, 2014, 32(1): 21-25.
[11] Landau L D, Lifahitz E M. Fluid mechanics[M]. Pergamon Press, 1959: 507-508.
[12] Narayana S, Sato Y. Heat flux manipulation with engineered thermal materials[J]. Physical Review Letters, 2012, 108: 214303.1-214303.5.
Superfluid gyroscope aided by pressure phase shift
ZHENG Rui1,2, ZHAO Wei3, FANG Ming-xing1, DU You-wu1
(1. College of Physics and Electronic Information, Anhui Normal University, Wuhu 241000, China; 2. School of Instrument Science and Engineering, Southeast University, Nanjing 210096, China; 3. Navigation Research Center, Nanjing University of Aeronautics and Astronautics, Nanjing 210016, China)
The superfluid gyroscope, as a matter-wave interferometric gyroscope, faces the problem that the injecting of the thermal phase shift has large latency when aided by amplitude locking, which can rapidly degrade the dynamic performance of the superfluid gyroscope. To solve this problem, a pressure phase shift method is presented for the gyroscope, which uses electrostatic force to produce the pressure difference. The mathematic model of pressure phase shift is established based on the superfluid theory. In order to calculate the angular velocity, an algorithm aided by pressure phase shift is presented to lock the superfluid phase shift. Simulation results indicate that, by using the proposed method to measure the signals with varied angular acceleration, the measurement error is decreased by nearly one order of magnitude, and the dynamic performance and detection accuracy of the superfluid gyroscope are significantly improved.
superfluid gyroscope; pressure phase shift; dynamic measurement error; inertial sensor
U666.1
:A
2016-07-03;
:2016-11-04
国家自然科学基金(61074162);高等学校省级自然科学研究项目(sjky2015015,KJ2016A698);安徽师范大学博士科研启动基金(2014bsqdjj37);安徽师范大学校创新基金(2015cxjj14)
郑睿(1980—),男,博士后,副教授,硕士生导师,研究方向为高精度惯性传感器。Email: zrwx0609@nuaa.edu.cn
1005-6734(2016)06-0798-05
10.13695/j.cnki.12-1222/o3.2016.06.018
