旋转式重力梯度测量系统试验及数据处理
2016-04-15李海兵周坚鑫马存尊
李海兵,郭 刚,周坚鑫,马存尊,丁 昊
(1. 北京航天控制仪器研究所,北京 100039;2. 国土资源航空物探遥感中心,北京 100083)
旋转式重力梯度测量系统试验及数据处理
李海兵1,郭 刚1,周坚鑫2,马存尊1,丁 昊1
(1. 北京航天控制仪器研究所,北京 100039;2. 国土资源航空物探遥感中心,北京 100083)
旋转式重力梯度测量系统采用旋转调制方式求取重力梯度信息。首先,从旋转加速度计的基本原理出发,给出了重力梯度测量系统的主要工作模式;其次,构建了旋转加速度计重力梯度测量系统组成和主要功能模块,提出了采用引力产生装置开展实验室引力梯度测量的试验方案;最后,给出了旋转加速度计重力梯度测量系统的静态梯度试验验证基本条件、试验设备,并开展了重力梯度测量试验。试验结果表明,旋转式重力梯度测量系统在实验室条件下完成引力梯度试验,该系统可以检测优于200 Eu(1 Eu=10-9/s2)的引力梯度,该系统开展的试验验证为动态重力梯度仪的研制奠定了基础。
重力梯度仪;高精度加速度计;引力产生装置;重力梯度试验;旋转调制
旋转式重力梯度仪是在动基座重力仪难以完成重力测量的背景下提出的,最初用于军事用途,研制成功后一直装备于美国海军的舰艇上。2000年之后,在澳大利亚BHP公司的努力下,成功研制出FALCON™航空重力梯度仪,并成功用于资源勘探。至此重力梯度仪技术逐渐成为地球物理研究、资源勘探领域的新兴技术手段,其基于飞机等运载平台的动基座勘查方式具有效率高、成本低、环境适应性强的优点,可以在人员难以到达的复杂地理环境中部署使用。国外,如全张量重力梯度仪 Air-FTG™、部分张量重力梯度仪FALCON™等,都已经在航空重力梯度勘查领域表现出良好的性能[1-3]。近年来,全世界已有超过十台旋转式重力梯度测量系统陆续投入油气和矿产资源勘探领域中去,并被实践证明是寻找石油、天然气、煤炭和贵金属矿藏的有效工具[3]。
国内外有多家单位开展了旋转加速度计重力梯度仪关键技术的研究[4-12],其中包括误差分析、加速度计及稳定平台的需求分析、加速度计标度系数匹配研究[9]、加速度计测试技术等。本文旨在介绍采用石英加速度计为主要传感器,旋转平台为主要旋转调制装置,微弱信号处理电路为主要检查手段搭建的旋转式重力梯度测量系统,并采用引力产生装置产生的引力加速度(梯度)信息作为系统输入,系统的测量值作为输出,通过实验室试验,比较二者之间关系,以此确定系统的功能和性能指标。
1 旋转加速度计重力梯度仪测量原理
旋转加速度计重力梯度测量系统的本质是对两对以特定方式安装在旋转圆盘上的加速度计输出进行差分的方式间接获得引力梯度或者重力梯度信息。如果这两个加速度计互相匹配,并且共基线是旋转稳定的,那么载体动态所引起的加速度就以共模方式呈现在加速度计的输出中,对输出差分可以消除这个载体的共模加速度成分,从而抑制载体运动加速度的影响,最终得到梯度分量。
为了克服加速度计由于材料和加工精度引起的匹配不一致,实现对微小的重力梯度信号的检测,重力梯度仪在尽可能改善材料稳定性和减小平衡误差的基础上,还通过旋转调制技术使各种输入干扰加速度被调制到同重力梯度信号不同的频率上,从而提高信噪比。如图1所示,旋转加速度计重力梯度测量系统的圆盘上对称安装有4个高精度加速度计,加速度计的输入轴与圆盘的切线平行,相对两个加速度计的指向相反。把相对安装的两个加速度计的输出分别相加,可以抵消载体平动加速度引起的误差;两两相加的结果再相减,就可以进一步抵消载体角加速度引起的误差;最后把圆盘安放在惯性稳定平台内,就可以消除载体向心加速度引起的误差,使圆盘的输出中只剩下重力梯度部分张量的成分。
圆盘旋转时,圆盘中心位置处的重力梯度部分张量和载体的运动加速度就同时被调制到4个加速度计的输出上。成对加速度计检测质量质心之间的距离为2r,旋转速率为ω的圆盘输出为
2 旋转加速度计重力梯度测量系统组成
旋转式重力梯度测量系统主要由高精度石英加速度计、微弱信号处理电路、旋转装置(本系统采用双轴转台)、同步电路、供电系统、数据采集与存储电路、电子线路等部分组成,详见图2所示。
图2中:高精度石英加速度计是测量系统的核心传感器,主要测量检测质量敏感的加速度;旋转装置通过旋转将加速度计的输入加速度调制在与转速对应的频率上,例如转速为90 (°)/s,根据式(1),梯度信息被调制在0.5 Hz上;同步电路为梯度信号的解调提供同步信号;微弱信号处理电路对加速度计的输出信号进行隔直、加法运算、低通滤波、带通滤波、陷波等提高信噪比后,进行解调运算,获得梯度信息对应的电压信号;供电系统主要为加速度计、同步电路和微弱信号处理电路提供低纹波的电压[11];数据采集和存储电路采集和存储微弱电路处理解调后的电压信号;控制柜完成对旋转装置转速的设定和控制;电子线路完成各分系统间电信号的传输。
3 试验验证与数据分析
3.1 试验验证方案
总体思路是采用引力产生装置产生的引力加速度(梯度)信息作为系统输入,系统的测量值作为输出,比较二者之间的关系确定系统的检测能力。
试验验证总体方案如图3所示[13]。试验过程中,在距离系统较近的位置1(称为近点)与较远的位置n(称为远点)之间取n-2个点,引力产生装置质心处在这些点时进行引力梯度的测量;引力产生装置的质心相对坐标原点o处远点位置n时,引力产生装置作用在重力梯度测量系统上的引力梯度记为Γn,引力产生装置质心在位置 1、2、3、…、n-1时产生相应的引力梯度,其值与Γn的差为该点的引力产生装置作用在原点o处的引力梯度。
3.2 引力产生装置引力场的简单近似计算
将引力产生装置作为一个质点,将旋转中心作为一个点。根据万有引力定律,位于(l,0,h)处质量为m的质点作用坐标系xyz原点的引力加速度计:
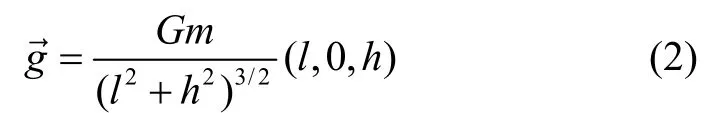
式中:G是万有引力常数。
对表达式(2)求偏导计算,得到(l,0,h)处质量为m的质点作用坐标系xyz原点的梯度分量:

3.3 试验验证
3.3.1 基本试验条件及主要参数
1)引力梯度试验在实验室的隔振地基上进行,环境温度为23°C±3°C,湿度为40%~80%;
2)旋转转速设定值为90 (°)/s;
3)微弱信号处理电路输出模拟电压信号的数据采样频率为25 Hz,分辨率优于0.01 mV;
4)试验方案中采用四只高精度加速度计,其输入轴依次相差90°;
5)位置精度为 1 cm。根据可以移动的最近距离为0.79 m,此时若有1 cm位置精度误差将导致大约30 Eu的梯度误差;
6)成对加速度计检测质量之间的距离为0.4 m。
3.3.2 试验设备及装置
1)电源:供电系统输出电压纹波小于3 mV;
2)引力产生装置:采用球外形,直径为300 mm;
3)高精度旋转装置:转速范围±300 (°)/s,定位精度优于1′,相对速率精度优于10-6。
3.3.3 引力梯度试验及数据分析
根据图 3给出的引力梯度试验方案进行了引力梯度试验。图4为实验室地基上进行引力梯度试验的现场图。

图3 重力梯度测量系统试验方案示意图Fig.3 Experiment scheme of gravity gradient measurement system

图4 引力梯度试验Fig.4 Gravitation gradient experiment in laboratory
图5给出了在近距离点(0.79 m)和远距离点(3.5 m)进行引力产生装置移动试验时系统输出的结果。共进行了超过3 h的试验,引力产生装置共移动7次。近距离点的位置在0.79~0.8 m之间,根据式(3)计算的引力梯度理论值范围是 495~518 Eu,当距离为 1.115 m时,理论值为183 Eu。
在3 h的测试过程中,系统的输出产生了漂移,蓝线是系统的原始输出,红线是经过漂移补偿后的系统输出值。图 5的中图对上图中的原始数据进行了100 s的移动平滑滤波,下图对上图中的原始数据进行了200 s的移动平滑滤波。
通过系统的设计参数,将图5中系统输出原始信号的噪声换算成为引力梯度单位(Eu),并且将100 s移动平滑和 200 s移动平滑后的数据也折合成加速度梯度单位。详见表1所示。
通过表1可知,系统噪声在采样为25 Hz后的最大值为360 Eu,经过100 s和200 s平滑后的最大值分别为254 Eu和158 Eu。对所有远距离点和近距离点时系统的输出值取平均值后求差,可得系统输出在两个点之间由于引力产生装置导致的梯度变化值。原始数据、100 s平滑和200 s平滑后由于引力产生装置位置变化导致的系统变化分别为570 Eu、530 Eu、496 Eu。
根据试验方案图3给出的方法,针对引力产生装置在不同的近距离点上开展了试验,而远距离点仍在3 m之外,试验结果如图6所示。数据处理仍采用取平均值的处理方式,其中蓝线为理论计算值,红线是系统测量值经过平均处理后的值。通过图6的上图可知,当近距离点大于1 m后,系统的输出值基本不变化。

图5 近距离点-远距离点间引力梯度试验结果Fig.5 Results of gravitation gradient experiment between two points with different distances (0.79 m and 3.5 m)

表1 系统近距离点-远距离点系统输出的数据处理结果Tab.1 Output results of gravity gradiometer systems at short- and long-distance points Eu
4 结论及建议
通过在实验室环境下采用4只加速度计旋转调制的技术方案,并采用引力产生装置开展引力梯度试验,可以得出下面给出的结论。
4.1 系统功能
该试验系统通过匀速旋转调制在实验室环境完成完成了引力梯度试验的检测,说明加速度计、微弱信号处理技术、旋转平台、供电系统、电子线路等部分工作正常,方案可行。
4.2 系统检测能力
通过理论计算和引力梯度试验说明,旋转加速度计重力梯度测量系统可以在实验室完成引力梯度试验。经过理论计算,引力产生装置在1.115m的理论值为183 Eu,通过图6可知,实际测试系统在此位置输出为218 Eu的引力梯度。参照国军标GJB1037a-2004中加速度计测试的方法,即输出值与理论值之比大于50%,即可认为系统的分辨率为理论计算值。
通过重力梯度测量原理和加速度计检测质量之间的距离为0.4 m,可以估算加速度计最小可以检测的加速度大约为(1/2)×183×10-9×0.2×(1/9.78)≈1.87×10-9g。

图6 不同距离点上进行引力梯度试验结果Fig.6 Results of gravitation gradient experiment at points with different distances
4.3 建 议
以上试验获得的试验结果需要对系统输出进行平滑等数据处理,要进一步提高系统的检测能力和实时性,需要在加速度计噪声抑制、微弱信号处理电路和系统技术方面进一步加深研究,并且需要进行小型化的研制工作,为重力梯度仪的国产化和实用化奠定基础。另外,由于重力梯度仪测量属于间接测量,需要进一步建立重力梯度测量指标体系。
致谢:特别感谢科技部、国土资源部地质调查局、航天科技九院为本研究提供的研究资金。本项目研究、研制实施过程中,得到了许多帮助,特别感谢东南大学蔡体菁教授在误差分析和测试方面的建议和帮助,感谢国土资源航空物探遥感中心的舒晴、高维、尹航在项目实施中无私的付出。另外,在项目实施过程中有许多同志参与或给出了一些宝贵的建议,在此一并表示感谢,他们是胡宝余、薛正兵、马杰、王晓东、杨慧、卢明涛、常江、赵毅、郭纬川和楚贤。
(References):
[1] Lockheed Martin Gravity System[EB/OL]. [2016/12/1]. http://www.lockheedmartin.com/us/products/gravity-grad iometry.html.
[2] FALCON Gravity Gradiometry[EB/OL]. [2016-12-01]. http://www.cgg.com/en/What-We-Do/Multi-Physics/Acq uisition-Technologies/Falcon-Gravity-Gradiometry.
[3] FALCON Airborne Gravity Gradiometer Survey Targets Outlined, Genesis Property, Saskatchewan[EB/OL]. (2016-08-23)[2016-12-01]. http://www.stockhouse.com/news/ press-releases/2016/08/23/falcon-airborne-gravity-gradio meter-survey-targets-outlined-genesis-property.
[4] Dransfield M H, Christensen A N. Performance of airborne gravity gradiometers[J]. The Leading Edge, 2013, 32(8): 908-922.
[5] Bouman J, Fuchs M J. GOCE gravity gradients versus global gravity field models[J]. Geophysical Journal International, 2012, 189: 846-850.
[6] Johnston P. Self-gradient effects for airborne gravity gradiometry[C]//22nd International Geophysical Conference and Exhibition. Australia, 2012: 1-3.
[7] Justin A R. Gravity gradiometer aided inertial navigation within non-GNSS environments[D]. College Park, MD, USA: University of Maryland, 2008.
[8] O'Keefe G J, Lee J B, Turner R J, et al. Gravity gradiometer. US: No.5922951[P].1999-07-13.
[9] 涂良成, 刘金全, 王志伟, 等. 旋转重力梯度仪的加速度计动态调节方法与需求分析[J]. 中国惯性技术学报, 2011, 19(2): 131-135. Tu Liang-cheng, Liu Jin-quan, Wang Zhi-wei, et al. Methods and requirements of dynamic compensation between acelerometers in rotating gravity gradiometer[J]. Journal of Chinese Inertial Technology, 2011, 19(2): 131-135.
[10] 李海兵, 朱志刚, 魏宗康, 等. 高精度加速度计分辨率的动态估算方法[J]. 中国惯性技术学报, 2012, 20(4): 415-419. Li Hai-bing, Zhu Zhi-gang, Wei Zong-kang, et al. Error analysis on gravity gradiometer of rotating accelerometer [J]. Journal of Chinese Inertial Technology, 2012, 20(4): 415-419.
[11] 李海兵, 杨慧, 马存尊, 等. 用于重力梯度仪系统中的高精度微弱信号检测电路[J]. 中国惯性技术学报, 2013, 21(5): 581-584. Li Hai-bing, Yang Hui, Ma Cun-zun, et al. High precision and week signal detection circuits of gravity gradiometer system[J]. Journal of Chinese Inertial Technology, 2013, 21(5): 581-584.
[12] 钱学武, 蔡体菁. 旋转加速度计重力梯度仪标定方法[J]. 中国惯性技术学报, 2016, 24(4): 427-430. Qian Xue-wu, Cai Ti-jing. Calibration method for gravity gradiometer of rotating accelerometer[J]. Journal of Chinese Inertial Technology, 2016, 24(4): 427-430.
Experiment and data processing for rotating gravity gradient measurement system
LI Hai-bing1, GUO Gang1, ZHOU Jian-xin2, MA Cun-zun1, DING Hao1
(1. Beijing Aerospace Control Device Institute, Beijing 100039, China; 2. China Aero Geophysical Survey and Remote Sensing Center for Land and Resources, Beijing 100083, China)
This rotating gravity gradient measurement system adopts a rotating modulation mode to measure the gravity gradient tensor. First, the operation mode of the gravity gradient measurement system is presented according to the operation principal of the rotating accelerometer gravity gradiometer. Then, the gravity gradient measurement system, its main subsystems and their main functions are introduced, and the gravity gradient test scheme is proposed, which uses gravitation generating device to carry out laboratory gravitation gradient measurement. Finally, its test algorithm is derived, and the static gravitation gradient test experiment devices and conditions in laboratory are given. The gravitation gradient tests are conducted, which show that the detection accuracy of the proposed system is better than 200 Eu (1 Eu=10-9/s2). The experiment verifica- tion by the proposed system lays a foundation for the development of the dynamic gravity gradiometer.
gravity gradiometer; high precision accelerometer; gravitation induced object; gravity gradient test; rotating modulation
U666.1
:A
2016-08-26;
:2016-11-16
国家高技术研究发展计划(863计划)(2011AA060506);航空地球物理探测技术及实用化仪器研发计划项目(科[2012]01-045-008);民用航天专业技术预先研究(D010101);科技部对外科技合作专项;中国航天科技九院创新基金
李海兵(1979—),男,博士,高级工程师,从事重力测量技术研究。E-mail: lanseshuishou@163.com
1005-6734(2016)06-0736-05
10.13695/j.cnki.12-1222/o3.2016.06.007
