陀螺寻北仪中测量信号的在线建模与滤波
2016-04-15王立冬罗贤全梁冠辉
王立冬,王 品,罗贤全,梁冠辉
(1. 军械工程学院,石家庄 050003;2. 武汉军械士官学校,武汉 430075)
陀螺寻北仪中测量信号的在线建模与滤波
王立冬1,王 品2,罗贤全1,梁冠辉1
(1. 军械工程学院,石家庄 050003;2. 武汉军械士官学校,武汉 430075)
针对光纤陀螺寻北仪中光纤陀螺(FOG)和加速度计的随机误差,采用改进型二阶自回归AR(2)模型,在线建立了光纤陀螺和加速度计随机误差模型。根据该模型,建立了FOG陀螺寻北仪的12阶Kalman滤波器,实现了两个 FOG和两个加速度计测量信号在寻北过程中的实时滤波。仿真、Allan方差分析与寻北试验结果表明:FOG信号中随机游走、零偏不稳定性、变化率随机游走、变化率斜坡和量化噪声五项噪声源误差系数都小于滤波前的二分之一;在减小光纤陀螺和加速度计测量信号中的随机误差,提高其精度的同时,FOG寻北仪的寻北误差减小了0.3 mil。
光纤陀螺寻北仪;加速度计;改进型AR(2)模型;Kalman滤波
陀螺寻北一般采用陀螺和加速度计,通过多位置方式静态寻北。陀螺仪和加速度计的误差可分为确定性误差和随机误差。确定性误差可通过多位置转位得到精确测量与补偿,而随机误差便成了影响寻北精度的重要因素。为此,人们采用了多种方法对该随机误差进行了建模和滤波。在陀螺随机误差建模方面:文献[1]~[7]等采用自回归滑动平均模型(ARMA(n, m))分别建立了光纤陀螺(FOG)和激光陀螺(RLG)的随机误差模型,并根据该误差模型建立了Kalman滤波器、扩展Kalman滤波器、无迹Ukalman滤波器和自适应Kalman滤波器等,对FOG和RLG误差进行了滤波;文献[8]等采用小波变换对FOG随机误差进行了建模与滤波;文献[9][10]等采用神经网络对FOG随机误差进行了建模。文献[8]采用Allan方差分析法及其改进方法对建模和滤波前后数据的各种噪声源进行了分析,证明了上述方法的有效性。在石英挠性加速度计误差建模方面;文献[11]~[13]采用自回归滑动平均模型(ARMA(n, m))建立了加速度计随机误差模型,并采用Kalman滤波器对加速度计随机误差进行了滤波;文献[14]采用神经网络对加速度计随机误差进行了建模。本文以采用两个FOG和两个加速度计的两位置寻北仪为例,在上述文献建模和滤波的基础上,采用改进型二阶自回归模型-AR(2)模型,在线同时建立了4个惯性传感器的随机误差模型,设计了4个惯性传感器测量信号的12阶Kalman滤波器,开展了陀螺寻北仪中测量信号的在线建模与滤波研究,提高了陀螺寻北仪的寻北精度。
1 FOG和加速度计的静态输出信号的在线建模与滤波
ARMA(n, m)模型要求信号必须为平稳、正态分布和零均值时间序列。理论推导和实验证明[1-7,11-13],FOG和加速度计的静态输出数据基本上可以看作平稳、正态时间序列。但是,由于地速和FOG零偏以及重力加速度和加速度计零偏的存在,FOG和加速度计的静态输出数据不满足零均值的条件。为了可以实现FOG和加速度计的静态输出信号的在线建模及其随机误差的实时滤波,本文采用了改进型ARMA(n, m)模型;由文献[1]~[7]得,AR(2)模型可以作为FOG随机误差的最佳模型。由文献[11]~[13]得,AR(2)模型不是加速度计随机误差的最佳模型,但考虑到AR(2)的模型误差比较小,FOG和加速度计模型误差的一致性以及陀螺寻北仪的卡尔曼滤波器的阶数和计算量,本文将FOG和加速度计的随机误差模型统一选为改进型二阶自回归模型-AR(2)模型,其在线建型和实时滤波过程如下:
设平稳、正态和零均值时间序列为 x1、x2、x3、…xk-2、xk-1、xk、…,则AR(2)模型可以表示为

式中:φ1和φ2为待估计的模型参数;αk为零均值、方差为σ的白噪声,即αk~ (0,σ)。
设 FOG和加速度计的静态输出数据为y1、y2、y3、…yk-2、yk-1、yk、…。该序列可以看作平稳、正态的时间序列,只有进行零均值处理后,才能应用式(1)建模。由于FOG和加速度计的静态输出数据理想值都是常数,因此可以设其平均值为y,则平稳、正态、零均值时间序列可以表示为

将式(2)代入式(1)得:
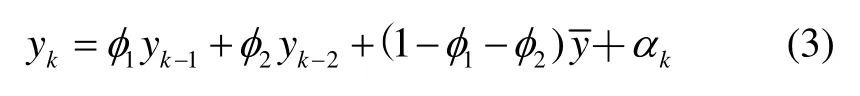
由于 FOG和加速度计的静态输出数据的平均值y可以看作常数,待估计模型参数φ1和φ2也是固定数,因此可以设如下常数:
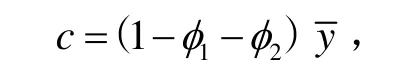
则方程(3)变为

式(4)就是FOG和加速度计的静态输出数据的改进型二阶自回归模型-AR(2)模型。根据FOG和加速度计的静态输出数据的时间序列,由最小二乘法,可以实时估计模型参数φ1和φ2以及常数c,从而在线确定该模型,以便在陀螺寻北仪中对FOG和加速度计的静态输出数据的随机误差进行滤波。
2 光纤陀螺寻北仪的Kalman滤波器
光纤陀螺寻北仪主要包括两个 FOG和两个加速度计,采用两位置寻北方案。因此,可以采集得到 4组数据,需要建立4个改进型二阶自回归模型-AR(2)模型。根据式(4)可得:

其中,g1、g2、a1和a2分别代表FOG1、FOG2、加速度计1和加速度计2。
将常数 cg1、cg2、ca1和ca2也当作状态变量,系统状态方程可以表示为

式中:状态变量

过程噪声


Wk、Vk的统计特性满足以下条件:均值E(Wk)=E(Vk)=0;自相关函数为φWW=Qδkj,φVV=Rδkj;互相关函数φVW(k,j)=0。
对于系统状态方程(5)和量测方程(6),其离散卡尔曼滤波方程为

状态变量初始值X(0)选为测量值初值;系统量测噪声方差R取为FOG和加速度计的零偏稳定性的平方;

3 仿真与试验结果
以我们自行研制的光纤陀螺寻北仪为例,陀螺为北京航空航天大学生产的高精度FOG,加速度计为石英挠性加速度计;FOGx和加速度计x采集的数据如图1和2所示;采用第1节中的改进型AR(2)模型,根据前30 s的数据,分别对两个FOG与两个加速度计的静态测量信号进行在线建模;采用第2节中的12阶Kalman滤波器,对两个FOG与两个加速度计的静态测量信号进行实时滤波;滤波后,FOGx和加速度计x的输出数据如图3和图4所示;采用Allan方差分析法,计算 FOG数据在滤波前后的误差系数,如表 1所示;分别利用建模与滤波前后的数据进行两位置寻北,试验结果如表2所示。由此可得结论:
1)由图1、图2、图3和图4可以看出,建模、滤波前后,FOG和加速度计输出信号曲线的变化规律没有改变,但是建模滤波后的信号噪声明显减小;
2)由表1可以看出,根据Allan方差分析法得到的 FOG建模滤波前后数据的五项误差系数的变化情况:FOG输出数据经过上述建模与滤波后,随机游走、偏差不稳定性、变化率随机游走、变化率斜坡和量化噪声五项噪声源误差系数都小于滤波前的1/2,如FOG的零偏稳定性由原来的0.0196 (°/h)减小为0.0091 (°/h)。由此可得,上述在线模型和滤波有效减小了FOG测量信号的随机误差,提高了其精度。

图1 FOGx静态输出曲线Fig.1 Curves of FOGx data in static state
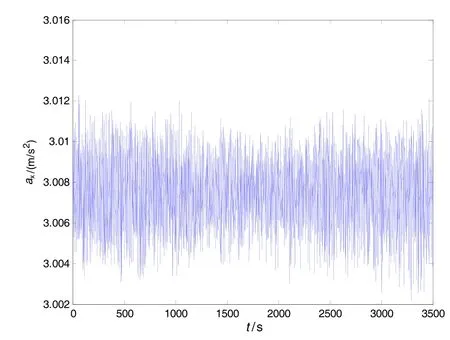
图2 加速度计x静态输出曲线Fig.2 Curves of accelerometer-x data in static state
3)由表2可得,建模与滤波后,寻北误差显著减小,由1.8405 mil减小为1.5160 mil,从而证明了第1节中的AR(2)模型及其在线建模以及第2节中的12阶Kalman滤波器的可行性与有效性。
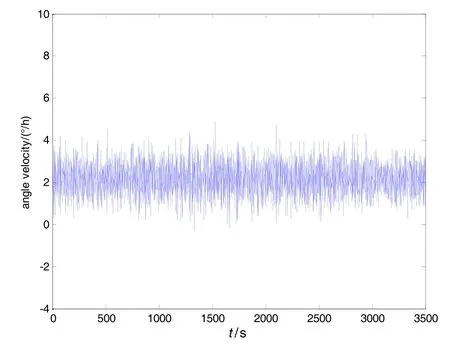
图3 FOGx静态输出经滤波后的曲线Fig.3 Curve of FOGx’s static data after filtering

图4 加速度计x静态输出经滤波后的曲线Fig.4 Curve of accelerometer static data after filtering
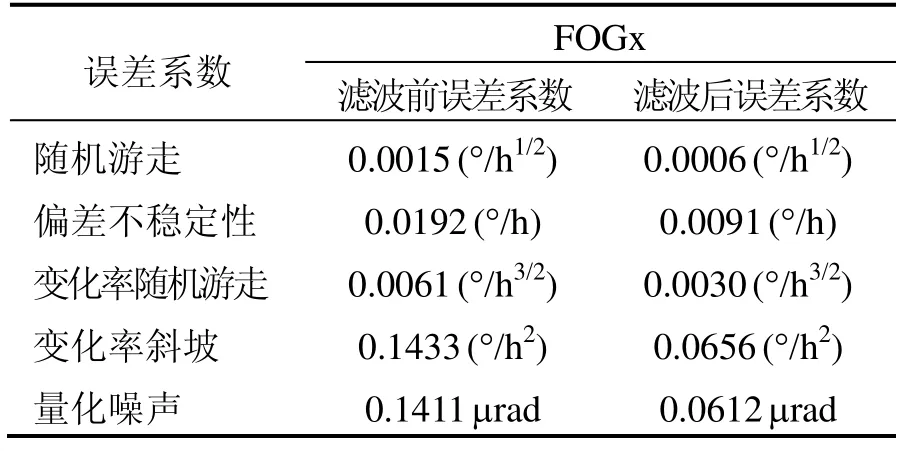
表1 FOGx输出数据滤波前后的误差系数比较Tab.1 Comparison on noise source’s error coefficients
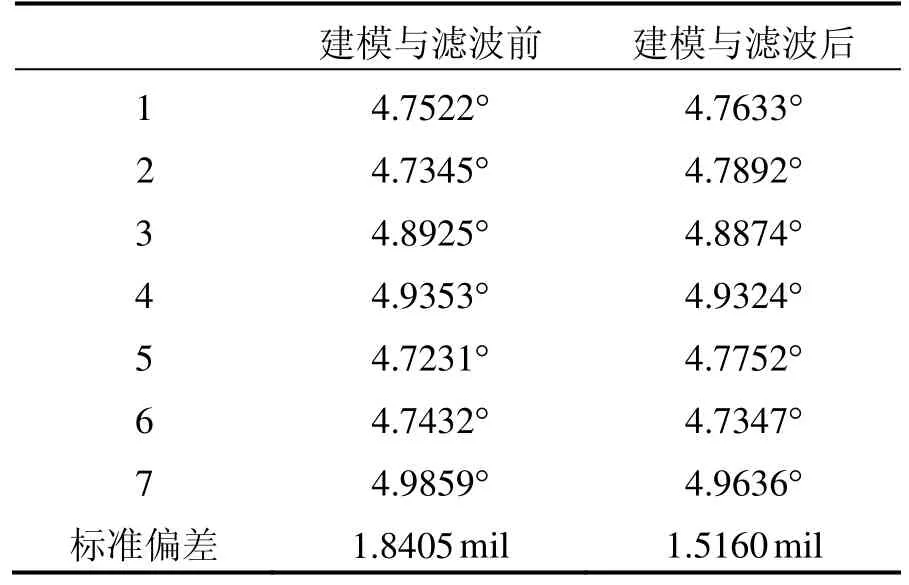
表2 FOG寻北仪在线建模与实时滤波前后的寻北结果比较Tab.2 North-seeking results before and after modeling and filtering the north-seeker in real time
4 结 论
经过对多个FOG和加速度计进行上述建模、滤波以及重复性寻北实验,都得到了相同的结论,即采用本文中的改进型二阶自回归AR(2)模型,可以直接利用FOG和加速度计输出的静态数据,在线建立FOG和加速度计输出信号模型;根据该模型,采用卡尔曼滤波器可以对FOG和加速度计的随机误差实时滤波,可有效减小FOG和加速度计随机误差,提高FOG和加速度计精度;采用AR(2)模型在线建模,建立FOG寻北仪的12阶Kalman滤波器,在减小两个FOG和两个加速度计随机误差的同时,可以提高FOG寻北仪的寻北精度。仿真与试验结果证明了上述建模和滤波方法的可行性与有效性。
(References):
[1] 王立冬, 张春熹. 高精度光纤陀螺信号的在线建模与滤波[J]. 光学工程, 2007, 34(1): 1-5. Wang Li-dong, Zhang Chun-xi. On-line modeling and filter of high-precise FOG signal[J]. Opto-Electronic Engineering, 2007, 34(1): 1-5.
[2] Liu Jie-yu, Shen Qiang, Qin Wei-wei. A signal processing technique for compensating random drift of MEMS gyros [C]//IEEE Guidance, Navigation and Control Conference. Beijing, 2014: 1230-1234.
[3] Narasimhappa N, Sabat S L, Nayak J. Adaptive sampling strong tracking scaled unscented Kalman filter for denoising the filter gyroscope drift signal[J]. Science, Measurement and Technology, 2015, 9(3): 241-249.
[4] Narasimhappa M, Sabat S L, Nayak J. Fiber-optic gyroscope signal denoising using adaptive robust Kalman filter[J]. IEEE Sensors Journal, 2016, 16(10): 3711-3718.
[5] 李杨, 胡柏青, 覃方君, 等. 光纤陀螺信号的解耦自适应Kalman滤波降噪方法[J]. 中国惯性技术学报, 2014, 22(2): 260-265. Li Yang, Hu Bai-qing, Qin Fang-jun, et al. De-noising method of decoupling adaptive Kalman filter for FOG signal[J]. Journal of Chinese Inertial Technology, 2014, 22(2): 260-265.
[6] Tian Yun-peng, Yang Xiao-jun, Guo Yun-zeng, et al. Filtering and analysis on the random drift of FOG[C]// Applied Optics and Photonics: Optical Fiber Sensors and Applications. Beijing, China: 2015: 96760J.1-96760J.6.
[7] Lzmailov E A, Kykhtievitch S E, Tikhomirov V V, et al. Analysis of laser gyro drift components[J]. Gyroscope and Navigation, 2016, 7(1): 24-28.
[8] Wei Wei, Hao Ma. ARMA model and wavelet-based ARMA model application[C]//2nd International Conference on Frontiers of Manufacturing and Design Science. Germany, 2012: 1799-1803.
[9] Mirikitani D T, Nikolaev N. Recursive Bayesian recurrent neural networks for time-series modeling[J]. IEEE Transactions on Neural Networks, 2010, 21(2): 262-274.
[10] Wang Wen-peng, Zhao Bo, Liu Xiao-jun. Application of noise reduction method based on curvelet thresholding neural network for polar ice radar data processing[J]. Journal of Electronics, 2013, 30(4): 377-383.
[11] 王洪, 李磊民, 黄玉清. 石英挠性加速度计零偏分析与建模方法[J]. 自动化仪表, 2014, 35(11): 13-18. Wang Hong, Li Lei-min, Huang Yu-qing. Analyzing and modeling method for the zero offset of quartz flexible accelerometer[J]. Process Automation Instrumentation, 2014, 35(11): 13-18.
[12] 王可东, 熊少锋. ARMA 建模及其在Kalman滤波中的应用[J]. 宇航学报, 2012, 33(8): 1048-1054. Wang Ke-dong, Xiong Shao-feng. An ARMA modeling method and its application in Kalman filtering[J]. Journal of Astronautics, 2012, 33(8): 1048-1054.
[13] Zhong Xin, Zhao Chi-hang, He Jie. Study on four parameters estimation's methods of time-series model in modeling the signal of a quartz flex accelerometer[C]//4thInternational Conference on Measuring Technology and Mechatronics Automation. Germany. 2012: 329-332.
[14] 岳新征, 李磊民, 孙飞. 基于 NAR动态神经网络的石英挠性加速度表参数建模与预测[J].西南科技大学学报, 2016, 31(1): 88-94. Yue Xin-zheng, Li Lei-min, Sun Fei. Quartz flexible acelerometer-based parametric modeling and forecasting NAR dynamic neural network[J]. Journal of Southwest University of Science and Technology, 2016, 31(1): 88-94.
On-line modeling and filtering of measured signals in FOG north-seeker
WANG Li-dong1, WANG Pin2, LUO Xian-quan1, LIANG Guan-hui1
(1. Ordnance Engineering College, Shijiazhuang 050003, China; 2. Wuhan Mechanical Technology College, Wuhan 430075, China)
Aiming at the random errors of FOG and accelerometer in the FOG north-seeker, an improved AR(2) model is designed, and by which the random error models of FOG and accelerometer are built in real time. Based on the models, a 12-order Kalman filter is set up, and the random errors of two FOGs and two accelerometers are filtered in the FOG north-seeker’s north-seeking process. The results of simulations, Allan variance analysis and north-seeking experiments show that these error coefficients, including the random walk, the bias instability, the change rate’s random walk, the change rate’s ramp and the quantification noise in the output signals of FOG, are about one-half as less as those when the random errors of FOGs and accelerometers are not filtered. In addition, the random errors of FOGs and accelerometers are reduced and their precisions are effectively improved by this modeling and filtering method, and the north-seeking error of the FOG north-seeker is reduced by 0.3 mil.
FOG north-seeker; accelerometer; AR(2) model; Kalman filter
U666.1
:A
2016-07-27;
:2016-11-04
国家自然科学基金项目(60671045)
王立冬(1965—),男,副教授,研究方向为光纤惯导技术。E-mail: wlddoctor@163.com
1005-6734(2016)06-0706-04
10.13695/j.cnki.12-1222/o3.2016.06.002
