基于重构伪地球坐标系的捷联惯导初始对准算法

刘 猛，高延滨，李光春，赵 丹

（1. 哈尔滨工程大学 自动化学院，哈尔滨 150001；2. 许继集团有限公司，河南 许昌 461000）

基于重构伪地球坐标系的捷联惯导初始对准算法

刘 猛1，高延滨1，李光春1，赵 丹2

（1. 哈尔滨工程大学 自动化学院，哈尔滨 150001；2. 许继集团有限公司，河南 许昌 461000）

针对捷联惯性导航系统的方位误差对系统误差特别敏感，容易引起闭环卡尔曼滤波初始对准的发散，提出了一种基于重构伪地球坐标系惯导机械编排的初始对准算法。重构伪地球坐标系惯导编排方案在初始位置实现了线性运动误差和方位误差之间解耦，从而消除了导航坐标系旋转角速度误差对方位对准的影响。因此该算法可以减小由系统误差引起的方位对准估计振荡，从而降低了对准系统发散的可能性，进而提高对准系统的稳定性，并改善了捷联惯导初始对准的性能。另外，它不仅适用于常规纬度初始对准，也可以解决极区静态对准问题。最后，常规纬度和极区静态对准仿真证明了该算法具有优良性能。

初始对准；伪地球坐标系；解耦；极区静态对准；捷联惯性导航

捷联惯性导航（SINS）因其独特的优点被广泛用于定位、定向和导航。然而在进入导航之前，精确的初始对准必须要完成[1]，其结果的好坏将直接影响导航的精度，因此初始对准对 SINS是极其重要的。另外随着北极航道的开辟，极区导航变得越来越重要。但是由于极区特殊的地理、电磁条件，使得各种导航手段无法正常工作。惯性导航（INS）因其自主性、隐蔽性和信息的完备性使其成为极区导航的首选[2]。

对于极区惯性导航，游移方位机械编排、格网坐标机械编排和横向地球坐标机械编排已经被提出用于解决极区惯性导航问题。但是惯导的极区初始对准仍然是一个挑战[3-5]。因此极区对准也是极区惯性导航亟待解决的一个重要的问题。

对于捷联惯导初始对准，其通常分为粗对准和精对准两个阶段[6]。在进行对准时，闭环卡尔曼滤波是精对准阶段常用方法之一。然而由于方位对准的不完全可观测以及线性运动误差和方位误差之间耦合，卡尔曼滤波的方位对准对系统误差特别敏感，容易引起闭环系统的发散[7-8]。特别是在较差的粗对准情况下，系统的线性运动误差对 SINS方位对准的影响将是更严重的。另外，由于 SINS东向线性运动的误差对方位误差的影响是随着纬度成正切函数增加的，因此在极区一个很小东向线性运动误差就可能引起非常大方位误差波动，从而造成对准系统的发散。这也是极区对准的一个难点。

为了改善闭环卡尔曼滤波初始对准的性能，常用的方法有变增益卡尔曼滤波、设置较大的初始噪声矩阵及提高粗对准精度方法等[9-11]。对于变增益卡尔曼滤波，其增益是很难预测和控制的，而设置较大的量测噪声矩阵以牺牲对准时间和对准精度为代价来保证系统稳定，另外精确的粗对准在极区也是非常困难得到的。并且我们也可以注意到，所有的这些方法皆是从外部因素考虑解决卡尔曼滤波对准的稳定性，例如从粗对准精度、过程噪声矩阵和量测噪声矩阵等因素。

针对上述问题，本文提出了一种基于重构伪地球坐标系惯导编排的初始对准算法。该算法是从固有惯性导航误差模型（内部固有因素）出发解决捷联惯导卡尔曼滤波初始对准问题。最后通过常规纬度和极区静态对准仿真对该算法进行验证。

1 伪地球坐标系的定义

假设载体的初始经纬度为 λ0和 φ0，则伪地球坐标系Oxpypzp可以通过原地球坐标系Oxeyeze两次旋转得到的。如图1所示，在伪地球坐标系中，其坐标原点仍在地球中心，Np是伪北极点，Oxp轴与原Oze重合，Oyp轴是指向载体初始位置在赤道平面的投影点，Ozp在赤道平面内垂直于Oyp轴。其具体的旋转过程为

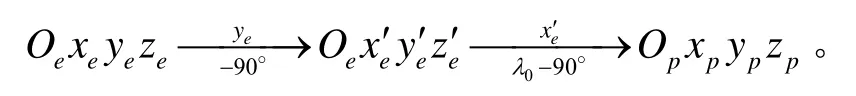
由以上可知，地球坐标系和伪地球坐标系之间的变换关系为

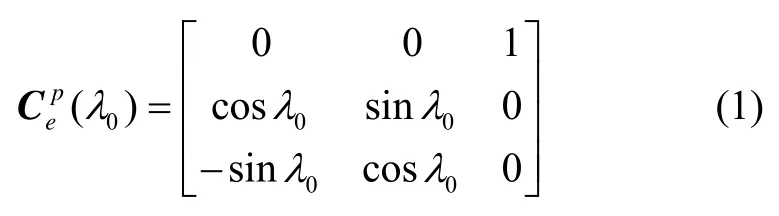
在伪地球坐标系中，载体位置的伪经纬坐标用 λp和φp来表示。根据伪地球坐标系的定义，如图1所示，伪赤道同载体初始位置所在的子午线圈是重合的，则载体的初始伪经纬度为

伪地理坐标系的定义也是同正常地理坐标系相似的。如图1所示，Oxtpytpztp为伪东-北-天坐标系，其坐标原点在载体的重心，Oxtp与Oytp、Oztp遵从右手定则，Oytp指向伪北向，Oztp沿垂直方向指向天向。则伪地理坐标系和地理坐标系Oxtytzt之间有如下的变换关系：

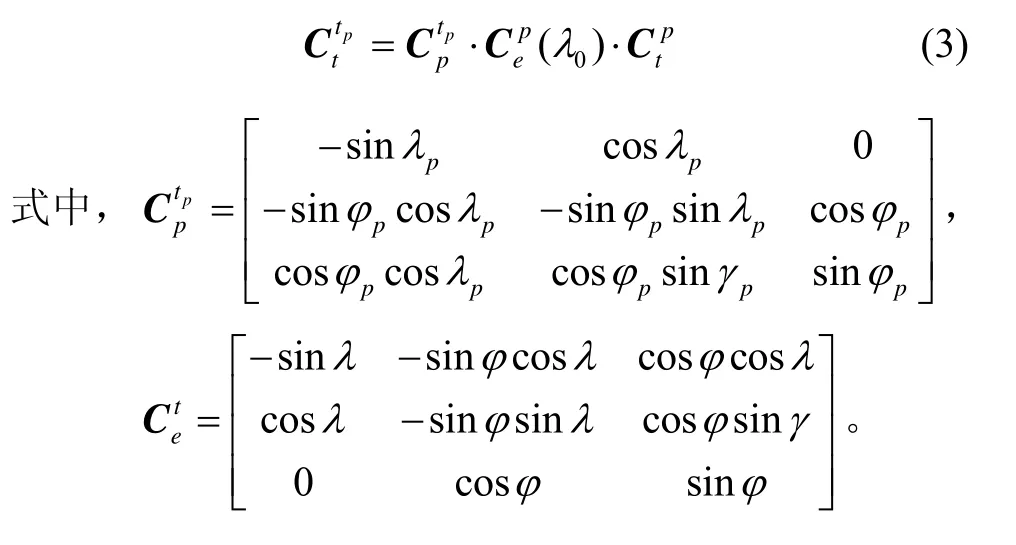
将式(1)(2)代入式(3)可以得到，在初始位置伪地理坐标系和地理坐标系之间的关系为

由公式(4)可知，在初始位置，伪地理坐标系(伪东-北-天)和传统的南-东-天地理坐标系是重合的。因此如果在伪地理坐标系进行机械编排来完成静态初始对准，它将是容易实现的，且不会增加任何附加的困难。

2 伪地球坐标系捷联惯导的机械编排

基于伪地球坐标系惯性导航机械编排与原地球坐标系指北方位系统是相似的。在伪地球坐标系中，捷联惯性导航系统则采用伪指北方位系统进行编排，伪地理坐标系被选为导航坐标系，故数学平台的指令角速度也将发生改变。根据伪地理坐标系的定义可知，仅因地球自转而引起伪地理坐标系的旋转角速度和传统指北方位编排是不一致的，并且可以表示为

式中，Ω表示地球自转角速度。

根据上文的分析，伪地球坐标系下的捷联惯导机械编排可以表示为如图2所示，且捷联惯导系统的姿态、速度和位置更新微分方程为

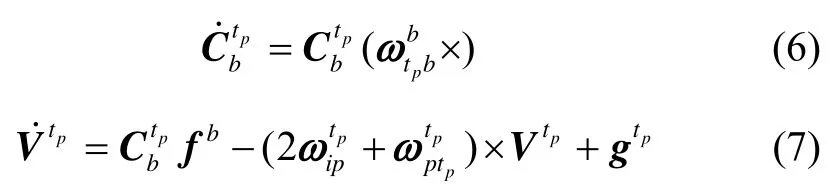
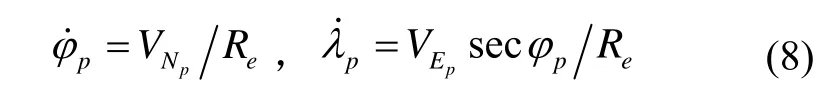
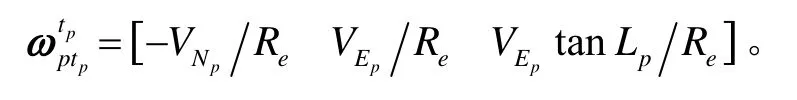
图2 伪地球坐标系捷联惯导系统机械编排Fig.2 Mechanization of strapdown inertial navigation system under pseudo-Earth frame

3 伪地球坐标系捷联惯导静态误差方程

根据伪地球坐标系下捷联惯导机械编排，系统的静态误差方程将是容易得到的，则在小失准角的情况下，伪指北方位系统的静态误差方程为

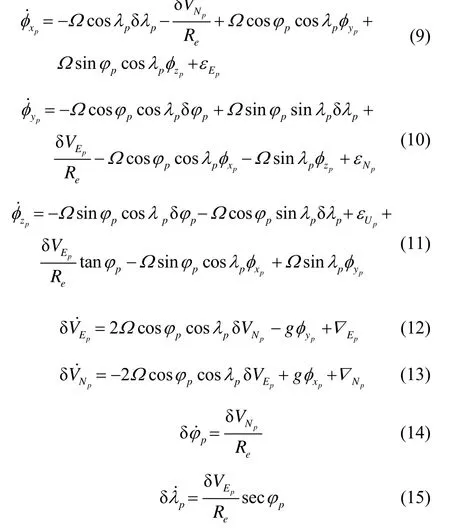
式中：δVEp、δ VNp分别为伪东向和伪北向速度误差；φxp、φyp、φzp为伪地球坐标系中的平台姿态误差；δλp、δφp为伪经纬度误差；∇Ep、∇Np和εEp、εNp、εUp分别为加速度计的零偏和陀螺的漂移在伪地理坐标系中的投影。

4 伪地球坐标系下的静态卡尔曼滤波模型

静基座时，陀螺的漂移和零偏通常被认为是由常值误差和白噪声构成，即∇˙=0，ε˙=0。忽略位置误差和天向速度误差，伪地球坐标系下捷联惯导静基座初始对准的状态方程为

式中：X=[δVEpδVNpφxpφypφzp∇Ep∇NpεEpεNpεUp]T；F(t)为系统状态转移矩阵；W(t)为系统过程噪声，为N(0,Q)的高斯白噪声。

由公式(2)可知，在初始位置，伪纬度总为零，即φp0=0°。因此根据式(9) ～ (15)，伪地球坐标系惯导编排的静态初始对准的状态转移矩阵为

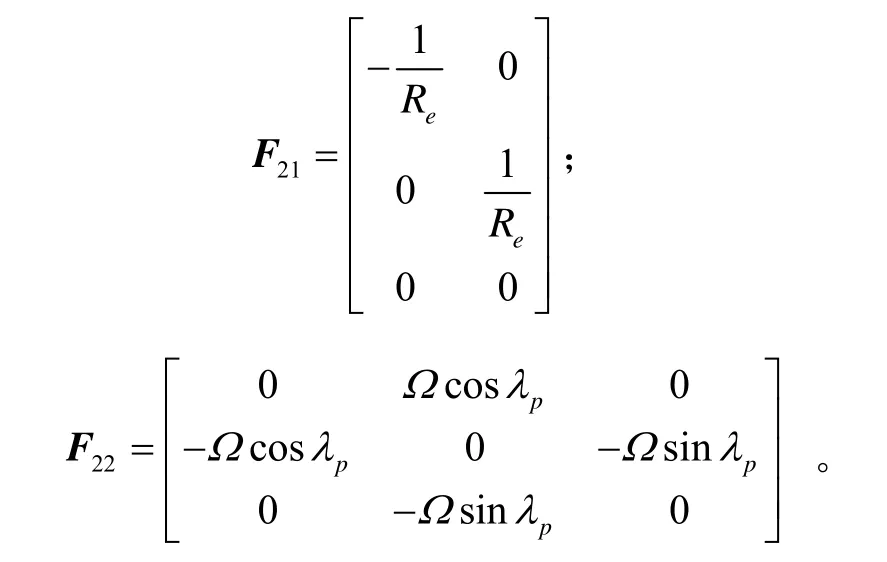
分析伪地球坐标系捷联惯导初始对准的状态转移矩阵，容易发现矩阵F21第三行的所有元素都为零。这意味着线性运动误差和方位误差之间实现了解耦，因此在伪地球坐标系进行初始对准，可以消除了导航坐标系旋转角速度误差（即δω或在传统编排下为δω）对方位对准的影响。另外，由于伪地球坐标系是根据载体初始位置重构的，因此它不受载体初始位置的影响，也可用于极区静态初始对准。

在初始对准过程中，由于失准角的存在，系统将会产生线性运动误差，从而引起导航坐标系旋转角速度误差。另外，由于方位对准是不完全可观测的，因此在传统指北方位编排下，导航坐标系旋转角速度误差将会引较大的方位对准估计振荡，从而可能会造成闭环对准系统的发散，以至于对准失败。特别当粗对准精度较低的情况下，在卡尔曼滤波对准的开始阶段，它的影响将是更加严重的。而本文所建议的伪地球坐标系惯导机械编排在初始位置实现了线性运动误差和方位误差之间解耦，消除了导航坐标系旋转角速度误差对方位对准的影响，因此该算法将具有优良的初始对准性能。此外，由于在传统指北方位编排下，导航坐标系旋转角速度误差对方位误差的影响是随纬度成正切函数增加的，所以在极地地区，其对于闭环系统的影响将是更严重的。因此线性运动误差和方位误差之间解耦对极区初始对准将是非常有利的。由于其不受载体初始位置的影响，故它不仅可以用于常规纬度静态初始对准，同样也可以用于极地地区的静态初始对准，从而解决极区静态初始对准问题。

综上所述，在伪地球坐标下进行初始对准是从惯导系统建模方面消除了导航坐标系旋转角速度误差对方位对准的影响，从而减小了系统误差引起估计震荡，进而提高系统方位对准的稳定性。该算法有望辅助其它从外部因素考虑解决卡尔曼滤波对准稳定性的方法，进一步改善初始对准性能。

对于卡尔曼滤波模型的量测方程，选取两个水平伪速度误差δVEp、δVNp为观测量，则系统的量测方程为

式中：H=[I2×202×8]；V(t)为系统观测噪声，为N(0,R)的高斯白噪声。

为了验证基于伪地球坐标系惯导机械编排的初始对准算法的优越性能，本节分别用常规纬度和极区静态闭环卡尔曼滤波初始对准仿真对其进行验证。

5.1 常规纬度静态初始对准仿真

仿真参数设置如下：初始位置φ0=45°，λ0=126°；载体的真实姿态角θ=γ=ψ=0°；陀螺常值漂移为0.01 (°)/h，随机游走系数为0.001 (°)/h；加速度计常值零偏为1×10-4g，随机游走系数为1×10-5g；采样频率为100 Hz；卡尔曼滤波步长为0.1 s。

设捷联惯导系统粗对准失准角为φx=φy=0.2°，φz=0.5°，分别用正常地理坐标系和伪地理坐标系下两种机械编排进行仿真，其仿真结果如图3所示。在图3中，实线表示使用传统指北方位编排的初始对准结果，虚线表示使用伪地理坐标系机械编排的初始对准结果，图中的绿色线表示协方差矩阵Pk中方位估计误差的两个平方根。由图3可知，在伪地理坐标系下进行初始对准，其估计振荡明显比传统的机械编排小，且收敛时间也要比传统方法短。因此在相同的外部环境下，基于伪地球坐标系惯导机械编排的初始对准可以消除导航坐标系旋转角速度误差对方位对准的影响，从而减小由系统误差引起估计震荡，进而改善静态初始对准性能。

5 仿真与分析

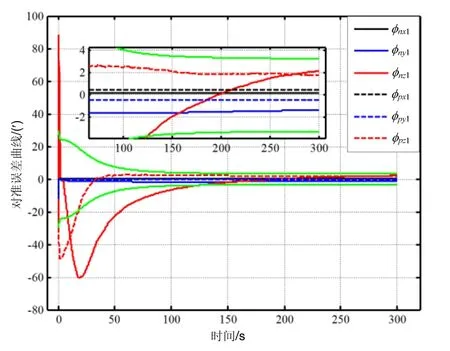
图3 两种机械编排下的静态对准结果对比Fig.3 Comparison on static alignment results under the two mechanizations

然而当粗对准的失准角为φx=φy=0.3°、φz=1°时，仍使用与上文较小粗对准失准角仿真相同的卡尔曼滤波初始噪声参数，则在传统机械编排的卡尔曼估计是发散的。于是采用较大初始噪声矩阵来保持卡尔曼滤波器的稳定，其仿真结果如图4所示。图5为采用与上文较小粗对准失准角仿真相同的卡尔曼滤波初始参数的伪地球坐标系静态初始对准仿真结果。由图4和图5可知，使用这两种算法的方位对准精度和收敛时间分别为3.3′、0.8′和100 s、50 s。因而加大初始噪声矩阵虽然可以保持滤波系统的稳定，但是其收敛速度明显变慢，而且对准精度也是下降的。因此增大初始噪声矩阵的方法是以牺牲对准性能为代价来保持初始对准系统的稳定，故此方法是不可取的。而在较大的粗对准误差下，基于伪地球坐标系惯导机械编排的静态对准性能仍然是较好的。因此基于伪地球坐标系惯导机械编排的静态对准可以减小由系统误差引起估计振荡，从而降低了初始对准系统发散的可能性，并提高系统方位对准的稳定性，进而改善捷联惯导系统的初始对准性能。

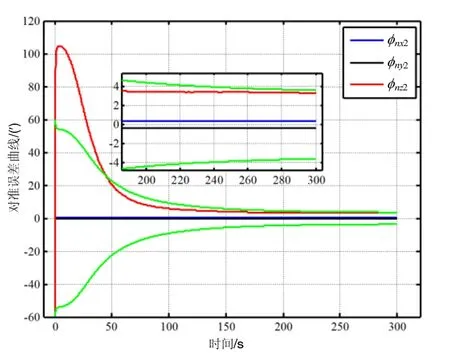
图 4 较大的初始噪声矩阵的静态对准结果Fig.4 Static alignment results using the noise matrix with larger initial value

图5 伪坐标系下静态对准结果Fig.5 Static alignment results under pseudo frame without correction

5.2 极区静态初始对准仿真

为了进一步验证伪地球坐标系下初始对准算法优越性，对极区静态初始对准也进行了仿真。由于随着纬度的升高，地理坐标系的地球自转北向分量越来越小，最终会为零，因此惯性导航静态对准在极点和极点附近将是不能实现的，对极点及极点附近的静态对准研究也将是无意义的，故将极区静态对准仿真的初始位置设为φ0=89°，λ0=126°。另外考虑到惯性导航静态对准系统的方位对准精度不仅与东向陀螺的常值漂移成正比，且与纬度余弦函数成反比，因此随着纬度的升高，静态对准的精度会下降。故在极区静态对准仿真中选用了较高精度的惯性测量单元，其参数设置如下：陀螺零偏为 0.001 (°)/h，随机游走系数为0.0001 (°)/h；加速度计零偏为5×10-5g，随机游走系数为5×10-6g；载体的真实姿态角θ=γ=ψ=0°；采样频率为100 Hz；卡尔曼滤波步长为0.1 s。

由于极地地区高精度的方位粗对准是难以获得的，故设其粗对准失准角为φx=φy=0.5°，φz=3°。图6为采用伪地球坐标系在极地地区89°纬度下的仿真结果。由图6可知，在极地地区，其对准性能仍是比较好的。因此基于重构的伪地球坐标系的初始算法可以用来解决极地静态初始对准问题。

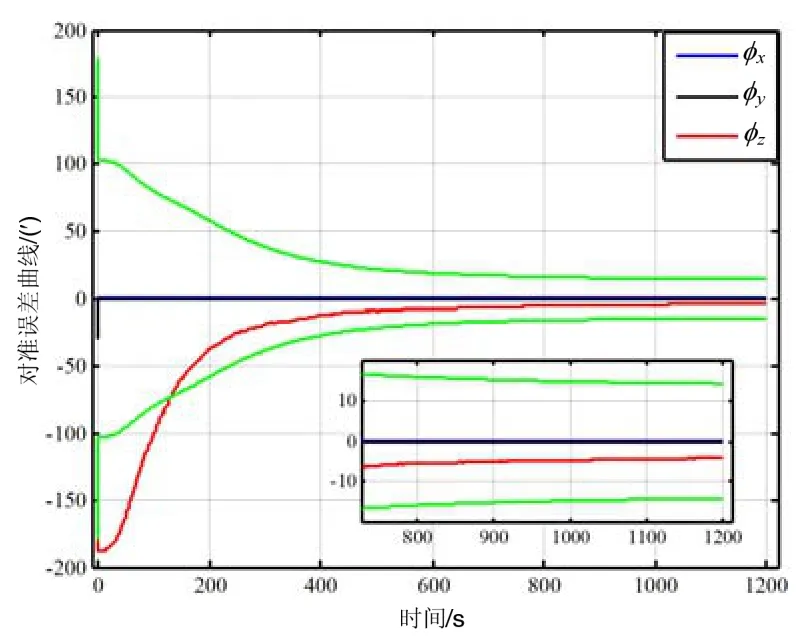
图6 极区静态对准结果Fig.6 Static alignment results in polar region

6 结 论

本文提出了一种基于重构伪地球坐标系的捷联惯导初始对准算法。该算法是从固有惯性导航误差模型（内部固有因素）出发解决捷联惯导卡尔曼滤波初始对准的稳定性问题。与传统机械编排相比，它实现了线性运动误差和方位误差之间解耦，从而消除了导航坐标系旋转角速度误差对方位对准的影响。因此该算法可以减小由系统误差引起估计振荡，从而提高了系统方位对准的稳定性，进而改善了静态卡尔曼滤波初始对准性能。由于伪地球坐标系的重构不受载体初始位置的影响，所以它也可以解决极地静态初始对准问题。常规纬度静态对准和极区静态对准仿真已经验证了此算法的优越性能，结果显示基于重构伪地球坐标系的捷联惯导初始对准算法具有较好的性能。

该算法有望辅助其它从外部因素考虑解决卡尔曼滤波对准稳定性的方法，进一步改善初始对准性能。尽管本文只验证了静态基座初始对准，但是该算法也可以用在准静基座初始对准，并为其它条件下初始对准提供一定的参考价值。

参考文献（References）：

[1] Chang L, Li J, Chen S. Initial alignment by attitude estimation for strapdown inertial navigation systems[J]. IEEE Transactions on Instrumentation & Measurement, 2015, 64(3): 784-794

[2] 朱启举, 秦永元, 周琪. 极区航空导航综述[J]. 测控技术, 2014, 33(10): 5-8. Zhu Qi-ju, Qin Yong-yuan, Zhou Qi. Summary of polar air navigation[J]. Measurement & Control Technology, 2014, 33(10): 5-8.

[3] Salychev O S. Applied inertial navigation: problems and solutions[M]. Russia: BMSTU Press, Moscow, 2004, p14-15.

[4] 周琪, 岳亚洲, 张晓冬,等. 极区飞行间接格网惯性导航算法[J]. 中国惯性技术学报, 2014, 22(1): 18-17. Zhou Qi, Yue Ya-zhou, Zhang Xiao-dong, et al. Indirect grid inertial navigation mechanization for transpolar aircraft[J]. Journal of Chinese Inertial Technology, 2014, 22(1): 18-17.

[5] Li Q, Ben Y, Yu F, et al. System reset of transversal strapdown INS for ship in polar region[J]. Measurement, 2014, 60: 247-257.

[6] Hu J, Cheng X. A new in-motion initial alignment for land-vehicle SINS/OD integrated system[C]//2014 IEEE/ ION Position, Location and Navigation Symposium. 2014: 407-412.

[7] Liu X, Liu X, Song Q, et al. A novel self-alignment method for SINS based on three vectors of gravitational apparent motion in inertial frame[J]. Measurement, 2015, 62: 47-62.

[8] Wu Y, Zhang H, Wu M, et al. Observability of strapdown INS alignment: a global perspective[J]. IEEE Transactions on Aerospace & Electronic Systems, 2011, 48(1): 78-102.

[9] Li Q, Ben Y, Yang J. Coarse alignment for Fiber Optic Gyro SINS with external velocity aid[J]. Optik - International Journal for Light and Electron Optics, 2014, 125(16): 4241-4245.

[10] Lü S, Xie L, Chen J. New techniques for initial alignment of strapdown inertial navigation system[J]. Journal of the Franklin Institute, 2009, 346(10): 1021-1037.

[11] Fang J, Yang S. Study on innovation adaptive EKF for in-flight alignment of airborne POS[J]. IEEE Transactions on Instrumentation & Measurement, 2011, 60(4): 1378-1388.

Initial alignment algorithm for SINS based on reconstructed pseudo-Earth frame

LIU Meng1, GAO Yan-bin1, LI Guang-chun1, ZHAO Dan2
(1. College of Automation, Harbin Engineering University, Harbin 150001, China; 2. XJ Group Corporation, Xuchang 461000, China)

In view that the SINS’s heading error is very sensitive to system errors, which may lead to divergence in the initial alignment by closed-loop Kalman filtering, this paper proposes an initial alignment mechanization based on reconstructed pseudo-Earth frame. The decoupling between the level linear movement error and the heading error is realized at the initial position, eliminating the coordinate rotation angular velocity error’s influence on the azimuth alignment. Therefore the proposed algorithm can decrease the oscillation of azimuth alignment caused by the system errors, and improve the SINS’s alignment stability. In addition, it can also be applied to the static alignment in polar region. Simulations on static alignments in conventional latitude and in polar regions both show that the proposed algorithm has superior performances.

initial alignment; pseudo-Earth frame; decoupling; polar static alignment; strapdown inertial navigation system

U666.1

：A

2016-08-10；

：2016-11-04

中国国家科学技术部国际科技合作项目（2014DFR10010）

刘猛（1988—），男，博士研究生，从事惯性技术研究。E-mail: liumeng_0304@163.com

联 系 人：高延滨（1963—），男，教授，博士生导师。E-mail: gaoyanbin@hrbeu.edu.cn

1005-6734(2016)06-0710-06

10.13695/j.cnki.12-1222/o3.2016.06.003