基于多粒度空间的三支决策方法研究

史进玲

(许昌学院 国际教育学院，河南 许昌 461000)

基于多粒度空间的三支决策方法研究

史进玲

(许昌学院 国际教育学院，河南 许昌 461000)

为弥补传统的二支决策中直接接受或直接拒绝带来的风险，从多个粒度空间，基于信息粒介绍信息表中的三支决策方法.首先讨论了不同的属性集合导出的粒度空间，基于多个粒度空间分析信息粒的构建.其次，从决策粗糙集理论出发，介绍了均方根决策模型，通过多个粒度空间选择一种合适的决策行动.最后，基于贝叶斯最小风险准则，介绍了任意粒度空间中的三支决策方法，为三支决策在人脸识别或智能决策中的应用提出新视角.

决策粗糙集；多粒度；粒空间；三支决策

随着现代信息技术和网络通信的快速发展和应用，大数据[1]已成为信息时代的主要特征.如何有效地处理大数据，对海量的信息具有更强的决策能力和洞察发现力是智能信息处理领域的重要研究内容之一.在传统的信息决策中主要采用接受或拒绝两种策略，但是当信息或获得的证据不足时，接受或拒绝往往对问题的决策带来较大的决策损失.因此，三支决策理论的引入将会避免在决策中直接接受或拒绝带来的风险[2,3]，在三支决策中给出了第三种决策，即选择不承诺选项.目前在医疗诊断、石油勘探、人脸识别等领域得到了广泛的应用[4-7].为有效地将三支决策理论应用于人脸识别或智能决策，本文基于多个粒度空间研究信息表中三支决策方法，为三支决策理论的成功应用提出一种新的研究思路.

1 信息粒与多粒度空间

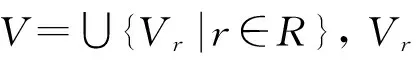
定义2[8]假设S=(U,R,V,f)是一个信息表，令r∈R，v∈V，设rv为信息表上的原子公式，令m(rv)表示U上所有满足f(x,r)=v的个体的集合，称二元对(rv,m(rv))为信息表S上的基本粒.

定义4 设(rv,m(rv))是信息表S=(U,R,V,f)中的基本粒；若φ1和φ2分别由S上有限个原子公式使用合取连接词(∧)得到的合式公式，则称二元对(φ1∧φ2,m(φ1∧φ2))为信息粒，任意的二元对经过有限次合取运算所得到的二元对也是信息粒.

因此，在信息表中任意的信息粒均可由公式φ及其意义集m(φ)构成的，设Gr=(φ,m(φ))表示信息表中的信息粒.

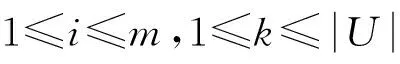
性质1 信息表S=(U,R,V,f)中所有的基本粒构成1阶粒度空间.

由定义5容易证得性质1和性质2，证明略.

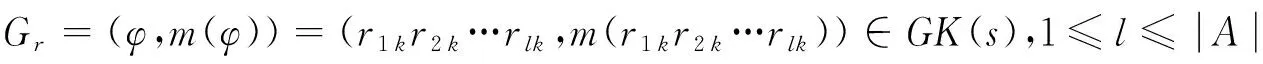
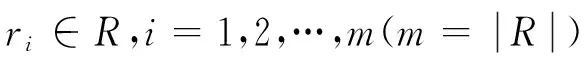
由以上分析可知，知识的粒度随着属性子集的不断增大，即信息粒度的减少，而不断减小，定理1容易证得，证明略.

2 基于多粒度空间的三支决策理论

在粗糙集分析中，传统的决策粗糙集主要基于单粒度范畴，但是在面对复杂的信息系统如不确定的，模糊的或分布式信息系统时，从多个粒度[9-12]挖掘有用的决策支持模式将弥补单粒度决策的不完备性，因此，下面基于多个粒度空间进行粗糙集的三支决策.

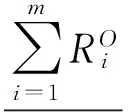
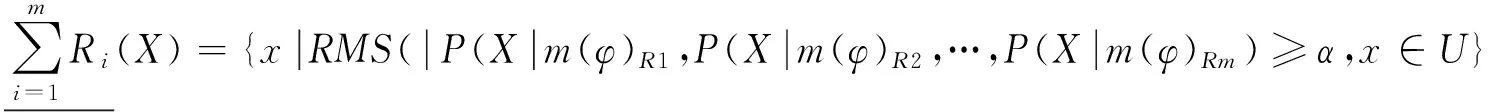
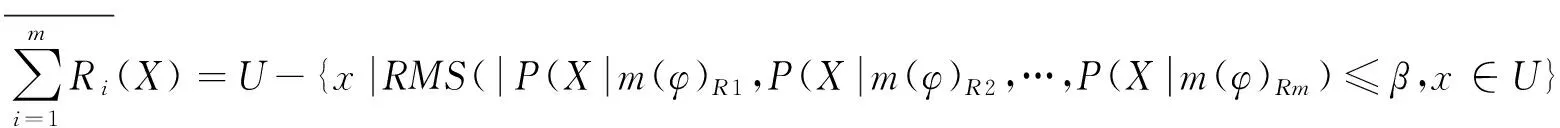
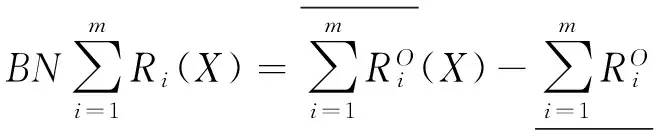
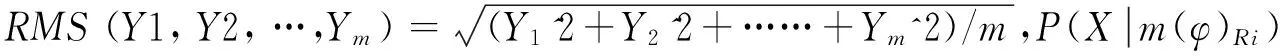
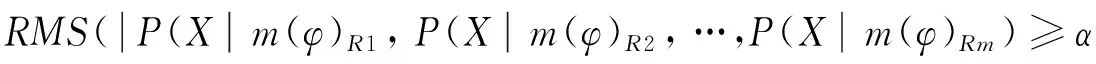
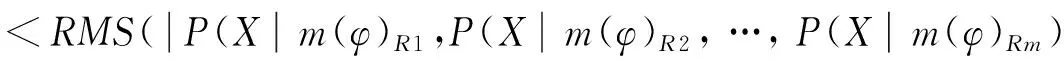
上面的分析主要基于多个粒度综合分析，选择一种最优的决策行动.但是，针对一些信息表可能需要从某个粒度层次出发，分析最小风险决策，因此，下面基于三支决策思想，选择某个粒度层次，从正域决策，负域决策和边界决策中选择一种决策行动并计算其决策风险，使总的损失尽可能小.

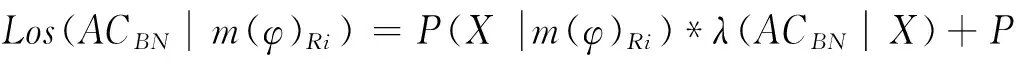
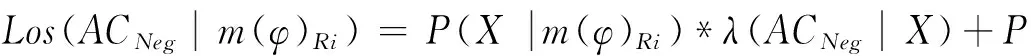
3 基于多粒度的三支决策算法

输入：信息表S=(U,R,V,f)，令集合S=R，T=Φ；

输出：对象x关于决策状态S={X，┐X}的三支决策.

步骤1 若S=Φ，转步骤3；否则，对∀ri∈S，令T=T∪ri，S=S/ri;

步骤2 对∀v∈Vri(x),令Gr=(rik,m(rik));GK(1)=GK(1) ∪Gr，转步骤1；

步骤3 for(l=1;l<=m;l++);

对T中任意l个属性导出公式r1kr2k…rlk，令GK(l)=GK(l) ∪(r1kr2k…rlk,m(r1kr2k…rlk))；

步骤4 从多个粒度空间中深度搜索包含x的对象集m(φ)Ri，计算m(φ)Ri关于X的条件概率之间的均方根；

步骤5 由阈值α、β，计算x关于集合X的粗糙近似，从而得到集合{接受某事件，拒绝某事件，延迟决策} 中的一种决策行动;

步骤6 针对信息表，择优选择一种合适的粒度空间Ri;

步骤7 在属性集合Ri导出的粒度空间中，基于贝叶斯风险决策Ri粒度空间中计算采取这三种行动的条件损失，并采取最小风险决策;

步骤8 比较步骤5和步骤7的决策结果 ，实现最终决策.

4 结语

三支决策理论弥补了传统的二支决策所带来的代价或后果，本文针对信息表分析了不同的粒度空间，从信息粒的构建讨论了不同粒度空间之间的转换，并基于多粒度和贝叶斯最小风险准则介绍了三支决策方法，为三支决策的进一步研究和深入应用奠定了基础.

[1] 徐 计,王国胤,于 洪.基于粒计算的大数据处理[J]. 计算机学报,2015,38(8):1497-1517.

[2] 张里博,李华雄,周献中,等.人脸识别中的多粒度代价敏感三支决策[J].山东大学学报:理学版,2014,49(8):48-57.

[3] 刘 盾,李天瑞,李华雄.粗糙集理论:基于三支决策视角[J].南京大学学报:自然科学版,2013,49(5):574-581.

[4] 刘保相,李 言,孙 杰.三支决策及其相关理论研究综述[J].微型机与应用,2014,33(12):1-3.

[5] 谢 骋,商 琳.基于三支决策粗糙集的视频异常行为检测[J].南京大学学报:自然科学版,2013,49(4):475-482.

[6] 殷 业,柯德营,刘传勇.三支决策理论及应用[J].上海师范大学学报:自然科学版,2015,44(1):95-104.

[7] 刘 盾,姚一豫,李天瑞.三枝决策粗糙集[J].计算机科学,2011,38(1):246-250.

[8] 刘 清,孙 辉,王洪发.粒计算研究现状及基于Rough逻辑语义的粒计算研究[J].计算机学报,2008,31(4):543-555.

[9] 李明星.多粒度粗糙集的理论研究及其应用[D].南京：江苏科技大学,2014.

[10] 桑妍丽,钱宇华.一种悲观多粒度粗糙集中的粒度约简算法[J]. 模式识别与人工智能,2012,25(3):361-366.

[11] Qian Y, Liang J, Yao Y, et al. MGRS: A multi-granulation rough set[J]. Information Sciences, 2010, 180(6):949-970.

[12] Liang J, Wang F, Dang C, et al.An efficient rough feature selection algorithm with a multi-granulation view[J]. International Journal of Approximate Reasoning, 2012, 53(6):912-926.

责任编辑：赵秋宇

Research on Three-way Decision Based on Multi-granularity Space

SHI Jin-ling

(SchoolofInternationalEducation,XuchangUniversity,Xuchang461000,China)

Based on information granule and several granular spaces, we introduced three-way decision in information table to make up the risks of direct acceptance or rejection brought by traditional two-way decision. First, we discussed different granular spaces extracted from different attribute sets and analyzed the construction of information granule in several granular spaces. Second, we choose a proper decision-making in several granular spaces, with decision rough sets theory and root-mean-square decision-making model introduced. Last, based on Bayes minimum risk theory, we introduced three-way decision in arbitrary granular spaces, providing a new perspective for application in human face recognition and intelligent decision-making.

decision rough sets, multi-granularity, granular space, three-way decision

2015-05-10

国家自然科学基金(U1304403)；2016年许昌市科技计划项目

史进玲(1982—)，女，河南社旗人，讲师，硕士，研究方向：粒计算、智能信息处理、生物信息学.

1671-9824(2016)02-0050-03

TP18

A