基于全局动态应力解空间谱单元插值的关键时间点识别

张艳岗　毛虎平　苏铁熊　李　坤　王　军

中北大学,太原,030051



基于全局动态应力解空间谱单元插值的关键时间点识别

张艳岗毛虎平苏铁熊李坤王军

中北大学,太原,030051

摘要：针对结构动态响应优化中动态分析的复杂性与高耗时性问题,提出了基于全局动态应力解空间谱单元插值的关键点识别方法，找到结构动态响应下最危险的时刻。首先利用模态叠加法，获得结构的模态应力分布，并计算全局动态应力解空间，然后利用谱单元离散动态应力绝对极大值点曲线，采用Lagrange插值并调用区域细分全局优化求解器，找到全局动态应力的极大值与极小值，即关键时间点。将该方法应用到124杆平面桁架和均布力与集中力共同作用的结构关键时间点识别问题中，识别结果说明了该方法的可行性和有效性。

关键词：解空间谱单元离散；全局动态应力；Lagrange插值；关键时间点

0引言

工程机械结构几乎都在动态载荷作用下工作，其各种性能均表现为时间的函数。为了使机械结构的动态性能达到极致，确保其在动载环境下可靠工作,目前最行之有效的办法是进行结构动态响应优化设计。然而,在动态响应优化过程中，优化器需要反复调用与设计变量相关的目标函数和约束函数，最直接的方法是通过结构动态分析获得相关数据，然而结构瞬态动力学分析非常复杂和耗时[1-2],因此动态响应优化设计存在很大困难，有时是不太可能实现的。

动态优化设计的参数变化使得应力解空间在整个时间域和结构空间域上变化,即不论是目标函数还是约束函数在随时间变化的同时，其空间位置也在发生变化。与此同时，结构静态优化技术已经趋于成熟，在此背景下将动态优化问题转化为静态优化问题成为了可能。既然要转化，那么首先要解决的问题是在哪个时刻转化，即等效转化为结构在哪个时刻的动态响应，这是动态优化转化等效静态优化的关键一步。文献[3]研究了3种识别关键时间点的方法:第一种方法采用自适应搜索技术，在3点或5点拟合二次函数，然后运用优化方法得到极值点，该方法适合于响应比较缓慢的情况；第二种方法利用最小二乘抛物线样条函数来近似结构的动态响应，该方法可以有效近似噪声动态响应；第三种方法是超峰值法，采用包括设计变量倒数的一阶泰勒展开来近似约束函数。此外,文献[3]中的关键时间点是针对直接求解动态优化问题提出的，仅对与时间相关的约束函数进行了近似，并利用近似函数获得关键时间点。这种方法满足了与时间相关的约束函数，认为时间域上的所有时间点都满足约束，而没有考虑目标函数通常也是与时间相关的函数。在结构动态优化过程中，对目标函数的求解也需要进行动态响应分析，因此没有从根本上解决问题。

文献[4]采用动态位移响应对时间的微分等于零来确定关键时间点，然而微分求解比较困难，并没有详细研究求解方法；而且，即便已经确定关键时间点，即动态位移响应的极值点为关键时间点，虽然从一定意义上可以说明结构在动态载荷作用下位移响应达到极值的时刻最危险，然而位移达到极值的时刻应力不一定也达到极值时刻[5]；再者目前的研究文献中仅仅以结构某一个节点的动态位移绝对值最大为结构关键时间点,没有从结构全局考虑最危险的时刻。因此,将某一节点动态位移响应达到极值的时刻作为结构最危险的时刻来进行结构设计，结构可能欠设计或过设计。

课题组在前期研究中发现,利用谱单元离散插值一个未知函数的精度非常高[6-7],并在系统动力学分析中得到应用验证,可是对于零部件结构的进一步设计需要借助有限元软件来实现。笔者前期在研究动态优化时，提出了基于动态应力解空间谱元离散的关键时间点识别方法[8],旨在找到结构受动态载荷作用最危险时刻，为下一步等效静态转化提供转化时间点;笔者在进一步研究中发现结构最危险的时刻并不是某一个单元的应力达到极值的时刻,而应该是结构全局动态应力达到极值的时刻。全局动态应力是结构在动态载荷的作用下，结构所有单元中的应力最大值,并且最大应力随时间变化，最大应力发生的单元也随着时间变化。因此，本文从结构全局动态应力的角度来确定关键时间点，提出全局动态应力解空间谱单元插值的关键时间点识别方法。

1谱单元插值

对未知函数的插值,学者们一直不断探索新的方法以追求高精度,但往往由于被插值函数的复杂性，插值效果并不理想。研究中发现在正交多项式的零点插值时,能够获得高精度插值函数[9]。

(1)

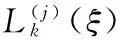
Legendre正交多项式是Sturm-Liouville form方程的解：

[(1-ξ2)P′(ξ)]′+n(n+1)P(ξ)=0

(2)

式中,n为Legendre正交多项式的阶数。

它的权函数ω=1。k阶Legendre多项式可以定义如下：

(3)

由于Legendre多项式的零点不包括区间端点,因此引入Lobbato多项式。Lobbato多项式是通过Legendre多项式的微分定义的,即

(4)

其满足正交特性:

(5)

式中,δi j为Kronecher函数。

GLL点定义如下：

(6)

式(6)的解为GLL点，其中,N为插值次数。

求解式(6)可以获得GLL点坐标值,16次插值GLL点的分布如图1所示。对龙格函数分别进行平均离散插值和GLL点离散插值，可以清楚地看到GLL点离散插值的高精度优势,见图2。

图1　16次插值GLL点分布

图2　平均离散与GLL 点离散插值精度比较

2全局动态应力

承受动态载荷的结构响应都是时间的函数，动态应力也不例外。对于成熟的有限元法来说，结构动态应力不仅是时间的函数还是位置的函数，即结构的每一个空间位置点的动态应力均是时间的函数，变化趋势基本一致，但由于受动态载荷的结构是振动的，结构每一空间位置的动态应力达到极值的时刻不一定相同。本文在前期研究基础上提出更加合理的基于全局动态应力解空间关键时间点识别方法。

结构在动态载荷作用下，其任一点i的动态应力满足[10]:

(7)

全局动态应力对应的关键时间点可以表示为

tCTP(|σ|G)=arg max|σ(i)(t)|

(8)

3关键时间点识别

结构动态优化需要反复进行动态分析，每迭代一次需要n+1次动态分析[11]。因此,基于等效原理将动态载荷转化为静态载荷，利用结构静态优化代替动态优化，可以有效提高动态优化效率。本文提出基于全局动态应力解空间谱单元插值的关键点识别方法，其流程见图3，具体步骤如下：

图3　基于全局动态应力的关键时间点识别流程

(1)建立有限元动力模型。运动微分方程可表达为

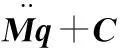
(9)

M=ΦTmΦC=ΦTc Φ

K=ΦTkΦF=ΦTf(t)

(2)动力学分析。采用模态叠加法,先求解式(9)，获得q,然后得到结构的节点位移x=qΦ,再由公式σk(t)=DBkqkΦ获得第k阶模态应力,通过式(7)得到结构动态应力,最后应用式(8)获得结构全局动态应力。

(3)全局动态应力解空间谱单元离散。利用式(2)～式(6)将全局动态应力进行解空间谱单元离散，并计算GLL点对应的结构全局动态应力的值|σ|G(tGLL)。

(4)Lagrange插值结构全局动态应力。Lagrange插值函数为

(10)

其中,Φk+1(ξ)=(ξ-ξ1)(ξ-ξ2)…(ξ-ξk+1)为GLL点对应的全局动态应力插值基函数,GLL点对应的全局动态应力值等于步骤(3)中获得的值；Lk(ξ)为全局动态应力在GLL点上Lagrange插值函数。

(5)识别时间关键点。由于结构动态应力不仅是时间的函数还是位置的函数，即结构的每一个空间位置点的动态应力均是时间的函数，因此全局动态应力解空间函数特性极为复杂，一般为非线性多峰值函数。结合前期优化设计经验，文中采用区域细分算法(DIRECT)计算结构全局动态应力的绝对极大值点。DIRECT算法是一种全局优化算法，该算法既不需要确定目标函数的具体方程，同时也不要求相关的导数信息，而是自动根据优化迭代过程中的每个采样点处的目标函数估值和超矩形的区域细分情况选择搜索方向，因而非常适合于黑盒函数的仿真优化，而且它能够保证收敛到全局最优点。采用的基于全局动态应力关键时间点识别的数学模型如下：

(11)

其中，M为全局动态应力解空间离散的单元数；k为每一个单元离散GLL点数；|σ(i)(tk)|max为第i个单元的第k个GLL点对应的全局动态应力；t0为仿真开始时间,通常为0;t1为仿真结束时间。

4应用验证

4.1124杆平面桁架

(a)124杆平面桁架

(b)动态载荷图4　124杆平面桁架及动态载荷

如图4所示,该平面桁架结构有49个铰链,94个自由度。弹性模量E=207 GPa,泊松比ν=0.3,密度ρ=7850 kg/m3,杆的截面积为64.5 mm2。动态载荷为半正弦函数(图4)。在节点1、20、19、18、17、16、15的x正方向作用同样大的动态载荷,在节点1、2、3、4、5的y负方向也作用同样大的动态载荷。

图5所示为124杆平面桁架全局动态应力谱单元离散插值结果，从图中可以看出结构的全局动态应力非常复杂，是高度非线性多峰值函数。谱单元Lagrange插值全局动态应力精度非常高，应用DIRECT全局优化器准确地找到了关键时间点。

图5　124杆平面桁架全局动态应力

图6　单元15的轴向应力时间历程

图7　节点15的x方向位移时间历程

如果从某一节点的动态位移或者动态应力出发，寻找关键时间点，当然可以找到对应的“关键时间点”,见图6、图7。将不同识别方法得到的关键时间点汇总至表1，可以发现：基于位移识别方法获得的两点为t1=0.096 698 411 s,t2=0.192 408 258 s，t1时刻节点15x方向正位移达到最大,t2时刻节点15x方向负位移达到最大；基于局部应力识别方法获得的两点为t1=0.106 521 572 s,t2=0.192 519 952 s,t1时刻单元15拉应力达到最大,t2时刻单元15压应力达到最大;基于全局动态应力识别方法也获得两点，即t1=0.102 063 859 s，t2=0.192 058 523 s,t1时刻全局某一点拉应力达到最大,t2时刻全局某一点压应力达到最大。位移关键点与局部应力关键点不一致,最大相差0.009 823 161 s,也就是说位移达到最大时,局部应力还没有达到最大，存在一个时间差；而全局应力关键点与局部应力关键点也不一致，最大相差0.004 457 713 s,说明局部应力达到最大时，全局应力还没有达到最大，存在一个时间差。

表1　124杆平面桁架关键时间点识别结果

4.2均布力与集中力作用的平面桁架

图8所示为均匀分布力与集中力共同作用的平面桁架结构。弹性模量E=207 GPa,密度ρ=7850 kg/m3,竖直杆横截面积为0.03 m2,水平杆横截面积为0.0068 m2。半正弦均匀分布力F1(t)作用在水平杆上,半正弦集中力F2(t)作用在节点2和节点3处。

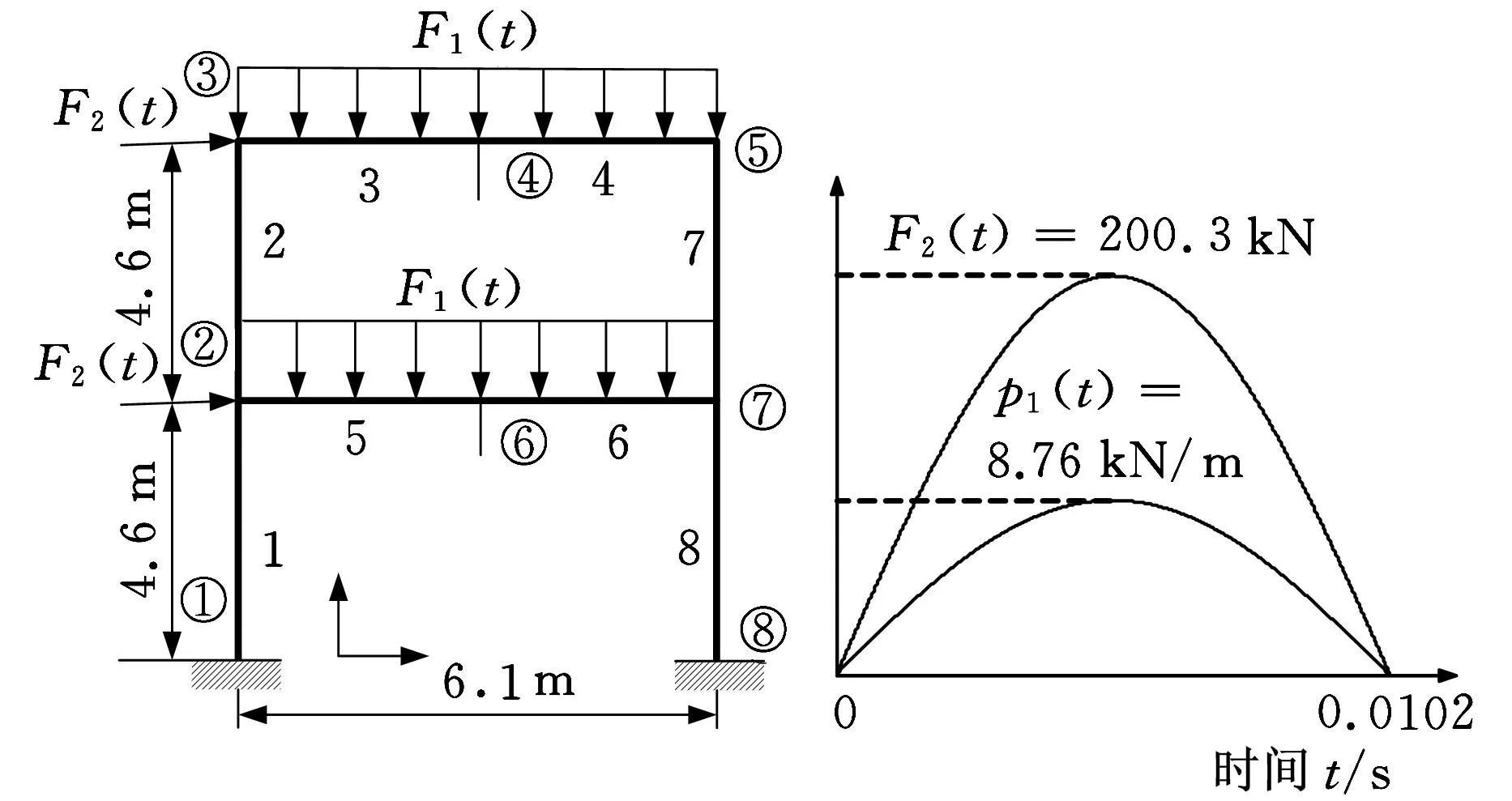
图8　均布力与集中力作用的平面桁架

图9所示为应用本文方法得到的桁架全局动态应力及关键时间点，从图中可以看出全局动态应力不仅呈非线性多峰值状态，而且似乎没有规律可循；可以肯定的是无论全局动态应力解空间多么复杂，谱单元Lagrange插值总是体现其优越性，在此基础上找到关键时间点。

图9　均布力与集中力作用的平面桁架全局动态应力

图10　均布力与集中力作用的平面桁架单元10的动态应力

图11　均布力与集中力作用的平面桁架节点12的位移响应

图10、图11所示分别是从局部动态应力与位移的角度来识别关键时间点的结果。将不同识别方法得到的关键时间点汇总至表2，可以发现3种方法总是有时间差的。另外基于全局动态应力的关键时间点识别方法还可获得结构最大应力值,这为结构动态设计从另一个角度提供参考。当然，如果以位移或局部应力为依据识别关键时间点，其对应时刻不是结构最大应力的时刻，这样可能造成结构欠设计。

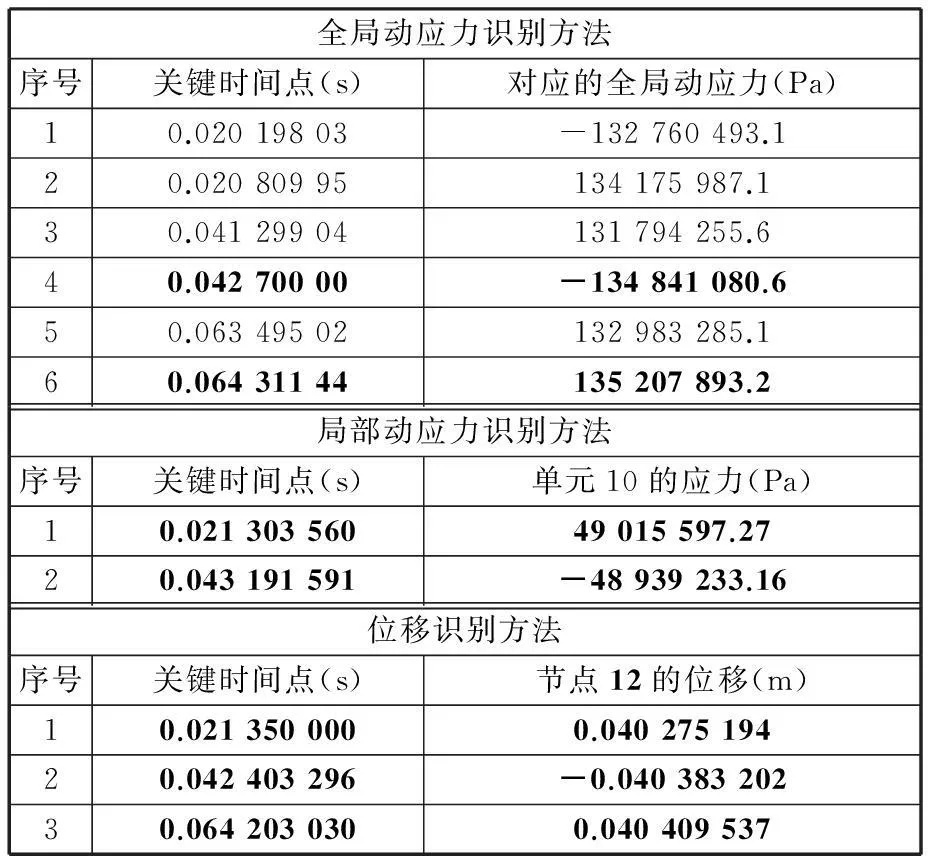
表2　均布力与集中力作用的

5结论

(1)结构动态应力最大的时刻与动态位移最大的时刻存在一个时间差，以动态应力最大时刻为结构关键时间点，虽然相比以位移最大时刻为结构关键时间点合理,然而结构某一点应力达到最大时，全局动态应力并不一定达到最大，因此以全局动态应力最大时刻为结构关键时间点最合理。

(2)应用谱单元离散插值全局动态应力解空间,可获得高精度的插值函数。结构全局动态应力呈现极度非线性多峰值，采用在GLL点处Lagrange插值获得高精度的全局动态响应解空间近似函数。

(3)通过全局优化算法对谱单元离散插值函数进行寻优，获得满意的关键时间点。应用局部优化算法对谱单元离散插值函数寻找最大值点，往往会由于初始点的不同而找到不同的局部最优点，区域细分全局优化算法可以找到全局最大值与全局最小值，对应的就是全局应力最大拉应力与全局应力最大压应力。

参考文献:

[1]James M L.Vibration of Mechanical and Structural Systems[M].2nd ed. New York:Harper Collins,1994.

[2]Clough R W.Dynamics of Structures[M].New York:McGraw-Hill,1993.

[3]Grandhi R V, Haftka R T, Watson L T. Design-oriented Identification of Critical Times in Transient Response [J]. AIAA Journal, 1986, 24(4):649-656.

[4]Choi W S, Park G J. Transformation of Dynamic Loads into Equivalent Static Loads Based on Modal Analysis [J]. Int. J. Numer. Meth. Engng.,1999,46: 29-43.

[5]张艳岗.基于关键时间点的能量等效静态载荷法及结构动态响应优化研究[D].太原：中北大学,2014.

[6]Zhang Yangang, Su Tiexiong. Dynamic Analysis of Diesel Engine Piston Based on Time Spectral Element Method [J]. Applied Mechanics and Materials，2013，415：565-568.

[7]毛虎平，吴义忠，陈立平. 基于时间谱元法的动态响应优化[J]. 机械工程学报，2010，46(16)：79-87.

Mao Huping, Wu Yizhong, Chen Liping. Dynamic Response Optimization Based on Time Spectral Element Method[J].Journal of Mechanical Engineering, 2010，46(16)：79-87.

[8]张艳岗,苏铁熊，毛虎平，等.动态应力解空间谱元离散的关键时间点识别方法[J].机械工程学报,2014,50(3):82-87.

Zhang Yangang,Su Tiexiong,Mao Huping,et al.Critical Time Points Identification Method for Solution Space of Dynamic Stress Based on Spectral Element [J].Journal of Mechanical Engineering,2014,50(3):82-87.

[9]Pozrikidis C.Introduction to Finite and Spectral Element Methods Using Matlab[M].New York:Chapman and Hall/CRC,2005．

[10]张汝清,殷学纲,董明.计算结构动力学 [M].重庆: 重庆大学出版社, 1987.

[11]毛虎平, 吴义忠, 陈立平. 基于多领域仿真的SQP并行优化算法[J]. 中国机械工程, 2009, 20(15): 1823-1829.

Mao Huping,Wu Yizhong,Chen Liping.SQP Parallel Optimization Algorithm Based on Multi-domain Simulation[J].China Mechanical Engineering,2009,20(15):1823-1829.

(编辑袁兴玲)

Critical Time Point Identification for Global Dynamic Stress Based on Spectral Element Interpolation of Solution Space

Zhang YangangMao HupingSu TiexiongLi KunWang Jun

North University of China,Taiyuan,030051

Abstract:According to the complexity and high-cost characteristics of dynamic analyses in the structural dynamic optimization processes,a critical time points identification method for solution space of global dynamic stress based spectral element interpolation was proposed.The most dangerous time points of the structure dynamic response were found.The modal stress distribution was obtained by using the modal superposition method,and then, the solution space domain of the global dynamic stress was computed.The Lagrange interpolation techniques were applied in the solution space domain to get the high precision function of the global dynamic stress. The absolute maximum points, that is, the critical time points,were found by executing the global DIRECT optimizer. Last, two examples of 124-member plane truss and the structure subjected to uniform and concentrated force were used to illustrate the feasibility and validity of the proposed method.

Key words:spectral element discretion of solution space;global dynamic stress;Lagrange interpolation;critical time point

作者简介：张艳岗,男,1981年生。中北大学机械与动力工程学院讲师、博士。研究方向为结构动力学建模与仿真、结构动态响应优化。毛虎平,男,1974年生。中北大学机械与动力工程学院副教授、博士。苏铁熊,男,1963年生。中北大学机电工程学院教授、博士研究生导师。李坤,男,1981年生。中北大学机械与动力工程学院讲师、博士。王军，男, 1979年生。中北大学机械与动力工程学院博士生。

中图分类号：TH122

DOI：10.3969/j.issn.1004-132X.2016.05.021

基金项目：国家自然科学基金资助项目(51275489)

收稿日期：2014-12-10