无耦合完全各向同性1T1R并联机器人机构构型综合

陈　海　曹　毅,2,3　秦友蕾

1.江南大学，无锡，2141222.江苏省食品先进制造装备技术重点实验室，无锡，2141223.上海交通大学机械系统与振动国家重点实验室，上海，200240



无耦合完全各向同性1T1R并联机器人机构构型综合

陈海1曹毅1,2,3秦友蕾1

1.江南大学，无锡，2141222.江苏省食品先进制造装备技术重点实验室，无锡，2141223.上海交通大学机械系统与振动国家重点实验室，上海，200240

摘要：基于螺旋理论对具有无耦合、完全各向同性特点的1T1R并联机构进行了构型综合，综合的并联机构采用支链独立驱动原则，即并联机构的输出运动是由独立的输入驱动提供的。首先根据期望1T1R并联机构的运动特征(沿Z轴的移动和绕Z轴的转动)和完全各向同性并联机构的正逆雅可比矩阵必为对角阵的要求，利用螺旋理论构造满足所期望形式的正逆雅可比矩阵；其次根据正逆雅可比矩阵所要满足的条件，确定支链驱动副作用于动平台上的使动螺旋，再得到该使动螺旋对应支链上的表示驱动副的驱动螺旋和除驱动螺旋之外的其他运动螺旋系，据此可完成支链结构螺旋系的配置；最后根据约束螺旋理论依次取出两条支链连接动平台和定平台得到并联机构。通过这种方法得到大量无耦合完全各向同性1T1R并联机构。最后对综合出的一种并联机构进行了运动学分析，验证了构型方法的正确性。

关键词：螺旋理论; 支链驱动; 并联机构; 型综合

0引言

并联机构相对于串联机构来说，具有一些独特的优点，如承载能力高、刚度相对较强、惯性相对较小等，其中Delta机构的广泛应用更是激发了广大研究人员对并联机构的研究兴趣[1]。并联机构的型综合一直是机构学研究的热点，国内外许多学者在这方面做了大量的工作，主要有基于位移群论的构型方法[2]、基于螺旋理论的构型方法[3]、基于拓扑结构的构型方法[4]三大类，并得到了许多的并联机构构型[5-6]。

最初，综合的并联机构具有6个自由度，但后来发现，在许多应用场合，并不需要这么多的自由度，由此少自由度并联机构逐渐进入人们视野。并联机构结构复杂，控制起来相对较难，而且关于机构的整体性能以及结构刚性等问题也未得到很好的解决。为了克服上述缺点，学者们开始针对一些特殊类型并联机构展开了研究，如解耦并联机构[7-8]、完全各向同性并联机构[9-10]等。Carricato等[11]在2002年证明存在一类特殊的移动并联机构，这类并联机构在整个工作空间内都存在着一个一直不变的正交的正雅可比矩阵和一个对角逆雅可比矩阵，此类机构也属于完全解耦并联机构。Gogu[12]在2004年提出了一种基于线性变换理论的方法来综合完全各向同性移动并联机构；Carricato[13]在2005年根据螺旋理论也提出了一种方法来综合四自由度3T1R完全各向同性并联机构，并且综合出的机构也是解耦的；张彦斌等[14]根据互易螺旋理论综合了2T1R和3T类完全各向同性并联机构。目前在显微操作、精密仪器等领域，机器人末端精度问题仍然没有被有效解决，串联机构存在误差累积大、刚性差等问题，而并联机构从某种程度上可以弥补这一不足。所以对于1T1R无耦合完全各向同性并联机构的构型研究具有一定的意义，这类并联机构具有控制简单、刚性相对较好、精度较高的特点，具有一定的应用前景。

本文基于螺旋理论对无耦合完全各向同性1T1R并联机构进行构型综合。

1理论基础

1.1螺旋理论

文献[15]研究表明，螺旋的组成形式为(S;S0)，S为原部，表示方向矢量，S0为对偶部，且有：

S0=r×S+hS

(1)

其中，r为坐标原点到S上任一点的位置矢量，h为螺旋的节距。螺旋也可用Plüker坐标(LMN；PQR)来表示。

1.2互易螺旋

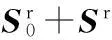
(2)

则螺旋$1和螺旋$2互为反螺旋，其中“∘”表示两螺旋的互易积。

1.3使动螺旋

使动螺旋表示驱动副作用于动平台上的力或力偶，当其形式为$i=(lmn;pqr)时，表示作用力；当其形式为$i=(000 ;lmn)时，则表示一个作用力偶。

1.4约束螺旋

当螺旋表示约束力线矢和约束力偶时，通过求取反螺旋可以得到机构的约束螺旋系，支链约束的共同作用限制了机构的自由度，其具体约束条件和被约束自由度参见文献[15]。

2解耦和完全各向同性并联机构特性分析

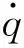
(3)

(4)

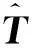
(5)

分支约束螺旋系限制了动平台沿任何不平行于Z轴方向的旋转自由度和垂直于Z轴方向的移动自由度，即任何不平行于Z轴方向的v值和w值恒为零。对应于使动螺旋$ai(i=1, 2)，在式(5)中将使动螺旋的形式改变，这并不改变式(5)的意义，可以得到下式的形式：

(6)

(7)

(8)

如果Jv是可逆矩阵，则有：

(9)

取：

(10)

式中，J为机构的雅可比矩阵。

若期望机构为无耦合完全各向同性并联机构，则当机构雅可比矩阵为对角阵时，满足无耦合并联机构条件。对于完全各向同性并联机构，则有：

J=c2I

(11)

其中，c为常数，I为单位阵。由式(10)可知，当Jr、Jv均为对角阵，且对角线上元素都相等时，则此机构在工作空间内雅可比条件数恒为1，即为完全各向同性机构[11]。所以，只需保证Jr、Jv均为对角阵，则机构具有很好的各向同性，且属于完全解耦并联机构。

3无耦合完全各向同性1T1R并联机构型综合原理

由上述分析可知，如果能保证机构的正逆雅可比矩阵均为非零对角阵，则此机构一定是完全各向同性并联机构，也是完全解耦并联机构。基于此结论，本文提出了一种利用螺旋理论来构造正逆雅可比矩阵均为对角阵的方法，进而得到满足期望要求的并联机构。由于机构的正逆雅可比矩阵与使动螺旋和驱动螺旋有关，所以可以通过给定使动螺旋和驱动螺旋的形式，来得到对角非零的正逆雅可比矩阵。又因为驱动螺旋是根据驱动副得到的，在支链中随着机构动平台及支链的运动，驱动螺旋的表达式可能会发生改变，所以本文中驱动副均和固定平台直接相连，以保证驱动螺旋的形式不会随着支链的运动而改变。

同时由文献[16]可知，对于移动并联机构，其驱动副既可为移动副，也可为转动副，当驱动副为转动副时，该分支同时需具有一个与驱动副构成2R平行子链的转动副，这种情况相当于一个转动副和一个移动副的线性组合，其作用效果和用移动副直接驱动是相同的。结合以上分析，可依据独立驱动原则，利用螺旋理论完成无耦合完全各向同性1T1R并联机构的构型，其原理过程如下：

(1)根据支链独立驱动原则和机构正逆雅可比矩阵需为对角阵的要求，确定支链驱动控制的动平台输出自由度，然后给出该支链驱动副作用于动平台上的使动螺旋形式。

(2)根据使动螺旋确定支链中的驱动螺旋，其中当使动螺旋为力线矢类螺旋时，驱动副可以是移动副或是2R平行子链转动副，对应的驱动螺旋为偶量螺旋或力线矢螺旋；当使动螺旋为偶量类螺旋时，驱动副只能为转动副，对应的驱动螺旋为力线矢螺旋。

(3)根据支链上除驱动螺旋之外的其他运动螺旋和使动螺旋的互易积为0的特点，利用反螺旋准则可以推导出该支链上可以存在的除驱动螺旋之外的其他运动螺旋系，据此即可推导出该支链所有可能存在的结构类型。

(4)根据并联机构约束螺旋综合理论，依次选择两条支链连接动静平台，即可获得期望的1T1R无耦合完全各向同性并联机构。

本文构造的无耦合完全各向同性并联机构的正逆雅可比矩阵均为对角阵，所以属于完全各向同性并联机构，同时机构的输出自由度是由独立的输入驱动提供的，即每条支链只含有一个驱动副，控制动平台的一个输出自由度，也满足完全解耦并联机构的结构特性。

4无耦合完全各向同性1T1R并联机构型综合

在构型综合过程中，假设第一条支链只提供动平台沿Z轴方向的移动驱动，第二条支链只提供动平台绕Z轴方向的转动驱动。下面根据上述构型原理分别给出两条支链的构型过程。

4.1第一条支链的型综合过程

假设第一条支链只提供沿Z轴方向的移动驱动，正雅可比矩阵中第一行只有一个非零元素[Jr]11。可知驱动副作用于动平台上的使动螺旋为力线矢螺旋，设使动螺旋的形式为$a1=[l1m1n1;p1q1r1]，由于使动螺旋只对动平台沿Z轴方向有驱动力，所以设$a1=[0 0n1;p1q10]，其他的情况不符合要求。设使动螺旋过动平台上一点(p1,q1,r1)，根据式(1)可得$a1=[0 0 1;q1p10]，为简化分析，下文出现的螺旋均作单位螺旋处理。

4.1.1驱动副为沿Z轴方向的移动副

设支链中驱动副的螺旋表达形式为$q1=[a1b1c1;d1e1f1]，此时有：

[Jv]11=$q1∘$a1=f1+a1q1+b1p1

(12)

若需[Jv]11为常数，则a1、b1需等于0。即$q1存在以下两种情况：

(13)

将式(13)代入式(12)，有：

(14)

由式(14)可知，第一种情况不满足要求，所以有：

(15)

综上所述有：

(16)

4.1.2驱动副为2R平行子链的转动副

当并联机构分支驱动为移动驱动时，可以用一个垂直于原驱动方向的由两个轴线平行的转动副构成的2R平行子链来替代该驱动副。如果驱动副为轴线沿Z轴方向的移动副，则可用两个轴线沿X轴或Y轴方向的转动副构成的2R平行子链替代原移动驱动，此时该分支将不仅对Z轴方向具有驱动力作用，而且对Y轴方向也将具有驱动力作用，此处将这种对Y轴方向的驱动力称为消极驱动。为了不破坏原有机构的稳定结构和解耦特性，在该支链的结构螺旋系中一定要存在一个与该支链中消极驱动方向共线的一个移动副，以消除该消极驱动对机构自由度的影响。

4.1.2.1驱动副为沿X轴方向的转动副

当用两个轴线平行于X轴方向的转动副构成的2R平行子链代替Z轴方向的移动驱动时，根据前述分析，可知驱动螺旋$q12=[1 0 0; 0e12f12]，此时有：

(17)

由于点(p1,q1,r1)是动平台上任意一点(与坐标系设置有关)，所以当取q1=0时，式(17)写为

(18)

f12为驱动副的螺旋表达参数，由于本文中驱动副均与固定基座相连，所以其螺旋参数不发生改变，即f12为定值，即[Jv]11-1为定值，满足要求。

4.1.2.2驱动副为沿Y轴方向的转动副

当用两个轴线平行于Y轴方向的转动副构成的2R平行子链代替Z轴方向的移动驱动时，可知驱动螺旋$q13=[0 1 0;d130f13]，此时有：

(19)

同理当取p1=0时，式(19)写为

(20)

具体分析过程同4.1.2.1节，可知此种情况下也满足要求。

4.1.3支链结构螺旋系

确定了支链的使动螺旋和驱动螺旋之后，根据反螺旋定理可得到支链中除驱动螺旋之外的其他可能存在的运动螺旋系。由式(2)和反螺旋定理[15]可知支链上满足条件的运动螺旋系有：

(1)与Z轴方向平行的线矢量螺旋系，此类螺旋在支链中至少有1个，最多有3个；

(2)与Z轴方向垂直的偶量螺旋系，这类螺旋在支链中最多为2个，且方向互不平行。

由文献[17]知并联机构支链必含动平台的运动特征，所以文中支链结构螺旋系至少为1T1R形式。其中R代表转动副，T代表移动副，R和T为基本运动副，运动副下带有下划线表示驱动副，限于篇幅，本文只考虑基本运动副的情况，其他的复合运动副替代基本运动副的情况可参阅文献[3]。下标X、Y、Z表示运动副的轴线方向，下标N表示轴线垂直于Z轴，为简化结构，假设相邻运动副轴线均垂直或平行，在实际工程应用中则不然，可根据具体情况予以设计考虑。根据本节对于支链驱动类型的分析，将支链一分为三类，分别对应4.1.1节、4.1.2.1节、4.1.2.2节中三种类型的驱动类型。具体的支链一结构如表1所示。

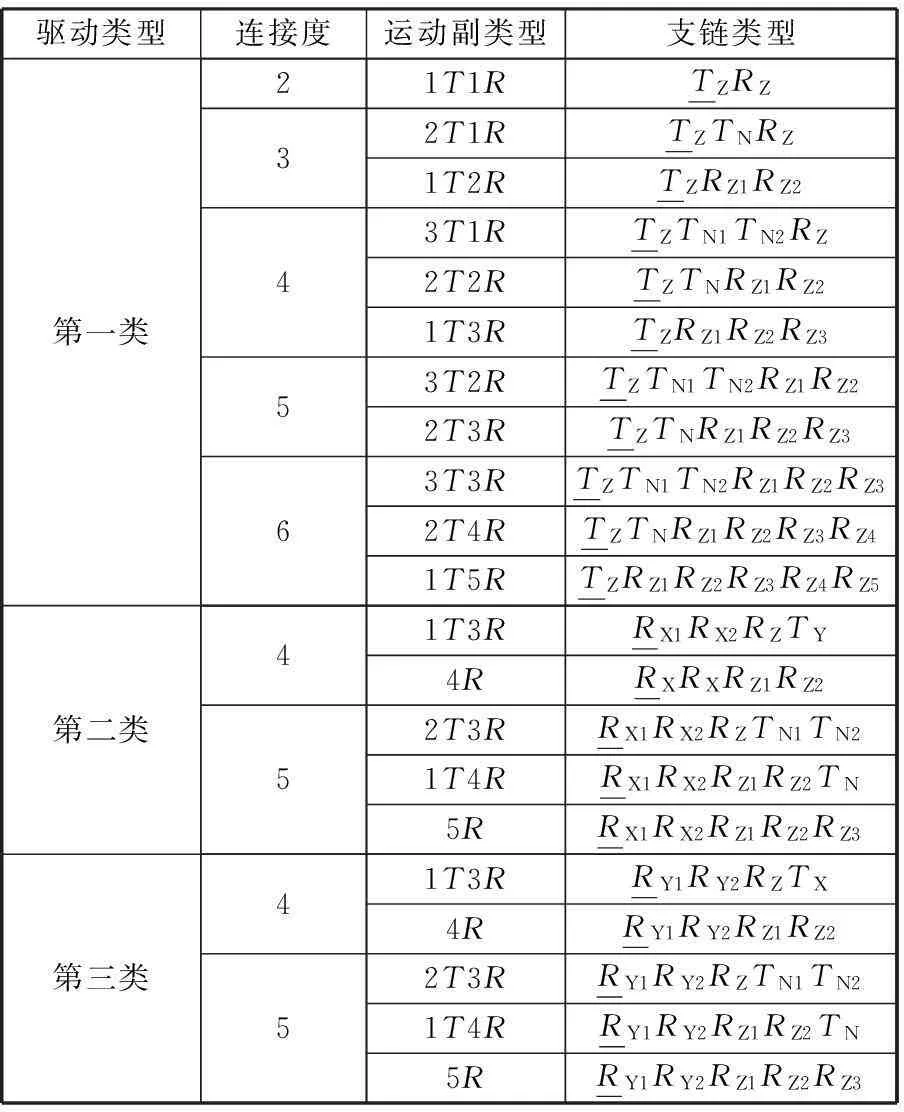
表1　第一条支链结构

4.2第二条支链的型综合过程

假设第二条支链只提供对Z轴方向的转动驱动，支链驱动作用于动平台上的使动螺旋为力矩螺旋。由于期望动平台只有绕Z轴方向的转动自由度，而机构由两条支链组成，所以当第二条支链的使动螺旋在任何不平行于Z轴的方向上有分量时，可能会导致机构具有其他方向的运动特征。所以根据支链独立驱动原则，这里使动螺旋的形式只能为

(21)

设第二条支链上表示驱动副的驱动螺旋$q2=[a2b2c2;d2e2f2]。由于分支中可能具有沿X、Y方向的运动特征，但期望动平台只具有沿Z轴的运动特征，所以当驱动螺旋沿X、Y方向具有分量时，可能会导致动平台具有沿X、Y方向的自由度，所以这里驱动螺旋$a2=[0 0 1;d2e20]。此时有：

(22)

由式(22)可得

(23)

确定了支链作用于动平台上的使动螺旋和驱动螺旋之后，可以根据反螺旋定理得到支链中可以存在的除驱动螺旋之外的其他运动螺旋系。由式(2)和反螺旋定理[15]可知，满足条件的螺旋系有：

(1)任意方向的偶量螺旋系。任意两个偶量的轴线不平行，此类螺旋在支链中最多有3个，且支链中至少存在一个轴线平行于Z轴的偶量。

(2)与使动螺旋的轴线垂直的线矢量螺旋系。当数目为2～3个时，其轴线需相互平行；当数目等于或多于4个时，需分为两组，每组内的螺旋轴线相互平行。

由以上分析可得到第二条支链结构如表2(运动副的含义同上节)所示。

4.31T1R并联机构型综合

对于并联机构的综合方法，有基于运动特征的综合方法[17]，也有利用约束螺旋理论的综合方法[3]。本文结合两种方法的分析原理，将综合的1T1R并联机构分为两类。

(1)第一种类型，根据并联机构运动特征原理得到。选取支链一时只选择表1中的第一类支链，此时构成的并联机构中至少有一条支链的连接度为2。另根据文献[8]研究可知，组合支链时需注意以下准则：转动解耦并联机构转动条件为两分支需提供垂直于Z轴的两个不共线的移动自由度。结合以上分析可知，当一条的连接度选取为2时，另一条支链的选取需符合以下准则：连接度至少为4，且需具有垂直于Z轴的二维移动特征。由于构造的并联机构类型较多，在此不再列表赘述。

(2)第二种类型，支链一的结构类型将从表1中的第二类和第三类中选择，此时需根据并联机构的约束螺旋综合法选取第二条支链，由于约束螺旋综合法中主要综合的是对称的并联机构，而关于不对称的并联机构则和机构的尺寸综合有关，在此就不再讨论这种情况，仅从第二条支链中选取连接度为2的支链，再选取符合1T1R并联机构转动条件的第一条支链构造并联机构，其具体构型结果如表3所示。

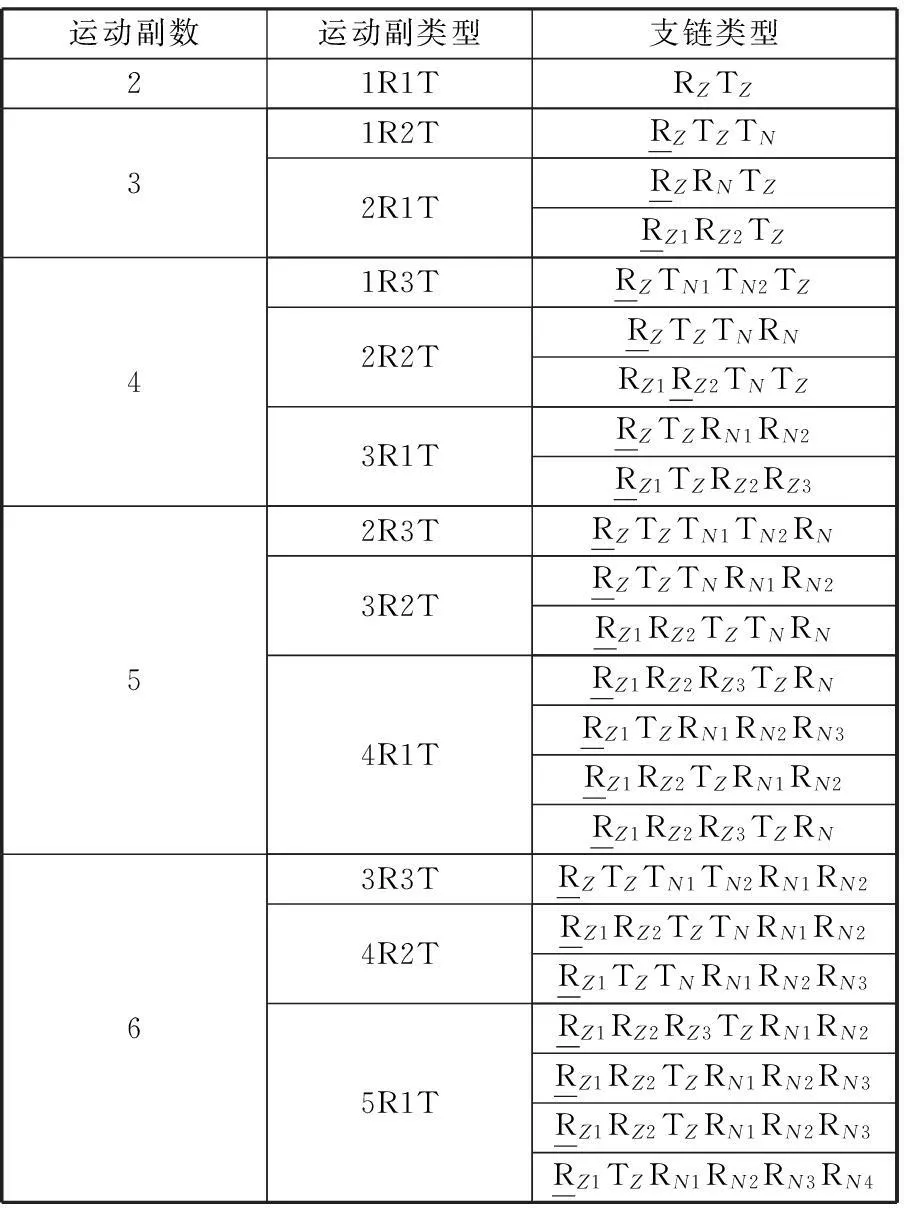
表2　第二条支链结构

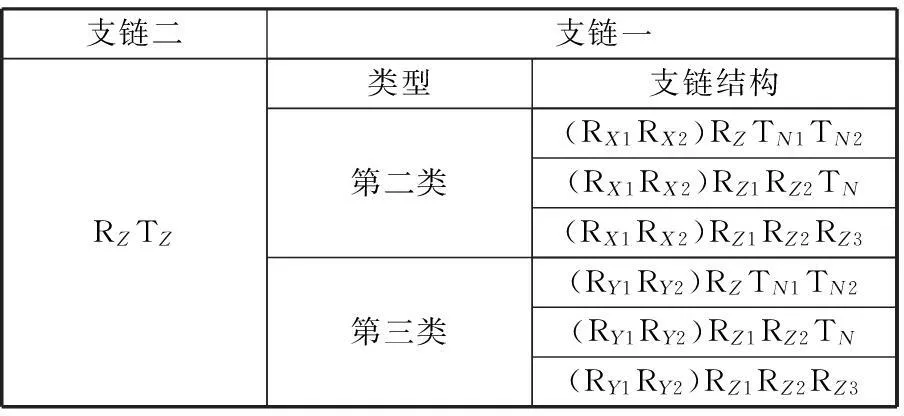
表3　第二类无耦合完全各向同性并联机构

至此，即完成了1T1R并联机构的型综合过程，得到了大量无耦合完全各向同性1T1R并联机构，而且包括6类完全由转动驱动构成的新型机构。本文综合的两条支链第一个运动副取为驱动副，且直接与基座相连，其在支链中的位置不能变动，由转动副构成的2R平行子链间不能存在其他运动副。如果用复合副替代基本运动副，或改变支链中运动副的顺序，则可以得到更多的并联机构，具体方法可参看文献[17]。图1和图2所示为根据构型结果得到的两种无耦合完全各向同性1T1R并联机构。

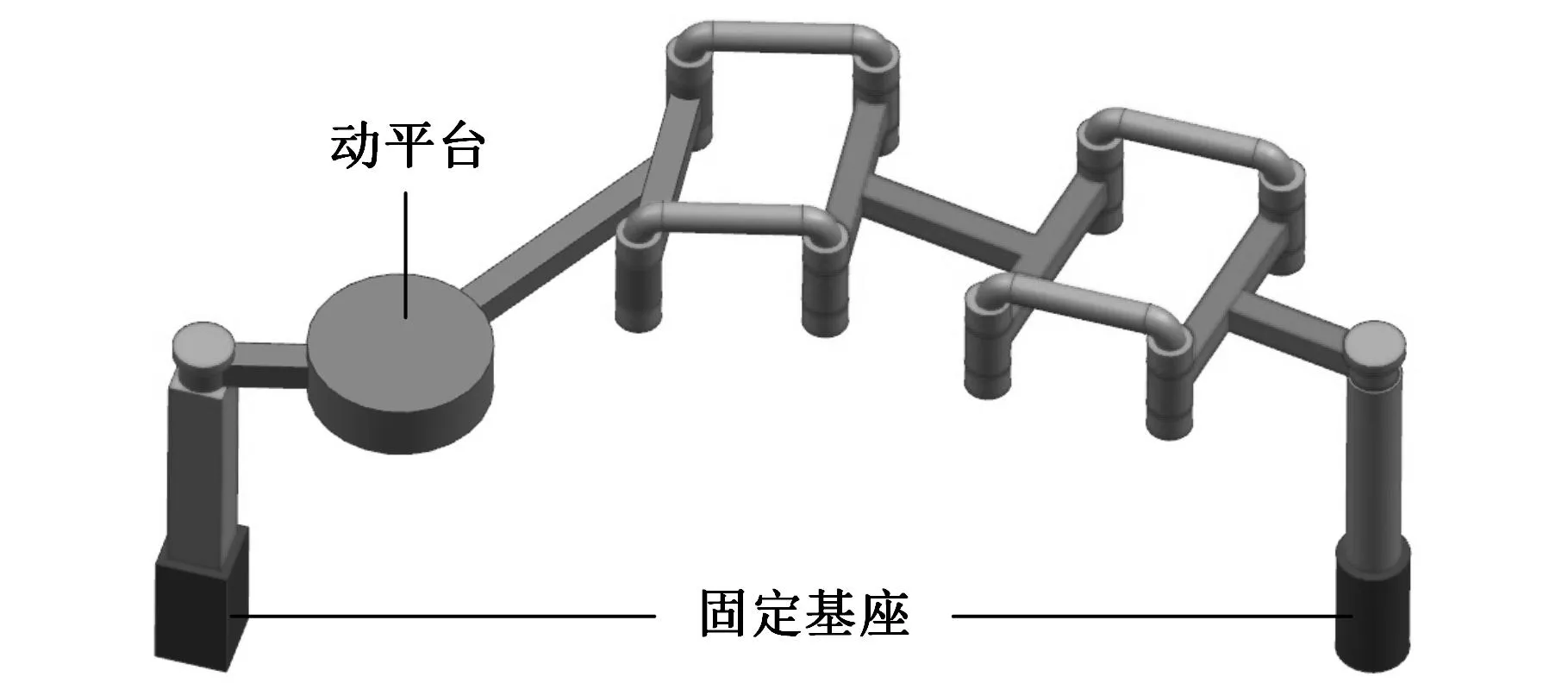
图-&-并联机构

图2　RZTZ-&-并联机构

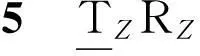
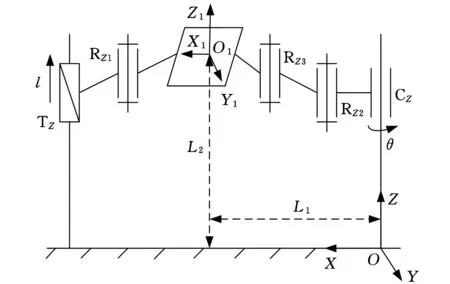
图-&-并联机构简图

5.1机构运动学分析

设动平台坐标系原点初始时刻坐标为O1(L1, 0, L2)，驱动副TZ驱动为l，圆柱副CZ输入角度θ。动平台沿基坐标系Z轴的移动距离为l1，转动角度为θ1(逆时针为正)，由机构运动学可知，基坐标系和动坐标系的齐次变换矩阵依次为

(24)

根据齐次坐标变换，动平台运动后，动坐标系原点坐标O2为

(25)

将式(24)代入式(25)中得O2=(L1cosθ1,L1sinθ1,L2+l), 可得机构使动螺旋为

(26)

又因为两条支链的驱动副固接于定平台，可得其驱动螺旋为

(27)

5.2机构雅可比矩阵求解

将式(26)和式(27)代入式(5)有：

(28)

即有：

(29)

由式(29)可知机构的雅可比矩阵相似于单位对角阵，所以机构为无耦合完全各向同性并联机构，验证了构型原理的正确性。

6总结与展望

(1)本文利用螺旋理论和约束螺旋综合法对无耦合完全各向同性1T1R并联机构进行了构型综合。通过分析完全解耦、完全各向同性并联机构的结构特性，可知当机构正逆雅可比矩阵均为对角阵时，机构雅可比矩阵满足无耦合、完全各向同性的要求。首先利用螺旋理论确定支链驱动作用于动平台上的使动螺旋和表示驱动副的驱动螺旋，其次根据互易螺旋得到各条支链的结构螺旋系，再据此配置支链的运动副结构，最后基于约束螺旋理论组合两条分支，得到大量无耦合完全各向同性1T1R并联机构，包括了6类完全由转动驱动构成的新型机构。

(2)本文综合的1T1R并联机构，具有完全解耦、完全各向同性的特点，所以这类并联机构控制简单，具有良好的运动学和力传递性能，在微操作机器人和医用机器人等领域具有潜在的应用前景。其中部分构型已申请中国发明专利。对于文中并联机构构型设计的应用，目前仍在理论分析阶段，对于实体样机的研制将在后续工作中继续开展。

参考文献：

[1]SimionescuL,CiupituL,LonitaLC.StaticBalancingwithElasticSystemsofDELTAParallelRobots[J].MechanismandMachineTheory, 2015, 87(5):150-162.

[2]LiQC,HuangZ,HervéJM.DisplacementManifoldMethodforTypeSynthesisofLower-mobilityParallelMechanisms[J].ScienceinChinaSeriesE:TechnologicalSciences, 2004, 6:641-650.

[3]HuangZ,LiQC.TypeSynthesisofSymmetricalLower-mobilityParallelMechanismsUsingtheConstraintSynthesisMethod[J].TheInternationalJournalofRoboticsResearch, 2003, 22(1):59-82.

[4]杨廷力. 机器人机构拓扑机构学[M]. 北京:机械工业出版社，2004.

[5]StewartD.APlatformwithSixDegreesofFreedom[J].ProceedingsoftheInstitutionofMechanicalEngineers, 1965, 66(15):371-386.

[6]ZhaoY,LiuJF,HuangZ.AForceAnalysisofa3-RPSParallelMechanismbyUsingScrewTheory[J].Robotica, 2011, 29(7):959-965.

[7]KongXW,GosselinCM.TypeSynthesisofInput-OutputDecoupledParallelManipulators[C]//TransactionsoftheCanadianSocietyforMechanicalEngineering, 2004, 28(2):185-196.

[8]ZengDX,HuangZ.TypeSynthesisoftheRotationalDecoupledParallelMechanismBasedonScrewTheory[J].Sci.ChinaTech.Sci., 2011, 54:998-1004.

[9]LegnaniG,FassiI,GibertiH.ANewIsotropicandDecoupled6-DOFParallelManipulator[J].MechanismandMachineTheory, 2012, 58:64-81.

[10]GoguG.StructuralSynthesisofFully-isotropicParallelRobotswithSchonfliesMotionsViaTheoryofLinearTransformationsandEvolutionaryMorphology[J].EuropeanJournalofMechanicsA/Solids, 2006, 25:1-28.

[11]CarricatoM,Parenti-CastelliV.Singularity-freeFullyIsotropicTranslationalParallelMechanisms[J].InternationalJournalofRoboticsResearch, 2002, 21(2):161-174.

[12]GoguG.StructuralSynthesisofFully-isotropicTranslationalParallelRobotsViaTheoryofLinearTransformations[J].EuropeanJournalofMechanicsA/Solids, 2004, 23:1020-1039.

[13]CarricatoM.Fully-isotropicFour-degrees-of-freedomParallelMechanismsforSchoenfliesMotion[J].InternationalJournalofRoboticsResearch, 2005, 24(5):397-414.

[14]张彦斌, 吴鑫, 刘宏昭. 完全各向同性2T1R空间并联机器人机构型综合[J]. 农业机械学报, 2011, 42(11):200-207.

ZhangYanbin,WuXin,LiuHongzhao.StructuralSynthesisofFully-isotropic2T1RSpatialParallelManipulators[J].TransactionsoftheChineseSocietyforAgriculturalMachinery, 2011, 42(11):200-207.

[15]DuffyJ.TheScrewTheoryandItsApplication[M].Florida：ClassNoteofUniversityofFlorida, 1982.

[16]ZengDX,HouYL,LuWJ.TypeSynthesisMethodfortheTranslationalDecoupledParallelMechanismBasedonScrewTheory[J].JournalofHarbinInstituteofTechnology, 2014, 21(1): 84-91.

[17]高峰, 杨加伦, 葛巧德. 并联机器人型综合的GF集理论[M]. 北京:科学出版社, 2004.

(编辑袁兴玲)

Type Synthesis of Fully-decoupled and Fully-isotropic 1T1R Parallel Robotic Manipulators

Chen Hai1Cao Yi1,2,3Qin Youlei1

1.Jiangnan University,Wuxi,Jiangsu,214122

2.Jiangsu Key Laboratory of Advanced Food Manufacturing Equipment and Technology,Wuxi,Jiangsu,214122

3.State Key Laboratory of Mechanical System and Vibration,Shanghai Jiao Tong University,Shanghai,200240

Abstract:Based on the screw theory, a method of structural synthesis of fully-decoupled and fully-isotropic one-translational and one-rotational(1T1R) parallel mechanisms was proposed, the parallel mechanism adopted with driven-chain whose output link was provided by independent motors. Firstly, according to the prescribed characteristics of each mechanism limb, a methodology was proposed that made use of the screw theory to synthesize desired forms for both of the direct and the inverse Jacobian matrices. Secondly, according to the features both of the direct and the inverse Jacobian matrices, the actuation screws, actuated screws and mobile un-actuated screws of every limb were confirmed at first based on the reciprocal screw theory, and the leg structure was obtained. Then the structural synthesis of each kinematic chain for fully-isotropic 1T1R parallel robotic manipulators was performed in the light of different connectivities of the limbs. Finally, the anticipant manipulators were synthesized by using the rules and regulations of fully- isotropic parallel mechanisms and a lot of parallel mechanisms were obtained. Many of fully-decoupled and fully-isotropic 1T1R parallel mechanisms were synthesized by using the above method. Kinematical analysis about one of manipulators designed here show that the method is reasonable and correct.

Key words:screw theory；driven-chain； parallel mechanism；type synthesis

作者简介：陈海，男，1991年生。江南大学机械工程学院硕士研究生。主要研究方向为并联机器人机构学。曹毅，男，1974年生。江南大学机械工程学院副教授、博士，上海交通大学机械系统与振动国家重点实验室访问学者。秦友蕾，男，1991年生。江南大学机械工程学院硕士研究生。

中图分类号：TH112

DOI：10.3969/j.issn.1004-132X.2016.05.004

基金项目：国家自然科学基金资助项目(50905075)；江苏省普通高校学术学位研究生科研创新计划项目(KYLX-1115)；机械系统与振动国家重点实验室开放课题资助项目(MSV201407)

收稿日期：2015-05-05