基于解析模态分解的机械故障诊断方法

时培明　苏翠娇　赵　娜　韩东颖

1.燕山大学河北省测试计量技术及仪器重点实验室,秦皇岛,0660042.燕山大学,秦皇岛,066004



基于解析模态分解的机械故障诊断方法

时培明1,2苏翠娇1,2赵娜1,2韩东颖2

1.燕山大学河北省测试计量技术及仪器重点实验室,秦皇岛,0660042.燕山大学,秦皇岛,066004

摘要：针对旋转机械故障诊断问题，提出了一种基于解析模态分解(AMD)的旋转机械故障诊断方法。只要知道信号的频率成分，AMD方法就可以将含不同频率成分的信号分解为单频率信号，尤其能够分解有紧密间隔频率成分的信号。对于可预知故障特征频率的旋转机械的故障诊断，可利用AMD方法提取机械振动信号中故障特征频率所在频段的信号，并求该段信号的频谱，若频谱中含有故障特征频率，则说明机械振动信号中存在该故障。通过对滚动轴承故障信号和转子不对中故障信号的分析以及和经验模态分解(EMD)方法的对比，证明了AMD方法的有效性，且AMD方法比EMD方法更快速、准确。

关键词：解析模态分解；信号提取；故障诊断；旋转机械

0引言

旋转机械设备在工业生产中占有非常重要的地位，保障旋转机械的安全运行是非常重要的，因此对旋转机械进行故障诊断具有重要现实意义[1-4]。目前，旋转机械故障诊断的方法非常多，如经验模态分解(EMD)、小波分析、神经网络及包络解调等。文献[4]将EMD方法应用于旋转机械故障诊断，但EMD方法存在的模态混叠、端点效应问题会影响分析结果；文献[5]利用小波脊线的解调方法对故障进行诊断，但该方法主要针对单分量信号，而大多数旋转机械的故障信号是多分量的，因此，使用该方法处理前还需要通过带通滤波将多分量信号分解成单分量信号。

解析模态分解法(analytical mode decomposition，AMD)是Chen等[5]提出的一种新的信号分解方法，该方法可从信号中分离出各种频率成分的信号，但前提是需要确定信号里的各个频率成分，进而确定二分频率值进行AMD分解。文献[6]使用AMD分离出了温度对桥梁的影响，其二分频率是通过分析能量分布确定的。对于一些旋转机械，其不同部位的故障特征频率是可以预先计算出来的，所以可以用AMD方法对机械振动信号进行处理来判断是否含故障频率成分。

本文将AMD方法应用到滚动轴承故障诊断中，因为滚动轴承故障频率是可预知的[7-8]，可利用AMD方法分离出该频段的信号并求其频谱，通过观察是否含故障频率来判断轴承是否出现故障，又通过转子不对中故障进一步验证了本方法的优越性。文中使用AMD方法与EMD方法对同一轴承故障信号和转子不对中数据进行分析处理。实验结果表明，AMD方法能够实现对旋转机械的故障诊断，且比EMD方法更快速、准确。

1解析模态分解法

解析模态分解法[5]可以将含有不同频率成分的信号分解为单分量信号，尤其能够分解有紧密间隔频率成分的信号。

若一个时间序列x(t)被二分频率ωb分成两个信号和：

(1)

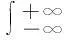
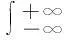
(2)

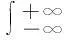
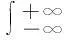
(3)

令sc(t)=cos(ωbt)，ss(t)=sin(ωbt)，sk(t)x(t)(k=c,s)的希尔伯特变换为

(4)

根据Bedrosian定理，式(4)可以写成

(5)

k分别取c和s建立联立方程式，可解得

(6)

(7)

sc(t)和ss(t)的希尔伯特变换可以表示为

H[sc(t)]=sin(ωbt)H[ss(t)]=-cos(ωbt)

所以

ss(t)H[sc(t)]-sc(t)H[ss(t)]=1

(8)

则式(6)和式(7)写成

s1(t)=sin(ωbt)H[x(t)cos(ωbt)]-

cos(ωbt)H[x(t)sin(ωbt)]

(9)

cos(ωbt)H[x(t)cos(ωbt)]

(10)

由式(1)得

(11)

(12)

2基于AMD的故障诊断方法

2.1AMD信号提取算法

Feldman[9]进一步对该分解方法做出新的解释，它可以作为低通滤波使用。由于AMD方法可以把一个时间序列分解成任意两个信号的和的形式，所以，AMD分解方法不仅可以实现低通滤波的功能，还可以对任何频率成分的信号进行提取，但是需要知道原信号的频率成分。

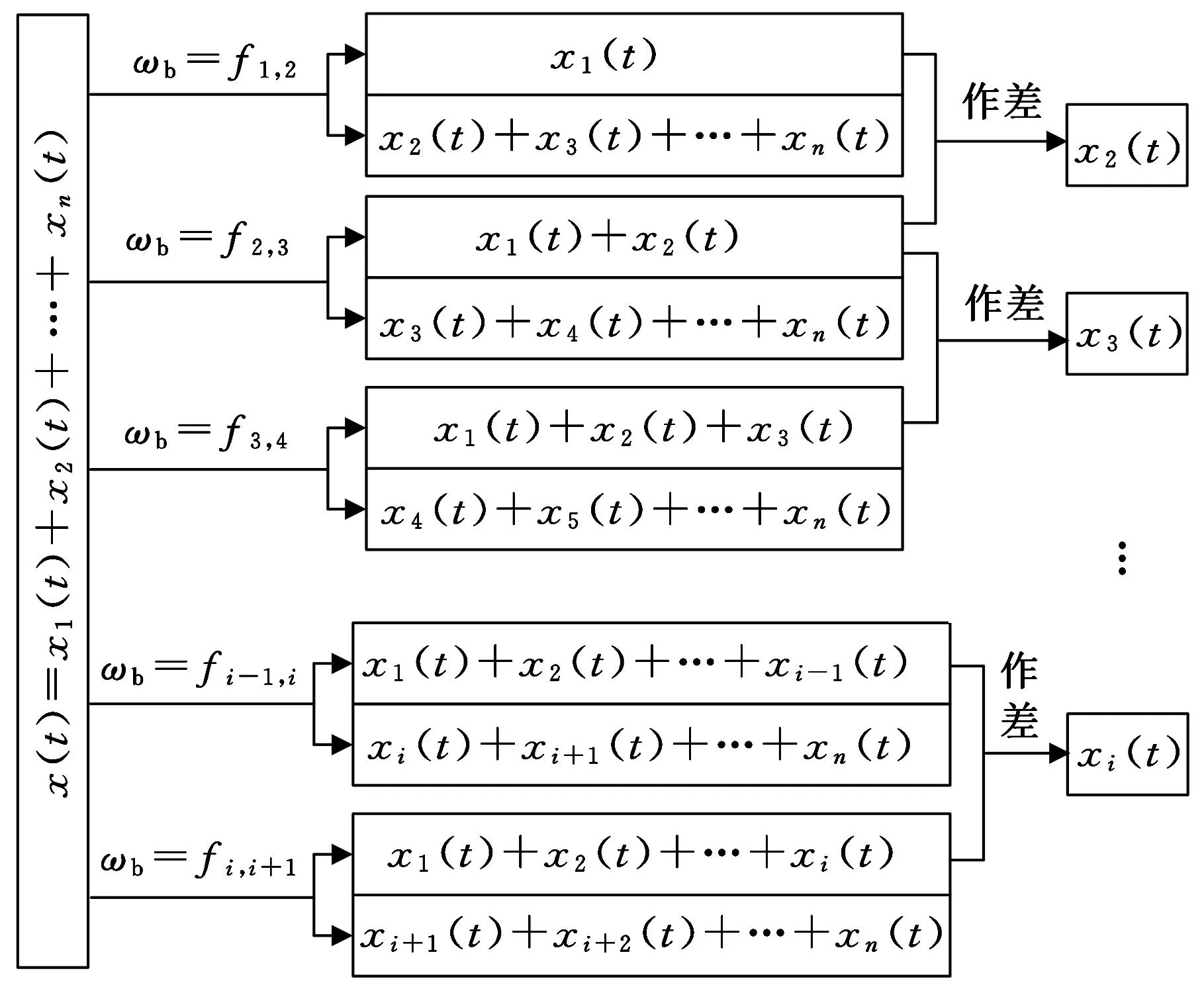
假设有一时间序列：x(t)=x1(t)+x2(t)+…+xn(t)，其频率分别为f1,f2,…,fn且f1

图1　AMD提取信号原理图

2.2旋转机械故障诊断方法

针对旋转机械故障中可以预知故障特征频率的情况，提出了一种基于AMD的旋转机械故障诊断方法。该方法通过AMD提取振动信号中故障特征频率所在频段的信号，并求该段信号的频谱，判断信号中是否存在故障以及故障类型。该方法具体步骤如下：

(1)若某旋转机械中可能存在的故障频率为f1,f2,…,fn，对原振动信号进行AMD分解，提取出各个故障频率所在频段的信号；

(2)求出所有提取出的信号的频谱，判断频谱中是否有故障特征频率成分；

(3)将信号频谱中有故障特征频率的保留，将频谱中不含故障特征频率的去除；

(4)经AMD提取出的各个信号中含有的故障特征频率为f1,f2,…,fm，根据所含频率成分判断旋转机械是否存在故障以及发生故障的部位。

AMD故障诊断方法的处理过程如图2所示。

图2　AMD故障诊断流程图

3应用实例

滚动轴承包括内圈、外圈、滚动体和保持架等四部分，其故障频率与转速和滚动轴承的结果参数有关。如果滚动轴承发生故障，其故障频率是可预知的[7-8]。在假设滚动轴承的外圈固定，内圈转动情况下，工作轴转速为n(r/min)、轴承节径为D(mm)、滚动体直径为d(mm)、接触角为β(rad)、滚动体个数为N，则其不同故障特征频率如下[7-8]：

轴承外圈有缺陷时的特征频率为

(13)

轴承内圈有缺陷时的特征频率为

(14)

单个滚动体有缺陷时的特征频率：

(15)

保持架与外圈发生碰磨时的特征频率为

(16)

以美国西储大学实验台数据为例进行分析，其驱动端轴承型号为SKF6205，轴承转速为1797r/min(29.95Hz)，采样频率为12kHz。轴承节径为39.04mm，滚动体直径为7.94mm，滚动体数量为9，接触角为0°。经计算保持架故障频率为12Hz，外圈故障频率为107Hz，内圈故障频率为162Hz，滚动体故障为141Hz。

下面对一个含内圈故障的滚动轴承数据进行分析处理。轴承故障信号的时域波形如图3所示。对该信号直接进行EMD分解，分解结果如图4所示。故障信号经过EMD方法处理后，分解成了12个内禀模态函数(IMF)分量和一个余量。

图3　轴承内圈故障信号时域图

图4　轴承内圈故障信号EMD分解结果

对EMD分解出的每个分量求其频谱，分量的频谱如图5所示，由于后面几个分量的频率非常低，这里只显示前9个IMF的频谱。从图5可以看出，IMF6包含了故障的特征频率162Hz，幅度为0.008 621m/s2，而且在IMF6的频谱中还存在其他的频率成分，这是由于噪声等因素的影响使EMD分解存在模态混叠的问题，导致分量中含有多个频率成分[10-11]。

图5　图4中IMF分量的频谱图

下面用本文所提方法对滚动轴承故障信号进行处理。轴承故障频率是可预知的，令f1、f2、f3、f4分别对应保持架故障频率12Hz、外圈故障频率107Hz、滚动体故障141Hz和内圈故障频率162Hz。

利用AMD方法依次提取f1、f2、f3、f4所在频段的信号，提取出的信号时域波形如图6所示。对提取的4个信号分别求其频谱，如图7所示。

图6　AMD提取信号的时域图

图7　AMD提取信号的频谱图

从图6可以看出，故障特征频率f1、f2、f3所在频段的振动信号十分微弱，图7中，其频谱中几乎没有频率成分，因此可以认为信号中没有f1、f2、f3的频率成分，即滚动轴承的保持架、外圈及滚动体没有故障。而提取出的f4所在频段的信号明显增强，且其频谱中的频率成分为162Hz，幅度为0.014 68m/s2，符合内圈故障的特征频率。因此，滚动轴承的内圈存在故障。

经本文所提方法处理后，诊断出了滚动轴承发生故障的部位，且与实际情况相符。和EMD方法相比，经本文方法处理后的故障信号频谱中的频率成分更单一，且故障频率的幅度也有所增加。在处理过程中，由于实际信号中含有高频噪声以及其他噪声成分， 使EMD分解出的前几个分量均为噪声成分，大大增加了分量个数，因此，延长了实际信号的整个处理过程。而AMD方法只针对故障特征频率成分进行处理，略去了对其他不相关频率成分信号的分析处理，使处理速度加快，缩短了处理时间。

为了进一步验证本文所提方法的工程实用性，通过一组含转子不对中故障数据的特征提取及诊断进行检验。图8是一个含转子不对中故障的振动信号，转速为900r/min(15Hz)，采样频率为768Hz。

图8　转子不对中故障信号时域图

对该故障信号进行EMD分解，取前5个分量并求各分量频谱，分解结果和频谱分别如图9和图10所示。从中可以看出IMF3和IMF4分量分别对应着故障信号的二倍频和基频振动模态，但噪声的存在，使分量频率成分复杂且二倍频和基频成分容易湮没在噪声中，不易被识别。

图9　转子不对中故障信号EMD分解结果

图10　图9中IMF分量的频谱图

下面用AMD方法对转子不对中故障信号进行处理，分别提取基频和二倍频所在频段的信号并求其频谱，提取出的信号时域波形和频谱分别如图11和图12所示，从图中可看出基频和二倍频的值更加精确单一且幅值也有很大程度的提升。

图11　转子不对中故障信号AMD提取信号的时域图

图12　转子不对中故障信号AMD提取信号的频谱图

4结论

(1)提出一种基于AMD的旋转机械的故障诊断方法。由于一些旋转机械故障频率是可预知的，因此可以利用AMD方法提取故障频段的信号并求其频谱，以此来判断提取的信号中是否有故障频率，进而判断旋转机械是否存在故障以及故障发生的部位。

(2)对含内圈故障的滚动轴承振动信号和转子不对中故障数据的分析处理证明了本文方法可以提取出信号的故障特征频率，说明该方法能够实现对旋转机械的故障诊断。通过与EMD方法的比较，表明了应用AMD方法对旋转机械故障诊断更加快速、准确。

参考文献：

[1]杨宇, 于德介, 程军圣. 基于经验模态分解的滚动轴承故障诊断方法[J]. 中国机械工程, 2004,15(10): 908-920.

YangYu,YuDejie,ChengYunsheng.RollerBearingFaultDiagnosisMethodBasedonEMD[J].ChinaMechanicalEngineering, 2004, 15(10):908-920.

[2]王翔, 王仲生. 基于改进Hilbert-Huang变换的转子碰摩故障诊断[J]. 中国机械工程, 2010, 22(24): 2937-2940.

WangXiang,WangZhongsheng.IncipientRub-impactFaultDiagnosisofRotorSystemUsingImprovedHHT[J].ChinaMechanicalEngineering, 2011, 22(24):2937-2940.

[3]时培明, 李庚, 韩东颖. 基于改进EMD的旋转机械耦合故障诊断方法研究[J]. 中国机械工程, 2013, 24(17): 2367-2372.

ShiPeiming,LiGeng,HanDongying.StudyonCouplingFaultsofRotaryMachineryDiagnosisMethodbasedonImprovedEMD[J].ChinaMechanicalEngineering, 2013, 24(17):2367-2372.

[4]WuF,QuL.AnImprovedMethodforRestrainingtheEndEffectinEmpiricalModeDecompositionandItsApplicationstotheFaultDiagnosisofLargeRotatingMachinery[J].JournalofSoundandVibration, 2008, 314(3): 586-602.

[5]ChenG,WangZ.ASignalDecompositionTheoremwithHilbertTransformandItsApplicationtoNarrowbandTimeSerieswithCloselySpacedFrequencyComponents[J].MechanicalSystemsandSignalProcessing, 2012, 28: 258-279.

[6]李苗, 任伟新, 胡异丁, 等. 基于解析模态分解法的桥梁动态应变监测数据温度影响的分离[J]. 振动与冲击,2012, 31(21): 6-10.

MiaoLi,RenWeixin,HuYiding,etal.SeparatingTemperatureEffectfromDynamicStrainMeasurementsofABridgeBasedonAnalyticalModeDecompositionMethod[J].JournalofVibration&Shock, 2012, 31(21): 6-10.

[7]康守强, 王玉静, 杨广学, 等. 基于经验模态分解和超球多类支持向量机的滚动轴承故障诊断方法[J]. 中国电机工程学报, 2011, 31(14): 96-102.

KangShouqiang,WangYujing,YangGuangxue,etal.RollingBearingFaultDiagnosisMethodUsingEmpiricalModeDecompositionandHypersphereMulticlassSupportVectorMachine[J].ProceedingsoftheCSEE, 2011, 31(14):96-102.

[8]崔玲丽, 康晨晖, 胥永刚, 等. 滚动轴承早期冲击性故障特征提取的综合算法研究[J]. 仪器仪表学报, 2010, 31(11): 2422-2427.

CuiLingli,KangChenhui,XuYonggang,etal.IntegratedAlgorithmResearchonEarlyImpactiveFaultFeatureExtractionofRollingBearings[J].ChineseJournalofScientificInstrument, 2010, 31(11): 2422-2427.

[9]FeldmanM.ASignalDecompositionorLowpassFilteringwithHilbertTransform[J].MechanicalSystemsandSignalProcessing, 2011, 25(8): 3205-3208.

[10]时培明, 李庚, 韩东颖, 等. 基于延拓和窗函数的HHT端点效应改进方法[J]. 计量学报, 2013, 34(5): 491-496.

ShiPeiming,LiGeng,HaiDongying,etal.ExtensionandWindowFunctionBasedImproveMethodforEndEffectsofHilbert-HuangTransform[J].ActaMetrologicaSinica, 2013, 34(5): 491-496.

[11]汤宝平, 董绍江, 马靖华. 基于独立分量分析的EMD模态混叠消除方法研究[J]. 仪器仪表学报, 2012, 33(7): 1477-1482.

TangBaoping,DongShaojiang,MaJinghua.StudyontheMethodforEliminatingModeMixingofEmpiricalModeDecompositionBasedonIndependentComponentAnalysis[J].ChineseJournalofScientificInstrument, 2012, 33(7): 1477-1482.

(编辑袁兴玲)

Fault Diagnosis Method for Rotating Machinery Based on AMD

Shi Peiming1,2Su Cuijiao1,2Zhao Na1,2Han Dongying3

1.Key Laboratory of Measurement Technology and Instrumentation of Hebei Provnice,YanshanUniversity,Qinhuangdao,Hebei,066004

2.Yanshan University,Qinhuangdao,Hebei,066004

Abstract:Aiming at the problems of fault diagnosis for rotating machinery, a fault diagnosis method for rotating machinery was proposed based on AMD herein. As long as the frequency components of signals were known, signals with different frequency components might be decomposed into single frequency signals using the AMD method, especially to decompose a signal with closely spaced frequency components. For the fault feature frequency prediction in rotating machinery fault diagnosis, AMD method might be used to extract fault feature frequency signals in mechanical vibration signals and the frequency spectrum was obtained. If the frequency spectrum contains the fault feature frequency, it shows that the faults exist in mechanical vibration signals. The analysis of the rolling bearing fault signals and the comparison with empirical model decomposition(EMD), it shows that the AMD method is effective and more rapid, accurate than EMD.

Key words：analytical mode decomposition(AMD); signal extraction; fault diagnosis; rotating machinery

作者简介：时培明,男,1979年生。燕山大学电气工程学院副教授。主要研究方向为信号处理、故障诊断。发表论文30余篇。苏翠娇,女,1989年生。燕山大学电气工程学院硕士研究生。赵娜,女,1989年生。燕山大学电气工程学院硕士研究生。韩东颖,女,1978年生。燕山大学车辆与能源学院副教授。

中图分类号：TH165; TN911.7

DOI：10.3969/j.issn.1004-132X.2016.05.018

基金项目：国家自然科学基金资助项目(51475407)；河北省自然科学基金资助项目(E2015203190)；河北省高等学校自然科学研究重点项目(ZD2015050)

收稿日期：2015-05-07