中介轴承随机参数对双转子系统特征值的影响

孟　华　刘保国　李鸽鸽

1.商丘工学院，商丘，476000　　2.河南工业大学，郑州， 450007



中介轴承随机参数对双转子系统特征值的影响

孟华1刘保国2李鸽鸽2

1.商丘工学院，商丘，4760002.河南工业大学，郑州， 450007

摘要：通过复杂转子系统的随机参数运动微分方程，分析了转子系统特征值的随机性问题。通过整体传递矩阵法计算出双转子系统的特征值，使用Monte Carlo数值模拟计算方法，分别计算并分析了以具有一个中介轴承支撑和两个中介轴承支撑的双转子系统耦合单元的质量参数、刚度参数及阻尼系数为随机参数时，双转子系统的特征值均值及其标准差随变异系数的变化规律。

关键词：双转子系统；中介轴承；随机参数；特征值

0引言

1转子系统随机参数运动微分方程

许多转子系统的材料特性、载荷、几何参数、边界条件等参数都具有一定的随机性[3]，这使系统各零部件的质量、刚度、阻尼等参数也具有随机性，整个转子系统的随机参数运动微分方程可用下式表示：

(1)

(2)

若系统有n个随机参数，式(1)中的随机质量、刚度和阻尼矩阵可以用下式表示：

(3)

(4)

(5)

(6)

由此可以求得系统的特征值。由于系统的质量，刚度和阻尼都为随机量，所以系统的特征值也是随机的。

为了研究双转子系统中的中介轴承的随机参数对系统特征值的影响，将轴承的刚度和阻尼随机参数矩阵表示为[6]

(7)

(8)

2双转子系统的随机特征值

本文以单个中介轴承有阻尼轴对称双转子系统和两个中介轴承无阻尼轴对称双转子系统为研究对象[7]，分析参数的随机性对系统特征值的影响。

面板数据通过平稳性检验后才能进行协整检验，以确保建立面板数据模型的变量间存在长期的均衡关系。由单位根检验结果可知，4个变量都为0阶单整，因此可以进行协整性检验。本文采用 Kao 检验［20］、 Pedroni检验［21］、 Fish 检验 3种方法进行协整检验，若3种方法中有2种及以上通过检验，则认为变量间存在长期协整关系。检验结果如表3、4所示。检验结果显示，除了Kao检验统计值的P值大于0.1之外，Pedroni检验、Fish检验的各项检验统计量的P值都小于0.05，综合3种检验结果，认为4个变量之间存在长期的协整关系，可以进一步进行回归分析。

模型1是单个中介轴承有阻尼轴对称双转子系统，如图1所示，整个系统由内外两个转子组成，轴承A1、轴承B1为支撑内转子运转的支承轴承，C1为支承外转子运转的支撑轴承，内外转子由中介轴承D1连接。

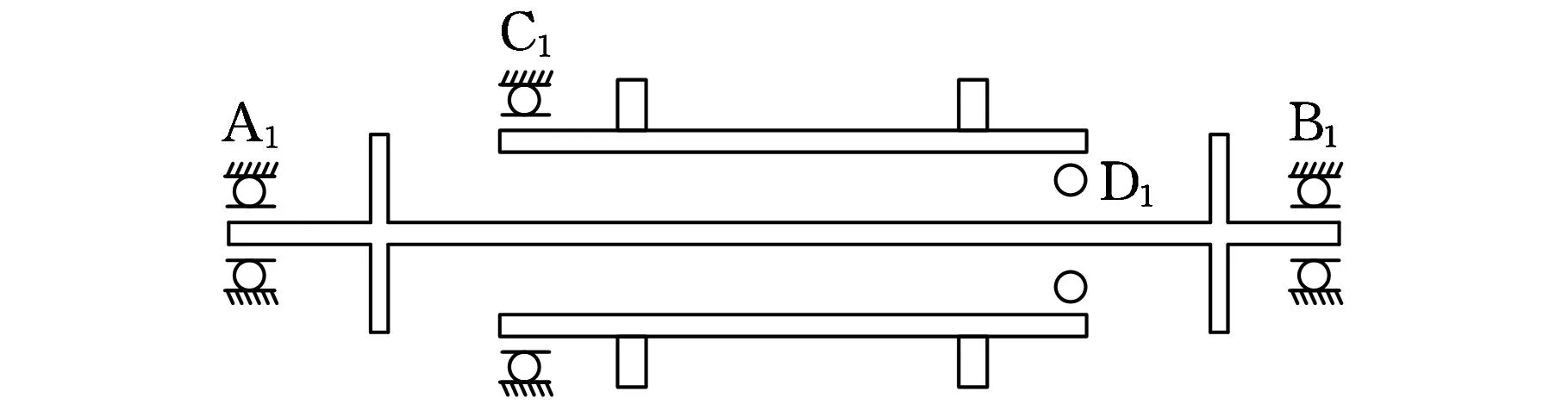
图1　单个中介轴承的双转子系统的结构示意图

模型2是两个中介轴承无阻尼轴对称双转子系统，如图2所示，系统由内外两个转子组成，轴承A2、轴承B2为支承内转子运转的支承轴承，内外转子由两中介轴承C2、D2连接。

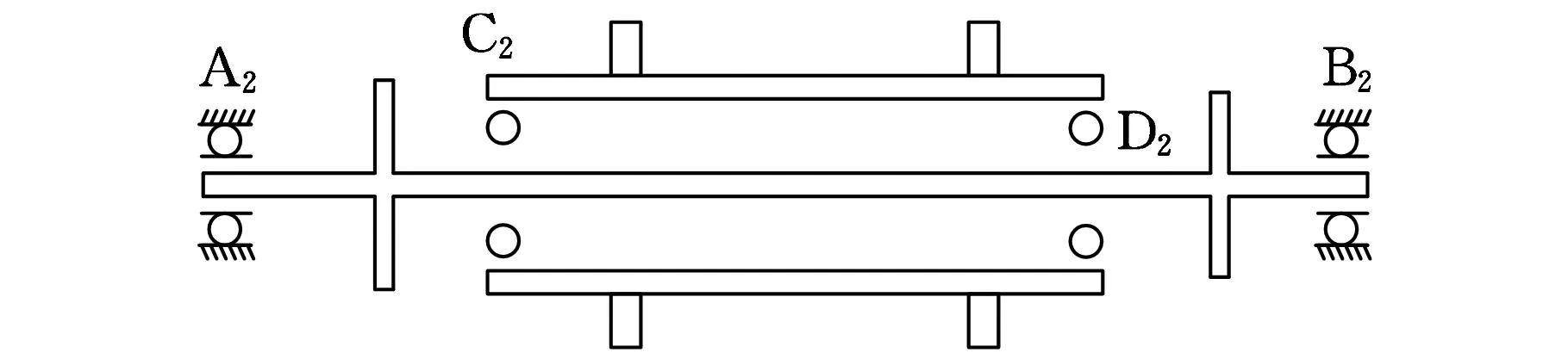
图2　两个中介轴承的双转子系统的结构示意图

中介轴承的质量、刚度和阻尼参数都服从正态分布，使用MonteCarlo方法[8]抽样计算一万次，分别计算出变异系数ε在0.01～0.30间取值时系统特征值的最大值、最小值、平均值及标准差。利用整体传递矩阵法计算两种确定性模型的前三阶特征值，如表1所示。

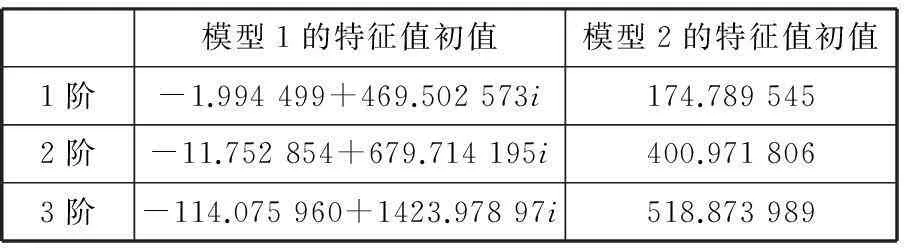
表1　两种轴承-双转子系统模型的初始特征值

2.1模型1的随机特征值

模型1的计算模型如图3所示，根据整个双转子系统的结构特点，将其划分为8个轴段，10个节点。在整个转子系统中，轴承的刚度和阻尼系数如表2所示，各轴段的结构信息如表3所示。

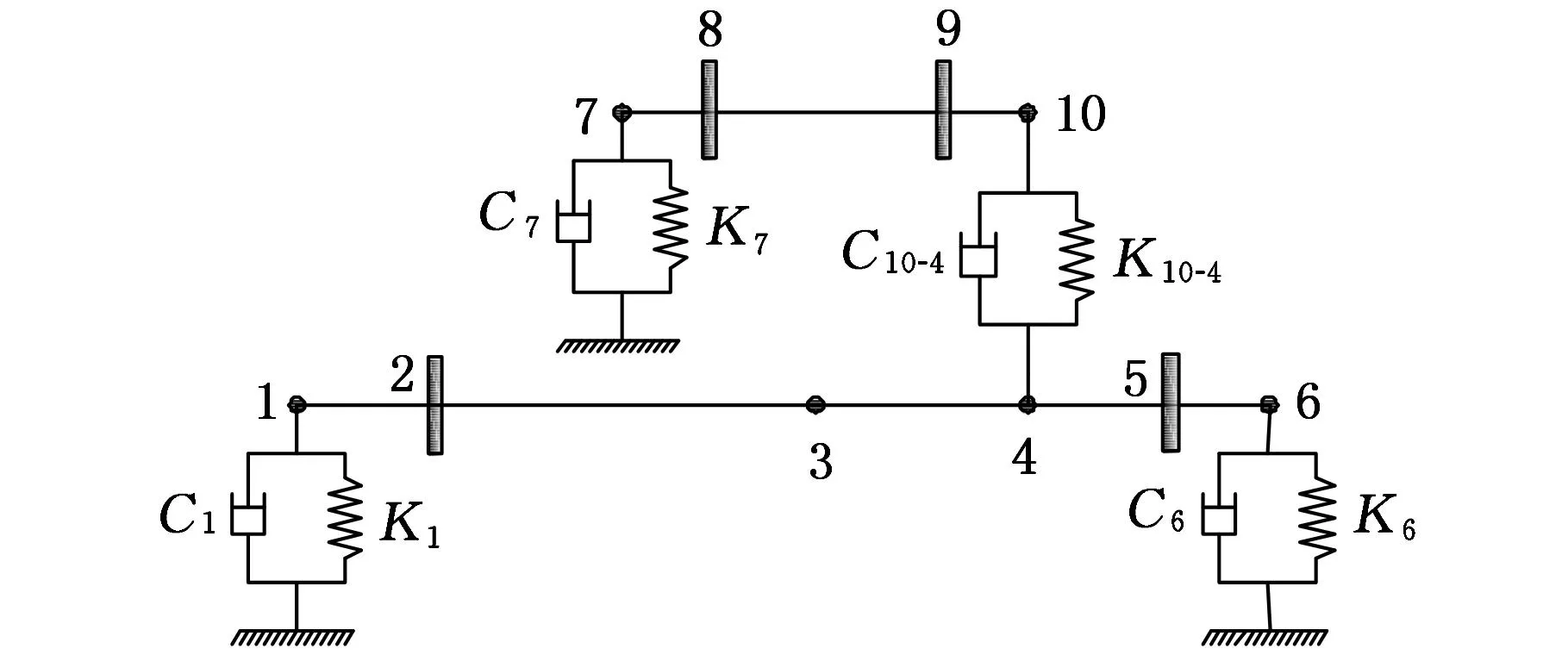
图3　单个中介轴承的双转子系统的计算模型

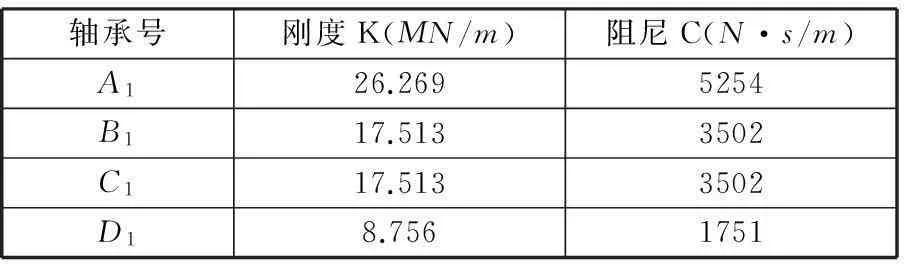
轴承号刚度K(MN/m)阻尼C(N·s/m)A126.2695254B117.5133502C117.5133502D18.7561751

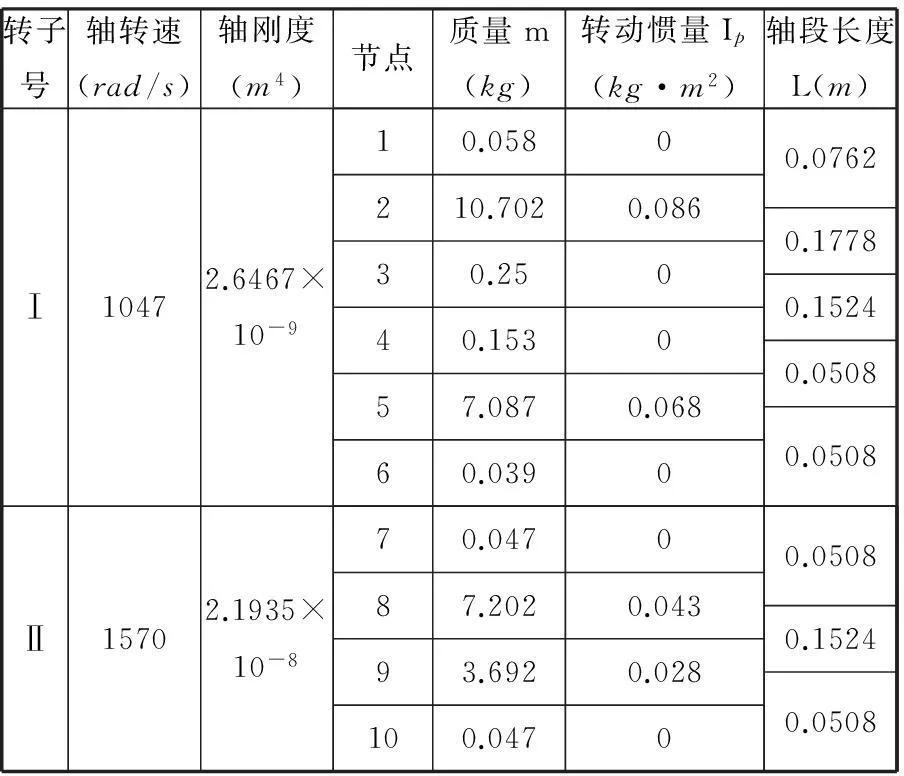
表3　模型1轴承-双转子系统的结构参数(弹性弹量E=200 GPa)

对于有阻尼的轴承-转子系统，系统的特征值计算结果是复数，其特征值可以用S=λ+iΩ表示。每一组数据都是通过MonteCarlo法模拟计算一万次得到。分析计算了耦合单元(10-4)的质量、刚度、阻尼参数各自随机变异以及同步随机变异时转子系统的随机特征值，模拟计算出的特征值的均值和标准差随变异系数的变化规律如图4～图6所示。

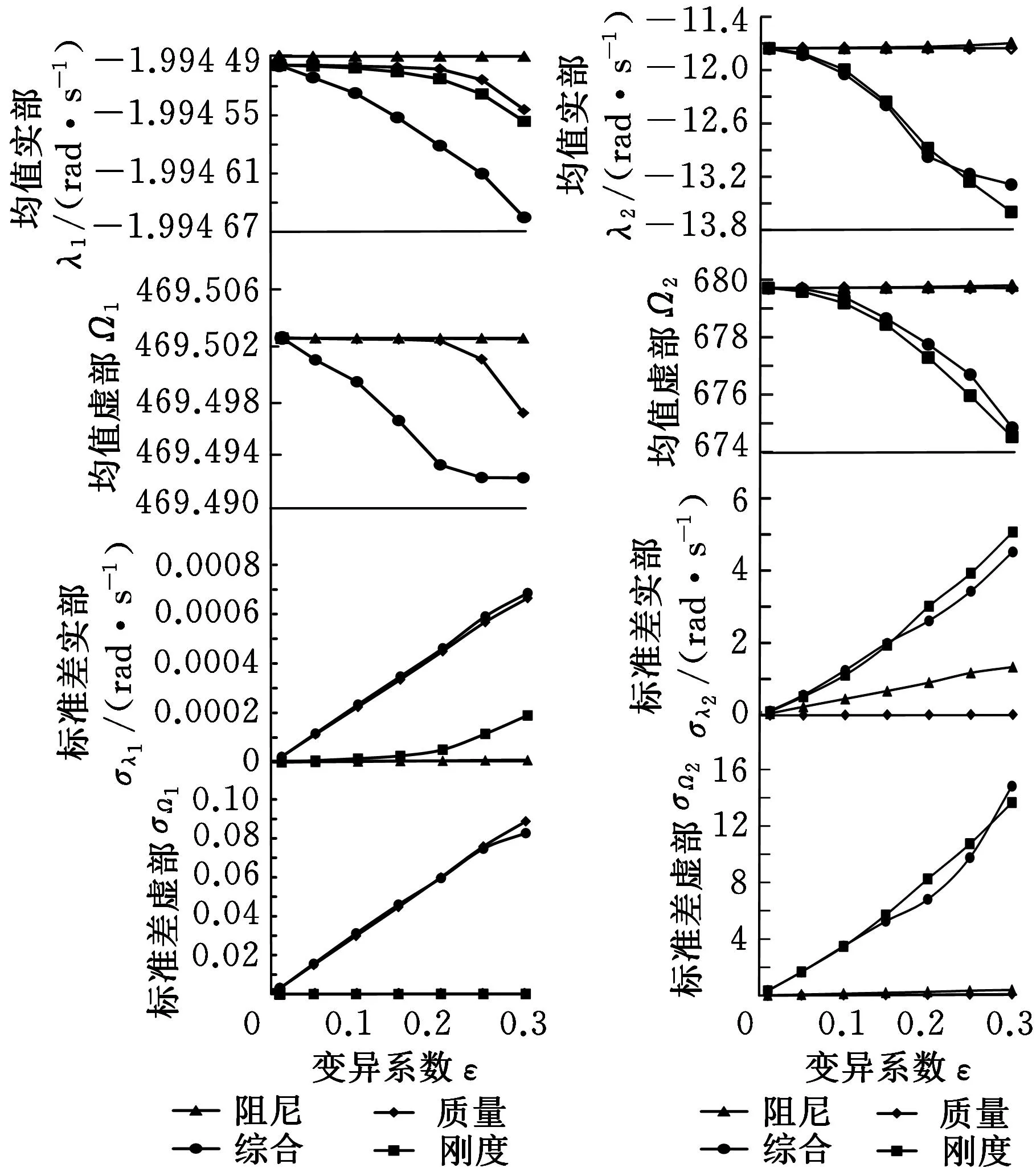
图4　　模型1一阶特征值图5　　模型1二阶特征值　均值和标准差与随机　均值和标准差与随机　参数变异系数的关系　参数变异系数的关系

图6　模型1三阶特征值均值和标准差与随机参数变异系数的关系

所求特征值的平均值是通过MonteCarlo法抽样模拟计算一万次所得到的一万个特征值的平均值。由图4可以看出：各个随机参数对系统的一阶特征值的影响都很小。而由图5、图6则可以看出：刚度参数的随机变化对二阶、三阶特征值的实部、虚部及标准差的影响都很显著，且随着变异系数的增大呈非线性变化的趋势；质量、阻尼参数的随机变化对二阶、三阶特征值的影响相对要小得多，产生这种现象的原因是由于耦合单元(10-4)的质量、阻尼参数的初值偏小，即使变异系数达到较大值，质量、阻尼的绝对值仍然不大，所以整体影响并不显著。

2.2模型2的随机特征值

模型2的计算模型如图7所示，根据整个双子系统的结构特点，将其划分为10个轴段，12个节点，各轴段的结构信息如表4所示。

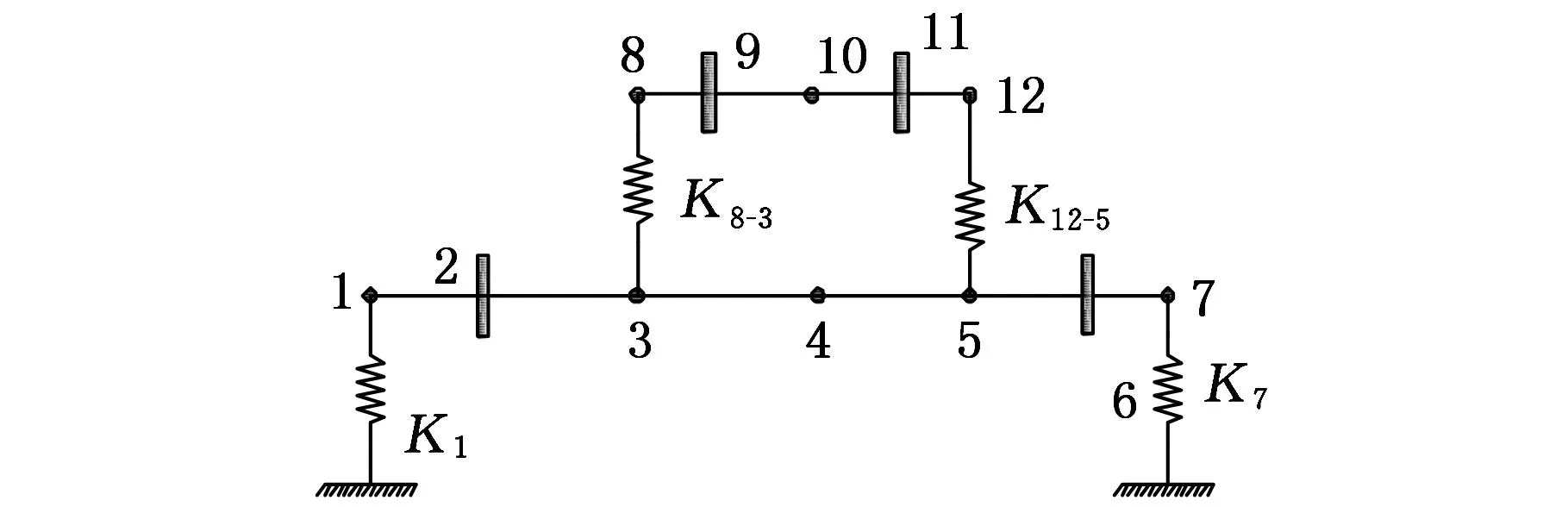
图7　两个中介轴承耦合的双转子系统的计算模型

模型2为无阻尼双转子系统，所以只考虑了两个中介轴承的质量和刚度参数随机时对双转子系统特征值的影响。从图8～图10可以得知，耦合单元(8-3)及(12-5)的质量随机时，系统的前三阶特征值都在初始特征值附近波动，特征值的变化微小。系统的质量对其特征值本应该有比较显著的影响，但分析实验结果可知，影响并不明显。分析转子系统的结构参数可知，耦合单元(8-3)及(12-5)的质量在节点3、8、5、12处，其质量初值较小，当节点处质量的变异系数较大时，其本身的变化也不大，所以对系统特征值的影响也比较小。耦合单元刚度的随机变异对系统的特征值的均值、标准差的影响都比较显著。

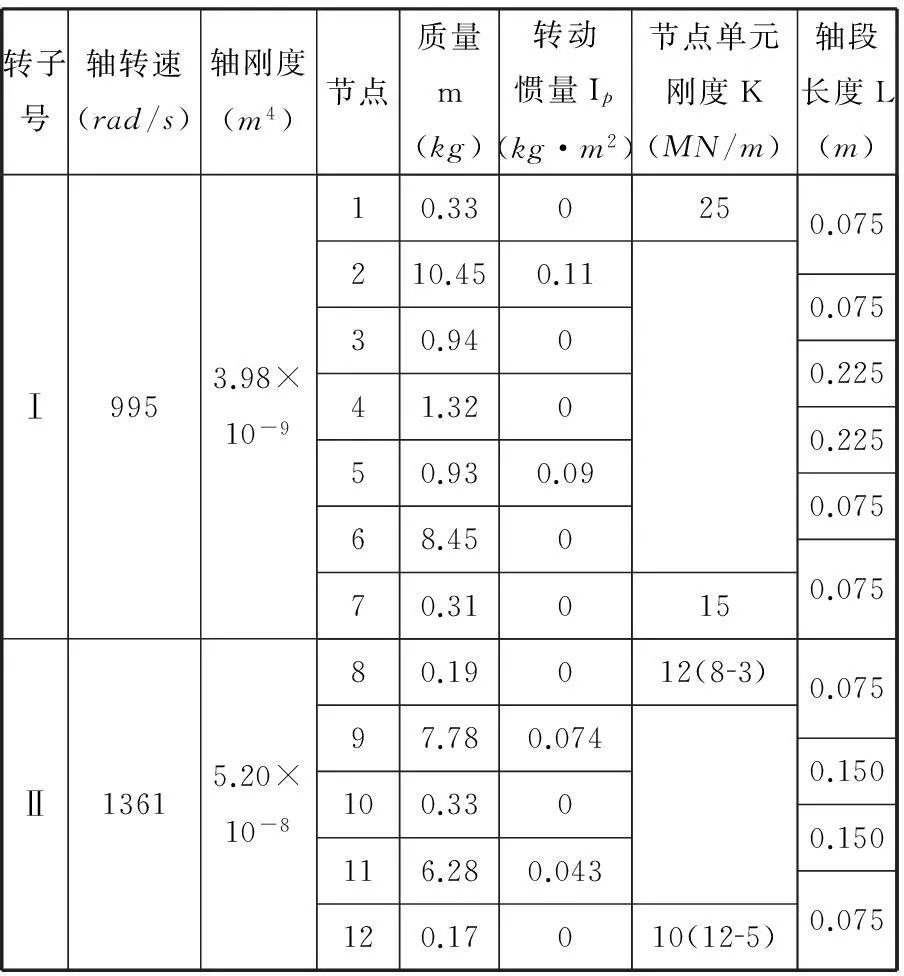
表4　模型2双转子-轴承系统的

图8　模型2一阶特征值图9　模型2二阶特征值　均值标准差与随机　标准差与随机参数　参数变异系数的关系　变异系数的关系

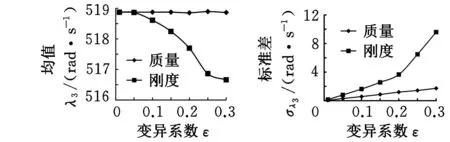
图10　模型2三阶特征值标准差与随机参数变异系数的关系

3结语

通过上述分析可知，双转子系统的中介轴承的刚度的随机性对系统的特征值的影响比较明显，特征值的均值和标准差随着刚度变异系数的增大呈非线性变化的趋势；中介轴承的质量和阻尼参数的随机性对转子系统的特征值影响较小，主要原因是它们的初值较小，即使当变异系数较大时，它们在数值上的变化也不大，所以作用不太显著。可以预期：当质量、阻尼、刚度的初值对特征值的贡献都在同样数量级别的水平时，这些参数的随机变化对特征值的均值和标准差的变化都将是明显的。

本文给出的计算方法，不仅可以分析双转子系统的中介轴承的各种参数的随机变化对转子系统特征值的影响，而且可以分析任何复杂转子系统的任何参数的随机变化对转子系统特征值的影响。

参考文献：

[1]DimentbergMF,NaessA.NonlinearVibrationsofaRotatingShaftwithBroadbandRandomVariationsofNternalDamping[J].NonlinearDynamics, 2008, 51: 199-205.

[2]DriotN,BerliozA,LamarqueCH.StabilityandTationaryResponseofaSkewJeffcottRotorwithGeometricNcertainty[J].ASMEJournalofComputationalandNonlinearDynamics, 2009, 4:1-10.

[3]魏永祥, 陈建军, 王敏娟. 随机参数齿轮-转子系统的扭转振动分析[J]. 航空动力学报, 2010，25(11): 2637-2642.

WeiYongxiang,ChenJianjun,WangMinjuan.DynamicResponseofTorsionalVibrationofGear-rotorwithRandomParameters[J].JournalofAerospacePower,2010，25(11): 2637-2642.

[4]刘保国，王威，殷学纲. 一维随机参数结构的特征值问题[J]．机械强度, 2004, 26(4): 367-370．

LiuBaoguo,WangWei,YinXuegang.EigenvalueProblemsofOneDimensionalStructurewithRandomParameters[J].JournalofMechanicalStrength, 2004, 26(4): 367-370．

[5]LiuBaoguo.EigenvalueProblemsofRotorSystemwithUncertainParameters[J].JournalofMechanicalScienceandTechnology,2012, 26(1):1-10.

[6]魏永祥，陈建军，王敏娟. 随机参数齿轮-转子系统扭转振动固有频率分析[J]. 工程力学, 2011(4): 172-177.

WeiYongxiang,ChenJianjun,WangMinjuan.NaturalFrequencyAnalysisforTorsionalVibrationofaGear-rotorSystemwithRandomParameters[J].EngineeringMechanics, 2011(4): 172-177.

[7]卢剑伟，刘梦军，陈磊，等. 随机参数下齿轮非线性动力学行为[J]. 中国机械工程,2009,20(3):330-333.

LuJianwei,LiuMengjun,ChenLei,etal.NonlinearDynamicsBehaviorofGearSystemwithStochasticParameters[J].ChinaMechanicalEngineering, 2009, 20(3): 330-333.

[8]LengXL,MengG,ZhangT,etal.BifurcationandChaosResponseofaCrackedRotorwithRandomDisturbance[J].JournalofSoundandVibration，2007，299: 621-632.

(编辑袁兴玲)

Influences of Coupling Bearing’s Random Parameters on Eigenvalues of Double Rotor System

Meng Hua1Liu Baoguo2Li Gege2

1.Shangqiu Institute of Technology,Shangqiu,He’nan,476000

2.Henan University of Technology,Zhengzhou,450007

Abstract:The stochastic problems in the eigenvalue of the complex double rotor system were analyzed by the dynamic stochastic differential equation. The eigenvalues of double rotor system was calculated with the whole transfer matrix method. After that, the relationship between the eigenvalue including its mean and standard deviation value and the random parameter’s variation coefficient was investigated with Monte-Carlo method considering the effects of random parameters such as coupling element’s mass, stiffness and damping coefficient. Meanwhile, to improve the effectiveness of this research, the conclusion was verified individually on double rotor system with one or two coupling bearings.

Key words:double rotor system; coupling bearing; random parameter; eigenvalue

作者简介：孟华，女，1988年生。商丘工学院机械工程学院助教。主要研究方向为转子动力学。刘保国，男，1962年生。河南工业大学机电工程学院教授、博士、博士研究生导师。李鸽鸽，男，1987年生。河南工业大学机电工程学院硕士研究生。

中图分类号：TH113；TH133

DOI：10.3969/j.issn.1004-132X.2016.05.020

基金项目：国家自然科学基金资助项目(11172092)

收稿日期：2015-03-15