基于闭环自适应辨识的速度环PI参数自整定

张　鹏　王文格　付　霞　聂　挺

1. 湖南大学，长沙，410082　　2. 中烟机械技术中心有限责任公司，上海，201206



基于闭环自适应辨识的速度环PI参数自整定

张鹏1王文格1付霞1聂挺2

1. 湖南大学，长沙，4100822. 中烟机械技术中心有限责任公司，上海，201206

摘要：针对永磁同步电机伺服系统速度环比例积分(PI)参数整定过程中需要反复调节、效率低等问题，提出了一种基于闭环自适应卡尔曼滤波(AKF)系统辨识的伺服系统速度环PI参数自整定方法。首先根据输入信号激励速度闭环系统，分析不同频率激励作用下闭环辨识序列的信噪比与实际输出，然后引入AKF算法辨识闭环被控对象的离散模型，最后通过遗传算法仿真搜索最优速度环PI参数。仿真与实验结果表明：该算法能有效抑制量测噪声等扰动对系统辨识精度的影响，辨识结果能够反映实际系统的动态输入输出特性，优化后的速度环具有优良的响应性能和较高的精度，便于实际工业应用。

关键词：永磁同步电机；自适应卡尔曼滤波；闭环系统辨识；遗传算法；参数自整定

0引言

在现代工业尤其是高速高精的机械系统中，永磁同步电机(PMSM)得到了广泛应用，其控制参数的好坏对交流伺服系统的动态性能有重要影响。传统的Z-N法等PID整定方法需要准确了解被控对象的模型和参数，容易陷入局部最优[1]；许多现代的智能自整定方法需要不断根据伺服系统运行时每组PI控制参数的阶跃输入响应来搜索最优参数[2]，整定时间长且电机易出故障。随着控制理论的不断发展，出现了一些采用遗传算法[3]、比例增益调节法[4]、自适应同步参数辨识法[5]、卡尔曼滤波和Elman神经网络结合法[6]等精确辨识PMSM的电阻、电感和惯量[7-8]等参数，进而整定系统比例积分(PI)控制参数的方法，但在线的高阶矩阵求逆[9]需要进行大量的实时计算，对系统硬件要求较高[10]，且一般工业系统大多是固定参数的PI控制器，因而限制了这些复杂算法的应用。

系统辨识是一种获得伺服电机系统模型进而进行参数整定的有效途径，模型的获取一般通过开环辨识[1]，但在实际中，集成化的工业对象一般不允许断开反馈做开环控制实验，且直接将开环模型应用于闭环系统也会因噪声扰动而产生偏差[11]。目前，国内外已有许多学者在闭环辨识方面进行了深入研究。文献[11]采用两阶段闭环辨识算法实现了闭环辨识，但需构造无噪声污染的中间信号。文献[12-13]在系统阶跃响应的开闭环转换上近似地求出了二阶加时滞系统传递函数。文献[14-15]分别采用最小二乘法和辅助变量法实现了对闭环系统的间接辨识，但都未针对具体的电机对象。文献[16]通过正交投影迭代法辨识了直线伺服系统位置环被控对象的高阶连续模型。文献[17]采用自适应卡尔曼滤波算法实现了对无刷直流电机的系统辨识,但对于伺服系统来说仍然是开环情况下的辨识。

相对于开环辨识，系统的闭环辨识由于会产生较大的估计误差，目前较少应用于伺服系统。本文在分析闭环辨识序列的基础上，将自适应卡尔曼滤波算法应用于PMSM的闭环系统辨识，抑制由不同工况引起的输出波动特性变化对系统辨识精度的影响，克服了直接通过伺服系统已知参数建模优化出的PI参数因驱动器和电机等内部结构不同而难以应用的问题。

1伺服系统闭环模型分析

根据某轻工机械的高速高精状况，各主要轴系均采用PMSM替代传统的齿轮传动。为保证各轴的跟随精度和相邻轴的同步精度，对各轴的PI控制参数进行整定优化。

假设空间磁场呈正弦分布，忽略铁心饱和，不计磁滞和涡流损耗的影响，PMSM为隐极式结构，并忽略齿槽转矩和其他扰动力的影响，采用id=0的矢量控制策略，则PMSM的电压方程为

(1)

式中，Ud、Uq、id、iq分别为d、q轴定子的电压与电流分量；ω为转子机械角速度；Ra、La分别为定子的电阻和等效电感。

PMSM转矩方程为

(2)

(3)

式中，Te、Tl分别为电磁转矩和负载转矩；B为黏滞摩擦因数；Pn为极对数；ψf为永磁体磁链；J为转动惯量。

根据伺服系统三环结构，电流环是内环，为保证系统稳定且带宽较大，其闭环控制系统可等效为一阶惯性环节，时间常数为Ti；速度环控制参数是伺服系统抑制波动、减少超调和振荡、提高精度的关键环节，PMSM伺服系统速度环控制结构如图1a所示。

对于图1虚线框中的模型，简化扰动部分的影响，将负载Tl及其他转矩扰动等效为系统内部的扰动。当负载一定或变化较小时，电机控制电压与转速近似为线性关系[18]，从而将虚线框中的整体近似为二阶模型进行系统闭环辨识，等效的闭环系统结构见图1b。其中，r(t)、y(t)为闭环系统的输入和输出信号，u(t)为被控对象的输入，η(t)为系统的扰动，ξ(t)为不可测噪声干扰，e(t)为误差。由此可得

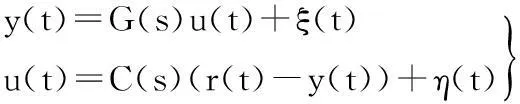
(4)

消去中间变量得

(5)

式(5)说明，不可测噪声干扰ξ(t)通过反馈环节与控制输入u(t)直接相关，导致许多算法用于闭环辨识时结果有偏[11]。进一步化简可得

(6)

(a)速度环控制结构框图

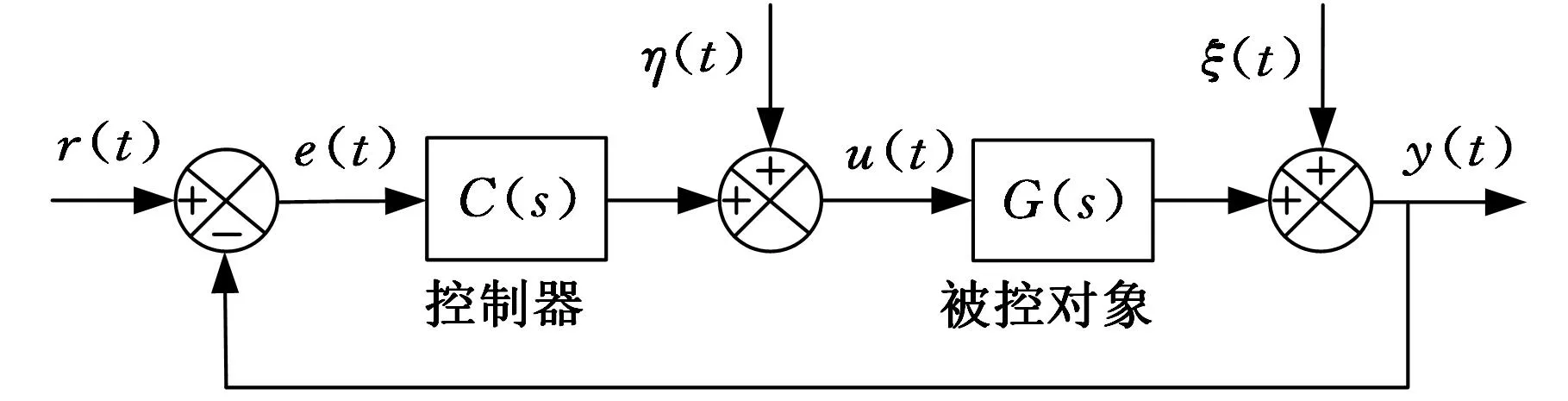
(b)闭环系统结构框图图1　速度环闭环控制结构框图

从式(5)、式(6)可以看出，当闭环系统的输入r(t)=0时，系统的扰动和不可测噪声使闭环辨识所用的输入u(t)和输出y(t)产生不同幅值的噪声干扰，且对于误差e(t)而言不可忽略。一种可行的方法是增大闭环系统的输入r(t)，并使误差e(t)以较大的速率改变，使系统的内部噪声干扰对于辨识所用的输入输出信号而言可以忽略，同时对信号进行滤波辨识。但系统的变化需要一定的时间，且受采样频率影响，对闭环系统的输入频率有一定的限制，缺少开环辨识时所需各频率成分，文献[9]也指出速度环被控对象因存在积分环节而不能直接辨识，故基于固定频率闭环辨识出的对象只是实际对象在中低频段的一种输入输出拟合。

2闭环自适应系统辨识及整定

根据图1，被控对象的传递函数为

(7)

离散化变换形式为

(8)

式中，a1、a2、b1、b2为被控对象待辨识参数。

考虑噪声干扰的影响，伺服系统速度环被控对象的差分方程模型为

ω(k)=-a1ω(k-1)-a2ω(k-2)+

b1u(k-1)+b2u(k-2)+ξ(k)

(9)

定义数据向量φ(k)=(-ω(k-1),-ω(k-2),u(k-1),u(k-2))，参数向量θ=(a1,a2,b1,b2)T，则式(9)可改写为

ω(k)=φ(k)θ+ξ(k)

(10)

式(10)是一种近似的线性关系，可看作卡尔曼滤波算法的测量方程，根据卡尔曼滤波算法可得

(11)

其中，K(k)为滤波增益矩阵，P(k)为滤波协方差矩阵，R(k)为量测噪声干扰ξ(k)的理论方差。在系统辨识中，以被估参数向量θ作为状态变量，则可得卡尔曼状态更新方程为

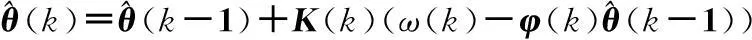
(12)

(13)

式中，m为新息的开始计算点；n为计算的长度。

m点前采用常规卡尔曼算法，为减少计算并方便工程应用，Cv(k)简写为

(14)

注意到Cv(k)即为滤波增益矩阵K(k)中元素的分母，滤波增益K(k)可改写成：

K(k)=P(k-1)φT(k)(Cv(k))-1

(15)

设定初值后，无需闭环系统速度输出波动干扰R(k)的先验知识，经过不断地递推运算，得到被控对象的模型参数θ，具体的计算循环过程依次为

(16)

采用实数编码的遗传算法对速度环PI控制参数通过仿真进行整定，这里选用偏差积分性能指标(ITAE)来计算系统的适应度函数，考虑到超调的影响，改进性能指标为

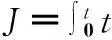
(17)

(18)

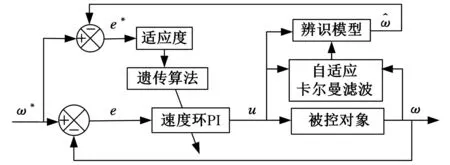
图2　遗传算法整定结构图

3仿真与实验分析

本文在西门子伺服驱动实验平台上对闭环辨识及速度环PI参数整定的有效性进行验证，硬件平台包括上位机、西门子SimotionD455控制器、西门子双轴驱动器、科尔摩根CH044A系列永磁同步电机及某轻工机械实际工况下的负载等，如图3所示。其中，上位机与控制器之间通过Ethernet总线来通信，用于数据采集和检测，控制器与驱动器之间通过DRIVE-CLIQ总线通信，编码器的反馈信号经SMC模块转换后传输到驱动器。软件系统使用SimotionScout实现信号的输入和采集，采集的数据经MATLAB/Simulink处理并优化整定出最优的速度环PI控制参数，再输入实验平台进行验证。

(a)控制柜电气系统

(b)机械系统图3　实验平台

3.1空载条件下的闭环辨识整定

首先采用一组Simotion默认的速度环PI参数：比例参数P=0.009N·m·s/rad、积分参数I=10ms，经单位换算后得到速度环PI仿真参数分别为0.000 94、0.094，实验采集被控对象的输入输出数据。为验证闭环辨识的可行性，使用不同频率的输入信号激励系统，实验结果如表1所示。

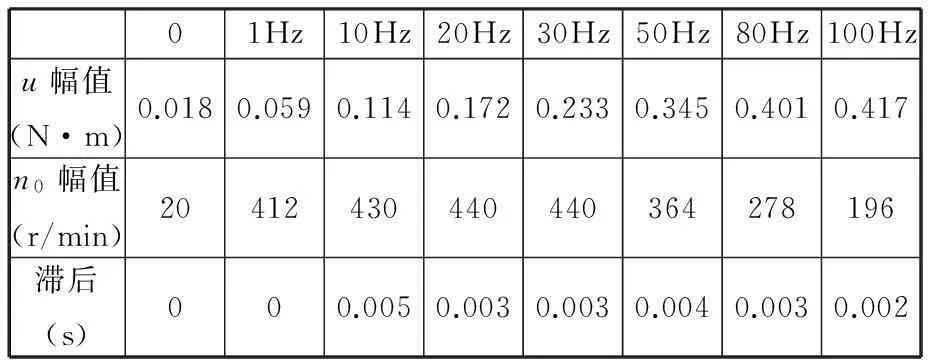
表1　幅值为400 r/min的不同频率的输入输出特性

由表1可知，当速度环无输入激励时，被控对象输入输出随机扰动的最大值分别为0.018 N·m和20 r/min；当速度环输入幅值为400的不同频率的正弦激励时，随着频率的不断增加，被控对象的输入信号幅值不断增大，输出幅值由于谐振和频率等因素影响先增大后减小，但都呈现出正弦变化规律，并叠加干扰。由图4a可知，实际系统速度环的有效频率在200 Hz以内，超出部分的伯德图因剧烈振动而不稳定，考虑辨识序列的信噪比，若采用过小的输入频率，输出转矩的幅值与无输入时的扰动最大值0.018相差不大，信号和干扰区分不明显，如表1的部分速度实际幅值输出因谐振超调而大于400 r/min的输入。图4b所示，20 Hz频段、幅值为400的正弦波辨识结果比较接近实际系统在200 Hz频段内的Bode图模型，在仿真Bode图上幅频部分在0以上，则反映表1中在50 Hz内的速度幅值超调，而实验Bode图因采用随机信号测得而未表现出来。频率太小未能充分激励系统，太大则受采样频率限制，均恶化辨识结果，减小带宽。

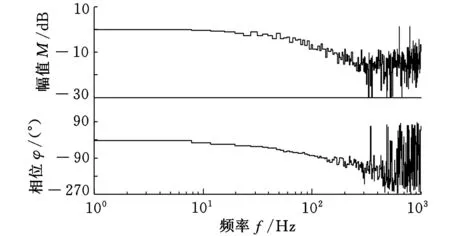
(a)伺服系统速度闭环实验Bode图

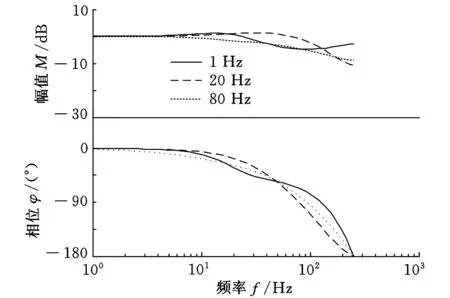
(b)辨识结果速度闭环仿真Bode图图4　速度闭环Bode图

为了体现自适应卡尔曼滤波(AKF)算法抑制噪声干扰的有效性，在相同的实验数据条件下与工程中广泛采用的因能避免数据饱和而用于参数在线实时估计的递推最小二乘法(RLS)相比较，其辨识结果和辨识误差如图5所示，可见在电机未运行而处于噪声扰动时，RLS算法的辨识结果受系统扰动影响较大，辨识参数不断波动，AKF算法因带有噪声滤波而不受系统扰动的影响，辨识参数皆为零，且辨识最大误差较最小二乘法减小了50%。AKF算法辨识得到的离散系统模型为

(a)AKF与RLS算法辨识结果

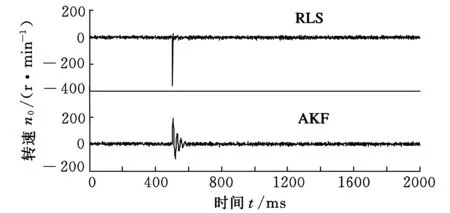
(b)AKF与RLS算法辨识误差图5　空载条件AKF与RLS算法辨识结果与误差

设定遗传算法速度环PI参数整定范围分别为(0，0.09]和(0，100]，通过幅值为400的阶跃响应仿真搜索得到最优PI参数为：P=0.0105 N·m·s/rad，I=21.526 ms，整定前后仿真及实验结果如图6所示。

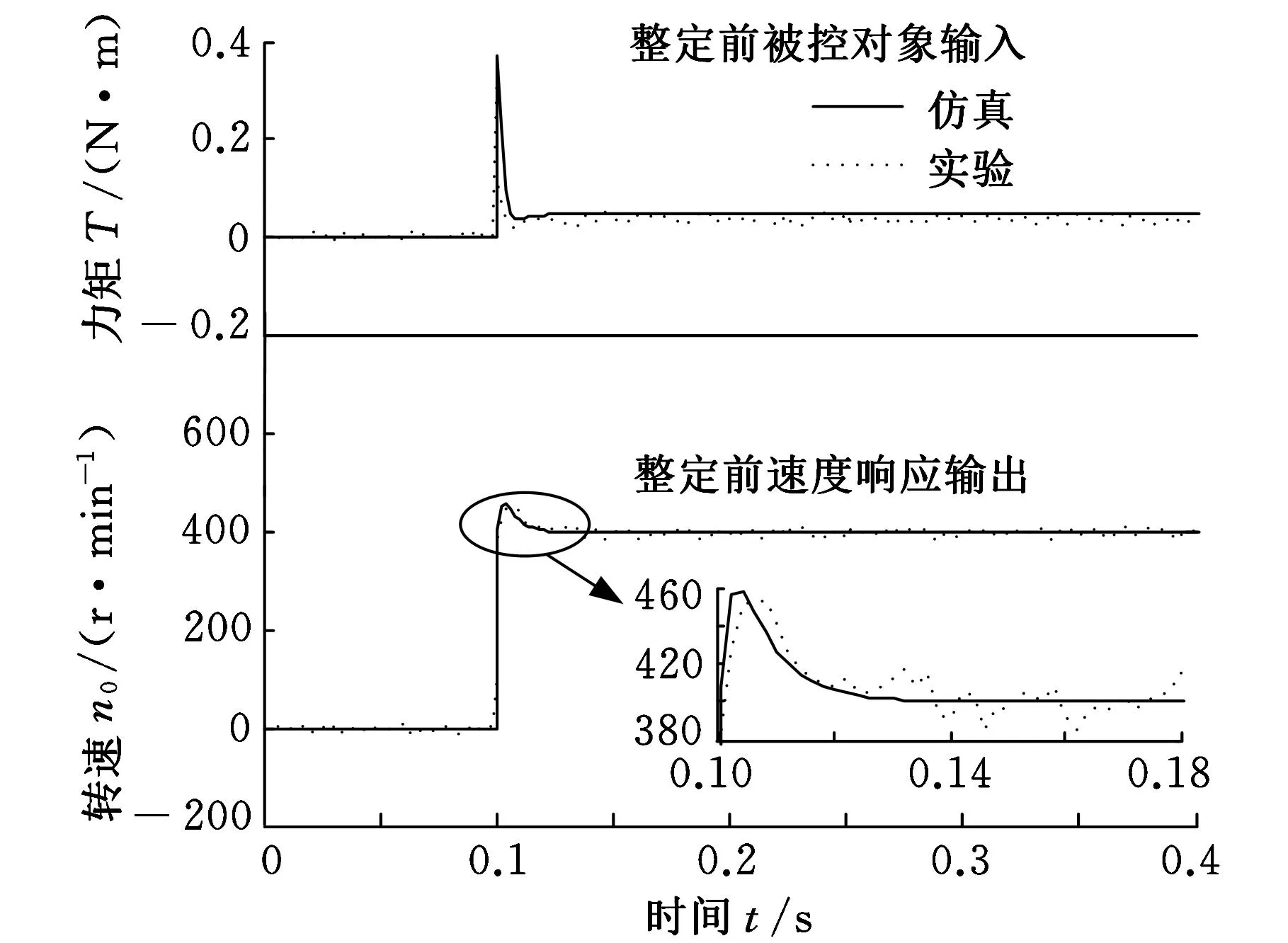
(a)整定前

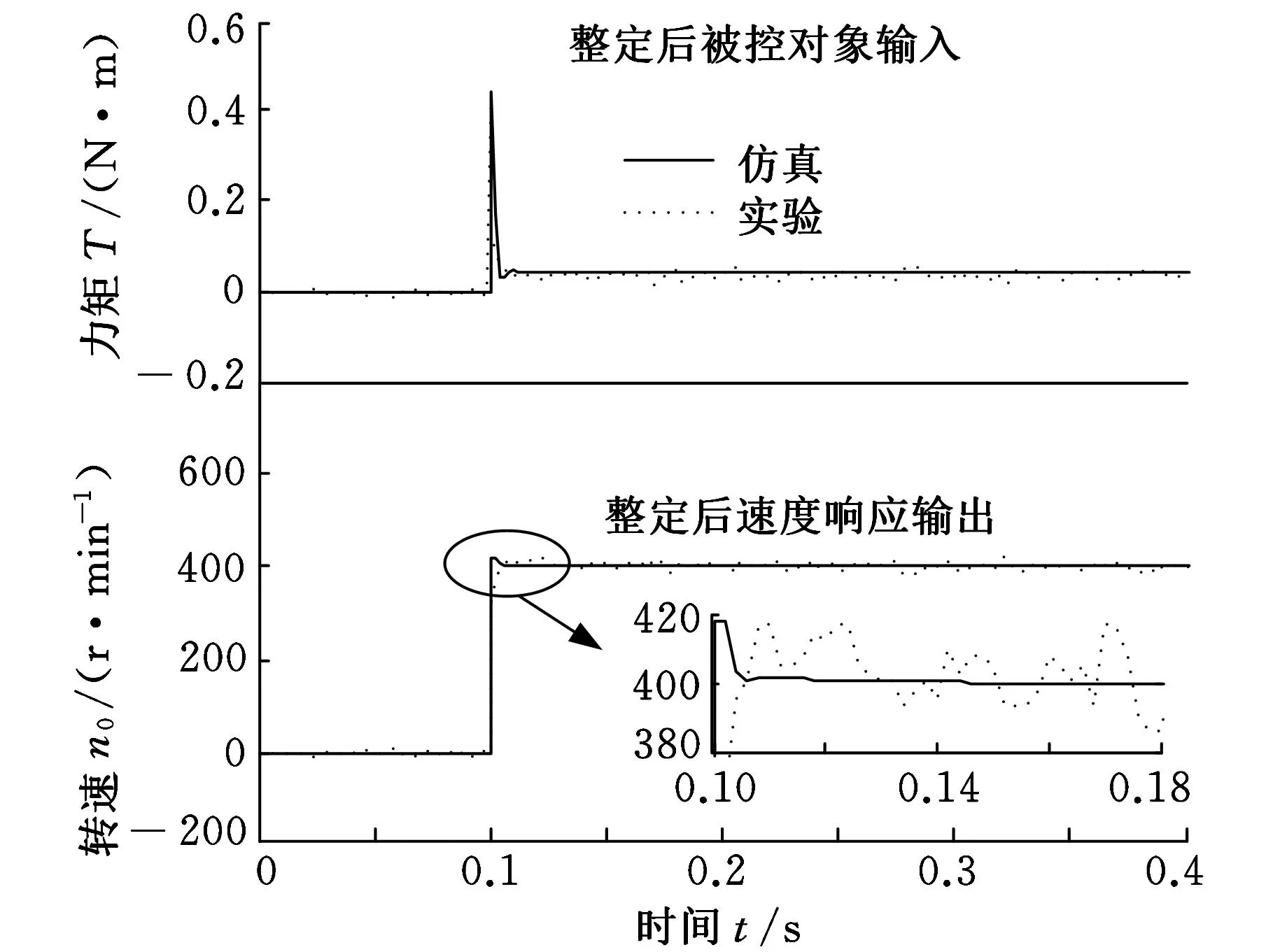
(b)整定后图6　空载整定前后的输入输出

图6说明，电机在0.1 s内未运行和稳定时的闭环速度输出扰动幅值均为±20 r/min，AKF算法辨识的被控对象离散模型经仿真能够较好地拟合实际伺服系统速度环的动态输入输出特性，整定前速度环超调约为54 r/min，整定后超调约为20 r/min，与空载无激励情况下系统的扰动幅值相同。

3.2实际负载下的闭环辨识整定

为进一步验证AKF辨识算法在实际工程应用中的可行性，实验采集了轻工机械在实际负载工况运行过程中被控对象的输入输出数据。由于实际工况的限制，实际过程中速度环PI控制器的输出转矩有限幅，且伺服系统的正弦运行频率一般不会很高，经反复实验采用0.25 Hz幅值为400的正弦波辨识，其速度环PI的最大输出转矩接近限幅。实验所用的速度环PI参数为Simotion提供的一组参考数据：P=10 N·m·s/rad，I=30 ms，速度环PI控制器的转矩输出限幅为±13.9026 N·m，速度闭环系统的辨识结果如图7所示。

(a)辨识参数a1(b)辨识参数a2

(c)辨识参数b1(d)辨识参数b2图7　实际负载下AKF与RLS算法辨识结果

由图7可知，与空载情形相似，RLS算法在伺服系统未运行而处于系统噪声扰动时辨识结果上下波动较大。此外，电机运行时RLS算法辨识结果有一定的波动，而AKF算法通过滤波过程使辨识的结果较平滑。电机在实际负载运行条件下AKF算法的辨识结果为

遗传算法速度环PI参数的范围分别设定为(0，100]和(0，200]，通过仿真搜索得到最优PI参数为P=24.851N·m·s/rad，I=26.614ms，实际负载条件下整定前后的仿真及实验结果如图8所示。

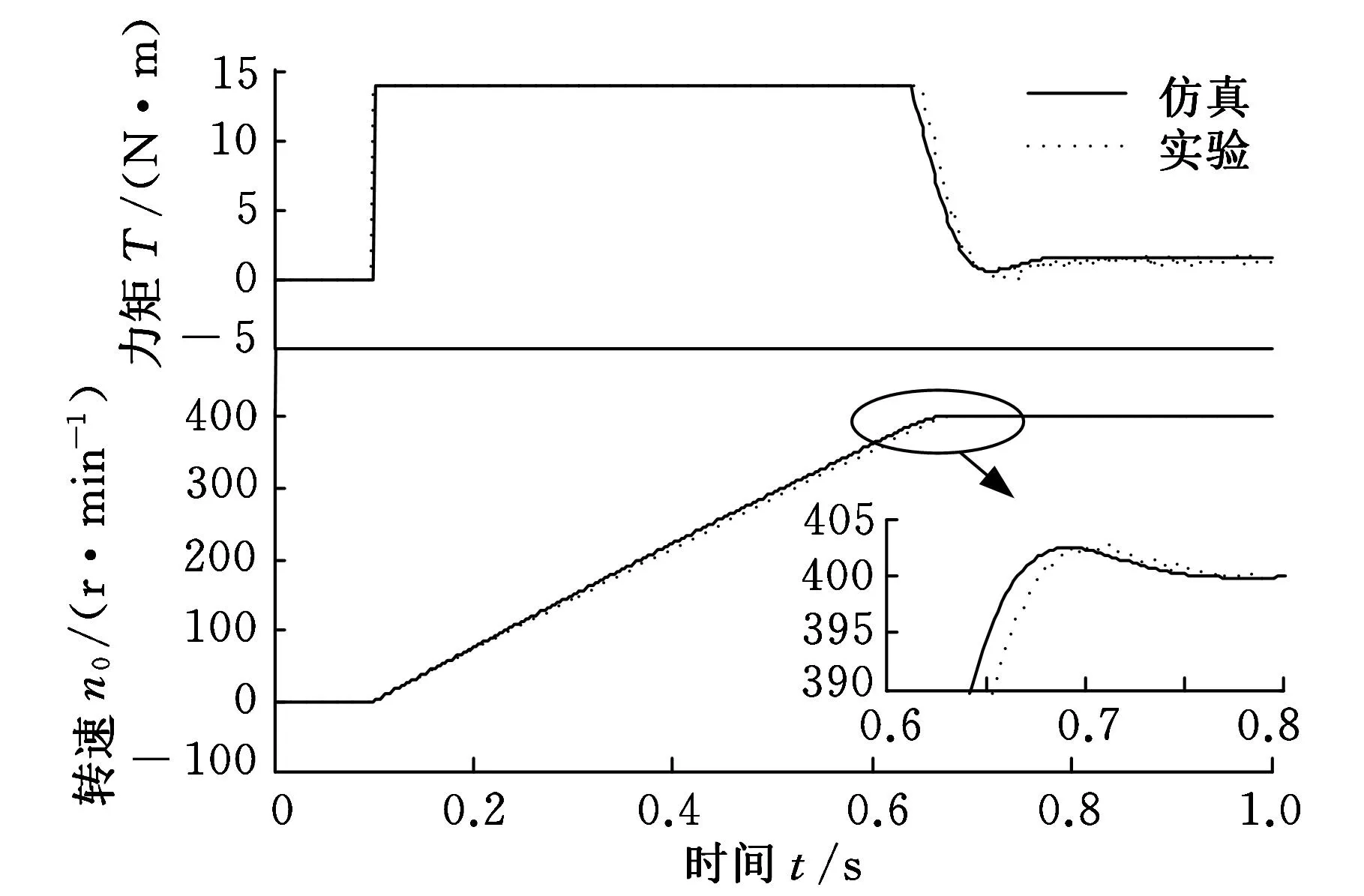
(a)整定前

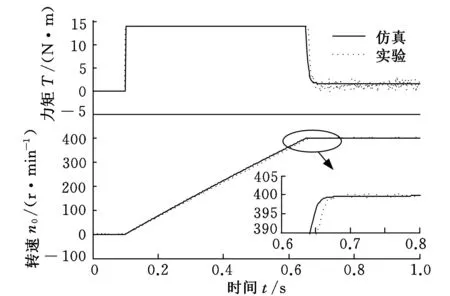
(b)整定后图8　实际负载整定前后输入(力矩)与输出(转速)

通过图8可以看出，实际系统闭环辨识的离散模型经仿真能够较好地拟合速度环实际系统的动态输入输出特性，但由于辨识模型的微小误差，仿真曲线在最大转矩输出的速度上升阶段存在较小的超前时间累积。电机在0.1 s内未运行时速度噪声扰动幅值为0.01 r/min，速度环PI的电磁输出转矩在稳态时约为1.5 N·m，整定前后速度稳态误差皆在±0.6 r/min以内，整定前电机超调约3 r/min，达到稳态时间约0.77 s，整定后超调约为0.6 r/min且响应较快，达到稳态时间约为0.72 s，整定后的伺服系统速度环性能得到了较大提高。

4结论

(1) 本文提出了一种新型实用的PMSM伺服系统速度环PI控制参数自整定方法，该方法针对伺服系统速度环的闭环模型，无需闭环系统速度输出的噪声扰动特性先验知识和具体的伺服系统参数数值，通过闭环被控对象的辨识来仿真整定速度环PI参数，避免了在线整定过程中的反复调节和参数切换冲击等问题。

(2)该自适应滤波辨识算法受不同负载和系统噪声扰动的影响较小，辨识结果在中低频段能较理想地拟合实际系统的动态输入输出特性，在仿真基础上的速度环PI参数整定能够有效地提高伺服系统的动态性能，减小超调量，便于在直接采用控制器驱动器的工业伺服系统中应用。

参考文献：

[1]郑世祺，唐小琦，卢少武,等．PMSM伺服系统参数自整定研究[J]．电气传动，2013，43(3)：10-13．

Zheng Shiqi, Tang Xiaoqi, Lu Shaowu, et al. Study on Parameters Auto-tuning of Servo System of PMSM[J]. Electric Drive, 2013, 43(3): 10-13.

[2]肖启明，杨明，刘可述,等．PMSM伺服系统速度环PI控制器参数自整定及优化[J]．电机与控制学报，2014，18(2)：102-107．

Xiao Qiming, Yang Ming, Liu Keshu, et al. Parameters Self-tuning and Optimization of Speed PI Controller for PMSM Servo System[J]. Electric Machines and Control, 2014, 18(2): 102-107.

[3]Fung Rong-Fong，Hsu Yi-Lung，Huang Ming-Shyan．System Identification of a Dual-stage XY Precision Positioning Table[J]．Precision Engineering，2009，33(1)：71-88．

[4]Lee Seok-Beom．Closed-loop Estimation of Permanent Magnet Synchronous Motor Parameters by PI Controller Gain Tuning[J]．IEEE Transactions on Energy Conversion，2006，21(4)：863-870．

[5]Liu L，Cartes D A．Synchronisation Based Adaptive Parameter Identification for Permanent Magnet Synchronous Motors[J]．IET Control Theory，2007，1(4)：1015-1022．

[6]Wang Song，Shi Shuangshuang，Chen Chao,el al．Identification of PMSM Based on EKF and Elman Neural Network[C]//Proceeding of the IEEE International Conference on Automation and Logistics. Shenyang，2009:1459-1463．

[7]梁骄雁，胡育文，鲁文其．永磁交流伺服系统的抗扰动自适应控制[J]．电工技术学报，2011，26(10)：174-180．

Liang Jiaoyan, Hu Yuweng, Lu Wenqi. Anti-disturbance Adaptive Control of Permanent Magnet AC Servo System[J]. Transactions of China Electrotechnical Society, 2011, 26(10): 174-180.

[8]鲁文其，胡育文，梁骄雁,等．永磁同步电机伺服系统抗扰动自适应控制[J]．中国电机工程学报，2011，31(3)：75-81．

Lu Wenqi, Hu Yuwen, Liang Jiaoyan, et al. Anti-disturbance Adaptive Control for Permanent Magnet Synchronous Motor Servo System[J]. Proceeding of the CSEE, 2011, 31(3): 75-81.

[9]李长红，陈明俊，杨燕,等．永磁同步电机的相关辨识法自整定速度控制[J]．中国电机工程学报，2014，34(30)：5360-5367．

Li Changhong, Chen Mingjun, Yang Yan, et al. A Correlation Identification Based Auto-Tuning Speed Control Method for Permanent Magnet Synchronous Motor Drives[J]. Proceeding of the CSEE, 2014, 34(30): 5360-5367.

[10]崔业兵，郑健，鞠玉涛,等．舵机永磁无刷直流电机控制器参数离线整定[J]．电工技术学报，2013，28(9)：281-287．

Cui Yebing, Zheng Jian, Ju Yutao, et al. Off-line Controller Parameters Tuning for Electromechanical Actuator Systems with Permanent Magnet Brushless DC Motor Driving[J]. Transactions of China Electrotechnical Society, 2013, 28(9): 281-287.

[11]莫建林，王伟，许晓鸣,等．系统辨识中的闭环问题[J]．控制理论与应用，2002，19(1)：9-14．

Mo Jianlin, Wang Wei, Xu Xiaoming, et al. Closed-loop Problem in System Identification[J]. Control Theory and Applications, 2002, 19(1): 9-14.

[12]李大字，曾繁友，靳其兵．基于阶跃响应和开闭环转换的三步法辨识[J]．仪器仪表学报，2009，30(6)：30-33．

Li Dazi, Zeng Fanyou, Jin Qibing, et al. A Three-step Closed-loop Identification Method Based on Step Response and Open Loop Transformation[J]. Chinese Journal of Scientific Instrument, 2009, 30(6): 30-33.

[13]朱学峰，肖术骏，王秀．一种新的实用PI控制闭环辨识方法[J]．控制理论与应用，2010，27(9)：1240-1244．

Zhu Xuefeng, Xiao Shujun, Wang Xiu. A New Practical Method for Closed-loop Identification with PI Control[J]. Control Theory and Applications, 2010, 27(9): 1240-1244.

[14]Zheng Weixing．Parametric Identification of Linear Systems Operating under Feedback Control[J]．IEEE Transactions on Circuits and Systems—I: Fundamental Theory and Applications，2001，48(4)：451-458．

[15]Zheng Weixing．On Indirect Identification of Feedback-control Systems Via the Instrumental Variables Methods[J]．IEEE Transactions on Circuits and Systems—I: Fundamental Theory and Applications，2003，50(9)：1232-1238．

[16]杨亮亮，武晓虎，史伟民,等．基于正交投影迭代学习的高频响闭环运动控制系统模型参数辨识研究[J]．机械工程学报，2015，51(1)：188-195．

Yang Liangliang, Wu Xiaohu, Shi Weimin, et al. Research on Model Parameters Identification of Closed-loop High Frequency Motion Control System Based on Iterative Learning of Orthogonal Projection[J]. Journal of Mechanical Engineering, 2015, 51(1): 188-195.

[17]魏彤，郭蕊．自适应卡尔曼滤波在无刷直流电机系统辨识中的应用[J]．光学精密工程，2012，20(10)：2308-2314．

Wei Tong, Guo Rui. Application of Adaptive Kalman Filtering to System Identification of Brushless DC Motor[J]. Optics and Precision Engineering, 2012, 20(10): 2308-2314.

[18]贾永峰，谷立臣．模型与条件PID补偿的永磁伺服电动机驱动液压源流量控制[J]．机械工程学报，2014，50(8)：197-204．

Jia Yongfeng, Gu Lichen. Model and Conditional PID Compensation Control on Flow of Hydraulic Source Drive by Permanent Magnet Servo Motor[J]. Journal of Mechanical Engineering, 2014, 50(8): 197-204.

[19]卞鸿巍，金志华，王俊璞,等．组合导航系统新息自适应卡尔曼滤波算法[J]．上海交通大学学报，2006，40(6)：1000-1003．

Bian Hongwei, Jin Zhihua, Wang Junpu, et al. The Innovation Based Estimation Adaptive Kalman Filter Algorithm for INS/GPS Integrated Navigation System[J]. Journal of Shanghai Jiaotong University, 2006, 40(6): 1000-1003.

[20]杨长林，柏秀亮，刘廷飞,等．新息自适应区间Kalman滤波算法及其应用[J]．传感器与微系统，2012，31(11)：132-135．

Yang Changlin, Bai Xiuliang, Liu Yanfei, et al. Innovation-based Adaptive Interval Kalman Filtering Algorithm and Its Application[J]. Transducer and Microsystem Technologies, 2012, 31(11): 132-135.

(编辑袁兴玲)

Speed PI Parameter Auto-tuning Based on Closed-loop Adaptive Identification

Zhang Peng1Wang Wenge1Fu Xia1Nie Ting2

1.Hunan University，Changsha，410082

2.Tobacco Machinery Co., Ltd. Technology Center，Shanghai，201206

Abstract：In order to solve the problems of speed PI parameter tuning process needed to be adjusted repeatedly or had low efficiency for PMSM servo system, a practical method of speed PI parameter auto-tuning was proposed based on the closed-loop AKF system identification. Though speed closed-loop input excitation, the signal-to-noise ratio and actual output of closed-loop identification sequence under different frequencies were analyzed, then the discrete model of closed-loop controlled objects was identified by AKF algorithm, and finally by genetic algorithm the optimal speed PI parameters were searched through simulation. Simulation and experimental results show that the presented algorithm can effectively suppress the influences of the measurement noise disturbances on system identification accuracy, and the recognition result can reflect the dynamic input-output characteristics of the actual system, moreover, excellent response and high accuracy have appeared after speed optimization and it is convenient to the practical industrial applications.

Key words：permanent magnet synchronous motor(PMSM); adaptive Kalman filter(AKF); closed-loop system identification; genetic algorithm; parameter auto-tuning

作者简介：张鹏，男，1989年生。湖南大学机械与运载工程学院硕士研究生。主要研究方向为机电一体化、伺服系统控制与仿真。王文格，男，1966年生。湖南大学机械与运载工程学院教授。付霞，女，1989年生。湖南大学机械与运载工程学院硕士研究生。聂挺，男，1987年生。中烟机械技术中心有限责任公司工程师。

中图分类号：TM351;TP273

DOI：10.3969/j.issn.1004-132X.2016.05.012

基金项目：国家自然科学基金资助项目(51075137)

收稿日期：2015-03-23