基于能量函数的永磁同步电机无速度传感器H∞控制

吴忠强　吴昌韩　贾文静　赵立儒

燕山大学，秦皇岛， 066004



基于能量函数的永磁同步电机无速度传感器H∞控制

吴忠强吴昌韩贾文静赵立儒

燕山大学，秦皇岛， 066004

摘要：研究了基于能量函数的永磁同步电机无速度传感器H∞控制问题。为有效控制电机转速，首先对无扰动条件下的永磁同步电机哈密顿模型进行整形，使转速达到期望值。然后，在存在扰动的条件下，设计了一种基于哈密顿函数的H∞控制器。最后，采用基于哈密顿函数的扩张+反馈方法设计了一种观测器，对转子角速度进行测量，实现了无速度传感器整形+H∞控制。仿真结果表明，基于观测器的整形+H∞控制器能实现对角速度的高精度估计，可有效克服扰动，并较好地实现了对电机转速的控制功能。

关键词：能量函数；永磁同步电机；无速度传感器；H∞控制

0引言

永磁同步电机(permanent magnet synchro-nous motors, PMSM)系统是一种典型的多变量、强耦合非线性系统，具有复杂的动态行为，在一定的参数条件下会产生如混沌、Hopf分岔、周期振荡等复杂运动，使其转速或转矩出现剧烈振荡[1]。在需要电机稳定运行或精准调速的场合，上述现象的存在将引起系统不稳定，直接影响电机的动态性能。

随着对电机小型化、微型化的需求日益增加，同时考虑到设备故障率、成本等问题，无速度传感器控制方案逐渐成为研究热点[2-5]。文献[6]针对永磁同步电动机，设计了由积分反步控制和滑模变结构模型参考自适应速度辨识器组成的无速度传感器矢量控制系统；文献[7]在永磁同步电机无速度传感器控制系统中，为提高系统的鲁棒性和自适应能力，给出了一种基于模糊控制原理的改进型自抗扰控制算法；文献[8]针对永磁同步电机，提出了一种基于新的高速滑模观测器的无速度传感器控制策略；文献[9]为减小速度检测对无轴承感应电动机系统稳定性与精度的影响，提出了一种基于人工神经网络反演法的无速度传感器矢量控制方案。

能量函数简单、直观，物理意义易于理解，在电机控制领域得到广泛应用。哈密顿(Hamilton)函数是一种典型的能量函数，是非线性科学中一个重要的研究方向。哈密顿函数、能量流以及系统矩阵所反映的系统内部关联机制能为研究者提供研究对象更多的动力学细节[10]。针对典型的永磁同步电机非线性系统，哈密顿系统理论提供了更多的可行性方法。文献[11]针对高性能的表面式永磁同步电机调速系统,推导出考虑逆变器的统一端口受控耗散哈密顿数学模型，设计了驱动系统的无源控制器；文献[12]基于哈密顿系统并充分利用系统物理结构和无需补偿“无功力”的优点，建立了混沌系统的哈密顿模型，并考虑了系统存在外扰情况下的H∞控制方法；文献[13]针对电动汽车用永磁同步电机，利用互联和阻尼配置及能量整形方法实现了考虑铁损的永磁同步电机驱动系统的哈密顿镇定控制。

本文研究了基于能量函数的永磁同步电机无速度传感器H∞控制问题。为有效控制电机转速，对无扰动状态下的永磁同步电机进行整形，通过互联与阻尼配置的方法，使电机转速达到期望值，同时永磁同步电机哈密顿系统在期望平衡点达到最小值，满足后续设计需要。考虑扰动存在的情况下，设计了一种H∞控制器来实现对扰动的抑制。采用基于哈密顿函数的扩张+反馈方法设计了一种观测器，对转子角速度进行测量。仿真结果表明，基于观测器的整形+H∞控制器能有效克服电压波动对电机转速的影响，实现对电机的转速控制功能。

1永磁同步电机模型

通过Clarke-Park变换，永磁同步电机系统动态模型可表示为

(1)

Te=Pψiq+P(Ld-Lq)idiq

式中，u、i、L分别为电压、电流、电感；下标d、q分别表示d、q轴分量，对于表面式永磁同步电机，Ld=Lq；Rs为定子电阻，下标s表示定子；ω为转子角频率；P为极对数；J为驱动系统的转动惯量；B为黏滞系数； TL为负载转矩；Te为电磁转矩；ψ为永磁体产生的励磁磁链。

2PMSM系统的端口受控哈密顿(PCH)模型的建立

以表面式永磁同步电机为例。定义系统状态向量x、控制输入向量u分别为

其中，D=diag(L,L,J)。令

T=[00-TL]T

并取永磁同步电机系统的哈密顿函数为其电能与机械能之和，即

(2)

可知

∂xH=[idiqω]T

存在扰动情况下，式(1)所示的永磁同步电机动态模型可以表示成如下的端口受控哈密顿系统：

(3)

其中，输出y∈R2；g11，g22为常数；ξ为未知扰动信号；J(x)为反对称矩阵，反映了系统内部的互联结构；R(x)为正定对称矩阵，反映了端口上的附加阻性结构。

令u=u1+u2+u3，其中，u1为待设计的整形控制器，其目的是实现转速跟踪，u2为考虑扰动状态下的H∞控制器，u3为扩张+反馈法设计观测器时的控制器，下面分别进行设计。

3整形控制器设计

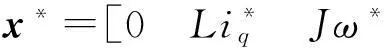
根据端口受控哈密顿系统设计要求，系统的能量函数需要在期望的平衡点x*处取得极小值。若不为极小值，则需要对系统能量函数进行整形。显然系统式(3)的能量函数式(2)在期望的平衡点处不为极小值(∂xH(x*)≠0)，需要对系统能量函数进行整形。

选取期望的哈密顿函数为

令

(4)

(5)

Ha(x)=Hd(x)-H(x)

[Jd(x)-Rd(x)]∂xHa=

-[Ja(x)-Ra(x)]∂xH+g(x)u1+T

(6)

(7)

(8)

(9)

将u1代入式(3)，系统式(3)可整形为

(10)

4H∞控制器设计

考虑ξ≠0的情况下H∞控制器u2的设计。令u3=0，则整形后的系统可表示为

(11)

系统式(11)的H∞控制问题可描述为：对于给定的干扰抑制水平γ≥0，需求得状态反馈律u2，使得闭环系统的L2增益(由ξ到y)不大于γ，即

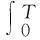
(12)

成立。

引理1[14]针对系统

(13)

f(x)、h(x)为非线性函数，若存在函数V(x)≥0(V(x*)=0)，使得哈密顿-雅可比不等式

(14)

成立，则系统的L2增益(由ξ到y)不大于γ，即式(12)成立。

H∞控制器u2的设计以定理形式给出如下。

定理1若系统式(11)满足

(15)

则系统式(11)的H∞控制问题可由下列控制律完成：

(16)

证明：

将式(16)代入式(11)，可得

(17)

令

h(x)=gT(x)∂xHd

(18)

(19)

则式(17)可表示成式(13)形式。

取V(x)=Hd(x)+c≥0，其中c=-Hd(x*)，则由式(15)和式(17)可得

g(x)gT(x))∂xHd=-(∂xHd)T[Rd(x)+

(20)

由引理1可知，系统式(11)的L2增益(由ξ到y)不大于γ。

5观测器设计

考虑小型化和节约成本，不对电机角速度进行直接测量，采用观测器进行观测。以观测量代替控制器式(7)、式(8)、式(16)中的不可测量。令ξ=0，u2=0，系统式(10)可改写为

(21)

作如下假设：

假设1存在非零矩阵K(x)，使得函数矩阵

W(x)=Rd(x)+(g(x)K(x)+KT(x)g(x))≥0

(22)

成立。

所设计的观测器为

(23)

证明：

由式(21)、式(23)可组成如下扩展系统：

(24)

(25)

将式(25)代入式(24)，可得

(26)

由假设1可知

(27)

可知系统式(26)是稳定的。

系统式(3)基于观测器的整形+H∞转速控制器为

(28)

(29)

6仿真分析

以一台表面式永磁同步电机为例，其参数为：Rs=0.029 Ω，L=11.5 mH，J=1.191×10-3kg·m2，B=0.0162 N·m·s/rad，P=2，ψ=0.034 N·m/A。

图1　电机转子角速度实际值和观测值

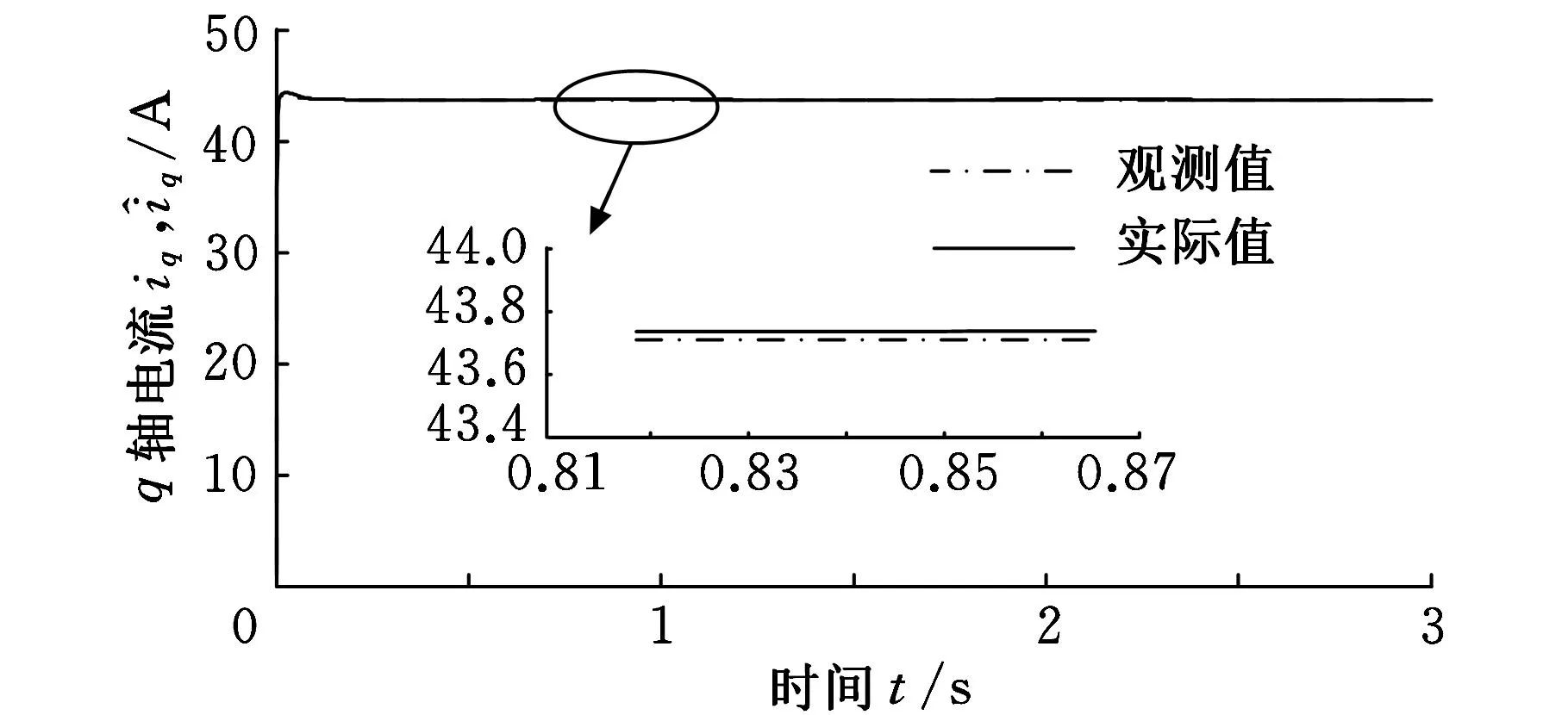
图2　q轴电流实际值和观测值

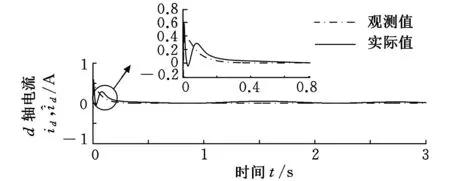
图3　d轴电流实际值和观测值

从图1～图3可看出，观测器较好地估计出电机三个状态量的实际值，调整过程快，估计精度高。基于观测器的整形+H∞控制器不但将电机转速控制在期望值，且扰动抑制效果明显。

利用CCS3.3软件来观察永磁同步电机实际转速和估计转速，将实际转速存入DLOG_4CH_buff3寄存器中，估计转速存入DLOG_4CH_buff4寄存器中，寄存器容量为1024。选择View→Graph→Time/Frequency，CCS3.3弹出如图4所示的图形对话框，利用此图形可实时观测电机速度，图中两个坐标(589,0.382 874)和(589,0.382 874)分别代表寄存器第589个值对应的电机实际转速和估计转速。0.382 874是与60 rad/s相对应的标幺值。从图4中可看出，此刻转速估计得很好，有些时刻有微小偏差，与仿真结果相符。说明所设计观测器和控制器是正确的。

图4　转子角速度实际值和观测值实验曲线

7结束语

研究了基于能量函数的永磁同步电机无速度传感器H∞控制问题。为将电机转速控制至期望值，基于互联与阻尼参数配置方法，对无扰动状态下的永磁同步电机模型进行整形控制，使电机转速达到期望值。在存在扰动的状态下，设计了一种H∞控制器。采用基于哈密顿函数的扩张+反馈方法设计了一种观测器，对转子角速度进行测量。仿真结果表明，观测器能较好地对电机状态进行估计，同时基于观测器的整形+H∞控制器既能有效克服电压波动对电机转速的影响，又能实现对电机转速的高精度跟踪。

参考文献：

[1]Krishnan R, Bharadwaj A S. A Review of Parameter Sensitivity and Adaptation in Indirect Vector Controlled Induction Motor Drive Systems[J]. IEEE Transactions on Power Electronics, 1991, 6(4): 695-703.

[2]张兴,郭磊磊,杨淑英,等.永磁同步发电机无速度传感器控制[J].中国电机工程学报, 2014, 34 (21): 3440-3447.

Zhang Xing, Guo Leilei, Yang Shuying, et al. Speed Sensorless Control of Permanent Magnet Synchronous Generators[J]. Proceedings of the CSEE, 2014, 34(21): 3440-3447.

[3]卫志农,俞小勇,吴佳佳.基于自抗扰控制的双馈发电机无速度传感器控制[J].电力自动化设备, 2011, 31 (1): 15-18.

Wei Zhinong, Yu Xiaoyong, Wu Jiajia. Speed Sensorless Control of DFIG Based on ADRC[J]. Electric Power Automation Equipment, 2011, 31(1): 15-18.

[4]王礼鹏,张化光,刘秀翀.低速PMSM无速度传感器调速系统积分滑模控制[J].电机与控制学报, 2012, 16(2): 19-31.

Wang Lipeng, Zhang Huaguang, Liu Xiuchong. Sensorless of Integral Sliding Mode Controlled PMSM at Low Speeds[J]. Electric Machines and Control, 2012, 16(2): 19-31.

[5]许波,朱熀秋,姬伟,等.改进型平方根无迹卡尔曼滤波及其在无轴承永磁同步电机无速度传感器运行中的应用[J].控制理论与应用, 2012, 29(1): 53-58.

Xu Bo, Zhu Huangqiu, Ji Wei, et al. Modified Square-root Unscented Kalman Filter and Its Application to Speed Sensorless Control of Bearingless Permanent Magnet Synchronous Motor[J]. Control Theory & Applications, 2012, 29(1): 53-58.

[6]王礼鹏, 张化光, 刘秀翀. 永磁同步电动机无速度传感器矢量调速系统的积分反步控制[J]. 控制理论与应用, 2012, 29(2): 199-204.

Wang Lipeng, Zhang Huaguang, Liu Xiuchong. Integral Backstepping Controller in the Sensorless Vector-control System for Permanent Magnet Synchronous Motor[J]. Control Theory & Applications, 2012, 29(2): 199-204.

[7]黄庆,黄守道,匡江传,等.基于模糊自抗扰的PMSM无速度传感器控制[J]. 湖南大学学报(自然科学版), 2012, 39(7): 37-43.

Huang Qing, Huang Shoudao, Kuang Jiangchuan, et al. PMSM Sensorless Control Based on Fuzzy Active-disturbance Rejection[J]. Journal of Hunan University(Natural Sciences), 2012, 39(7): 37-43.

[8]Hongryel K, Jubum S, Jangmyung L. A High-Speed Sliding-mode Observer for the Sensorless Speed Control of a PMSM[J]. IEEE Transactions on Industrial Electronics, 2011, 58(9): 4069-4077.

[9]Sun X D, Chen L, Yang Z B, et al. Speed-sensorless Vector Control of a Bearingless Induction Motor with Artificial Neural Network Inverse Speed Observer[J]. IEEE/ASME Transactions on Mechatronics, 2013, 18(4): 1357-1366.

[10]曾云,张立翔,于凤荣,等.电机实用参数描述的发电机哈密顿模型[J].中国电机工程学报, 2009, 29(27): 54-58.

Zeng Yun, Zhang Lixiang, Yu Fengrong, et al. Hamiltonian Model of Generator Described with Practical Parameters[J]. Proceedings of the CSEE, 2009, 29(27): 54-58.

[11]侯利民, 王巍. 无速度传感器的表面式永磁同步电机无源控制策略[J].控制与决策, 2013, 28(10): 1578-1586.

Hou Limin, Wang Wei. Speed Sensorless System of Passivity-based Control Strategy for SPMSM[J]. Control and Decision, 2013, 28(10): 1578-1586.

[12]任丽娜,刘福才,焦晓红,等.基于Hamilton模型的永磁同步风力发电系统中混沌运动的H∞控制[J]. 物理学报, 2012, 61(6): 77-82.

Ren Lina, Liu Fucai, Jiao Xiaohong, et al. Hamiltonian Model-basedH∞Control of Chaos Impermanent Magnet Synchronous Generators for Wind Power System[J]. Acta Phys. Sin., 2012, 61(6): 77-82.

[13]孙静,张承慧,裴文卉,等.考虑铁损的电动汽车用永磁同步电机Hamilton镇定控制[J].控制与决策, 2012, 27(12): 1899-1906.

Sun Jing, Zhang Chenghui, Pei Wenhui, et al. Hamiltonian Stabilizing Control of Permanent Magnet Synchronous Motor Considering Iron Loss for Electric Vehicle[J]. Control and Decision, 2012, 27(12): 1899-1906.

[14]梅生伟,申铁龙,刘志康.现代鲁棒控制理论与应用[M].北京: 清华大学出版社, 2008.

(编辑袁兴玲)

Speed SensorlessH∞Control for PMSM Based on Energy Function

Wu ZhongqiangWu ChanghanJia WenjingZhao Liru

Yanshan University,Qinhuangdao,Hebei,066004

Abstract:The speed sensorless H∞control method for PMSM was researched based on the energy function. In order to control the speed of motor rotator effectively, firstly the Hamilton model of the PMSM was shaped when there was not disturbances, and the rotator speed might reach the expected value. When there were disturbances, a H∞controller was designed based on the Hamilton function. An observer was designed using the method of expansion plus feedback based on the Hamilton function and used to measure the angular speed of rotator, and the speed sensorless shape plus H∞control were achieved. The simulation results show that the shape plus H∞control based on the observer can estimate the angular speed accurately, and restrain the disturbances of system, and control the rotator speed effectively.

Key words:energy function; permanent magnet synchronous motor(PMSM); speed sensorless; H∞control

作者简介：吴忠强，男，1966年生。燕山大学电气工程学院教授。研究方向为风力发电及控制。吴昌韩，男，1987年生。燕山大学电气工程学院硕士研究生。贾文静，女，1988年生。燕山大学电气工程学院硕士研究生。赵立儒，男，1988年生。燕山大学电气工程学院硕士研究生。

中图分类号：TM341；TH73

DOI：10.3969/j.issn.1004-132X.2016.05.003

基金项目：国家自然科学基金委员会与宝钢集团有限公司联合资助项目(U1260203)；河北省自然科学基金资助项目(F2012203088)

收稿日期：2015-05-11