模型约束基追踪反演方法

印兴耀,刘晓晶,吴国忱,宗兆云

(中国石油大学(华东)地球科学与技术学院,山东青岛266580)



模型约束基追踪反演方法

印兴耀,刘晓晶,吴国忱,宗兆云

(中国石油大学(华东)地球科学与技术学院,山东青岛266580)

摘要:基于反射系数奇偶分解的基追踪反演方法,补充了地震资料中所缺失的低频与高频信息,较好地提高了反演结果对地层的分辨能力。但仅仅使用稀疏约束加入的低频信息缺乏合理性,可能与工区的实际地质情况不符,需要进一步改善反演结果的横向连续性。因此,提出在基追踪反演目标函数中加入模型约束,得到模型约束的基追踪反演目标函数,并使用梯度投影稀疏重构(Gradient Projection for Sparse Reconstruction,GPSR) 算法进行求解。模型约束的加入增强了反演的稳定性,使得反演结果中的低频信息更加符合工区实际地质背景信息,并且能够改善反演结果的横向连续性。楔形模型和实际数据测试结果表明,模型约束基追踪反演方法不仅保持了基追踪反演的稀疏性,地层阻抗呈现块化,反射界面刻画清晰,而且反演方法更为稳定,反演结果的横向连续性得到了改善,从而验证了该方法的可行性。

关键词：模型约束;基追踪;地震反演;稀疏性;横向连续性

在线性系统假设前提下,ROBINSON[1]提出利用褶积模型描述地震响应,即地震记录可近似看作是地震子波与地层反射系数的褶积结果。自从TAYLOR等[2]提出确定性反褶积方法以来,基于褶积模型的反演方法成为了获取储层参数的重要方法。由于地震反演通常是一个病态问题,反演不稳定,因此需要加入一定的先验约束将不适定问题转化为近似适定问题。常规的反演方法通常是从地层的反射系数出发,假设反射系数是稀疏的,在稀疏约束条件下进行求解。反射系数的稀疏约束条件通常有Lp(p=0,1,2)范数[3],其中,基于L1范数的稀疏脉冲反演方法在储层预测中得到了广泛应用;或者假设反射系数服从一定的先验概率分布(如:HUBER分布[4]、柯西分布[5-6]、改进柯西分布[7-8]),通过贝叶斯理论在后验概率最大条件下建立目标函数进行反演,DUIJNDAM[9]和TARANTOLA[10]均对基于贝叶斯理论的反演方法进行了详细阐述。上述方法在增强反演方法稳定性与提高反演结果分辨率方面有一定的作用。随着油气勘探程度的不断深入,对反演结果的准确性、合理性以及分辨率提出了更高的要求。常规反演结果纵向上是平滑的,存在子波旁瓣效应,制约了我们利用反演结果对地层边界的识别。随着信号稀疏表示技术的快速发展,基于稀疏表示理论的反演方法也逐渐被应用到地震反演中,在确保可信度的基础上,利用稀疏表示理论反演,将地层的反演结果块化显示,反演结果对地层的分辨能力将会得到增强。THEUNE等[11]分析认为块化反演结果的分辨率更高,对地层的解释能力更强。ZHANG等[12-13]采纳了THEUNE等的观点，基于反射系数奇偶分解提出了基追踪反演方法,并应用于叠后与叠前地震资料,得到了块化的、更有利于地质解释的反演结果。针对基追踪反演横向连续性差的问题,ZHANG等[14]提出了基于空间正则化的多道基追踪反演方法,改善了反演结果的横向连续性。

由于基追踪反演中使用了L1范数的稀疏约束,稀疏约束能够补充地震资料缺少的低频与高频成分。但是,这样的低频成分缺乏实际工区的背景信息,并且基追踪反演方法的稳定性需要进一步加强。基于模型约束的地震反演方法能够较好地解决这两个问题。YIN等[15]和ZONG等[16-18]分别利用模型点约束与平滑模型约束增强反演的稳定性,并使得反演结果中的低频信息与实际工区地质背景相一致,从而使反演结果更为合理。为了增强基追踪反演方法的稳定性,改善其横向连续性,本文采用在Zhang等提出的基追踪反演的基础上,采纳Zong等提出的平滑模型约束的思想,在基追踪反演目标函数中加入模型约束性,在模型约束与稀疏约束的联合约束下,利用梯度投影稀疏重构(Gradient Projection for Sparse Reconstruction,GPSR)算法[19]进行求解。在确保反演结果稀疏性的基础上,增强反演的稳定性,改善反演结果的横向连续性,使得反演结果更为合理。

1反射系数奇偶分解

(1)

式中:re(i,j,Δt)为偶分量;ro(i,j,Δt)为奇分量;Δt为采样间隔;i为地层顶界面所对应的采样点位置；j为地层底界面所对应的采样点位置;a,b分别表示奇偶分解后偶分量与奇分量的系数。其中,奇偶反射系数对可以分别写作:

(2)

(3)

图1　稀疏脉冲反演与稀疏层反演研究对象a 稀疏脉冲反演研究对象; b 稀疏层反演研究对象

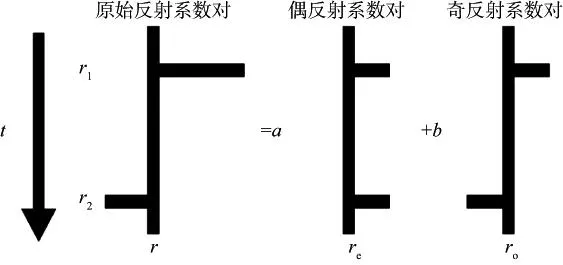
图2　反射系数对分量分解(根据Zhang等[13]修改)

ZHANG等[13]在应用反射系数奇偶分解的基础上考虑地层可能的厚度,构成奇偶反射对的楔形字典,并将单道反射系数序列用奇偶分量楔形字典表示:

(4)

式中:r为反射系数序列;ai,j为偶分量楔形字典的系数序列;bi,j为奇分量楔形字典的系数序列;I为单道采样点个数;J为地层最大可能厚度对应的采样点个数;D=[rero]为奇偶分量构成的楔形字典;m=[aTbT]T为楔形字典中对应的系数。

2模型约束基追踪反演

假设地层为水平层状介质,每一层为均匀各向同性完全弹性介质,根据Robinson褶积模型,地震资料中每一道地震数据由地震子波与地层反射系数序列褶积得到,考虑有噪声的情形,写成矩阵形式:

d=Wr+n

(5)

式中:d表示地震记录;W为子波矩阵;r为反射系数序列;n为噪声序列。

将(4)式代入(5)式可以得到:

d=WDm+n=Gm+n

(6)

式中:G为子波矩阵与楔形字典的乘积,G=WD。显然,矩阵G的列数远大于其行数,为欠定矩阵。根据稀疏表示理论,m为反射系数在矩阵G中的稀疏表示系数,即待反演参数。

ZHANG等[13]基于上述反射系数的奇偶分解,考虑地层的稀疏性,使用L1范数(即‖m‖1)对反演目标函数进行稀疏性约束,得到基于基追踪反演的目标函数:

(7)

在L1范数稀疏约束下,能够补充地震频带所缺失的低频与高频信息(图3),提高地震反演的分辨率。然而,PÉREZ等[20]认为这些信息是在数学假设的条件下获取的,缺乏实际工区的地质背景信息,并且ZHANG等[14]指出(7)式的反演结果缺乏横向连续性。利用测井资料建立低频模型对(7)式进行约束,可以有效补充低频信息,由于低频信息来自于实际工区的测井资料,因此,最终反演结果包含了工区内更多的真实背景,反演结果更为合理,并且模型约束能够有效地改善反演结果横向的连续性。

图3　地震反演补充低频与高频信息

在t时刻所对应的采样点上,纵波阻抗与反射系数之间的关系为:

(8)

将(8)式写作离散化的矩阵-向量形式:

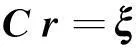
(9)

式中:C为积分矩阵;ξ为相对波阻抗序列。其表达式分别为:

(10)

(11)

因为反射系数在楔形字典分解如(4)式所示,所以(9)式可被写为:

CDm=ξ

(12)

利用拉格朗日乘子法,将模型约束加入到(7)式表示的基追踪反演的目标函数中,得到模型约束下反演的目标函数为:

(13)

基追踪极小化问题是一个凸优化问题,基追踪算法从字典中挑选的向量都是线性无关的,可以被理解为一种最佳基算法[21],(7)式是其标准形式。(13)式是稀疏约束与模型约束的联合约束下的目标函数,通过替换计算可以将其写作基追踪的标准形式。令:

(14)

则:

(15)

通过计算我们可以发现(13)式与(15)式等价,并且(15)式为基追踪的标准形式,因此我们将(15)式作为最终的模型约束下基追踪反演的目标函数。

3GPSR方法求解

随着稀疏表示技术的兴起,CHEN等[22]提出基追踪算法至今,其求解基追踪问题算法已成为研究的热点,大量文献中给出不同的求解算法[19,23-24]。本文选择GPSR算法对(15)式进行求解。

首先将待反演参数分解为正数序列和负数序列,对负数序列取相反数,则待反演参数m写作:m=u-v(u≥0,v>0),因此,待反演参数m的L1范数可以写作(16)式的形式：

(16)

进而将(16)式代入(15)式,则求解(15)式转为求解目标函数:

(17)

(18)

可以得到新的目标函数:

(19)

最终通过以下步骤进行迭代,可以求得(19)式的解。

1) 初始化,k=0,给定初始值z(0),选择参数β∈(0,1)与μ∈(0,0.5)。

2) 利用(20)式与(21)式计算α0,为了防止α0值过大,选取合适的αmin与αmax,并且有0<αmin<αmax,令α0=min{αmin,α0,αmax}。

(20)

(21)

(22)

4) 测试是否收敛,如果满足精度需求,则迭代终止;如果不满足精度需求,赋值k=k+1,返回步骤2)。

将反演得到的稀疏表示参数进一步利用(4)式转化为反射系数信息,最终利用(23)式将地层反射信息转化为地层的阻抗信息。

(23)

4模型测试

4.1楔形模型测试

模型约束基追踪反演结果呈现块化,对地层具有较好的分辨能力。首先测试模型约束基追踪反演对分辨能力的影响,将模型约束下基追踪反演方法应用于楔形模型。如图4所示,楔形模型的时间厚度为1～60ms。图4a为纵波阻抗模型剖面,上层纵波速度为2.2km/s,密度为2.36g/cm3;中间楔形体部分纵波速度为2.4km/s,密度为2.4g/cm3;楔形体下伏地层的纵波速度、密度值与楔形体上覆地层相同。反射系数是由反射界面两侧的阻抗差异引起的,图4b为利用图4a中相关参数计算得到的楔形体界面反射系数。利用35Hz雷克子波正演得到的无噪声合成记录如图4c所示。无噪声情况下反演的反射系数与阻抗分别如图4d与图4e所示,可以看出,反演得到的反射系数稀疏性好、连续性强,并且纵波阻抗呈块化显示,能够较好地识别楔形体的顶、底界面。图4中红色椭圆内,小于调谐厚度时反演得到的反射系数与阻抗值与真实模型存在细微的差别,但不影响我们对地层界面的识别。进一步验证该方法对数据中噪声的敏感性,在合成记录中加入服从高斯分布的随机噪声(图4f),信噪比为1。在含噪声情况下反演得到的反射系数和纵波阻抗分别如图4g和图4h所示。从图4g和图4h 可以看出,尽管在薄层处存在一定误差,但反演结果与真实模型仍具有较高的吻合度,反射系数所对应的界面连续性较好,纵波阻抗对地层的反射界面仍有很好的识别效果,无论是反射系数还是纵波阻抗所识别的反射界面与真实模型都相一致。因此,在原有的基追踪反演方法基础上加入模型约束不会改变反演结果对地层界面的识别能力,且能较好地改善反演结果的连续性。

图4　楔形模型叠后合成记录与反演结果a 楔形模型阻抗; b 真实反射系数; c 合成记录(无噪声); d 无噪声时的反射系数反演结果; e 无噪声时的阻抗反演结果; f 合成记录(信噪比为1); g 信噪比为1时反射系数反演结果; h 信噪比为1时阻抗反演结果

4.2二维模型资料测试

为了进一步验证本方法对实际资料的有效性和实用性,对更接近于实际情况的二维地震资料进行了相应的算法测试。在此,选用某二维地震记录作为测试数据,其叠加剖面如图5a所示,图中黑色的竖线为井所在位置。图5b为反演中所应用的平滑低频阻抗模型。图5c与图5d分别为反演得到的反射系数与纵波阻抗剖面。从图5中可以看出,反射系数具有较强的稀疏性,纵波阻抗的结果纵向上表现为块化,对地层分界面识别能力较强。

模型约束基追踪反演方法保持了反射系数反演的稀疏性,反演地层纵波阻抗以块化显示,地层界面识别明显,并且由于平滑模型的加入增强了反演的稳定性,改善了基追踪反演结果的横向连续性。如图5中箭头处所示,图5a中地震同相轴有较为明显的间断现象,图5c和图5d中反射系数和纵波阻抗反演结果均较为连续。

图6为由图5中提取的井旁道与常规反演结果的对比,从左至右依次为原始地震记录井旁道、井旁道反演结果合成记录、测井曲线计算的纵波阻抗曲线、模型约束下基追踪反演的纵波阻抗以及常规反演方法得到的纵波阻抗。

图5　Hampson-Russell软件中数据反演测试a 地震记录; b 阻抗模型; c 反演的反射系数; d 反演的阻抗

从图6可以看出,利用模型约束基追踪反演结果的合成记录与实际地震记录有较高的相似系数,验证了该方法反演结果的正确性。图6中,0.324～0.336s两条红线之间为一气层,比较模型约束基追踪反演方法与传统方法的反演结果可以看出,传统方法的反演结果是平滑的,对储层的边界刻画不够清晰,而本文方法的反演结果中,气层边界清晰,有很强的储层边界识别性能(图中绿色箭头处)。

图6　井旁道反演结果对比

5实际资料应用分析

将本文提出的模型约束基追踪反演方法应用到某实际工区的叠后地震资料中,叠后地震记录如图7a所示。图7b为反演过程中所使用的纵波阻抗平滑模型。图7c和图7d分别为采用本文提出的模型约束基追踪反演方法反演得到的反射系数与纵波阻抗。

从图7可以看出,反射系数稀疏,纵波阻抗呈现块化,对地层界面识别显著。图7a中黑色椭圆内为气藏发育区,但同相轴出现了较为明显的间断现象,经过模型约束基追踪反演方法反演得到的反射系数与纵波阻抗在椭圆框内地层连续,验证模型约束基追踪反演增强了反演的稳定性、改善了反演结果的连续性。

图7　实际工区地震记录与反演结果a 地震记录; b 纵波阻抗平滑模型; c 反射系数反演结果; d 纵波阻抗反演结果

6结论

本文在Zhang等提出的基追踪反演的基础上加入模型约束,得到模型约束条件下的基追踪反演目标函数,使得反演结果中的低频信息更加符合工区内的实际地质背景信息,从而使得反演结果更加合理,增强了反演的稳定性,在一定程度上改善了反演结果的横向连续性。

由于反演目标函数中存在L1范数稀疏约束,利用GPSR基追踪反演算法能够在反演结果合理的条件下,确保反射系数反演结果的稀疏性。在反射系数稀疏的条件下,阻抗反演结果表现为块化,能够有效地消除子波旁瓣的影响,对地层边界的识别更有优势。

参考文献

[1]ROBINSON E.Predictive decomposition of seismic traces[J].Geophysics,1957,22(4):767-778

[2]TAYLOR H,BANKS S,MC COY J.Deconvolution with theL1norm[J].Geophysics,1979,44(1):39-52

[3]DEBREYE H W J,RIEL P V.Lp-norm deconvolution[J].Geophysical Prospecting,1990,38(4):381-403

[4]GUITTON A,SYMES W W.Robust inversion of seismic data using the Huber norm[J].Geophysics,2003,68(4):1310-1319

[5]张世鑫,印兴耀,张繁昌.基于三变量柯西分布先验约束的叠前三参数反演方法[J].石油地球物理勘探,2011,46(5):737-743

ZHANG S X,YIN Y X,ZHANG F C.Prestack three term inversion method based on Trivariate Cauchy distribution prior constraint [J].Oil Geophysical Propecting,2011,46(5):737-743

[6]雷文文,印兴耀,张繁昌.三元柯西约束叠前地震横波速度反演[C]∥中国地球物理学会.中国地球物理(2011).合肥:中国科学技术大学出版社，2011：649

LEI W W,YIN X Y,ZHANG F C.Seismic prestack shear wave velocity inversion via a Trivariate Cauchy probability distribution[C]∥Chinese Geophysical Society.The Chinese geophysical (2011).Hefei:University of Science and Technology of China Press,2011:649

[7]宗兆云,印兴耀,张繁昌.基于改进柯西约束和点约束的稀疏脉冲弹性阻抗反演[C]∥中国地球物理学会.中国地球物理(2009).合肥:中国科学技术大学出版社,2009:204

ZONG Z Y,YIN X Y,ZHANG F C.Sparse spike elastic inversion based on new Cauchy and points constraint[C]∥Chinese Geophysical Society.The Chinese geophysical(2009).Hefei:University of Science and Technology of China Press,2009:204

[8]杨培杰,印兴耀.非线性二次规划贝叶斯叠前反演[J].地球物理学报,2008,51(6):1876-1882

YANG P J,YIN X Y.Non-linear quadratic programming Bayesian prestack inversion[J].Chinese Journal of Geophysics,2008,51(6):1876-1882

[9]DUIJNDAM A J W.Detailed Bayesian inversion of seismic data[D].The Netherlands:Technische Universiteit Delft,1987

[10]TARANTOLA A.Inverse problem theory and methods for model parameter estimation[M].Philadelphia:Society for Industrial and Applied Mathematics,2005:1-37

[11]THEUNE U,JENSÅS I Ø,EIDSVIK J.Analysis of prior models for a blocky inversion of seismic AVA data[J].Geophysics,2010,75(3):C25-C35

[12]ZHANG R,SEN M K,SRINIVASAN S.A prestack basis pursuit seismic inversion[J].Geophysics,2013,78(1):R1-R11

[13]ZHANG R,CASTAGNA J.Seismic sparse-layer reflectivity inversion using basis pursuit decomposition[J].Geophysics,2011,76(6):R147-R158

[14]ZHANG R,SEN M K,SRINIVASAN S.Multi-trace basis pursuit inversion with spatial regularization[J].Journal of Geophysics and Engineering,2013,10(3):35012

[15]YIN X Y,YANG P J,ZHANG G Z.A novel prestack AVO inversion and its application[J].Expanded Abstracts of 78thAnnual Internat SEG Mtg,2008,2041-2045

[16]ZONG Z Y,YIN X Y,WU G C.AVO inversion and poroelasticity with P- and S-wave moduli[J].Geophysics,2012,77(6):N17-N24

[17]ZONG Z,YIN X,WU G.Direct inversion for a fluid factor and its application in heterogeneous reservoirs[J].Geophysical Prospecting,2013,61(5):998-1005

[18]ZONG Z,YIN X,WU G.Elastic impedance variation with angle inversion for elastic parameters[J].Journal of Geophysics and Engineering,2012,9(3):247-260

[19]FIGUEIREDO M A T,NOWAK R D,WRIGHT S J.Gradient projection for sparse reconstruction:application to compressed sensing and other inverse problems[J].IEEE Journal of Selected Topics in Signal Processing,2007,1(4):586-597

[20]PÉREZ D,VELIS D,SACCHI M.High-resolution prestack seismic inversion using a hybrid FISTA least-squares strategy[J].Geophysics,2013,78(5):R185-R195

[21]MALLAT S.A wavelet tour of signal processing:the sparse way[M].3rded.Salt Lake City:Academid Press,2008:611-696

[22]CHEN S S,DONOHO D L,SAUNDERS M A.Atomic decomposition by basis pursuit[J].Siam Review,2001,43(1):129-159

[23]BERG E V D,FRIEDLANDER M P.Probing the Pareto frontier for basis pursuit solutions[J].Siam Journal on Scientific Computing,2008,31(2):890-912

[24]YANG J,ZHANG Y.Alternating direction algorithms forL1-problems in compressive sensing[J].Eprint Arxiv,2009,33(1):250-278

(编辑：顾石庆)

Basis pursuit inversion method under model constraint

YIN Xingyao,LIU Xiaojing,WU Guochen,ZONG Zhaoyun

(SchoolofGeosciences,ChinaUniversityofPetroleum,Qingdao266580,China)

Abstract:The basis pursuit inversion (BPI) method based on the dipole decomposition of reflection coefficients compensates the low-frequency and high-frequency information lacked in the seismic data,which can well improve the identification capability of inversion results on formations.However,it might not be reasonable to add the low frequency information just by the sparse constraint,and the information might not coincide with the true geological background.Therefore,we derived the model constrained BPI objective function by putting the model constraint to the origin objective function of BPI,and utilized the gradient projection for sparse reconstruction (GPSR) algorithm to solve the problem.It would not only enhance the inversion stability and make the low frequency information contained in inversion results more consistent with the actual work area,but also improve the lateral continuity of the inversion results.The results of the wedge model and real field data testing demonstrate that the model constrained BPI method not only keep the sparsity of the inversion results and shows the impedance in blocky,which characterizes the interface more clearly and improves the reliability of the inversion and the lateral continuity of the inversion results.

Keywords:model constraint,basis pursuit,seismic inversion,sparsity,lateral continuity

文章编号：1000-1441(2016)01-0115-08

DOI:10.3969/j.issn.1000-1441.2016.01.015

中图分类号：P631

文献标识码：A

基金项目：国家自然科学基金石油化工联合基金重点项目(U1562215)、国家重点基础研究发展计划(973计划)项目(2013CB228604)与国家科技重大专项(2011ZX05030-004-002,2011ZX05006-002,2011ZX05009-003)联合资助。

作者简介：印兴耀(1962—),男,教授,博士生导师,从事勘探地球物理理论与方法的教学与科研工作。

收稿日期：2014-02-25;改回日期：2015-06-28。

印兴耀,刘晓晶,吴国忱,等.模型约束基追踪反演方法[J].石油物探,2016,55(1):-122

YIN Xingyao,LIU Xiaojing,WU Guochen,et al.Basis pursuit inversion method under model constraint[J].Geophysical Prospecting for Petroleum,2016,55(1):-122

This research is financially supported by the Petrochemical Joint Foundation Major Project of National Natural Science Foundation of China (Grant No.U1562215),the National Key Basic Research Program of China (973 Program) (Grant No.2013CB228604) and the National Science and Technology Major Project of China (Grant Nos.2011ZX05030-004-002,2011ZX05006-002,2011ZX05009-003).