非均匀节点网格TI介质反射波射线追踪研究

黄光南,邓居智,李红星,李泽林,张　华,王安东

(1.东华理工大学核技术应用教育部工程研究中心,江西南昌 330013;2.中国地质大学(武汉)地球内部多尺度成像湖北省重点实验室,湖北武汉 430074;3.中国石油大学(北京)油气资源与探测国家重点实验室,北京 102249)



非均匀节点网格TI介质反射波射线追踪研究

黄光南1,2,3,邓居智1,李红星1,李泽林1,张华1,王安东1

(1.东华理工大学核技术应用教育部工程研究中心,江西南昌 330013;2.中国地质大学(武汉)地球内部多尺度成像湖北省重点实验室,湖北武汉 430074;3.中国石油大学(北京)油气资源与探测国家重点实验室,北京 102249)

摘要:地下介质不仅具有各向异性性质,还存在一定程度的复杂地质构造。运用均匀节点网格射线追踪方法计算旅行时要求网格单元的划分非常小以达到较高的旅行时精度,这种做法会产生大量的网格单元从而降低计算效率。基于均匀节点网格算法,研究了非均匀节点网格TI介质反射波射线追踪方法,采用较大的网格单元,通过在网格单元的每条边增加次一级节点来提高旅行时计算的精度与效率。首先讨论了qP,qSV和qSH波的群速度计算方法,然后给出了非均匀节点网格TI介质反射波射线追踪算法,最后分别求取了3种不同对称轴倾角的TI介质起伏地层模型qP,qSV和qSH反射波的射线路径和旅行时。结果表明:①非均匀节点网格射线追踪算法能够适用于复杂TI介质模型;②相同模型中不同波模式具有不同的反射路径和旅行时;③相同波模式在不同对称轴倾角模型中也具有不同的反射路径和旅行时。

关键词：起伏地层模型;非均匀节点网格;各向异性TI介质;射线追踪算法

各向异性介质射线追踪可以模拟地震波在复杂地下介质中的传播，为实际地震资料解释提供有效的技术手段，因而被广泛应用于各向异性地震记录合成、各向异性参数反演、各向异性地震偏移成像等技术领域。国外学者对各向异性介质射线追踪技术的研究较早[1-2]。如CERVENY[3]推导了不均匀各向异性介质射线走时和振幅的计算方法,为实施射线追踪算法奠定了理论基础;CERVENY等[4]针对非均匀、弱各向异性介质情形,提出了无需射线追踪的线性化走时计算方法;GAJEWSKI等[5]将打靶法射线追踪技术成功扩展至地层起伏变化的三维各向异性介质模型,通过数值模拟计算得到了射线路径、旅行时和射线振幅信息;SHEARER等[6]利用线性梯度算法刻画各向异性介质模型,通过求解多项式方程得到射线路径与旅行时,利用数值模拟结果展示了相关理论和算法的有效性。

国内最早计算各向异性旅行时的方法基于时距曲线方程。例如:张文生等[7]推导了水平层状各向异性介质走时近似公式,通过数值模拟P波和SV波时距曲线,验证了近似表达式的有效性;苑书金等[8]利用泰勒级数法推导了P波和SV波在短、中、长排列的反射波旅行时公式,通过数值模拟验证了这种计算方法的有效性和可行性。后来,国内学者逐渐提出了算法相对简单的各向异性射线追踪方法。例如:邓怀群等[9]根据群速度和相速度的关系,结合各向异性射线参数表达式,推导出了射线追踪的射线参数表达式;孔选林等[10]利用逐段迭代射线追踪方法计算简单层状各向异性模型的地震波走时,有效地模拟了P波和SV波的时距曲线;熊金良等[11]利用水平层状介质时距曲线方程和二分法射线追踪算法计算层状各向异性模型的方位旅行时,当地下存在裂隙时,不同方位的时距曲线之间存在较大差别;李建国等[12]将试射法射线追踪算法应用于VTI介质理论模型研究,利用VSP观测系统计算了上、下行P波的射线路径和旅行时;郝奇等[13]基于二维层状VTI介质模型推导了qP波和qSV波的精确Snell定律公式,归纳了VTI介质qP波和qSV波的射线追踪算法流程,通过水平和起伏界面模型的反射波射线追踪数值模拟,证明了该算法的准确性和高效性。

上述地球物理学者研究各向异性射线追踪时,大多采用地层对称轴倾角垂直的VTI介质,因为它是最为简单的一种各向异性介质情形,利用它推导的射线追踪算法可以避免相对复杂的计算。如QIAN等[14]通过建立群速度和相速度之间的显式关系式寻找有限差分走时场的外推方向,方便地求出各向异性介质qP波的初至走时信息,通过二维和三维VTI介质数值模拟实验,证明了该方法具有较高的数值精度和运算效率。刘玉柱等[15]实现了VTI介质射线追踪算法,采用两步法反演两个Thomsen参数,针对异常体模型的反演取得了较好的数值效果。SCHNEIDER[16]利用扰动理论来求解P波的程函方程,当各向异性强度在一定范围内时,计算得到的各向异性旅行时具有较高的精度。然而,自然界地层形成之后往往会伴随一系列的地壳运动,导致地层对称轴倾角发生变化;因此,野外实际地层大多数属于TTI介质情形。ZHOU等[17]将最短路径射线追踪算法拓展至各向异性TTI介质情形,计算了倾斜界面模型3种体波的射线路径和旅行时。WANG[18]针对各向异性介质弯曲射线法产生的高度非线性问题修改了牛顿迭代法,用于求解稳定非线性问题,并利用井间观测方式反演了各向异性介质模型参数。赵后越等[19]结合均匀节点网格和非均匀节点网格算法实现了起伏地表各向异性TTI介质的射线追踪,理论模型试算结果表明该方法具有较高的数值精度。QIN等[20]根据惠更斯原理推导了各向异性介质初至波走时的计算方法,并将该方法应用于几种各向异性TTI介质模型,通过与波动方程所得旅行时相比,说明它是一种稳定和精确的各向异性射线追踪算法。WANG等[21]针对复杂各向异性TTI介质,利用基于网格的射线追踪算法,反演得到了模型的各向异性参数剖面。KUMAR等[22]针对各向异性TTI介质,提出了一种直接计算P波初至走时的方法,并将它与克希霍夫积分偏移算法相结合,极大地改善了偏移成像的精度。PRATT等[23]运用弯曲射线追踪算法反演井间各向异性TTI介质的参数分布和地层的对称轴倾角。LOU[24]将求解程函方程的快速匹配方法用于TTI介质的初至旅行时求取,数值实例表明它是一种稳定和精确的初至旅行时计算方法。本文研究非均匀节点网格各向异性TI介质反射波射线追踪算法,它不仅适用于任意对称轴倾角的地层模型,也适用于起伏地层模型,其运用条件更加贴近于实际地质情形。

1各向异性介质群速度计算方法

各向同性介质射线追踪算法基于速度网格模型,而各向异性TI介质射线追踪算法基于群速度网格模型。ZHOU等[25]提出了两种计算各向异性介质群速度的方法:特征值法和特征向量法。对于二维各向异性模型,根据弹性模量参数{c11,c13,c33,c44,c66},利用特征值法可以得到群速度在水平与垂直方向的表达式为:

(1)

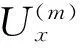
(2)

其中,∂vm/∂ϑ是相速度表达式对ϑ的偏导数,计算公式如下:

(3)

其中,

(4)

式中:v1,v2和v3分别代表qP波、qSV波和qSH波速度;c11,c13,c33,c44,c66为弹性模量参数。DALEY等[27]给出了各向异性介质的相速度表达式,即克里斯托弗矩阵的特征值:

(5)

P和Q的表达式为:

Q=Q1Q2-Q3

(6)

其中Q1,Q2和Q3的表达式为:

Q1=c44cos2ϑ+c11sin2ϑ

Q2=c33cos2ϑ+c44sin2ϑ

(7)

公式(2)至公式(7)中,角度ϑ为相慢度向量n=(sinθ,cosθ)和各向异性介质对称轴倾角方向ez=(sinθ0,cosθ0)之间的夹角。

2非均匀节点网格TI介质反射波射线追踪算法

与各向同性介质旅行时计算方法类似,各向异性介质也可以利用线性积分沿着射线路径计算旅行时,计算表达式为:

(8)

式中:x为空间坐标向量,r0是射线方向从xA到xB的单位向量,ds为沿射线路径的线段。由(8)式可知旅行时计算需要确定群速度U(x,θ0,r0)和射线路径R(x)。第1节给出了群速度计算方法,这里讨论如何计算旅行时。根据费马原理,在空间位置xB处的旅行时计算表达式为:

(9)

其中,ΩB是模型内xB点的邻域。将(9)式与最短路径射线追踪算法结合,可以得到各向异性射线追踪算法。下面介绍各向异性TI介质非均匀节点网格反射波射线追踪算法的实现步骤。

1) 划分非均匀节点网格参数模型。固定网格单元大小,将二维各向异性模型m(x)划分成由主节点组成的网格模型:

(10)

其中,Nx,Nz分别代表x和z轴方向的网格个数。这样模型就可以用很多矩形网格组成,每个矩形网格的4个角被定义为主节点。根据这种网格划分方法,通常需要将模型划分为非常小的网格以获得较高的旅行时计算精度。采用BAI等[28]提出的非均匀节点网格算法将模型划分为较大的网格单元,通过在网格单元的每条边增加次一级节点来提高旅行时计算的精度与效率;将网格模型转化成群速度模型Um(xk,θ0,r0),m=1,2,3分别对应qP波、qSV波和qSH波。如果次一级的网格节点数为N2,那么网格模型的节点总数为N1+N2。另外,如果炮点、检波点位置和网格模型的节点位置不重合,那么必须增加炮点和检波点位置节点。因此整个模型包括3类网格节点:主节点、次节点、炮点和检波点位置对应的节点。

2) 初始化走时场。对炮点所在节点的走时赋初值0,其它网格节点的走时赋初值无穷大(例如107),从炮点所在节点开始,计算炮点周围节点的走时,再从相邻节点计算其它节点的走时,并记录相邻节点的走时最小值。

3) 非均匀节点网格初至波走时计算。单个网格内部两个节点之间的旅行时可以利用如下公式计算:

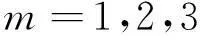
(11)

4) 非均匀节点网格反射波旅行时计算。如果各向异性模型存在复杂的地层界面,那么地震波会在界面处产生反射波。可以用一系列密集的网格节点来代表地层界面,地层界面节点与前述3类节点组合起来,可以得到一个新的节点集合,它包括主节点、次节点、反射界面节点和炮、检点位置节点。每个地层界面对应的反射波旅行时τ的计算表达式为:

(12)

其中,τS(xint)和τR(xint)分别是炮点S与检波点R到界面节点位置xint的初至走时,Ωint代表反射界面节点的集合。在反射波旅行时计算过程中,分别假设炮点S与检波点R为震源点位置,进行两次正演走时计算,然后以(12)式为准则寻找相应的界面反射节点,从而求取反射波的旅行时与射线路径。值得注意的问题是:在计算反射波旅行时时,群速度模型只与反射界面以上的非均匀节点网格模型有关,也就是说,在计算τS(xint)和τR(xint)时,只需要截取反射界面以上非均匀节点网格模型参与运算,因此可以提高算法的整体运算效率。

5) 非均匀节点网格反射波射线路径求取。当炮点和检波点分别完成走时计算后,从非均匀节点网格模型中得到入射节点系列,根据入射节点(它包括主节点、次节点和界面节点)的序号以反向追踪的形式求取连接检波点与炮点之间的射线路径,从而得到共炮点道集的射线路径。根据这种方法可以获得所有炮点对应的检波点的射线路径。

3数值模拟

利用非均匀节点网格射线追踪算法对长度800m,深度500m的起伏地层各向异性模型进行了射线追踪数值模拟。该模型含有两个起伏界面和一个水平界面,第一层介质的弹性模量参数为c11=9.08,c13=2.98,c33=7.53,c44=2.27,c66=3.84,第二层介质的弹性模量参数为c11=20.3,c13=9.58,c33=22.3,c44=8.35,c66=11.35,第三层介质的弹性模量参数为c11=13.86,c13=4.31,c33=10.93,c44=3.31,c66=4.34。炮点位于地表400m处,检波点共33个,第1个检波点位于地表0处,第33个检波点位于800m处,检波点间距为25m(参见图1)。

图1给出了网格模型的主节点和次节点分布。为了方便图形显示和易于理解,这里假设模型的网格间距为50m,那么主节点数为187个;网格的每条边增加1个次一级节点,那么次一级节点数为346个,主次节点的总数为533个。由于网格间距较大,计算效率相对较高;同时,网格模型的主次节点数较大,算法的旅行时计算精度也相对较高。图2 为qP波在模型内部的波前等值线图,与均匀节点网格算法产生的波前等值线图相比,由于它采用了大量的次一级网格节点,其波前等值线不够光滑,但是它具有较高的数值精度。为了提高旅行时的数值精度,模型的网格间距在水平与垂直方向上均为5m,在网格单元的每一条边增加7个次一级网格节点,这样一个网格单元的主次节点数为32个。这里研究第一层和第二层介质对称轴倾角分别为0,45°和90°(VTI,TTI和HTI)时,qP,qSV与qSH反射波的射线路径和旅行时分布。图3至图5 是地层对称轴倾角为0时,qP,qSV与qSH反射波的射线路径和旅行时分布。图6至图8是地层对称轴倾角为45°时,qP,qSV与qSH反射波的射线路径和旅行时分布。图9至图11是地层对称轴倾角为90°时,qP,qSV与qSH反射波的射线路径和旅行时分布。比较这3组各向异性模型射线追踪结果可以看出,对于同一各向异性模型,不同波模式(qP,qSV与qSH波)具有不同的反射波射

图1　模型内部的非均匀节点网格剖分(白色实心圆代表主节点;白色空心圈代表次节点;红色菱形点代表界面节点)

线路径和旅行时分布(图3,图4和图5);当地层对称轴倾角不同时,同一波模式的反射波射线路径和旅行时分布也不相同(图3,图6和图9)。

图2　模型内部的波前等值线(qP波)

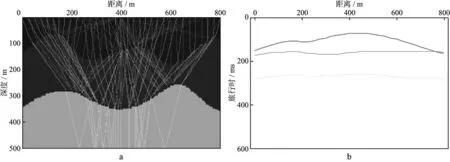
图3　地层对称轴倾角为0时qP波的射线路径(a)和旅行时分布(b)

图4　地层对称轴倾角为0时qSV波的射线路径(a)和旅行时分布(b)

图5　地层对称轴倾角为0时qSH波的射线路径(a)和旅行时分布(b)

图6　地层对称轴倾角为45°时qP波的射线路径(a)和旅行时分布(b)

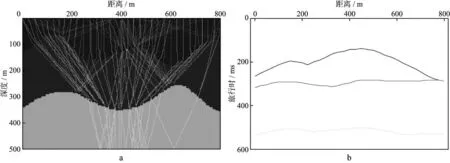
图7　地层对称轴倾角为45°时qSV波的射线路径(a)和旅行时分布(b)

图8　地层对称轴倾角为45°时qSH波的射线路径(a)和旅行时分布(b)

图9　地层对称轴倾角为90°时qP波的射线路径(a)和旅行时分布(b)

图10　地层对称轴倾角为90°时qSV波的射线路径(a)和旅行时分布(b)

图11　地层对称轴倾角为90°时qSH波的射线路径(a)和旅行时分布(b)

4结束语

本文研究的非均匀节点网格TI介质射线追踪技术可以在较少的网格单元数情况下,同时兼顾数值精度和运算效率。首先求取各向异性群速度模型,然后结合群速度模型和最短路径射线追踪算法求取射线路径和旅行时,最后根据入射节点在非均匀节点网格模型内的序号反向追踪,求取连接炮点和检波点之间的射线路径。由于qP,qSV和qSH波的群速度表达式不同,因此需要分别求取这3种波模式的射线路径和旅行时。对于同一各向异性模型,不同波模式具有不同的反射波射线路径和旅行时。对于不同对称轴倾角模型,同一种波模式的反射波射线路径和旅行时也不相同。作为一种正演技术,这种非均匀节点网格TI介质反射波射线追踪算法在复杂地层各向异性参数反演和各向异性地震偏移等领域具有广泛的应用前景。

致谢:感谢阿拉伯联合酋长国石油大学周兵教授对本文给予的指导和帮助。

参考文献

[1]BABICH V M.Ray method for the computation of the intensity of wave fronts in elastic inhomogeneous anisotropic medium:problems of the dynamic theory of propagation of seismic waves[M].Saint Petersburg:Leningrad University Press,1961:36-46

[2]CERVENY V.Seismic ray theory[M].Cambridge:Cambridge University Press,2001:234-400

[3]CERVENY V.Seismic rays and ray intensities in inhomogenous anisotropic media[J].Geophysical Journal of the Royal Astronomical Society,1972,29:1-13

[4]CERVENY V,FIRBAS P.Numerical modeling and inversion of traveltimes of seismic body waves in inhomogeneous anisotropic media[J].Geophysical Journal of the Royal Astronomical Society,1984,76:41-51

[5]GAJEWSKI D,PSENCIK I.Computation of high-frequency seismic wavefields in 3-D laterally inhomogeneous anisotropic media[J].Geophysical Journal of the Royal Astronomical Society,1987,91:383-411

[6]SHEARER P M,CHAPMAN C H.Ray tracing in anisotropic media with a linear gradient[J].Geophysical Journal International,1988,94(3):575-580

[7]张文生,何樵登.横向各向同性介质中的反射波时距曲线[J].石油物探,1997,36(2):15-24

ZHANG W S,HE Q D.Reflection time-distance curves in transversely isotropic media[J].Geophysical Prospecting for Petroleum,1997,36(2):15-24

[8]苑书金,董敏煜,魏修成,等.横向各向同性介质中的反射波旅行时分析[J].石油地球物理勘探,2001,36(4):488-494

YUAN S J,DONG M Y,WEI X C,et al.Analysis of reflection travel-time in transversely isotropic media[J].Oil Geophysical Prospecting,2001,36(4):488-494

[9]邓怀群,刘雯林,赵正茂.横向各向同性介质中纵波和转换横波的快速射线追踪方法[J].石油物探,2000,39(4):1-11

DENG H Q,LIU W L,ZHAO Z M.Fast ray tracing method for compressional and conveted waves in transversely isotropic media[J].Geophysical Prospecting for Petroleum,2000,39(4):1-11

[10]孔选林,李录明,罗省贤,等.各向异性介质中地震波射线正演[J].物探化探计算技术,2008,30(3):178-184

KONG X L,LI L M,LUO S X,et al.Seismic wave ray forward in anisotropy medium[J].Computing Techniques for Geophysical and Geochemical Exploration,2008,30(3):178-184

[11]熊金良,刘洋,侯伯刚.任意各向异性介质方位旅行时正演[J].石油地球物理勘探,2005,40(3):300-304

XIONG J L,LIU Y,HOU B G.Azimuth travel time forward modeling in arbitrary anisotropic media[J].Oil Geophysics Prospecting,2005,40(3):300-304

[12]李建国,李彦鹏,郭晓玲.VTI介质试射射线追踪[J].石油地球物理勘探,2010,45(4):491-496

LI J G,LI Y P,GUO X L.VTI medium test firing ray tracing[J].Oil Geophysics Prospecting,2010,45(4):491-496

[13]郝奇,何樵登,王德利,等.二维层状VTI介质的梯形块状建模及qP/qSV反射波运动学射线追踪[J].石油地球物理勘探,2009,44(6):662-670

HAO Q,HE Q D,WANG D L,et al.Trapezoid block modeling and qP/qSV reflection wave kinematic ray tracing in 2D layered VTI media[J].Oil Geophysical Prospecting,2009,44(6):662-670

[14]QIAN J,SYMES W W.Finite-difference quasi-P traveltimes for anisotropic media[J].Geophysics,2002,67(1):147-155

[15]刘玉柱,王光银,董良国,等.VTI介质多参数联合走时层析成像方法[J].地球物理学报,2014,57(10):3402-3410

LIU Y Z,WANG G Y,DONG L G,et al.Joint inversion of VTI parameters using nonlinear traveltime tomography[J].Chinese Journal of Geophysics,

2014,57(10):3402-3410

[16]SCHNEIDER W A.Linearization of the P-wave eikonal equation for weak vertical transverse isotropy[J].Geophysics,2003,68(3):1075-1082

[17]ZHOU B,GREENHALGH S A.Ray path and travel time computations for 2D transversely isotropic media with dipping symmetry axes[J].Exploration Geophysics,2006,37(2):150-159

[18]WANG Y H.Seismic ray tracing in anisotropic media:a modified Newton algorithm for solving highly nonlinear systems[J].Geophysics,2014,79(1):T1-T7

[19]赵后越,张美根.起伏地表条件下各向异性地震波最短路径射线追踪[J].地球物理学报,2014,57(9):2910-2917

ZHAO H Y,ZHANG M G.Tracing seismic shortest path rays in anisotropic medium with rolling surfacing[J].Chinese Journal of Geophysics,2014,57(9):2910-2917

[20]QIN F,SCHUSTER G.First-arrival travel time calculation for anisotropic media[J].Geophysics,1993,58(9):1349-1358

[21]WANG X X,TSVANKIN I.Ray-based gridded tomography for tilted transversely isotropic media[J].Geophysics,2013,78(1):C11-C23

[22]KUMAR D,SEN M K,FERGUSON R J.Travel time calculation and prestack depth migration in tilted transversely isotropic media[J].Geophysics,2004,69(1):37-44

[23]PRATT R G,CHAPMAN C H.Travel time tomography in anisotropic media (Ⅱ):application[J].Geophysical Journal International,1992,109(1):20-37

[24]LOU M.Travel time calculation in 3D TTI media by the fast marching method[J].68thEAGE Conference and Exhibition,2006:H034

[25]ZHOU B,GREENHALGH S A.On the computation of elastic wave group velocity for a general anisotropic medium[J].Journal of Geophysics and Engineering,2004,1(3):205-215

[26]CRAMPIN S.A review of wave motion in anisotropic and cracked elastic-media[J].Wave Motion,1981,3(4):343-391

[27]DALEY P,HRON F.Reflection and transmission coefficients for transversely isotropic media[J].Bulletin of the Seismological Society of America,1977,67(3):661-675

[28]BAI C Y,GREENHALGH S A,ZHOU B.3D ray tracing using a modified shortest-path method[J].Geophysics,2007,72(4):T27-T36

(编辑：戴春秋)

Reflected wave ray tracing in TI medium based on the nonuniform node meshes

HUANG Guangnan1,2,3,DENG Juzhi1,LI Hongxing1,LI Zelin1,ZHANG Hua1,WANG Andong1

(1.EngineeringResearchCenterofNuclearTechnologyApplication,MinistryofEducation,Nanchang330013,China;2.HubeiSubsurfaceMulti-scaleImagingKeyLaboratory(SMIL),ChinaUniversityofGeosciences,Wuhan430074,China;3.StateKeyLaboratoryofPetroleumResourcesandProspecting,ChinaUniversityofPetroleum,Beijing102249,China)

Abstract:The actual stratum not only has anisotropic property,but also has complicated geological structure to some extent.The efficiency of uniform grid ray tracing method is poor because there are too many cells caused by the refining grid algorithm.The ray tracing algorithm based on the nonuniform node meshes can obtain much higher numerical resolution and computational efficiency even with less primary node number and some secondary node number.Firstly,the calculation of the group velocities for qP,qSV and qSH waves are discussed in this article.Then,the reflected wave ray tracing in TI media is realized by combining these group velocities with the ray tracing algorithm based on the nonuniform node meshes.Finally,three undulating-layered TI models with different symmetry axes are built,the raypaths and traveltime of the qP,qSV and qSH reflected waves are computed for these models respectively.The numerical simulation results suggest that:①the ray tracing algorithm based on the nonuniform node meshes has applicability for such a complex TI media;②three wave-modes have different raypaths and traveltimes for the same model;③the same wave-mode also has different raypaths and traveltime for the model with different symmetry axes.

Keywords:undulating-layered model,nonuniform node meshes,anisotropic TI media,ray tracing algorithm

文章编号：1000-1441(2016)01-0025-08

DOI:10.3969/j.issn.1000-1441.2016.01.004

中图分类号：P631

文献标识码：A

基金项目：国家科技重大专项(2011ZX05024-001-02)、国家自然科学基金(41504095,41004048,41364004,41104074,41304097)、国家科技支撑计划(2011BAB04B03)、东华理工大学博士科研启动基金(DHBK2013212)、核技术应用教育部工程研究中心基金(HJSJYB2015-9)、中国地质大学(武汉)地球内部多尺度成像湖北省重点实验室基金(SMIL-2015-10)和江西省教育厅基金(GJJ14476)项目联合资助。

作者简介：黄光南(1983—),男,博士,讲师,主要从事地震速度层析成像和地震数字处理方法研究。

收稿日期：2015-05-04;改回日期：2015-09-27。

黄光南,邓居智,李红星,等.非均匀节点网格TI介质反射波射线追踪研究[J].石油物探,2016,55(1):-32

HUANG Guangnan,DENG Juzhi,LI Hongxing,et al.Reflected wave ray tracing in TI medium based on the nonuniform node meshes[J].Geophysical Prospecting for Petroleum,2016,55(1):-32

This research is financially supported by the National Science and Technology Major Project of China (Grant No.2011ZX05024-001-02),National Natural Science Foundation of China (Grant Nos.41504095,41004048,41364004,41104074,41304097),National Science and Technology Supported Program (Grant No.2011BAB04B03),Doctoral Research Foundation of East China University of Technology (Grant No.DHBK2013212),Foundation of the Engineering Research Center of Nuclear Technology Application,Ministry of Education (Grant No.HJSJYB2015-9),Foundation of Hubei Subsurface Multi-scale Imaging Key Laboratory,China University of Geosciences (Grant No.SMIL-2015-10),Foundation of Education Department of Jiangxi Province (Grant No.GJJ14476).