贴体坐标系二维声波方程SBP有限差分法的稳定性分析

王　颖,周　辉,盛善波

(1.中国石油大学(北京)油气资源与探测国家重点实验室,中国石油大学(北京)CNPC物探重点实验室,中国石油大学(北京),北京102249；2.中国石油天然气勘探开发公司,北京100034)



贴体坐标系二维声波方程SBP有限差分法的稳定性分析

王颖1,周辉1,盛善波2

(1.中国石油大学(北京)油气资源与探测国家重点实验室,中国石油大学(北京)CNPC物探重点实验室,中国石油大学(北京),北京102249；2.中国石油天然气勘探开发公司,北京100034)

摘要:有限差分方法(Finite Difference Method,FDM)是波动方程正演数值模拟领域应用最为广泛的方法之一,然而,当模拟区域不规则或者地表起伏不平时,规则网格有限差分法求解波动方程会产生阶梯状近似,影响模拟的精度。借助贴体网格技术,将不规则的物理区域转换为规则的计算域,给出了贴体坐标系下的二维声波方程及其二阶精度的分部求和(Summation by Parts,SBP)有限差分离散格式，采用Fourier谱分析方法分析了该离散格式的稳定性,得到了贴体网格二维声波方程SBP有限差分方法的稳定性条件。数值实验结果表明：①当时间采样间隔的选取满足稳定性条件时,贴体网格SBP有限差分的数值计算过程是稳定的；②与贴体网格中心差分方法相比，贴体网格SBP有限差分方法的稳定性更好。

关键词:贴体坐标；声波方程；分部求和有限差分；中心差分；稳定性条件

自从1968年ALTERMAN等[1]首次将有限差分方法(FDM)应用于层状介质的弹性波动方程求解问题以来,FDM已经成功地发展成为应用最为广泛的地震波场数值模拟方法之一,并在复杂不均匀介质波场模拟问题上发挥着越来越重要的作用。FDM将求解域划分为规则差分网格,大多用来处理水平地表的模拟问题。在地表起伏不平或者模拟区域不规则的情况下,使用FDM需对求解区域不规则的边界进行阶梯状近似,会在阶梯状网格的角点处产生虚假的散射和绕射,从而影响波场模拟的精度[2-3]。

有限元、边界元等方法适用于不规则区域的地震波场数值模拟。其中有限元法处理不规则地表问题比较方便,能有效地模拟起伏地表情况下的地震波传播,但模拟效率低,精度不高,对机器内存需求也较大。与有限差分方法相比,当二者精度相同时,有限元法更加费时[4-7]。边界积分或边界元法适用于特定形状下的地震波传播,但不适用于地表速度变化较大的情况[8]。相比而言,有限差分法计算效率较高,易于编程和并行运算,并且能够很好地处理各种强不均匀介质问题,因此仍然是解决地震波场数值模拟问题最有效的方法。

贴体坐标技术的提出为有限差分法处理不规则区域问题开辟了新的局面[9-13]。20世纪80年代初期,贴体网格开始用于求解不规则区域的物理问题,并逐渐成为最主要的数值方法之一。TESSMER等[2]基于坐标变换的方法将起伏地表下的曲线网格映射到水平地表下的矩形网格,并使用伪谱法实现了不规则区域中二维弹性波场的数值模拟。HESTHOLM等[4]基于纵向坐标变换,使用高阶交错网格有限差分算子实现了二维起伏地表下的弹性波场数值模拟。1998年,HESTHOLM等[14]将此方法扩展到三维情形,给出了所能模拟的起伏地表最大起伏程度。2003年,HESTHOLM[15]针对不同的dz/dx(z方向和x方向空间采样间隔比值)和纵横波速度比值进行了基于映射的弹性波场数值模拟,并通过实验给出了达到长时间稳定的dz/dx取值范围,但未进行理论上的推导,也未讨论时间采样间隔的影响。董良国[16]在横波品质因子Q值的基础上,借助纵向坐标变换,利用交错网格高阶差分方法对起伏地表情况下的弹性波传播进行了数值模拟。针对规则网格中二阶形式的弹性波方程和自由边界条件,NILSSON等[17]给出了二阶精度的分部求和(SBP)差分格式,讨论了非均匀介质中该差分算法的稳定性条件。APPELÖ等[18]将NILSSON等[17]研究的方法扩展到曲线坐标系,通过构造曲线网格中的二阶SBP离散格式,实现了不规则区域的弹性波模拟,但未涉及曲线坐标系中相应的稳定性条件。TARRASS等[19]借鉴空气声学中的非中心差分算子,使用高阶的空间和时间优化算子模拟起伏地表下的波场传播,给出了差分格式的稳定性条件,但是该方法的网格剖分基于坐标映射,导致该方法的稳定性在一定程度上依赖于地形的起伏,当地形较陡时,该方法稳定性变差。LAN等[8]将APPELÖ等[18]研究的方法扩展到三维非均质各向异性介质,采用曲线坐标离散并求解垂直对称轴横向各向同性(VTI)介质中的弹性波方程和自由边界条件,实现了起伏地表下VTI介质中地震波场的显式有限差分模拟。此后,LAN等[20]采用类似的方法实现了起伏地表下水平对称轴横向各向同性(HTI)介质中地震波场的显式有限差分模拟。刘一峰等[21]借助贴体网格技术,研究了曲线坐标系中程函方程的求解方法。唐文等[22]通过坐标变换,实现了起伏地表二阶弹性波方程的地震波场数值模拟,研究了起伏地表下的自由边界条件,定性地比较了采用不同自由边界条件时模拟算法的稳定性,但未定量给出差分格式的稳定性条件。

本文基于贴体坐标的概念,首先给出贴体网格中的二维声波方程以及完全匹配层(PML)吸收边界条件；然后采用二阶精度的SBP有限差分对贴体网格的声波方程进行离散,推导了该离散格式的稳定性条件；最后通过数值模拟验证该稳定性条件的正确性,并通过与贴体网格中心差分方法对比,显示贴体网格SBP有限差分方法在稳定性方面的优势。

1技术方法

1.1贴体坐标系中二维声波方程、PML及其离散格式

1.1.1贴体坐标系的生成

贴体坐标系是由物理区域的边界点坐标经过数值计算生成的坐标系,能够很好地与边界形状相适应。贴体网格的生成可以看作是一种坐标变换,它把物理平面上的不规则区域变换为计算平面上的规则区域。一般采用偏微分方程法实现贴体坐标变换,变换关系为[9-10]:

(1)

(2)

其中,

(3)

1.1.2贴体坐标系中的声波方程、PML和中心有限差分算子

经过坐标变换,贴体坐标系中的二维声波方程可以表示为:

(4)

其中,u为声压场,v为声波的传播速度,t为时间变量。

为了消除正演模拟过程中的人工边界反射,在贴体坐标系中引入了PML边界条件,经过一系列的推导,得到方程(4)对应的时间域分裂式PML匹配方程:

(5)

其中,u=u1+u2+u3+u4+u5,u1,u2,…,u5为分裂的声压场；dq,dr代表PML区域中q,r方向的衰减函数；“*”表示时间褶积。(4)式和(5)式中的时间导数和空间导数均采用二阶中心差分,即:

(6)

将(6)式代入方程(4)和方程(5)中即可得到贴体坐标系中二维声波方程和PML匹配方程的二阶中心差分离散格式。

1.1.3贴体坐标系中的SBP有限差分算子

地下介质的强非均质性使得介质参数在远小于地震波波长的空间范围内变化巨大,这种变化在计算区域的网格中更加剧烈[17]。为了确保计算的稳定性,必须研究合适的数值方法。1974年,KREISS等[24]提出了一种稳定的有限差分方法,可以求解连续时间系统中能量守恒的偏微分方程。由于该方法满足SBP性质,因而被称为SBP有限差分方法。

为了方便地使用SBP有限差分方法,我们将贴体坐标系中的二维声波方程写为:

(7)

其中,

(8)

可以证明,方程(7)和方程(4)是等价的。该方程对应的时间域分裂式PML匹配方程可以表示为:

(9)

其中,u=u1+u2+u3。

将(7)式中的空间变量导数项替换为SBP有限差分,时间变量导数项替换为二阶中心差分,可以得到贴体坐标系中二维声波方程的SBP有限差分离散格式:

(10)

其中,D+,D-为标准的向前、向后差分算子,以r方向为例,

(11)

(12)

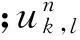
类似地,可以得到PML匹配方程(9)的SBP有限差分离散格式:

(13a)

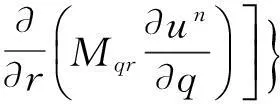
(13b)

(13c)

其中,

(14)

通过能量估计可以证明,该SBP差分格式满足离散能量守恒[17],与传统的中心差分方法相比,具有更好的稳定性,形式也更简洁[25]。

1.2稳定性分析

本节讨论贴体坐标系中二维声波方程的SBP有限差分格式(10)的稳定性条件。常用的有限差分稳定性分析方法是VONNEUMANN等[26]和SJÖGREEN[27]提出的Fourier谱分析方法,该方法适用于常系数初值和带周期边值条件的混合问题,因此假定公式(10)中的介质参数Mqq,Mrr和J为常量。由于

(15)

而在曲线坐标系中坐标线正交的条件是β=0,因此Mqr=0,公式(10)简化为：

(16)

公式(16)中的空间差分算子在Fourier域对应为:

(17)

(18)

经过Fourier变换,公式(16)对应为:

(19)

其中,

(20)

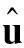
(21)

公式(21)右端的矩阵称为增长矩阵,简记为G。当增长矩阵的谱半径ρ(G)≤1,即G的所有特征值的模小于等于1时,差分格式稳定。矩阵G的特征值λ满足的特征方程为:

(22)

特征方程的解为:

(23)

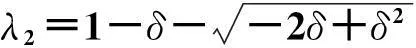
如果0≤δ≤2,判别式的值为负值或0,特征方程有一对复共轭的根:

(24)

根的模满足

(25)

此时稳定的必要条件得到满足。进一步分析0≤δ≤2时对应的时间采样间隔:

(26)

(27)

稳定性条件为:

(28)

值得注意的是,受Fourier谱分析方法本身的限制,针对贴体网格声波方程SBP有限差分离散格式的稳定性分析较为粗略,并带有一定的近似。能量法可以精确地分析稳定性问题,但是能量法中谱半径的求解是个难题,即使在笛卡尔坐标系中也无法得到其解析解[27]。因此,Fourier谱分析方法仍不失为贴体网格中声波方程SBP有限差分格式稳定性分析的一种有效手段。

2数值模拟

为了验证贴体坐标系中二维声波方程SBP有限差分格式的稳定性条件,即公式(28)的正确性,选取不同的时间采样间隔进行正演模拟,通过与二阶中心差分格式的贴体坐标声波方程正演模拟结果进行对比,显示出贴体网格SBP有限差分方法在稳定性方面的优势。鉴于本文主要是为了验证差分格式的稳定性,因此在正演模拟过程中,模型的四周均采用了PML吸收边界条件。

为了简单起见,设计带有正弦函数起伏地表的二维均匀模型,如图1所示。模型大小为4000m×3000m,介质的速度为2500m/s。该模型的地表可用正弦函数y=Asin(2πx/T)表示,其中,A=-60m,T=520m,即该模型地表的起伏周期为520m,相对最大高差为120m。震源采用主频为20Hz的Ricker子波,震源位置坐标为(2080m,36m)。正演模拟采用的空间采样间隔为Δq=Δr=4m。

图1　正弦函数起伏地表模型

首先利用(28)式计算出该模型SBP有限差分格式的稳定性条件为Δt≤0.93ms。为了对比验证该稳定性条件,分别选取时间采样间隔Δt=0.90ms以及Δt=1.00ms进行正演模拟,记录长度为6s。图2a和图2b分别为时间采样间隔为0.90ms和1.00ms时的模拟地震记录,可以看出,在满足稳定性条件的情况下,利用贴体网格SBP有限差分方法可以得到清晰的直达波记录(图2a),而在时间采样间隔不满足稳定性条件时,出现数值结果的溢出(图2b)。图2c和图2d分别是从图2a和图2b两个地震记录中抽取的5个地震道,抽取的位置如图2a和图2b中倒三角所示。

从抽取的单道记录中可以得出相同的结论:当时间采样间隔为0.90ms时,满足稳定性条件,此时贴体网格SBP有限差分方法模拟的整个记录是稳定的;而当时间采样间隔为1.00ms时,超出了稳定性条件的范围,此时贴体网格SBP有限差分方法的模拟结果不稳定,造成数值结果溢出,波动方程的数值求解失败。

图3a和图3b分别为贴体网格的SBP有限差分方法和中心有限差分方法正演模拟得到的地震记录对比,两种方法的时间采样间隔均为Δt=0.93ms。正演模拟记录时间长度为30s,为了美观,只显示到23s左右。图3c和图3d分别是从图3a和图3b两个地震记录中抽取的3个地震道,抽取的位置如图3a和图3b中倒三角所示。从图3 可以看出,在相同时间采样间隔的情况下,贴体网格SBP有限差分方法和中心有限差分方法均可以得到清晰的直达波记录,但中心有限差分方法在18s左右开始出现不稳定的数值,并且这种不稳定性随着时间的推移越来越严重。从抽取的单道记录中可以得出相同的结论:贴体网格SBP有限差分方法模拟的整个记录都是稳定的,而中心有限差分方法模拟的记录在后期出现不稳定,数值结果溢出。

图2　时间采样间隔为0.90ms(a)和1.00ms(b)正演模拟的地震记录及其5个地震道(c)和(d)

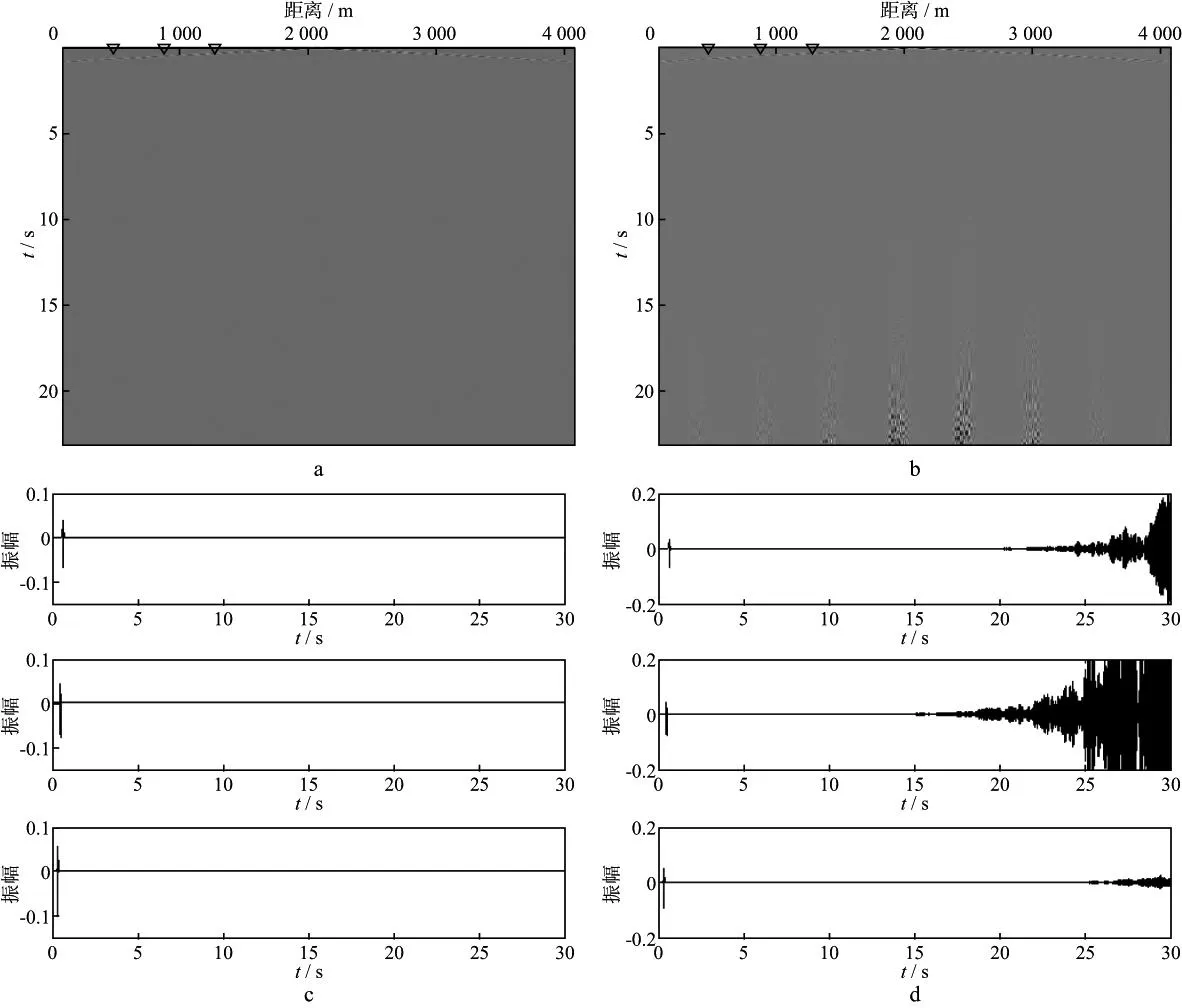
图3　贴体网格SBP有限差分法(a)和中心差分法(b)正演模拟的地震记录及其3个地震道(c)和(d)

3结束语

本文针对贴体坐标系中声波方程的SBP有限差分离散格式,采用Fourier谱分析方法讨论了该离散格式的稳定性条件，通过对起伏地表均匀介质模型选取不同的时间采样间隔进行正演模拟对比,验证了该稳定性条件的正确性。与贴体网格中心差分方法相比,贴体网格SBP有限差分方法更加稳定,适用于求解不规则区域的波动方程。

本文的SBP有限差分算子仅限于二阶精度,贴体坐标系中声波方程的高精度SBP有限差分算法及对应的稳定性条件将是我们今后研究的重点。

参考文献

[1]ALTERMAN Z,KARAL F C.Propagation of elastic waves in layered media by finite difference methods[J].Bulletin of the Seismological Society of America,1968,58(1):367-398

[2]TESSMER E,KOSLOFF D,BEHLE A.Elastic wave propagation simulation in the presence of surface topography[J].Geophysical Journal International,1992,108(2):621-632

[3]ZHANG W,CHEN X F.Traction image method for irregular free surface boundaries in finite difference seismic wave simulation[J].Geophysical Journal International,2006,167(1):337-353

[4]HESTHOLM S,RUUD B.2D finite-difference elastic wave modeling including surface topography[J].Geophysical Prospecting,1994,42(5):371-390

[5]KOMATITSCH D,TROMP J.Introduction to the spectral element method for three-dimensional seismic wave propagation[J].Geophysical Journal International,1999,139(3):806-822

[6]BROSSIER R,VIRIEUX J,OPERTO S.Parsimonious finite-volume frequency-domain method for 2D P-SV-wave modeling[J].Geophysical Journal International,2008,175(2):541-559

[7]LIU T,HU T Y,SEN M K,et al.A hybrid scheme for seismic modelling based on Galerkin method[J].Geophysical Journal International,2011,186(3):1165-1178

[8]LAN H Q,ZHANG Z J.Three-dimensional wave-field simulation in heterogeneous transversely isotropic medium with irregular free surface[J].Bulletin of the Seismological Society of America,2011,101(3):1354-1370

[9]THOMPSON J F,THAMES F C,MASTIN C W.Automatic numerical generation of body-fitted curve linear coordinate system for field containing any number of arbitrary two-dimensional bodies[J].Journal of Computational Physics,1974,15(3):299-319

[10]THOMPSON J F,THAMES F C,MASTIN C W.TOMCAT-A code for numerical generation of boundary-fitted curvilinear coordinate systems on fields containing any number of arbitrary two-dimensional bodies[J].Journal of Computational Physics,1977,24(3):274-302

[11]THOMPSON J F,WARSI Z U A,MASTIN C W.Numerical grid generation:foundations and applications[M].New York:Elsevier North-Holland,1985:1-3,95

[12]LAKNER M,PLAZL I.The finite differences method for solving systems on irregular shapes[J].Computers and Chemical Engineering,2008,32(12):2891-2896

[13]KAUL U K.Three-dimensional elliptic grid generation with fully automatic boundary constraints[J].Journal of Computational Physics,2010,229(17):5966-5979

[14]HESTHOLM S,RUUD B.3-D finite-difference elastic wave modeling including surface topography[J].Geophysics,1998,63(2):613-622

[15]HESTHOLM S.Elastic wave modeling with free surfaces:stability of long simulations[J].Geophysics,2003,68(1):314-321

[16]董良国.复杂地表条件下地震波传播数值模拟[J].勘探地球物理进展,2005,28(3):187-194

DONG L G.Numerical simulation of seismic wave propagation under complex near surface conditions[J].Progress in Exploration Geophysics,2005,28(3):187-194

[17]NILSSON S,PETERSSON N A,SJÖGREEN B,et al.Stable difference approximations for the elastic wave equation in second order formulation[J].SIAM Journal on Numerical Analysis,2007,45(5):1902-1936

[18]APPELÖ D,PETERSSON N A.A stable finite difference method for the elastic wave equation on complex geometries with free surfaces[J].Communications in Computational Physics,2009,5(1):84-107

[19]TARRASS I,GIRAUD L,THORE P.New curvilinear scheme for elastic wave propagation in presence of curved topography[J].Geophysical Prospecting,2011,59(5):889-906

[20]LAN H Q,ZHANG Z J.Seismic wavefield modeling in media with fluid-filled fractures and surface topography[J].Applied Geophysics,2012,9(3):301-312

[21]刘一峰,兰海强.曲线坐标系程函方程的求解方法研究[J].地球物理学报,2012,55(6):2014-2026

LIU Y F,LAN H Q.Study on the numerical solutions of the eikonal equation in curvilinear coordinate system[J].Chinese Journal of Geophysics,2012,55(6):2014-2026

[22]唐文,王尚旭,袁三一.起伏地表二阶弹性波方程差分策略稳定性分析[J].石油物探,2013,52(5):457-463

TANG W,WANG S X,YUAN S Y.Stability analysis of differential strategy for rugged topography by second-order elastic wave equation based on coordinate transformation[J].Geophysical Prospecting for Petroleum,2013,52(5):457-463

[23]WEI W L,JIN Z Q.Numerical solution for unsteady 2-D flow using the transformed shallow water equations[J].Journal of Hydrodynamics,1995,7(3):65-71

[24]KREISS H O,SCHERER G.Finite element and finite difference methods for hyperbolic partial differential equations[M].New York:Academic Press,1974:195-212

[25]DIENER P,DORBAND E N,SCHNETTER E,et al.Optimized high-order derivative and dissipation operators satisfying summation by parts,and applications in three-dimensional multi-block evolutions[J].Journal of Scientific Computing,2007,32(1):109-145

[26]VON NEUMANN J,RICHTMYER R D.A method for the numerical calculation of hydrodynamic shocks[J].Journal of Applied Physics,1950,21(3):232-237

[27]SJÖGREEN B,PETERSSON N A.A fourth order accurate finite difference scheme for the elastic wave equation in second order formulation[J].Journal of Scientific Computing,2012,52(1):17-48

(编辑:戴春秋)

Stability analysis of SBP finite difference scheme for two-dimensional acoustic wave equation in boundary-conforming grids

WANG Ying1,ZHOU Hui1,SHENG Shanbo2

(1.StateKeyLaboratoryofPetroleumResourceandProspecting,CNPCKeyLabofGeophysicalProspecting,ChinaUniversityofPetroleum,Beijing102249,China;2.ChinaNationalOil&GasExplorationandDevelopmentCorporation,Beijing100034,China)

Abstract:Traditionally,finite difference method is widely used as a fast and accurate method for numerical simulation and migration of wave equation.However,finite difference method faces obstacles when there are surface topography and irregular interfaces.The staircase approximations caused by regular grids influence the accuracy of finite difference method.Boundary-conforming grids by elliptic method offer an optimal alternative for finite difference wavefield simulation in irregular regions.By such grids,the calculations of spatial derivatives are transformed by a chain rule into those in the regular computational space,where traditional finite difference schemes are still applicable.The two-dimensional acoustic wave equation is reformulated in boundary-conforming grids.The Summation-by-Parts (SBP) finite difference scheme with second order accuracy is used for discretization.The stability of the discretization formula is discussed by Fourier spectral method to obtain the stability condition of the SBP finite difference scheme for two-dimensional acoustic wave equation in boundary-conforming grids.A numerical test shows that the accuracy and effectiveness can be guaranteed by reasonably choosing the parameters in numerical simulation,such as the temporal and spatial intervals.Comparisons between the numerical simulations of SBP and central finite difference method in boundary-conforming grids are performed,which shows that SBP finite difference scheme is more stable.

Keywords:boundary-conforming grids,acoustic wave equation,SBP finite difference,central finite difference,stability condition

文章编号:1000-1441(2016)01-0033-08

DOI:10.3969/j.issn.1000-1441.2016.01.005

中图分类号:P631

文献标识码:A

基金项目:国家重点基础研究发展计划(973计划)(2013CB228603)、国家自然科学基金(41174119)和中石油物探新方法新技术研究(2014A-3609)项目共同资助。

作者简介:王颖(1987—),女,博士在读,主要从事地震数据处理新方法研究。通讯作者:周辉(1966—),男,教授,博士生导师,主要从事地震正演模拟、波形反演、偏移成像研究工作。

收稿日期:2015-06-03;改回日期:2015-08-10。

王颖,周辉,盛善波.贴体坐标系二维声波方程SBP有限差分法的稳定性分析[J].石油物探,2016,55(1):-40

WANG Ying,ZHOU Hui,SHENG Shanbo.Stability analysis of SBP finite difference scheme for two-dimensional acoustic wave equation in boundary-conforming grids[J].Geophysical Prospecting for Petroleum,2016,55(1):-40

This research is financially supported by the National Key Basic Research Program of China (973 Program)(Grant No.2013CB228603),the National Science Foundation of China (Grant No.41174119) and CNPC Geophysical Exploration New Technology Research Program (Grant No.2014A-3609).