仓储系统伸缩臂的结构优化研究*

陈俊明，刘　琼，廖源泉

(南华大学机械工程学院，湖南衡阳421001)



仓储系统伸缩臂的结构优化研究*

陈俊明，刘琼，廖源泉

(南华大学机械工程学院，湖南衡阳421001)

摘要：对仓储系统伸缩臂的结构进行了优化,优化的目的是减少伸缩臂的截面面积,从而降低制造成本。建立了伸缩臂优化数学模型,采用改进粒子群算法对该数学模型进行计算寻求截面面积的最小值,结果表明:相比基本粒子群算法，改进粒子群算法能够有效避免算法陷入局部最优解，优化效果更好。将伸缩臂三维模型导入有限元软件中进行结构静力分析与验证,结果表明优化后的伸缩臂结构力学性能满足工况要求。

关键词：仓储系统伸缩臂结构优化粒子群算法有限元分析

0引言

立体仓库已经成为现代仓储的发展方向。伸缩臂因其结构紧凑，存取料灵活的优点，满足现代智能化仓储系统空间利用率高的特点，已经成为现代仓储系统中接送料机构的关键部件。其性能的优劣对整个现代仓储系统的运作效率影响重大，而且现代仓储系统中的伸缩臂多数采用的是齿轮齿条直线差动行程倍增机构[1]，其结构外形相似，通用性较强。目前有较多文献对于大型工程机械伸缩臂结构进行了优化研究，而对现代仓储系统中的伸缩臂结构优化研究还缺乏具体的工程实例。文献[2]针对仓储系统伸缩臂的外观与传动特性进行了设计，文献[3-4]对仓储系统伸缩臂的挠度与强度进行了计算与校核，文献[5]对仓储系统伸缩臂的动力学特性进行了分析，但还没有文献对仓储系统伸缩臂的结构进行优化研究。综上所述对现代仓储系统中的伸缩臂进行优化研究是很有现实意义的。

粒子群算法[6](Particle Swarm Optimization， PSO)是一种典型的群体智能算法，因其简单、易实现，不要求目标函数和约束条件可微，收敛速度快且可调参数较少等优点得到广泛应用，目前已成功应用于复杂系统的参数优化、神经网络权值的训练及求解组合优化问题[7]等许多优化问题中。伸缩臂结构优化问题是多变量多约束的非线性规范问题，由传统的迭代方法进行优化容易使目标函数陷入局部最优，从而难以找到最优解。因此选择粒子群算法对伸缩臂结构进行优化在理论上是可行的。

1伸缩臂结构及工作原理

伸缩臂一般采用齿轮齿条或链轮链条传动的三级直线差动机构，本文伸缩臂采用齿轮齿条传动。其结构简图如图1，伸缩臂主要由上叉、中间叉、固定叉构成，固定叉固定在工作台上，中间叉相对固定叉可以伸出一定距离，上叉安装在中间叉上，相对中间叉可以伸出更远的距离，实现货物的存取。固定叉及上叉两侧装有导向滚轮，能在中间叉两侧的导轨上滑动。其传动原理如图2，固定齿条安装在固定叉上，滚动齿轮安装在中间叉上，从动齿条安装在上叉上，根据相对运动原理，固定齿条与滚动齿轮的节点为二者的速度瞬心，当安装在中间叉上的滚动齿轮相对于固定叉上的固定齿条滚动时，安装在上叉上的从动齿条以两倍于滚动齿轮中心的速度水平移动，这样就在固定叉，中间叉，上叉之间形成了行程倍增的差动传动[8]。这样的结构紧凑，空间利用率高。

图2　齿轮齿条差动机构

2伸缩臂数学模型的建立

伸缩臂货叉外形尺寸：1 000 mm (长) ×194 mm (宽) ×124 mm (高)，工作参数：行程1 000 mm，最大载荷5 000 N。

2.1伸缩臂受力分析[9]

在最大行程下对伸缩臂受力模型进行简化，简化后的受力模型如图3。

图3　伸缩臂力学模型

图中，a、b、c、d、e、f为各支点间尺寸;FA、FB、FC、FD、FE为支点反力;G为货物重量。设W1，W2，W3分别为上叉、中间叉、固定叉的截面系数;I1，I2，I3分别为上叉、中间叉、固定叉的截面惯性矩;E为材料的弹性模量。

2.1.1上叉受力分析

上叉在货物的作用下，在D、E处产生支反力，其受力如图4所示。

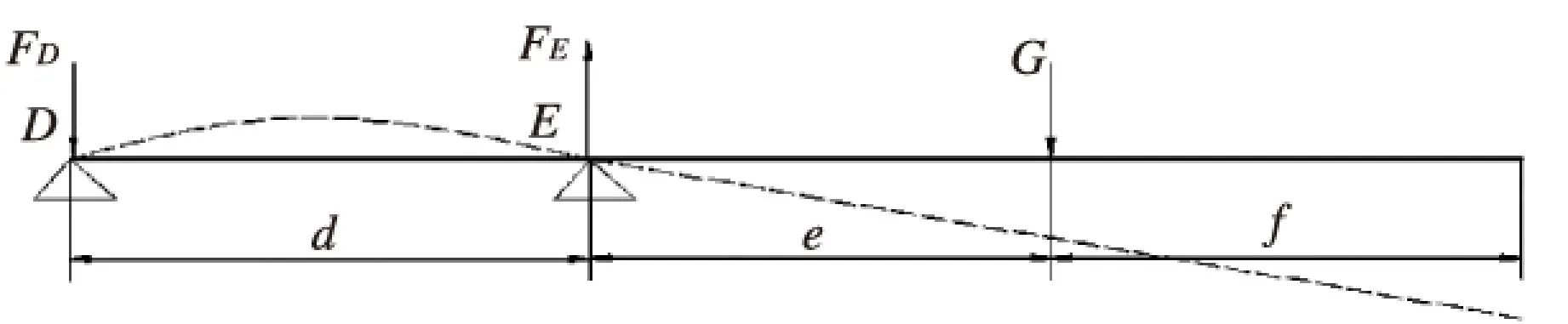
图4　上叉受力简图

由图可得D、E支点反力:

FD=eG/d

(1)

FE=(e+d)G/d

(2)

E点倾角:

θE=-eGd/3EI1

(3)

引起伸缩臂前端挠度：

K1=θE(e+f)=-Ged(e+f)/3EI1

(4)

上叉最大弯矩发生在E点:

ME=-Ge

(5)

上叉最大弯曲应力:

σ1=ME/W1

(6)

2.1.2中间叉受力分析

中间叉受力和变形如图5所示。

图5　中间叉受力简图

如图(a)所示，将C点到伸缩臂前端看作整体，可得B、C支点反力:

FB=(c+d+e)G/b

(7)

FC=G(b+c+d+e)/b

(8)

C点倾角：

θC=-Gb(c+d+e)/3EI2

(9)

引起伸缩臂前端挠度为:

K2=-Gb(c+d+e)(c+d+e+f)/3EI2

(10)

如图(b)所示，设BC段为刚性，C为固定端，把BC段看作刚性，C端为固定端。由FD产生的伸缩臂D点倾角和前端挠度分别为:

θD=eGc2/2EI2d

(11)

K3=eGc2[3(c+d+e+f)-c]/6EI2d

(12)

由FE产生的伸缩臂E点倾角和前端挠度分别为:

θe=-G(d+e)(c+d)2/2EI2d

(13)

K4=-G(e+d)(c+d)2[3(c+d+e+f)-(c+d)]/6EI2d

(14)

中间叉最大弯矩发生在C点或D点，中间叉最大弯曲应力:

σ2=MC/W2或σ2=MD/W2

(15)

2.1.3固定叉受力分析

设C点到伸缩臂前端为不变形部分，固定叉受力如图6所示。

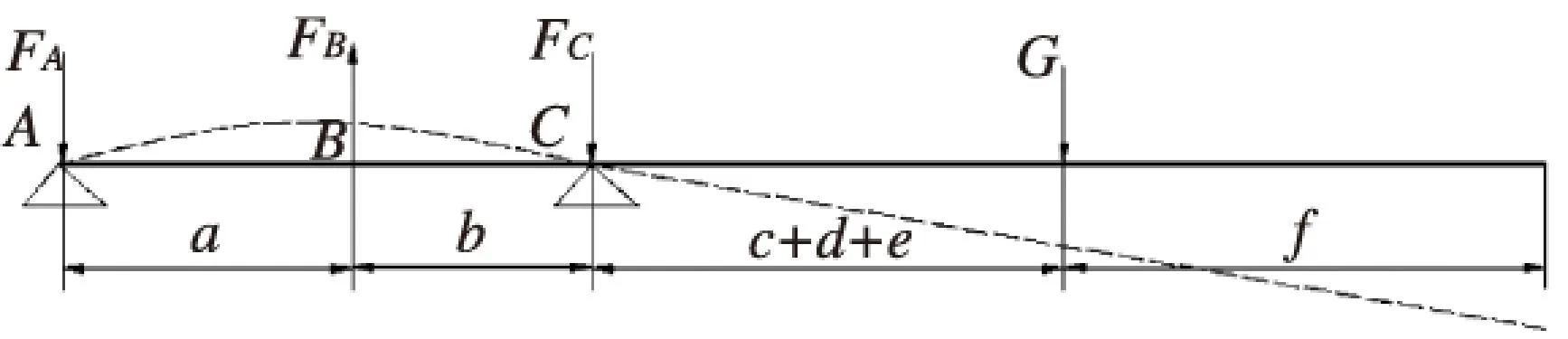
图6　固定叉受力简图

由图可得A点支反力:

FA=(c+d+e)G/(a+b)

(16)

由FB产生C点倾角与前端挠度分别为:

θC=-Gab(c+d+e)(2a+b)/6EI3b(a+b)

(17)

K5=-Gab(c+d+e)(2a+b)(c+d+e+f)/6EI3b(a+b)

(18)

固定叉最大弯矩发生在B点:

MB=-Ga(c+d+e)/(a+b)

(19)

固定叉最大弯曲应力:

σ3=MB/W3

(20)

2.2伸缩臂优化数学模型

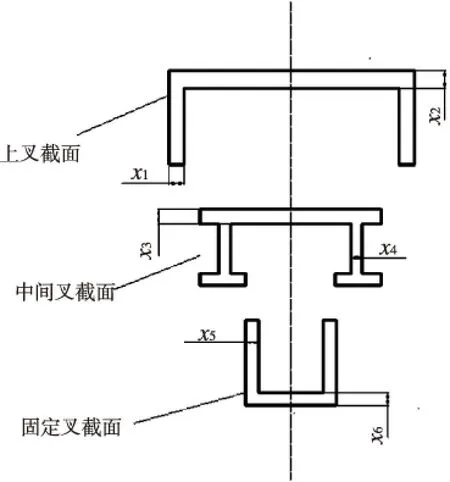
图7　伸缩臂截面简图

以伸缩臂制造经济性为目标，即以伸缩臂重量为目标，由于伸缩臂可以看作等截面梁，因此可以简化为以伸缩臂截面面积为优化目标函数。伸缩臂截面简图如图7所示。

由上到下，伸缩臂截面分为上叉截面，中间叉截面，固定叉截面。x1，x2，…x6为截面厚度，单位为mm。其中i=1，2，3，分别表示上叉，中间叉，固定叉;A，M，W分别表示横截面积，最大弯矩，截面系数。伸缩臂叉取货物的最大挠度一般规定不超过5mm[10]，即[K]=K1+K2+K3+K4+K5≤5mm，伸缩臂许用弯曲应力[σ]为50MPa[4]。为了满足工艺尺寸约束条件，截面厚度尺寸应控制在5mm～20mm之间。以伸缩臂截面面积为目标函数，以截面厚度为设计变量，以伸缩臂挠度，强度等为约束条件建立优化数学模型如下:

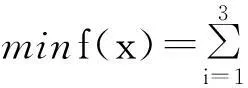
K(x)=K1(x)+K2(x)+K3(x)+K4(x)+K5(x)≤[K]

5≤xj≤20(j=1，2，3…6)

(21)

3伸缩臂结构优化

3.1基本粒子群算法

在PSO算法模型中，每个粒子的状态由两个向量来描述:速度向量表示粒子在搜索空间的运动方向，位置向量表示问题的可行解。粒子通过不断学习自己发现的局部最优解pbest和全局最优解gbest，实现算法的全局最优搜索[6]。基本PSO算法速度与位置更新方程如下：

vij(t+1)=ωvij(t)+c1r1[pbestij(t)-xij(t)+→

←c2r2(gbestj(t)-xij(t))]

(22)

xij(t+1)=xij(t)+vij(t+1)

(23)

式中：vij(t)，xij(t)分别表示粒子i在进化到第t代时的第j维飞行速度分量和位置分量;pbestij(t)表示粒子i在进化到t代时的第j维个体最优位置pbesti分量;gbestj(t)表示进化到t代时整个粒子群最优位置gbest的第j维分量;c1，c2加速因子或学习因子，c1调节粒子飞向自身最优位置的飞行步长，c2调节粒子飞向群体最优位置的飞行步长；r1，r2[0，1]的随机数;ω为惯性权重， 代表粒子先前速度对当前速度的影响，基本PSO算法ω取1。

3.2惯性权重线性递减的改进粒子群算法

ω为惯性权重， 代表粒子先前速度对当前速度的影响，用来调节全局搜索与局部搜索能力。Shi[11]等研究发现，当ω≤0.8时，PSO算法具有较强的局部搜索能力，ω≥1.2时，PSO算法具有较强的全局探索能力。基本PSO算法ω恒为1，不能动态灵活地调节全局搜索与局部搜索能力，不利于粒子群保持多样性，因此容易陷入局部最优解。针对基本PSO算法的这种缺陷，提出一种ω调整策略：在进化过程中，线性减少ω的值，这样可以使算法在进化初期全局探索能力较强，能在较大范围的解空间内搜索，并不断搜索新的区域，在后期逐渐收敛到较好的区域再进行更精细的搜索，以加快收敛速度。这样可以灵活地调节全局搜索与局部搜索能力，有助于保持粒子群的多样性，有效避免了基本PSO算法容易陷入局部最优解的缺陷，并且收敛速度更快。惯性权重线性递减的改进粒子群算法 (AdvancedParticleSwarmOptimization，APSO)的惯性权重更新公式如下：

ω=(ω1-ω2)×(T-t)/T+ω2

(24)

式中：ω1，ω2分别为惯性权重的初始值与终端值；t和T分别为当前进化代数和最大进化代数。

3.3两种粒子群算法优化及比较分析

运行PSOt优化工具箱[12]，粒子数取30，ω1取0.9，ω2取0.4，c1=c2=2，最大进化代数取1 500，算法优化过程如图8所示，图中横坐标为算法进化代数，纵坐标为对应的最优解，左图为基本PSO算法收敛曲线图，在进化初期，曲线下降速度较快，随着进化代数增加，由于基本PSO算法ω恒为1，不能灵活地调节搜索能力，进化到100代以后曲线下降速度缓慢，逐渐陷入局部最优解，最终进化到1 000代左右收敛， 最优解为5 905.44mm2；右图为APSO算法收敛曲线图，在进化初期，全局搜索能力较强，曲线下降速度较快，随着ω值逐渐减少，算法的全局搜索能力下降，局部搜索能力加强，进化到200代以后，曲线下降速度减慢，算法收敛速度加快，进化到600代左右时收敛，最优解为5 767.3mm2。比较可知:APSO算法比基本PSO算法少进化了400代左右，收敛速度更快，并且优化效果更好。

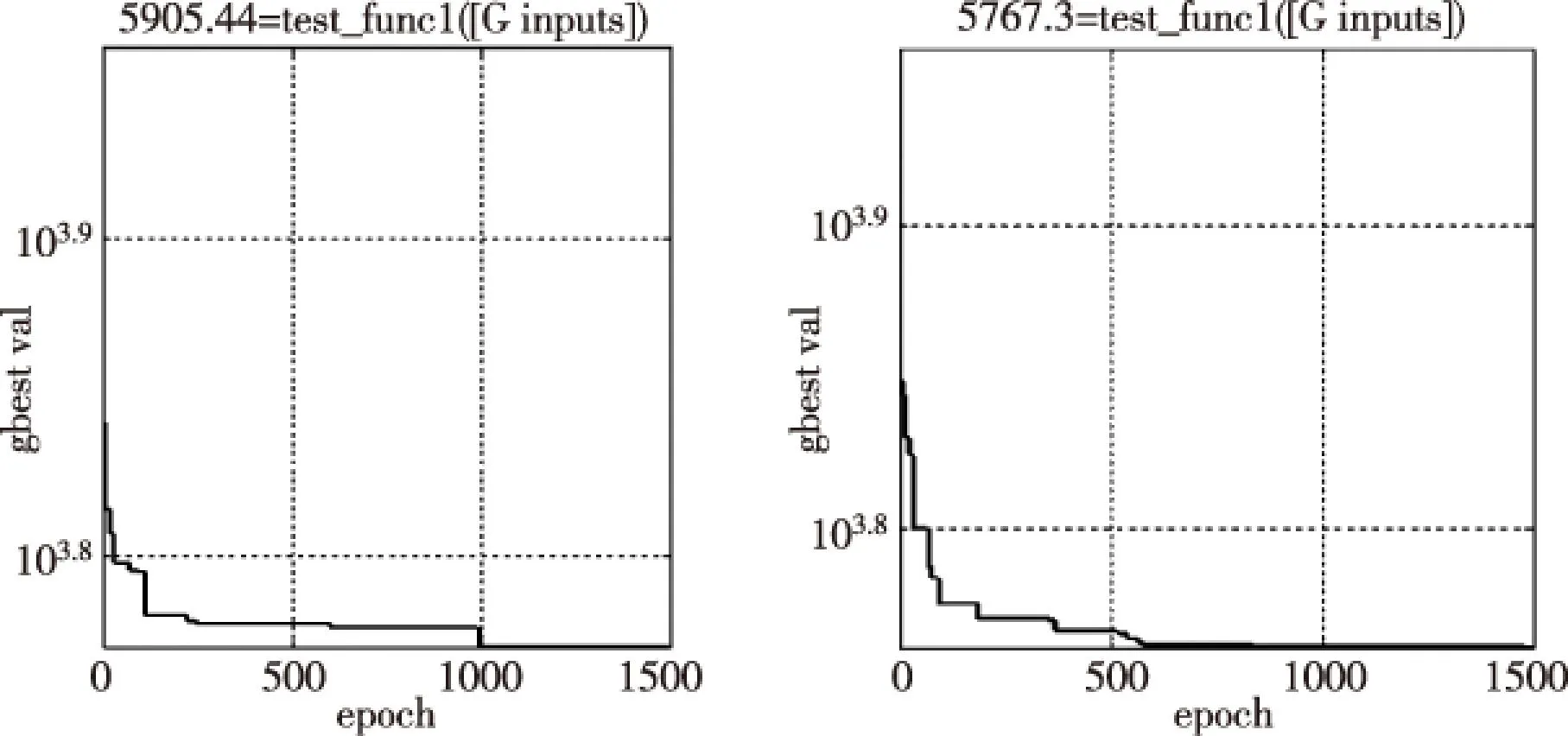
图8　PSO算法与APSO算法收敛曲线图

算法优化结果见表1，由表可知:相对于优化前，两种粒子群算法优化后伸缩臂截面面积都有所减少，APSO算法优化效果尤为明显。根据实际加工要求，对表1中APSO算法优化结果圆整:x1=5，x2=5，x3=8，x4=5，x5=13，x6=7，f(x)=5 801，相比优化前，伸缩臂截面总面积减少了27.6%，即伸缩臂总重量下降了27.6%，优化效果明显。

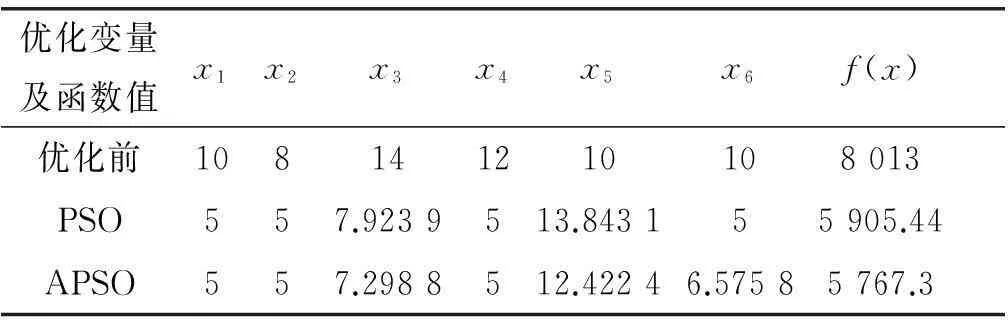
表1　PSO算法与APSO算法优化结果对比

4有限元分析验证

4.1有限元网格的划分

为了减少计算量，将对伸缩臂强度和挠度影响较小的局部结构进行简化，将简化后伸缩臂三维模型导入有限元软件workbench，伸缩臂所用材料为45号钢，设置密度为7 890 kg/m3，泊松比为0.269，弹性模量为210 GPa，屈服强度355 MPa，取安全系数为1.8，即许用应力为197 MPa。采用多区域扫掠方式划分网格，划分后节点总数为148 913，单元总数为88 306，有限元模型如图9所示。

4.2施加载荷及求解

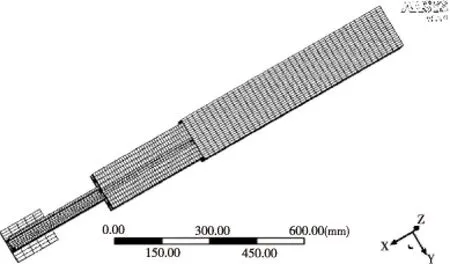
图9　伸缩臂有限元模型

对固定叉底板施加固定约束，因为通常采用一对伸缩臂存取货物，所以每个伸缩臂承受2 500 N的力，均布施加在194 mm×1 000 mm上叉上平面上，即对上叉上平面施加12 887 Pa的均布载荷。求解后得到优化前的伸缩臂Z方向变形(挠度)云图如图10，伸缩臂最大变形发生在伸缩臂的上叉最前端，挠度为0.735 03 mm小于规定值5 mm;等效应力分布云图如图11，最大等效应力发生在固定叉与中间叉接触面附近，大小为112.39 MPa小于许用应力197 MPa，安全裕度较大。

图11　等效应力分布云图

优化后伸缩臂Z方向变形云图如图12，伸缩臂最大变形发生在伸缩臂的上叉最前端，相比优化前有所增加，为2.471 1 mm但小于规定值5 mm;等效应力分布云图如图13，最大等效应力发生在固定叉与中间叉接触面附近及固定叉销轴上，相比优化前也有所增加为157.65 MPa，但小于许用应力197 MPa，满足工况要求。

图13　优化后模型等效应力分布云图

5结语

通过改进ω的调整策略，相比PSO算法，APSO算法能够有效避免算法陷入局部最优解，收敛速度更快，优化效果更好;通过有限元分析验证，优化后的伸缩臂力学性能满足条件，表明改进粒子群算法应用到伸缩臂结构优化研究中是可行的。

在实际工作中，伸缩臂存取货物存在冲击振动大，噪音大，运行不平稳等问题，需要考虑其动态特性。因此进一步研究需要把伸缩臂动力学特性作为约束条件添加到伸缩臂优化数学模型中来。

参考文献

[1]邹雪梅.基于ANSYS的立体库堆垛机货叉建模与分析[D].甘肃:兰州大学，2013.

[2]胡卫宁，卢宗慧，饶金海，等.基于3D设计的新型双伸位货叉[J].制造业自动化，2013，35(8):100-101.

[3]宋章领，沈敏德，薛云娜.堆垛机货叉静态挠度计算[J].起重运输机械，2008(4)41-43.

[4]安晓钢，史胜楠，徐正林.自动化仓库堆垛机货叉强度的分析与计算[J].陕西科技大学学报，2007，25(3):123-125.

[5]孙永吉，张红梅，邹雪娟.堆垛机多级货叉瞬态动力学分析[J].机械设计与制造，2013(4)134-136.

Research on structure optimization of warehousing system’s telescopic boom

CHEN Junming，LIU Qiong，LIAO Yuanquan

Abstract:The structure of warehousing system’s telescopic boom is optimized to reduce the cross-sectional area of telescopic boom, thus reducing the manufacturing cost. The optimization mathematical model of telescopic boom is established, advanced particle swarm optimization algorithm (APSO) is used to calculate the minimum value of cross section area. The results show that: compared with the basic particle swarm optimization algorithm (PSO), APSO can effectively avoid algorithm trapping in partial optimal solution, the optimization effect is better than PSO. The 3D model of telescopic boom is imported into finite element software for structural static analysis and verification. The results indicate that the structural mechanical properties of optimized telescopic boom satisfy the working requests.

Keywords：warehousing system; telescopic boom; structure optimization; particle swarm optimization; finite element analysis

中图分类号：Th146

文献标识码：B

文章编号：1002-6886(2016)01-0014-06