基于Matlab的汽车制动力分配比优化设计

谢欣然

(成都理工大学工程技术学院，四川乐山614000)



基于Matlab的汽车制动力分配比优化设计

谢欣然

(成都理工大学工程技术学院，四川乐山614000)

摘要：对某中型两轴货车进行制动时的受力分析，建立计算两轴汽车前后轴制动利用附着系数φspanφspan的数学模型。以φspanφspan曲线与φ=z直线最接近为优化目标建立多目标优化评价函数，以ECE法规为约束条件，以制动力分配比β为设计变量。运用Matlab优化工具箱进行解算，求出最优点β；运用Matlab计算并输出优化后的φspanφspan曲线与φ=z直线图；β曲线与I曲线图；运用Matlab对制动距离仿真计算,得出采用最优点β的汽车制动性能更好。该优化设计方法对汽车的制动系统设计有一定的指导作用。

关键词:制动强度利用附着系数制动力分配比优化设计Matlab优化工具箱

0引言

汽车是道路交通事故的构成因素之一。汽车造成道路交通事故的最直接原因是技术状况不良。主要表现在汽车制动系统，转向系统，行驶系统，电器系统失效等技术状况不良。汽车制动系统制动性能优劣关系到交通安全。许多道路交通事故与汽车制动性能不良有关。汽车制动性能优劣可以从制动效能，制动效能的恒定性，制动时汽车的方向稳定性来进行评价。具体的评价指标中，制动距离过长，制动减速度不足，汽车制动时侧滑，跑偏或者失去转向能力，都将造成道路交通事故。而两轴汽车前后制动器制动力分配的比例都会影响这些评价指标。同时，在电动汽车，或者混合动力汽车的再生制动和电液制动中，制动力分配的比例也是其稳定性控制算法中的一部分[1]。因此，前后制动器制动力分配比的设计是必须认真考虑的问题。本文以ECE制动法规来确定汽车轴间制动力分配，为汽车制动系统设计提供依据[2]。

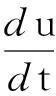
1两轴汽车制动过程受力分析

1.1两轴汽车整车制动受力

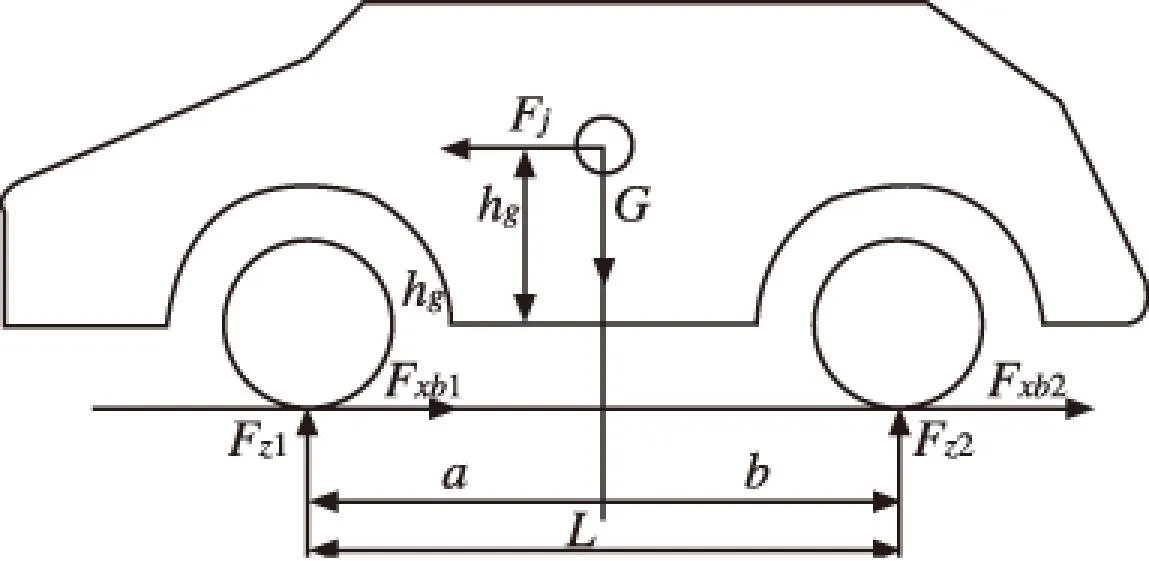
图1　制动时整车受力

在图1中，不考虑汽车的滚动阻力偶矩，空气阻力，旋转质量减速时产生的惯性力偶矩，也不考虑制动时车轮边滚边滑的过程。以前后轮接地点为矩心建立力矩方程[4]，得：

(1)

(2)

式中：FZ1：地面对前轮的法向反作用力(N)；

FZ2：地面对后轮的法向反作用力(N)；

b：汽车质心到后轴中心线的距离(m)；

m：汽车质量(kg)；

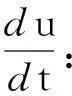
a： 汽车质心到后轴中心线的距离(m)。

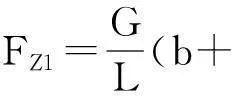
(3)

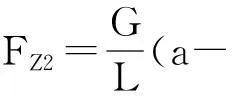
(4)

1.2前后制动器制动力分配比

(5)

Fμ=Fμ1+Fμ2

(6)

式中：β：制动力分配比；

Fμ1：前制动器制动力(N)；

Fμ2：后制动器制动力(N)；

Fμ：汽车总制动力(N)。

1.3利用附着系数

制动时前后轮刚要抱死而还未抱死时,地面制动力达到最大，达到附着力。即使制动器制动力继续增加，地面制动力也不会再增加，此时地面制动力等于制动器制动力。最理想的制动过程实际上就是指制动器制动力始终等于地面制动力[5]。得：

(7)

(8)

(9)

(10)

(11)

(12)

2制动力分配比优化设计

2.1优化变量

以制动力分配比β为优化变量。

2.2优化目标函数

φrφf曲线与z=φ直线越接近，制动强度与利用附着系数就越接近相等，地面的附着条件就发挥得越充分，就越能提高汽车制动性能。根据φrφf计算公式，提高汽车的制动力分配合理程度，即让β取某一个合理值可以得到上述目的。利用最小二乘数学优化方法，让φrφf曲线与z=φ直线之间平方和为最小建立目标函数。考虑满载和空载两种情况。如果只考虑满载情况建立分目标函数，得：

minF1(β)=(φr满-z)2+(φf满-z)2

(13)

只考虑空载情况建立分目标函数，得：

minF2(β)=(φr空-z)2+(φf空-z)2

(14)

如果同时考虑货车空载和满载的情况，这就是一个多目标优化问题。这里采用线性组合法，建立新的目标函数，即建立评价函数[6]。建立评价函数要选择一组加权系数。一般情况下货运平峰期间满载额定率γ ≥0.5~0.6[7]，意味着货运空载概率几乎为0。在这里把货车满载使用频率定为n1，货车空载的使用频率为n2=1-n1。这样可以得到一组加权系数：n1=0%，n2=100%，n1=70%，n2=30%；n1=100%，n2=0%。由此建立评价函数，得：

minF(β)=n1[(φr满-z)2+(φf满-z)2]+(1-n1)[(φr空-z)2+(φf空-z)2]

(15)

2.3约束函数

根据ECE法规，对某中型货车前后轴制动力分配要求如下：对于前后轴φ=0.2~0.8时，z≥0.1+0.85(φ-0.2)；对于最大总质量大于35t的货车，z=0.15~0.3时，每根轴的利用附着系数位于φ=z±0.08两条平行直线之间；z≥0.3时，后轴的利用附着系数满足关系式z≥0.3+0.74(φ-0.78)。据此，可以建立约束：

当0.2≤z≤0.8

当0.15≤z≤0.3

φf-z-0.08≤0

φr-z-0.08≤0

φf-z+0.08≤0

φr-z+0.08≤0

当z≥0.3

2.4计算实例参数

某中型货车，装有前后制动器分开的双管路制动系，制动力分配比为一固定值，其有关参数如表1[8]。制动法规对行车制动性能要求参数见表2、表3[9]。

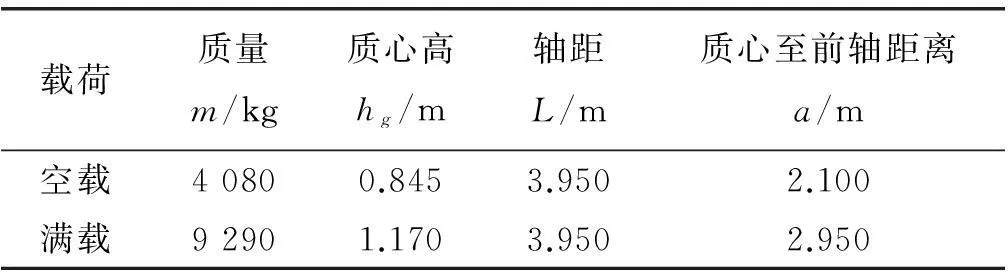
表1　某中型货车有关参数

表2制动法规对制动距离和制动稳定性的要求

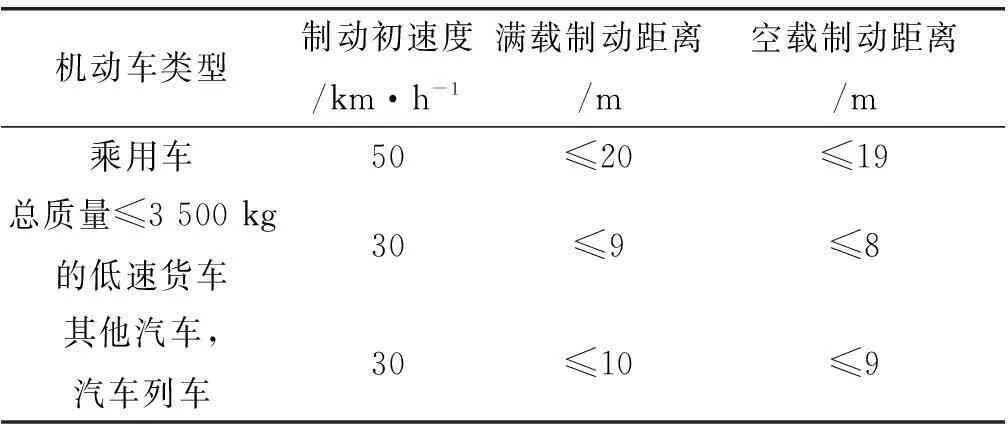
机动车类型制动初速度/km·h-1满载制动距离/m空载制动距离/m乘用车50≤20≤19总质量≤3500kg的低速货车30≤9≤8其他汽车,汽车列车30≤10≤9

表3　制动减速度和制动稳定性的要求

2.5Matlab优化工具箱

根据上述的数学模型及参数，运用Matlab优化工具箱中的fmincon函数进行优化计算。该函数可用于多变量有约束非线性函数最小化的解算。求解得出：

n1=0%时，最优值0.341 9，最优点0.509 0。

n1=70%时，最优值0.278 1，最优点0.484 9。

n1=100%时，最优值0.081 8，最优点为0.431 2。

3优化计算结果分析

3.1对优化后最优解的分析

根据上述，货车运用过程中要尽量避免空载。满载即n1=100%时， 得到的最优值即目标值最小，从而使φ曲线和z直线最为接近。该中型货车越接近满载，优化点的值越小，即β值越小。这表明满载时前轴分配得到的制动器制动力小，前轮比后轮先抱死，这是一种稳定工况。

3.2对优化后优化点对应的同步附着系数分析

计算出β=0.431 2时满载情况下同步附着系数，得：

(16)

代入满载时的中型货车参数，可得：

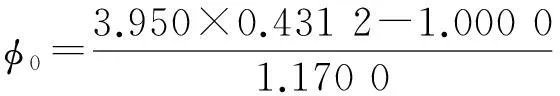
从满载优化最优点计算得出的同步附着系数可以看出，满载时同步附着系数为0.601 2。由于在绝大部分路面上，都是φ≤φ0。制动时前轮先抱死，这是一种稳定工况。

3.3对φrφf曲线与φ=z直线图以及β曲线与I曲线图的分析

由利用附着系数与制动强度曲线图可得，前后轴φrφf曲线满足ECE法规。

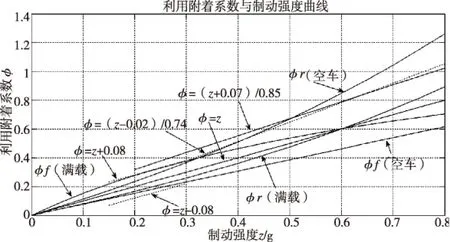
图2　利用附着系数与制动强度曲线

根据图3，满载时，该型货车的β曲线有一部分在I曲线之上，在这个范围内，前轮先抱死，该工况为稳定工况。

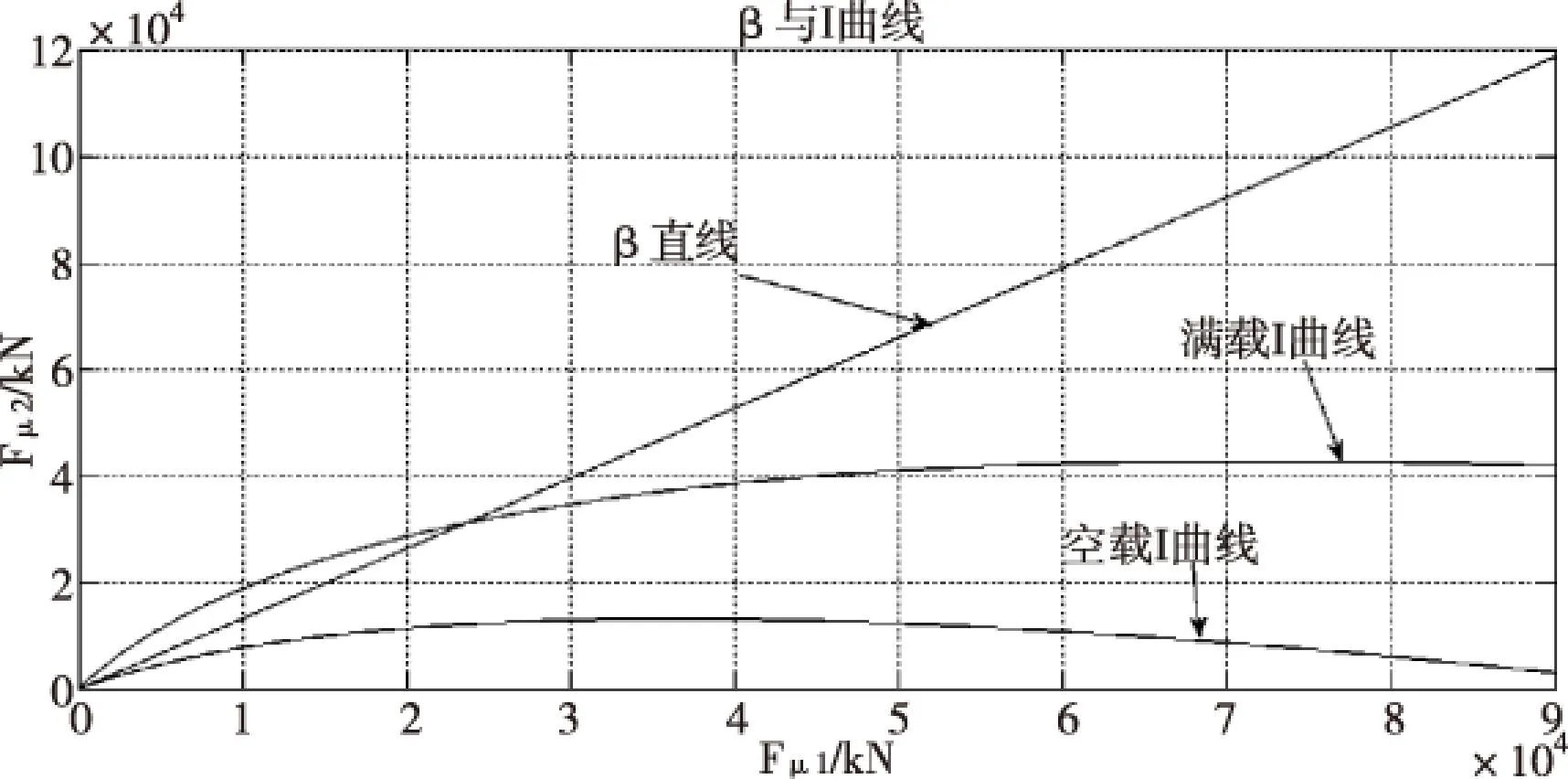
图3　β与I曲线

3.4对优化后制动距离的分析

制动距离是制动效能的评定指标，表3是制动法规对汽车制动性能指标的要求。设定地面附着系数为0.8，当β为最优解0.431 2时，满载制动距离为8.11 m，制动减速度为7.26 m/s2。完全满足制动法规的要求。

4总结

根据本文第3小节的分析，提出的制动力分配比优化设计的数学模型能够求出汽车不同装载工况下的最佳制动力分配比。并且求出的制动力分配比能够满足制动法规对汽车制动性能的要求。

对于制动力分配比恒定的汽车，要让汽车在制动时处于稳定工况，避免道路交通事故的发生，选择合理的制动力分配比尤为重要。运用本文提出的制动力分配比优化设计方法能够解算出合理的制动力分配比并能满足制动法规对汽车制动性能的要求。因此，该优化设计方法对汽车制动系设计有一定的指导意义。

参考文献

[1]Kim, Donghyun; Kim, Chulsoo; Hwang, Sung-Ho; Kim, Hyunsoo. Hardware in the loop simulation of vehicle stability control using regenerative braking and electro[C]//International Federation of Automatic Control. Proceedings of the 17th IFAC World Congress,2008.COEX,Korea,South:Chung,Myung Jin;Misra,Pradeep,2008:5664-5669.

[2]张立军，朱博，贾元雷.依ECE法规进行汽车制动力分配新方法[J].辽宁工程技术大学学报,2005,24(2):266-277.

[3]M Miatluk，Z kaminski，J Czaban.A method of selection of braking forces distribution in a one unit vehicle[EB/OL].http://www.pan-ol.lublin.pl/wydawnictwa/TMot4/Miatluk.pdf.

[4]王亚晴，张代胜，沈国清.汽车制动力分配比的优化设计与仿真计算[J].合肥工业大学学报,2005,28(11):1394-1398.

[5]雷雨成.汽车系统动力学及仿真[M].北京:国防工业出版社,1997：88-89.

[6]张永恒.工程优化设计与MATLAB实现[M].北京:清华大学出版社,2011:172-173.

[7]陈焕江.汽车运用基础[M].北京:机械工业出版社,2014:119-120.

[8]余志生.汽车理论[M].北京:机械工业出版社,2012.

[9]中国国家标准化委员会.机动车运行安全技术条件：GB7258-2004[S].中国标准出版社，2004.

Automobile braking force distribution ratio optimization design based on Matlab

XIE Xinran

Abstract:Through analyzing the braking force of two axis medium van, a mathematical model using attachment coefficient φspanφspanis set up. In order to make φspanφspancurve come closest to φ=z linear, a multi-objective optimization evaluation function is established with ECE regulations as the constraint conditions, and braking force distribution ratio β as the design variable. The optimal point β is worked out employing the Matlab optimization toolbox. Optimized φspanφspancurve，φ=z linear graph，βcurve, and I curve graph are worked out using Matlab. The result shows that, the automobile with optimal β worked out by means of Matlab simulation to calculate the braking distance has better braking efficiency. The optimization method can provide some reference for future design of automobile braking system.

Keywords:braking force; using the adhesion coefficient; braking force distribution ratio; optimization design; Matlab optimization toolbox

收稿日期：2015-08-03

作者简介：谢欣然，男，硕士，工程师，主要从事汽车品质，结构及智能控制方面的研究工作。

中图分类号：TH122

文献标识码：A

文章编号：1002-6886(2016)01-0010-04