一题一课：从基础知识走向数学思想——以“函数视角下的一元二次方程”专题复习为例

☉江苏省苏州市高新区第一中学　蔡映红



一题一课：从基础知识走向数学思想——以“函数视角下的一元二次方程”专题复习为例

☉江苏省苏州市高新区第一中学蔡映红

临近中考，教师教和学生学的时间都非常紧.要想在短期内提升学生的认知水平，教师就必须从“茫茫题海”中精挑细选，选择出合适的题目作为例题原型，通过适度改编呈现出符合学生认知需求和认知规律的教学活动.在二轮复习中，笔者所在的九年级备课组就进行了这样的尝试.我们采用“一题一课”的形式选择和设计例题，以一道综合性较强的例题承载多种基础知识，教学过程就是由基础知识的梳理开始，并逐步过渡到数学思想方法的归纳提升.在“一题一课”实施过程中，取得了一定的成效，当然也存在着这样那样的问题.现结合“函数视角下的一元二次方程”专题复习课的例题教学谈谈笔者的做法及思考，希望对您有所帮助.

一、例题分析

例题关于x的一元二次方程mx2-（4m+1）x+3m+3= 0的两实根分别为x1，x2，n=x1-x2-2，设A（1，a），B（b，2）两点在动点P（m，n）所形成的曲线上，求直线AB的解析式.

简析：本题以一元二次方程为载体，将代数式化简与待定系数法融入其中，考查了一元二次方程的解法（根与系数的关系）、代数式的化简、待定系数法、二元一次方程（组）的解法等知识点，涉及分类讨论、模型、化归等数学思想，这些知识都是初中学段的核心知识.这些知识点的组合，自然合理，是学生认知的自然延伸.解题时，应紧扣一元二次方程的基础知识和代数式的恒等变形，充分应用分类讨论思想、模型思想、数形结合思想，力求将函数问题化归为代数问题.本题的条件环环相扣，紧密链接，抓住了函数问题与代数知识的联系，有效拓展了学生的思维空间，提高对知识的迁移与应用能力，对日常教学有很好的指导与引领作用.

二、教学简录及分析

1.审题指导

教师呈现例题，让学生认真读题，将重要的条件画下来，并思考这些条件在解题中有什么作用.

（学生读题，并在试题上做标记）

学生1：我标记的是“一元二次方程mx2-（4m+1）x+ 3m+3=0的两个实数根分别为x1，x2”.

教师：是的，这个一元二次方程就是这道试题的背景，在这个背景之上又生成了哪些条件呢？

学生2：两个实数根分别为x1，x2；n=x1-x2-2.

学生3：动点P（m，n）形成的曲线；点A（1，a），B（b，2）在曲线上.

教师：要我们求什么呢？

学生（齐）：直线AB的解析式.（教师板书）

简析：直接从题目中抽取条件和结论是学生审题的第一步，也是最关键的一步.教师让学生初读例题，并适当标记，意在培养学生获取题目信息的能力和习惯.

2.思路分析

教师：题目中是否有隐性条件呢？

学生4：点P（m，n）在运动过程中形成了曲线，所以，纵坐标n和横坐标m之间具备函数关系.

教师：抓住哪些条件可以让它“现身”呢？

学生5：一元二次方程mx2-（4m+1）x+3m+3=0和n= x1-x2-2.（板书）

教师：怎么做？

学生6：我想直接解这个方程，求出x1，x2，再代入到n=x1-x2-2中就行了.

教师：怎么解这个方程呢？

学生7：用求根公式求出x1，x2.

教师：有其他求法吗？

学生8：因式分解法.

教师：非常棒！告诉老师你的答案.

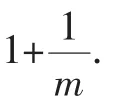
学生9：老师，根据条件“n=x1-x2-2”，完全可以不解这个方程，用根与系数的关系求解.

教师：好的，你说说看！

教师：看来利用根与系数的关系，也可以将n与m关联起来.题目中还有其他隐含条件吗？

学生10：“A（1，a），B（b，2）两点在动点P（m，n）所形成的曲线上”，告诉我们“当m=1时，n=a；当m=b时，n=2”.

教师：这对我们解题有用吗？

学生11：根据这个条件我们可以求出a、b的值，这样就得到了点A、B的坐标了！

教师：根据刚刚的分析，该从哪里下手呢？

学生12：点A、B的坐标（板书）.

教师：怎么求这两个点的坐标呢？

学生13：抓住“当m=1时，n=a；当m=b时，n=2”这个隐含条件，利用我们得出的n与m的函数关系式，就行了！（教师板书：n与m的函数关系式）

教师：很好，这样一来，又回到了我们刚才的思路上来了.你们得出这道试题的解题思路了吗？

（画出箭头，完成图1中的板书）

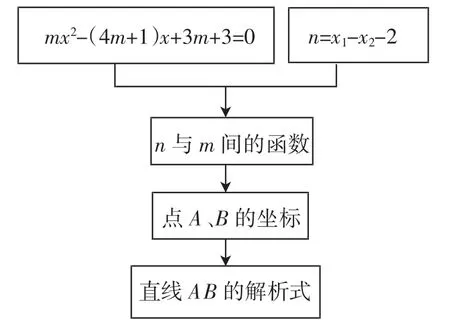
图1

教师：接下来，就请同学们按照刚刚探究出的解题思路，完成这道试题的解答.

简析：分析问题是解决问题的前提.教师从例题的隐性条件分析入手，围绕条件和结论展开综合分析，逐步引导学生发现问题解决的基本途径.通过若干个知识的简单串联，最终形成了完整的知识应用和问题解决的链接.

3.解法讲评

15分钟后，教师结合学生的部分过程进行解法讲评.

投影一名学生的部分解题过程（下称解法1），如图2.

图2

教师：这里为何不按照平常的“x1=…，x2=…”写解呢？

学生14：说不清谁是x1，谁是x2.

教师：那该怎么办呢？

学生15：对这两个解分类讨论！

教师：很好！怎么分？

教师：说得真好！在这两种情形下，我们该怎么解呢？（投影一名学生给出的完整、规范的过程，并进行简单点评）

教师：还有其他解法吗？

（投影学生的另外两种解法，这里只呈现不同解法部分的解题过程）

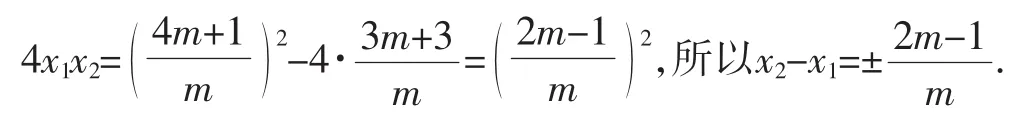
简析：解法讲评是复习教学的核心环节，在学生自主解答结束后，教师提出“为什么要分类”，“怎么分”，“怎么解”，“还有其他解法吗”等一系列问题，引导学生渐进呈现、积极展示，多样的解题过程不仅丰富了学生的求解思路，而且对学生的解法的优选与优化也是非常有利的.

4.总结提升

教师：在刚才的求解中我们用到了哪些知识？

学生16：求AB的解析式用的是“待定系数法”，求x1，x2用的是因式分解法.

学生17：解这个方程我用的是公式法.

学生18：我没有解方程，直接用根与系数的关系将n=x1-x2-2转化成只含有n、m的式子.

教师：看来，这道题目给出的方程是解题绕不开的“坎”，将方程中的条件转化到n=x1-x2-2中去，是我们解题的关键.这种转化思想在本题中得到了很好的应用，除此之外，本题中还用到了哪些数学思想呢？

学生19：分类讨论.

教师：对！与转化一样，分类讨论思想是初中的核心数学思想，在问题解决中有着非常广泛的应用.

学生20：还用到了函数思想和数形结合思想.

教师：对！我们从题中可以抽象出“n与m是一种函数关系”，点P（m，n）所形成的曲线正是这个函数的图像.

教师：非常棒！从这样一道小题中，我们挖掘出如此丰富的“思想内涵”，看来，我们的探索与交流是值得的！

简析：数学思想是数学留给学生最后的财富，是与学生后续学习生活息息相关的数学核心知识.因此，数学思想的教学也是初中数学教学的最重要的内容之一.为了让学生知晓这些核心知识的应用价值，教者引导学生回顾解题与交流过程，不仅梳理了用到的基础知识，还将所涉及的数学思想一并明晰.在例题教学的末端，这样的归纳总结是十分必要的.

三、三点思考

1.精选细磨，关注例题的质量

从上面的例题教学不难看出，“一题一课”对例题的要求还是很高的.首先，例题所蕴含的知识要是数学的核心知识（主干知识）；其次，知识的含量应该比较大，或者知识的延展性应该较强，能进行必要的拓展；还有，例题所包含的知识种类也应是多样的，既要有基础知识，又要有基本技能和基本数学思想.所以，我们应学会精挑细选，学会从众多的考题、经典试题中挑选出符合上述要求的题目出来.当然，对所选题目进行必要的打磨还是不可缺少的.例题打磨的主要任务是将选择的题目与课时目标进行关联，剔除无关的考点，增加核心考点，从而保证最终呈现出的例题具有很高的“含金量”.

2.合理设计，提升教学的效度

想要上好一节专题复习课，不仅要选择与打磨例题，还应对例题的教学过程进行精心设计.“一题一课”不能因为例题少而让某一应有环节缺失，为了达成“做一题，得一法，会一类，通一片”的目标，在中考二轮复习课上，我们一般以一道例题为载体，开展一次详实分析，组织一次独立练习，进行一次有效讲评，完成一次深度小结.整个教学过程，学生应是活动的主体，教师应以问题（组）引领学生展开探索与交流，努力将能力的形成建构在知识的梳理之上，通过知识的网络化推动学生问题解决能力的提升.所以，在形成教学例题后，应对教学例题进行精心设计，找出例题教学的最佳“切入点”，形成知能提升的适合“爆发点”，以实现例题教学效益的最大化.

3.指向核心，确保复习的方向

数学核心知识是学生问题解决应用最多的知识，也是教师在课堂教学中应高度关注的知识.这些知识不只是数学基础知识，还包括很多的隐性知识，比如一些重要的数学思想，以及那些来自于学生生活与学习的活动经验，这些都是潜移默化中影响着学生成长的知识.在课堂上，这些知识的出镜率应该是最高的，无论是学生的探索，还是全班的交流，抑或是教师的点评，都应以这些知识为话题，让它们真正走上前台，成为教学的主角.只有这样，我们才能让核心知识的价值落在实处，也只有这样，才能保证我们的复习方向准确，成效显著.